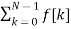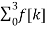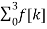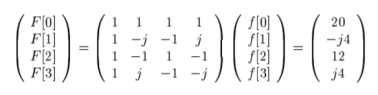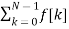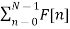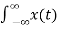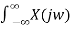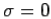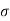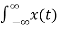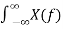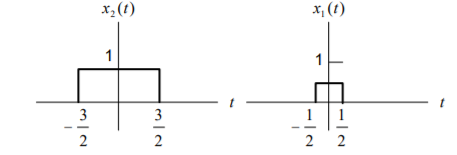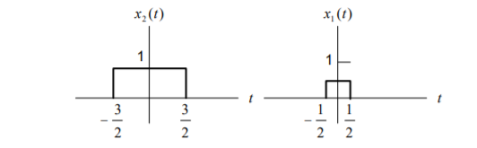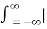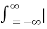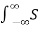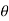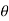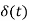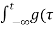A1) Let f(t) be the continuous signal which is the source of the data. Let N samples be denoted f[0],f[1],f[2],………..,f[k],…….,f[N-1].

The Fourier Transform of the original signal f(t) would be

F(jw) = e-jwt dt

Each sample f[k] as an impulse has area f[k]. Then since the integrand exists only at the sample points:

F(jw) = e -jwt dt

= f(0) e -j0 + f[1] e -jwT + …… + f[k] e -jwT + …. F(N-1) e -jw(N-1)T

That is F(jw) = e -jwkT

The continuous Fourier transform could be evaluated over a finite interval usually the fundamental period rather than from -∞ to ∞ . Similarly, since there are only a finite number of input data points, the DFT treats the data as if it were periodic form f(N) to f(2N-1).
Hence the sequence shown below in Figure (a) is one period of the periodic sequence in plot (b)

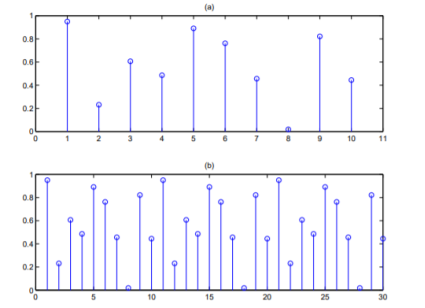
Figure.1 (a) Sequence of N=10 pts. (b) implicit periodicity in DFT

Since the operation treats the data as periodic, we evaluate the DFT equation for the fundamental frequency (one cycle per sequence, 1/NT Hz, 2π/NT rad/sec and its harmonics at w=0.

In general

F[n] = e -j2π/N nk                   (n=0:N-1)

F[n] is the Discrete Fourier Transform of the sequence f[k].

In matrix form we get

A2) F[n] =   e -j π/2 nk =   (-j) nk

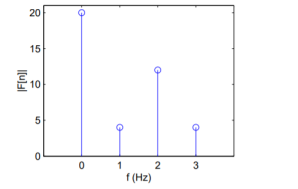
   Figure. Magnitude of the four point sequence.

The inverse transform of

F[n] =   e -j 2π/N nk

That is

f[k] = 1/N    e j 2π/N nk

A3) The Fourier transform pair in the most general form for a continuous and aperiodic time signal x(t) is (Eqs. 1 and 2 :

X(jw) = e -jwt dt

x(t) = 1/2π  e jwt dw

The spectrum X(jw)  is expressed as a function of jw because the spectrum can be treated as the Laplace transform of the signal X(s) evaluated along the imaginary axis ():
 

X(jw) = X(s) |s=jw                           in general s= + jw

However, in practice, it is more convenient to represent the frequency of a signal by f=w/2π in cycles/ second or Hertz (Hz, KHz, MHz, GHz, etc.), instead of w in radians/second. Replacing w by 2πf, we can also express the spectrum as X(j2πf)  or simply X(f) in this alternative representation:

X(f) = e -j2πft dt

x(t) = e j2πft df

A4)

Figure . Input signal

This signal can be obtained as a linear combination of

x(t) = ½ x1(t-2.5) + x2(t-2.5)

Figure . Combination of x1(t) and x2(t)

where x1(t) and x2(t) are rectangular pulse signals and their Fourier transforms are

X1(jw) = 2 sin (w/2) / w and X2(jw) = 2 sin (3w/2)/w

Using linearity and time shifting properties of Fourier transform yields

X(jw) = e -j5w/2 { sin(w/2) + 2 sin(3w/2) /w}

Figure . The output waveform

(i)                Linearity

If x(t)          F               X(jw)

y(t)          F               Y(jw)

Then

a x(t) + b y(t)           F            a X(jw) + b Y(jw)

(ii)             Time shifting

If x(t)          F               X(jw)

Then

x(t-to)       F              e -jwto X(jw)

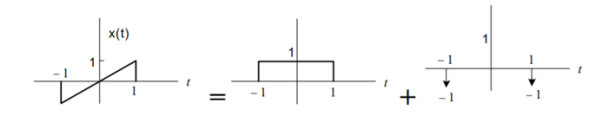
Figure . Input signal x(t) and its interpretation

From the above figure we see that g(t) = d x(t) /dt is a sum of rectangular pulse and two impulses.

G(jw) = (2 sin w/w) – e jw – e -jw

Using integration property we obtain

X(jw) = G(jw) / jw + π G(0) δ(w) = 2 sin w/ j w 2 – 2 cos w / jw

It can be found that X(jw) is purely imaginary and odd which is consistent with the fact that x(t) is real and odd.

A7)

If  x(t)       F            X(jw)

We have

x(t)| 2 dt = 1/ 2 π X(jw)| 2 dw

Parseval’s relation states that the total energy may be determined either by computing the energy per unit time |x(t)| 2 and integrating over all the time by computing the energy per unit frequency |X(jw)| 2  / 2 π and integrating over all frequencies.

For this reason |X(jw)|  is often referred to as energy-density spectrum.

A8)

y(t) = h(t) * x(t)               F             Y(jw) = H(jw) X(jw)

Multiplication property

r(t) = s(t) p(t)                            R(jw) = 1/2π (j) P(j(w-) d

Multiplication of one signal by another can be thought as one signal to scale or modulate the amplitude of the other consequently the multiplication of two signals is referred to as amplitude modulation.

A9) We know that

g(t) =                             1

Also note that

x(t) = ) dτ

The fourier transform of this function is

X(jw) = 1/jw + π G(0) δ(w) = 1/jw + π δ(w)

Where G(0) =1 .