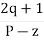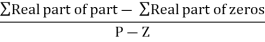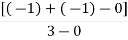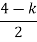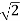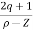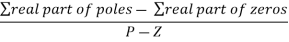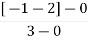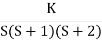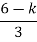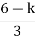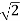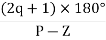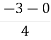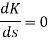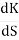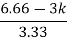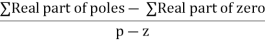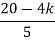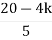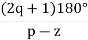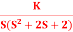undefined | unit 5 rootlocus techniques

Unit-5Root–Locus Techniques Q1) Sketch the root locus for given open loop transfer function G(S) =

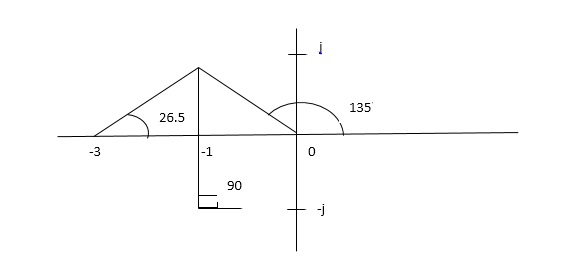
.A1) G(s) =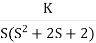

Number of Zeros = 0Number of polls S = (0, -1+j, -1-j) = (3).1) Number of Branches = max (P, Z) = max (3, 0) = 3.2) As there are no zeros in the system so, all branches terminate at infinity.3) As P>Z, branches terminate at infinity through the path shown by asymptotes

Asymptote = × 180° q = 0, 1, 2………..(p-z-1)

P=3, Z=0.

q= 0, 1, 2.

For q=0

Asymptote = 1/3 × 180° = 60°

For q=1

Asymptote = × 180°

= 180°

For q=2

Asymptote = × 180° = 300°

Asymptotes = 60°,180°,300°.

4) Asymptote intersects real axis at centroid

Centroid =

Centroid = -0.66

5) As poles are complex so angle of departure øD = (2q+1) × 180°+øø = ∠Z –∠P.Calculating ø for S=0

Join all the other poles with S=0ø = ∠Z –∠P.= 0-(315°+45°)= -360°ØD = (2q + 1)180 + ø.= 180° - 360°ØD = -180° (for q=0) = 180° (for q=1) =540° (for q=2) Calculation ØD for pole at (-1+j)

ø = ∠Z –∠P.= 0 –(135°+90°)= -225°ØD = (2q+1) 180°+ø.= 180-225°= -45°ØD = -45° (for q = 0) = 315° (for q = 1)= 675° (for q =2)6) The crossing point on imaginary axis can be calculated by Routh Hurwitz the characteristic equation is.1+G(s) H (s) = 01+

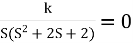S (S2+2s+2)+k = 0

S3+2s2+2s+K = 0

S3	1	1	0
S2	2	K	0
S1		0
S0	K

For stability

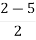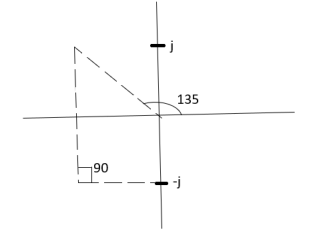
> 0. And K > 0.

0<K<2.

So, when K=2 root locus crosses imaginary axis

S3 + 2S2 + 2S + 2 =0

For k

Sn-1 = 0 n : no. of intersection

S2-1 = 0 at imaginary axis

S1 = 0

= 0

K<4

For Sn = 0 for valve of S at that K

S2 = 0

2S2 + K = 0

2S2 + 2 = 0

2(S2 +1) = 0

32 = -2

S = ± j

The root locus plot is shown in figure 1.

Fig 1 Root Locus for G(S) =

Q2) Sketch the root locus plot for the following open loop transfer functionG(s) =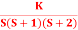

A2)

Number of zero = 0, number of poles = 3

As P>Z, branches will terminate at infinity

There are no zeros so all branches will terminate at infinity.

The path for the branches is shown by asymptote

Asymptote = ×180°. q=0,1,………p-z-1

P=3, Z=0

q= 0,1,2.

For q = 0

Asymptote = × 180° = 60.

For q=1

Asymptote = × 180° = 180°

For q=2

Asymptote = × 180° = 300°

5. Asymptote intersect real axis at centroid

Centroid =

= = -1

6. As root locus lies between poles S= 0, and S= -1

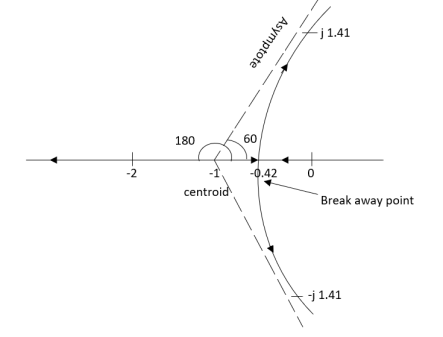
So, calculating breakaway point.

= 0

The characteristic equation is

1+ G(s) H (s) = 0.

1+ = 0

K = -(S3+3S2+2s)

= 3S2+6s+2 = 0

3s2+6s+2 = 0

S = -0.423, -1.577.

So, breakaway point is at S=-0.423

because root locus is between S= 0 and S= -1

7. The intersection of root locus with imaginary axis is given by Routh criterion.

Characteristics equation is

S3+3S3+2s+K = 0

S3	1	2
S2	3	K
S1		0
S0	K

For k

Sn-1= 0 n: no. of intersection with imaginary axis

n=2

S1 = 0

= 0

K < 6 Valve of S at the above valve of K

Sn = 0

S2 = 0

3S2 + K =0

3S2 +6 = 0

S2 + 2 = 0

S = ± j

Fig 2 Root Locus for G(s) =

The root locus plot is shown in fig. 2. Q3) Plot the root locus for the given open loop transfer function G(s) =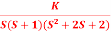

A3)

Number of zeros = 0 number of poles = 4

P = (S=0,-1,-1+j,-1-j) = 42. As P>Z all the branches will terminated at infinity.3. As no zeros so all branches terminate at infinity.4. The path for branches is shown by asymptote.

Asymptote = q = 0,1,…..(Þ-z-1)

q=0,1,2,3. (P-Z = 4-0)

for q=0

Asymptote = ×180° =45°

For q=1

Asymptote = ×180° =135°

For q=2

Asymptote = ×180° =225°

For q=3

Asymptote = ×180° =315°

5. Asymptote intersects real axis at unmarried

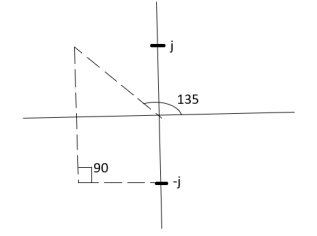
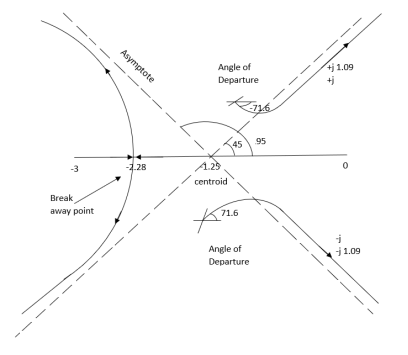
Centroid =

Centroid = = = -0.75

6) As poles are complex so angle of departure is

ØD = (2q+1) ×180 + ø ø = ∠Z –∠P.

A) Calculating Ø for S=0

ø = ∠Z –∠P.= 0 –[315° + 45°]Ø = -360°For q = 0ØD = (2q+1) 180° + Ø= 180 - 360°ØD = -180°b) Calculating Ø for S=-1+jø = ∠Z –∠P.= 0-[135° + 90° + 90°]Ø = -315°For q=0ØD= (2q+1) 180° +Ø= 180° -315°ØD = -135°ØD for S=1+j will be ØD = 45° 7) As the root locus lie between S=0 and S=-1

So, the breakaway point is calculated

1+ G(s)H(s) = 0

1+ = 0

(S2+S)(S2 +2S+2) + K =0

K = -[S4+S3+2s3+2s2+2s2+2s]

= 4S3+9S2+8S+2=0

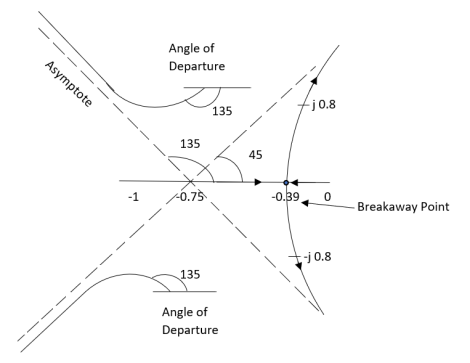
S = -0.39, -0.93, -0.93.

The breakaway point is at S = -0.39 as root locus exists between S= 0 and S=-18) Intersection of root locus with imaginary axis is given by Routh Hurwitz

I + G(s) H(s) = 0

K+S4+3S3+4S2+2S=0

S4	1	4	K
S3	3	2
S2	3.33	K
S1
S0	K

For system to be stable

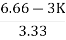>06.66>3K0<K<2.22.For K = 2.223.3352+K =03.3352 + 2.22 = 0S2 = -0.66S = ± j 0.816.The root locus plot is shown in figure 3.

Fig 3 Root Locus for G(s) =

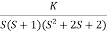Q4) Plot the root locus for open loop systemG(s) =

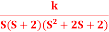A4)1) Number of zero = 0 number of poles = 4 located at S=0, -2, -1+j, -1-j.2) As no zeros are present so all branches terminated at infinity.3) As P>Z, the path for branches is shown by asymptoteAsymptote =

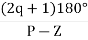q = 0,1,2……p-z-1For q = 0Asymptote = 45°q=1Asymptote = 135°q=2Asymptote = 225°q=3Asymptote = 315°4) Asymptote intersects real axis at centroid.

Centroid =

Centroid = -1.

5) As poles are complex so angle of departure isØD=(2q+1)180° + Ø ø = ∠Z –∠P = 0-[135°+45°+90°]= 180°- 270°ØD = -90°6) As root locus lies between two poles so calculating point. The characteristic equation is 1+ G(s)H(s) = 01+

= 0. K = -[S4+2S3+2S2+2S3+4S2+4S]K = -[S4+4S3+6S2+4S]

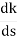= 0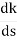

= 4s3+12s2+12s+4=0S = -1So, breakaway point is at S = -17) Intersection of root locus with imaginary axis is given by Routh Hurwitz.

S4+4S3+6S2+4s+K = 0

S4	1	6	K
S3	4	4
S2	5	K
S1
S0	K

≤ 0

K≤5.For K=5 valve of S will be.5S2+K = 05S2+5 = 0 S2 +1 = 0S2 = -1S = ±j.The root locus is shown in figure 4.

Fig 4 Root Locus For G(s) =

Q5) Plot the root locus for open loop transfer function G(s) =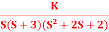

A5)

Number of zeros = 0. Number of poles = 4 located at S=0, -3, -1+j, -1-j.

As no. zero so all branches terminate at infinity.

The asymptote shows the both to the branches terminating at infinity.

Asymptote = q=0,1,….(p-z).

For q = 0

Asymptote = 45

For q = 1

Asymptote = 135

For q = 2

Asymptote = 225

For q = 3

Asymptote = 315

(4). The asymptote intersects real axis at centroid.

Centroid = ∑Real part of poles - ∑Real part of zero / P – Z

= [-3-1-1] – 0 / 4 – 0

Centroid = -1.25

(5). As poles are complex so angle of departureφD = (29 + 1)180 + φ

ø = ∠Z –∠P.= 0 – [ 135 + 26.5 + 90 ]= -251.56For q = 0φD = (29 + 1)180 + φ= 180 – 215.5φD = - 71.56(6). Break away point dk / ds = 0 is at S = -2.28.(7). The intersection of root locus on imaginary axis is given by Routh Hurwitz.1 + G(S)H(S) = 0K + S4 + 3S3 + 2S3 + 6S2 + 2S2 + 6S = 0S4 1 8 KS3 5 6S2 34/5 KS1 40.8 – 5K/6.8K ≤ 8.16For K = 8.16 value of S will be6.8 S2 + K = 0 6.8 S2 + 8.16 = 0S2 = - 1.2S = ± j1.09The plot is shown in figure 20.

Fig 5 Root Locus for G(s) =

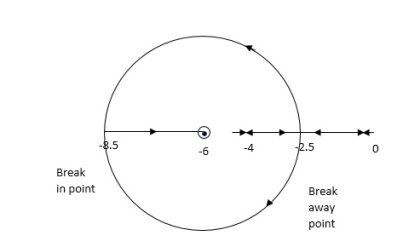
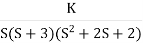Q6) Sketch the root locus for open loop transfer function. G(S) = K(S + 6)/S(S + 4)A6)

Number of zeros = 1(S = -6)

Number of poles = 2(S = 0, -4)2. As P > Z one branch will terminate at infinity and the other at S = -6.3. For Break away and breaking point 1 + G(S)H(S) = 01 + K(S + 6)/S(S + 4) = 0dk/ds = 0S2 + 12S + 24 = 0S = -9.5, -2.5 Breakaway point is at -2.5 and Break in point is at -9.5.4. Root locus will be in the form of a circle. So finding the centre and radius.

5. Let S =  + jw.

G( + jw) = K( + jw + 6)/(  + jw)(  + jw + 4 ) = +- π

tan-1 w/  + 6 - tan-1 w/  – tan-1 w /  + 4 = - π

taking tan of both sides.

w/  + w/  + 4 / 1 – w/  w/  + 4 = tan π + w /  + 6 / 1 - tan π w/  + 6

w/  + w/  + 4 = w/  + 6[ 1 – w2 /  ( + 4) ]

(2 + 4)(  + 6) = (2 + 4  – w2)

2 2 + 12 + 4 + 24 = 2 + 4 – w2

22 + 12 + 24 = 2 – w2

2 + 12 – w2 + 24 = 0

Adding 36 on both sides

( + 6)2 + (w + 0)2 = 12

The above equation shows circle with radius 3.46 and centre (-6, 0) the plot is shown in figure 6

Fig 6 Root locus for G(S) = K (S + 6)/S (S + 4)

Sign Up