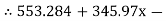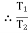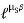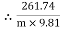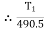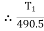ECEM
UNIT-2EQUILIBRIUM OF FORCES Q1) Determine the horizontal force P needed to just start moving the 300 N create up the plane as shown in figure. Take  = 0%A1) for the equilibrium
= 0%A1) for the equilibrium
 = 0
= 0 P – RNcos 70 – FScos 20 = 0
P – RNcos 70 – FScos 20 = 0 P – RNcos 70 –
P – RNcos 70 –  s FScos 20 = 0
s FScos 20 = 0 P – 0.342 RN 0.094 RN = 0
P – 0.342 RN 0.094 RN = 0 P = 0.436 RN
P = 0.436 RN
 – 300 + RN Sin 70 – FS Sin 20 = 0
– 300 + RN Sin 70 – FS Sin 20 = 0 – 300 + RN Sin 70 –
– 300 + RN Sin 70 – 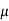 s FS Sin 20 = 0
s FS Sin 20 = 0 – 300 + RN Sin 70 – 0.1 RN Sin 20 = 0
– 300 + RN Sin 70 – 0.1 RN Sin 20 = 0 – 300 + 0.94 RN – 0.342 RN = 0
– 300 + 0.94 RN – 0.342 RN = 0 0.9058 RN = 300
0.9058 RN = 300 RN = 331.2 N
RN = 331.2 N n 1P = 0.436
n 1P = 0.436  331.2P = 144.4 N ------------------- force required Q2) A body of weight 50 N is along rough horizontal plane A pull of 18 N acting at an angle of 140 with the horizontal find coefficient of static friction. A2)Considering the equilibrium of block
331.2P = 144.4 N ------------------- force required Q2) A body of weight 50 N is along rough horizontal plane A pull of 18 N acting at an angle of 140 with the horizontal find coefficient of static friction. A2)Considering the equilibrium of block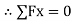
 18 Cos 14 – Fs = 0
18 Cos 14 – Fs = 0 Fs = 17.46 N
Fs = 17.46 N 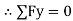 RN + 18 Sin 14 – 50 = 0RN = 45.64 NAs Fs =
RN + 18 Sin 14 – 50 = 0RN = 45.64 NAs Fs =  S RN17.46 =
S RN17.46 =  S
S 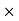 45.64
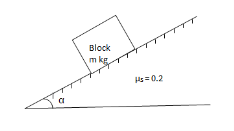
45.64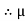 S = 0.386 Q3) A block of mass m rests on frictional plane which makes an angle
S = 0.386 Q3) A block of mass m rests on frictional plane which makes an angle  with horizontal as shown if the coefficient Of friction between the block & frictional plane is 0.2, determine angle
with horizontal as shown if the coefficient Of friction between the block & frictional plane is 0.2, determine angle  for limiting friction
for limiting friction
A3) For limiting frictionTan  tan
tan  S =
S =  S
S tan-1
tan-1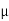 S
S tan-1
tan-1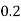
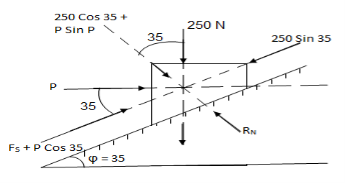
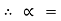 11.310Q4) Determine whether the block shown is in equilibrium and find the magnitude and direction of friction force when
11.310Q4) Determine whether the block shown is in equilibrium and find the magnitude and direction of friction force when  = 350 and P = 100 N.
= 350 and P = 100 N.
A4) let us select inclined plane as x-x axis & perpendicular to plane as y-y axisLet Fs = static frictional force which is required to maintain equilibrium. Resolving force along x-axis
Resolving force along x-axis Fs + 100 Cos 35 – 250 Sin 35 = 0
Fs + 100 Cos 35 – 250 Sin 35 = 0 Fs – 61.48 = 0
Fs – 61.48 = 0 Fs = 61.48 N ----- frictional force
Fs = 61.48 N ----- frictional force 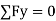 --resolving force along y-axis
--resolving force along y-axis -(250 Cos 35 + P Sin 35) + RN = 0
-(250 Cos 35 + P Sin 35) + RN = 0 -250 Cos 35 – 100 Sin 35 + RN = 0-262.15 + RN = 0
-250 Cos 35 – 100 Sin 35 + RN = 0-262.15 + RN = 0 RN = 262.15 N -------- normal reaction Maximum frictional force can be developed is given byFs max =
RN = 262.15 N -------- normal reaction Maximum frictional force can be developed is given byFs max =  S
S RN = 0.3
RN = 0.3 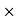 262.15Fs max = 78.65 N As frictional force required maintaining equilibrium (61.48 N) is less than max. Frictional force,
262.15Fs max = 78.65 N As frictional force required maintaining equilibrium (61.48 N) is less than max. Frictional force, Equilibrium will be maintained Q5) Uniform ladder AB has a length of 8 m and mass 24kg end A is on horizontal floor end B rests against vertical wall. A man of mass of 60 kg has to climb this ladder. At what position from the base will be induce the slipping of ladder
Equilibrium will be maintained Q5) Uniform ladder AB has a length of 8 m and mass 24kg end A is on horizontal floor end B rests against vertical wall. A man of mass of 60 kg has to climb this ladder. At what position from the base will be induce the slipping of ladder
A5)Take S = 0.34 at all contact surface.Weight of man = 60
S = 0.34 at all contact surface.Weight of man = 60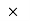 9.81 =588.6 NWeight of ladder
9.81 =588.6 NWeight of ladder  AB = 8 mImpending motion
AB = 8 mImpending motion Ac = 8 Cos 54
Ac = 8 Cos 54 BC = 8 Sin 54
BC = 8 Sin 54 ɑ = 2.35 m
ɑ = 2.35 m b = x Cos 54
b = x Cos 54 FSA =
FSA = 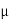 S
S  RNA
RNA  FSB =
FSB = 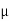 S
S 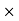 RNB Considering the equilibrium of ladder
RNB Considering the equilibrium of ladder FX = 0
FX = 0
Taking moment about point A, MA = 0
MA = 0
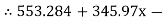 1.598 RNB – 6.47 RNB = 0
1.598 RNB – 6.47 RNB = 0 345.97x – 8.068 RNB = 553.284
345.97x – 8.068 RNB = 553.284 345.97x – 8.068
345.97x – 8.068  251.14 = 553.284
251.14 = 553.284 345.97x = 1472.913X = 4.257 mAns :At X = 4.257 m from point A, along the ladder, man can climb without slipping. Beyond this distance, ladder will be slipping. Q6) A 137 kg block is supported by a rope which Is wrapped 1.5 times around a horizontal Rod knowing that coefficientOf static friction Between rope and rod is 0.15, determine The range of values of P for which Equilibrium is maintained. A6)Weight of block =
345.97x = 1472.913X = 4.257 mAns :At X = 4.257 m from point A, along the ladder, man can climb without slipping. Beyond this distance, ladder will be slipping. Q6) A 137 kg block is supported by a rope which Is wrapped 1.5 times around a horizontal Rod knowing that coefficientOf static friction Between rope and rod is 0.15, determine The range of values of P for which Equilibrium is maintained. A6)Weight of block = 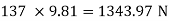 Angle of contact = LAP Angle
Angle of contact = LAP Angle
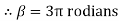 A) Case I : when P > 1343.97 NForce P tends to move the rope down ward and block moves upward. Thus the part rope on which force P is acting is height side and rope to which block is attached is slack side.
A) Case I : when P > 1343.97 NForce P tends to move the rope down ward and block moves upward. Thus the part rope on which force P is acting is height side and rope to which block is attached is slack side. =
= 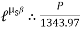 =
= 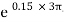
 P = 5525.34 NB) Case II : when P < 1343.97 N
P = 5525.34 NB) Case II : when P < 1343.97 N force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward.
force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward. Rope side to which block is attached is tight side and another side is slack side.
Rope side to which block is attached is tight side and another side is slack side.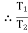 =
= 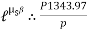 =
= 
 P = 326.92 N
P = 326.92 N Range of P for equilibrium is 326.92 N
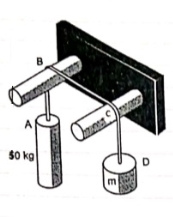
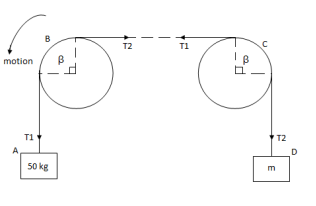
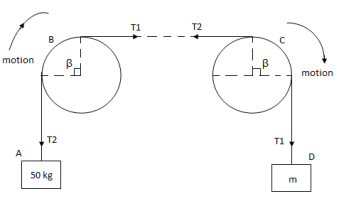
Range of P for equilibrium is 326.92 N 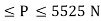 Q7) two cylinders are connected by a rope that passes over two fixed rods as shown. Knowing that the Coefficient of static friction between the rope and the rods is 0.40, determine the range of the mass m Of cylinder D for which equilibrium is maintained. A7) Weight of cylinder = 50
Q7) two cylinders are connected by a rope that passes over two fixed rods as shown. Knowing that the Coefficient of static friction between the rope and the rods is 0.40, determine the range of the mass m Of cylinder D for which equilibrium is maintained. A7) Weight of cylinder = 50  9.81 = 490.5 N
9.81 = 490.5 N
Lap angle = 
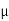 S = 0.40A) Case I :Weight of cylinder A > weight of cylinder B
S = 0.40A) Case I :Weight of cylinder A > weight of cylinder B
In this case cylinder A will tends to move downward while B will tends to move upwardConsider part AB of the Rope as AB rope is moving down,Tension in hight side T1 =  Tension in slack side = T2 = unknown.
Tension in slack side = T2 = unknown.  =
=  =
=  = 1.874
= 1.874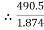 = T2
= T2 T2 = 261.74 N Consider part CD, of the rope. As rope CD is moving upward,Tension in tight side T1 = T2 of rope ABTension in tight side, T1 = 261.74 NTension in slack side = T2 = (m
T2 = 261.74 N Consider part CD, of the rope. As rope CD is moving upward,Tension in tight side T1 = T2 of rope ABTension in tight side, T1 = 261.74 NTension in slack side = T2 = (m  9.81)
9.81)
B) Case II :Weight of cylinder A < weight of cylinder B
In this case cylinder a will tends to move upward while cylinder B will tends to move downwardConsider part AB of the rope moving upwardsTension in slack side = side A = 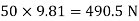
Consider part CD of rope, Rope CD is moving downwardsTension in tight side = T1 = (m 9.81) NTension in slack side = T2 = T1 of rope AB = 919.197 N
9.81) NTension in slack side = T2 = T1 of rope AB = 919.197 N
Range of mass m for equilibrium to be maintained is14.23 kg  m
m 175.59 kg Q8) A Force P = mg/6 is required to lower the cylinder with card making 1.25 turns around the fixed shaft. Determine the coefficientOf friction “
175.59 kg Q8) A Force P = mg/6 is required to lower the cylinder with card making 1.25 turns around the fixed shaft. Determine the coefficientOf friction “ S” between the card and the shaftRefer the figure
S” between the card and the shaftRefer the figure  A8)
A8)
Lap angle = 2.5
= 2.5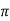 radians For flat belt,
radians For flat belt, =
= 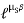
 =
= 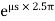
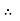 6
6 
 1.79 =
1.79 = 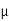 S
S 2.5
2.5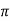
 S = 0.23 Q9) Determine the range of P for the equilibrium of block of weight W as shown in fig. the coefficientOf friction between rope and pulley is 0.2 A9)
S = 0.23 Q9) Determine the range of P for the equilibrium of block of weight W as shown in fig. the coefficientOf friction between rope and pulley is 0.2 A9)
Case I : when P is max. =
= 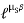
 =
= 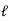
 Pmax = 1.369 wCase II : when P is min.
Pmax = 1.369 wCase II : when P is min. =
= 

 Pmin = 0.73 wFor equilibrium P must be between 0.73
Pmin = 0.73 wFor equilibrium P must be between 0.73  P
P  1.369 w Q10) Explain type of friction?A10) Types of frictionFriction is the force that opposes motion between any surfaces that are in contact. There are four types of friction: static, sliding, rolling, and fluid friction. Static, sliding, and rolling friction occur between solid surfaces. Fluid friction occurs in liquids and gases. All four types of friction are described below.Static FrictionStatic friction acts on objects when they are resting on a surface. For example, if you are hiking in the woods, there is static friction between your shoes and the trail each time you put down your foot (see Figure below). Without this static friction, your feet would slip out from under you, making it difficult to walk. In fact, that's exactly what happens if you try to walk on ice. That's because ice is very slippery and offers very little friction.Sliding FrictionSliding friction is friction that acts on objects when they are sliding over a surface. Sliding friction is weaker than static friction. That's why it's easier to slide a piece of furniture over the floor after you start it moving than it is to get it moving in the first place. Sliding friction can be useful. For example, you use sliding friction when you write with a pencil. The pencil “lead” slides easily over the paper, but there's just enough friction between the pencil and paper to leave a mark.Rolling FrictionRolling friction is friction that acts on objects when they are rolling over a surface. Rolling friction is much weaker than sliding friction or static friction. This explains why most forms of ground transportation use wheels, including bicycles, cars, 4-wheelers, roller skates, scooters, and skateboards. Ball bearings are another use of rolling friction. You can see what they look like in the Figure below. They let parts of a wheel or other machine roll rather than slide over on another.
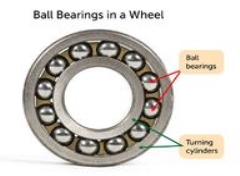
1.369 w Q10) Explain type of friction?A10) Types of frictionFriction is the force that opposes motion between any surfaces that are in contact. There are four types of friction: static, sliding, rolling, and fluid friction. Static, sliding, and rolling friction occur between solid surfaces. Fluid friction occurs in liquids and gases. All four types of friction are described below.Static FrictionStatic friction acts on objects when they are resting on a surface. For example, if you are hiking in the woods, there is static friction between your shoes and the trail each time you put down your foot (see Figure below). Without this static friction, your feet would slip out from under you, making it difficult to walk. In fact, that's exactly what happens if you try to walk on ice. That's because ice is very slippery and offers very little friction.Sliding FrictionSliding friction is friction that acts on objects when they are sliding over a surface. Sliding friction is weaker than static friction. That's why it's easier to slide a piece of furniture over the floor after you start it moving than it is to get it moving in the first place. Sliding friction can be useful. For example, you use sliding friction when you write with a pencil. The pencil “lead” slides easily over the paper, but there's just enough friction between the pencil and paper to leave a mark.Rolling FrictionRolling friction is friction that acts on objects when they are rolling over a surface. Rolling friction is much weaker than sliding friction or static friction. This explains why most forms of ground transportation use wheels, including bicycles, cars, 4-wheelers, roller skates, scooters, and skateboards. Ball bearings are another use of rolling friction. You can see what they look like in the Figure below. They let parts of a wheel or other machine roll rather than slide over on another.
The ball bearings in this wheel reduce friction between the inner and outer cylinders when they turn.[Figure3]Fluid FrictionFluid friction is friction that acts on objects that are moving through a fluid. A fluid is a substance that can flow and take the shape of its container. Fluids include liquids and gases. If you've ever tried to push your open hand through the water in a tub or pool, then you've experienced fluid friction. You can feel the resistance of the water against your hand. Look at the skydiver in the Figure below. He's falling toward Earth with a parachute. Resistance of the air against the parachute slows his descent. The faster or larger a moving object is, the greater is the fluid friction resisting its motion. That's why there is greater air resistance against the parachute than the skydiver's body.
 = 0%A1) for the equilibrium
= 0%A1) for the equilibrium
|
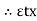 = 0
= 0 P – RNcos 70 – FScos 20 = 0
P – RNcos 70 – FScos 20 = 0 P – RNcos 70 –
P – RNcos 70 –  s FScos 20 = 0
s FScos 20 = 0 P – 0.342 RN 0.094 RN = 0
P – 0.342 RN 0.094 RN = 0 P = 0.436 RN
P = 0.436 RN
 – 300 + RN Sin 70 – FS Sin 20 = 0
– 300 + RN Sin 70 – FS Sin 20 = 0 – 300 + RN Sin 70 –
– 300 + RN Sin 70 – 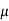 s FS Sin 20 = 0
s FS Sin 20 = 0 – 300 + RN Sin 70 – 0.1 RN Sin 20 = 0
– 300 + RN Sin 70 – 0.1 RN Sin 20 = 0 – 300 + 0.94 RN – 0.342 RN = 0
– 300 + 0.94 RN – 0.342 RN = 0 0.9058 RN = 300
0.9058 RN = 300 RN = 331.2 N
RN = 331.2 N n 1P = 0.436
n 1P = 0.436  331.2P = 144.4 N ------------------- force required Q2) A body of weight 50 N is along rough horizontal plane A pull of 18 N acting at an angle of 140 with the horizontal find coefficient of static friction. A2)Considering the equilibrium of block
331.2P = 144.4 N ------------------- force required Q2) A body of weight 50 N is along rough horizontal plane A pull of 18 N acting at an angle of 140 with the horizontal find coefficient of static friction. A2)Considering the equilibrium of block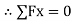
 18 Cos 14 – Fs = 0
18 Cos 14 – Fs = 0 Fs = 17.46 N
Fs = 17.46 N 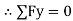 RN + 18 Sin 14 – 50 = 0RN = 45.64 NAs Fs =
RN + 18 Sin 14 – 50 = 0RN = 45.64 NAs Fs =  S RN17.46 =
S RN17.46 =  S
S 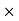 45.64
45.64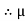 S = 0.386 Q3) A block of mass m rests on frictional plane which makes an angle
S = 0.386 Q3) A block of mass m rests on frictional plane which makes an angle  with horizontal as shown if the coefficient Of friction between the block & frictional plane is 0.2, determine angle
with horizontal as shown if the coefficient Of friction between the block & frictional plane is 0.2, determine angle  for limiting friction
for limiting friction
|
 tan
tan  S =
S =  S
S tan-1
tan-1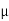 S
S tan-1
tan-1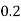
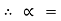 11.310Q4) Determine whether the block shown is in equilibrium and find the magnitude and direction of friction force when
11.310Q4) Determine whether the block shown is in equilibrium and find the magnitude and direction of friction force when  = 350 and P = 100 N.
= 350 and P = 100 N.
|
 Resolving force along x-axis
Resolving force along x-axis Fs + 100 Cos 35 – 250 Sin 35 = 0
Fs + 100 Cos 35 – 250 Sin 35 = 0 Fs – 61.48 = 0
Fs – 61.48 = 0 Fs = 61.48 N ----- frictional force
Fs = 61.48 N ----- frictional force 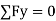 --resolving force along y-axis
--resolving force along y-axis -(250 Cos 35 + P Sin 35) + RN = 0
-(250 Cos 35 + P Sin 35) + RN = 0 -250 Cos 35 – 100 Sin 35 + RN = 0-262.15 + RN = 0
-250 Cos 35 – 100 Sin 35 + RN = 0-262.15 + RN = 0 RN = 262.15 N -------- normal reaction Maximum frictional force can be developed is given byFs max =
RN = 262.15 N -------- normal reaction Maximum frictional force can be developed is given byFs max =  S
S RN = 0.3
RN = 0.3 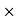 262.15Fs max = 78.65 N As frictional force required maintaining equilibrium (61.48 N) is less than max. Frictional force,
262.15Fs max = 78.65 N As frictional force required maintaining equilibrium (61.48 N) is less than max. Frictional force, Equilibrium will be maintained Q5) Uniform ladder AB has a length of 8 m and mass 24kg end A is on horizontal floor end B rests against vertical wall. A man of mass of 60 kg has to climb this ladder. At what position from the base will be induce the slipping of ladder
Equilibrium will be maintained Q5) Uniform ladder AB has a length of 8 m and mass 24kg end A is on horizontal floor end B rests against vertical wall. A man of mass of 60 kg has to climb this ladder. At what position from the base will be induce the slipping of ladderA5)Take
 S = 0.34 at all contact surface.Weight of man = 60
S = 0.34 at all contact surface.Weight of man = 60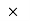 9.81 =588.6 NWeight of ladder
9.81 =588.6 NWeight of ladder  AB = 8 mImpending motion
AB = 8 mImpending motion Ac = 8 Cos 54
Ac = 8 Cos 54 BC = 8 Sin 54
BC = 8 Sin 54 ɑ = 2.35 m
ɑ = 2.35 m b = x Cos 54
b = x Cos 54 FSA =
FSA = 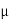 S
S  RNA
RNA  FSB =
FSB = 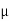 S
S 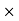 RNB Considering the equilibrium of ladder
RNB Considering the equilibrium of ladder FX = 0
FX = 0
|
From eqn…..1
RNB = 0.34
|
 MA = 0
MA = 0
|
|
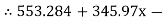 1.598 RNB – 6.47 RNB = 0
1.598 RNB – 6.47 RNB = 0 345.97x – 8.068 RNB = 553.284
345.97x – 8.068 RNB = 553.284 345.97x – 8.068
345.97x – 8.068  251.14 = 553.284
251.14 = 553.284 345.97x = 1472.913X = 4.257 mAns :At X = 4.257 m from point A, along the ladder, man can climb without slipping. Beyond this distance, ladder will be slipping. Q6) A 137 kg block is supported by a rope which Is wrapped 1.5 times around a horizontal Rod knowing that coefficientOf static friction Between rope and rod is 0.15, determine The range of values of P for which Equilibrium is maintained. A6)Weight of block =
345.97x = 1472.913X = 4.257 mAns :At X = 4.257 m from point A, along the ladder, man can climb without slipping. Beyond this distance, ladder will be slipping. Q6) A 137 kg block is supported by a rope which Is wrapped 1.5 times around a horizontal Rod knowing that coefficientOf static friction Between rope and rod is 0.15, determine The range of values of P for which Equilibrium is maintained. A6)Weight of block = 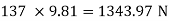 Angle of contact = LAP Angle
Angle of contact = LAP Angle
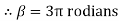 A) Case I : when P > 1343.97 NForce P tends to move the rope down ward and block moves upward. Thus the part rope on which force P is acting is height side and rope to which block is attached is slack side.
A) Case I : when P > 1343.97 NForce P tends to move the rope down ward and block moves upward. Thus the part rope on which force P is acting is height side and rope to which block is attached is slack side. =
= 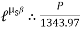 =
= 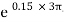
 P = 5525.34 NB) Case II : when P < 1343.97 N
P = 5525.34 NB) Case II : when P < 1343.97 N force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward.
force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward. Rope side to which block is attached is tight side and another side is slack side.
Rope side to which block is attached is tight side and another side is slack side.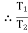 =
= 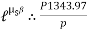 =
= 
 P = 326.92 N
P = 326.92 N Range of P for equilibrium is 326.92 N
Range of P for equilibrium is 326.92 N 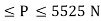 Q7) two cylinders are connected by a rope that passes over two fixed rods as shown. Knowing that the Coefficient of static friction between the rope and the rods is 0.40, determine the range of the mass m Of cylinder D for which equilibrium is maintained. A7) Weight of cylinder = 50
Q7) two cylinders are connected by a rope that passes over two fixed rods as shown. Knowing that the Coefficient of static friction between the rope and the rods is 0.40, determine the range of the mass m Of cylinder D for which equilibrium is maintained. A7) Weight of cylinder = 50  9.81 = 490.5 N
9.81 = 490.5 N
|

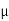 S = 0.40A) Case I :Weight of cylinder A > weight of cylinder B
S = 0.40A) Case I :Weight of cylinder A > weight of cylinder B
|
 Tension in slack side = T2 = unknown.
Tension in slack side = T2 = unknown.  =
=  =
=  = 1.874
= 1.874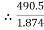 = T2
= T2 T2 = 261.74 N Consider part CD, of the rope. As rope CD is moving upward,Tension in tight side T1 = T2 of rope ABTension in tight side, T1 = 261.74 NTension in slack side = T2 = (m
T2 = 261.74 N Consider part CD, of the rope. As rope CD is moving upward,Tension in tight side T1 = T2 of rope ABTension in tight side, T1 = 261.74 NTension in slack side = T2 = (m  9.81)
9.81)
|
|
|
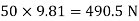
|
|
 9.81) NTension in slack side = T2 = T1 of rope AB = 919.197 N
9.81) NTension in slack side = T2 = T1 of rope AB = 919.197 N
|
|
 m
m 175.59 kg Q8) A Force P = mg/6 is required to lower the cylinder with card making 1.25 turns around the fixed shaft. Determine the coefficientOf friction “
175.59 kg Q8) A Force P = mg/6 is required to lower the cylinder with card making 1.25 turns around the fixed shaft. Determine the coefficientOf friction “ S” between the card and the shaftRefer the figure
S” between the card and the shaftRefer the figure  A8)
A8)
|
 = 2.5
= 2.5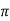 radians For flat belt,
radians For flat belt, =
= 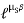
 =
= 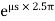
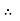 6
6 
 1.79 =
1.79 = 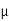 S
S 2.5
2.5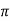
 S = 0.23 Q9) Determine the range of P for the equilibrium of block of weight W as shown in fig. the coefficientOf friction between rope and pulley is 0.2 A9)
S = 0.23 Q9) Determine the range of P for the equilibrium of block of weight W as shown in fig. the coefficientOf friction between rope and pulley is 0.2 A9)
|
 =
= 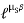
 =
= 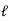
 Pmax = 1.369 wCase II : when P is min.
Pmax = 1.369 wCase II : when P is min. =
= 

 Pmin = 0.73 wFor equilibrium P must be between 0.73
Pmin = 0.73 wFor equilibrium P must be between 0.73  P
P  1.369 w Q10) Explain type of friction?A10) Types of frictionFriction is the force that opposes motion between any surfaces that are in contact. There are four types of friction: static, sliding, rolling, and fluid friction. Static, sliding, and rolling friction occur between solid surfaces. Fluid friction occurs in liquids and gases. All four types of friction are described below.Static FrictionStatic friction acts on objects when they are resting on a surface. For example, if you are hiking in the woods, there is static friction between your shoes and the trail each time you put down your foot (see Figure below). Without this static friction, your feet would slip out from under you, making it difficult to walk. In fact, that's exactly what happens if you try to walk on ice. That's because ice is very slippery and offers very little friction.Sliding FrictionSliding friction is friction that acts on objects when they are sliding over a surface. Sliding friction is weaker than static friction. That's why it's easier to slide a piece of furniture over the floor after you start it moving than it is to get it moving in the first place. Sliding friction can be useful. For example, you use sliding friction when you write with a pencil. The pencil “lead” slides easily over the paper, but there's just enough friction between the pencil and paper to leave a mark.Rolling FrictionRolling friction is friction that acts on objects when they are rolling over a surface. Rolling friction is much weaker than sliding friction or static friction. This explains why most forms of ground transportation use wheels, including bicycles, cars, 4-wheelers, roller skates, scooters, and skateboards. Ball bearings are another use of rolling friction. You can see what they look like in the Figure below. They let parts of a wheel or other machine roll rather than slide over on another.
1.369 w Q10) Explain type of friction?A10) Types of frictionFriction is the force that opposes motion between any surfaces that are in contact. There are four types of friction: static, sliding, rolling, and fluid friction. Static, sliding, and rolling friction occur between solid surfaces. Fluid friction occurs in liquids and gases. All four types of friction are described below.Static FrictionStatic friction acts on objects when they are resting on a surface. For example, if you are hiking in the woods, there is static friction between your shoes and the trail each time you put down your foot (see Figure below). Without this static friction, your feet would slip out from under you, making it difficult to walk. In fact, that's exactly what happens if you try to walk on ice. That's because ice is very slippery and offers very little friction.Sliding FrictionSliding friction is friction that acts on objects when they are sliding over a surface. Sliding friction is weaker than static friction. That's why it's easier to slide a piece of furniture over the floor after you start it moving than it is to get it moving in the first place. Sliding friction can be useful. For example, you use sliding friction when you write with a pencil. The pencil “lead” slides easily over the paper, but there's just enough friction between the pencil and paper to leave a mark.Rolling FrictionRolling friction is friction that acts on objects when they are rolling over a surface. Rolling friction is much weaker than sliding friction or static friction. This explains why most forms of ground transportation use wheels, including bicycles, cars, 4-wheelers, roller skates, scooters, and skateboards. Ball bearings are another use of rolling friction. You can see what they look like in the Figure below. They let parts of a wheel or other machine roll rather than slide over on another.
|
0 matching results found