Module-3
Integral Calculus
Question-1: Evaluate 
Sol. Let us suppose the integral is I,
I = 
Put c = 1 – x in I, we get
I = 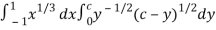
Suppose, y = ct
Then dy = c
Now we get,
I = 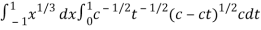
I = 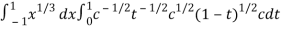
I = 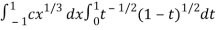
I = 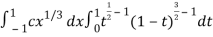
I =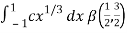
As we know that by beta function,
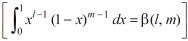
Which gives,
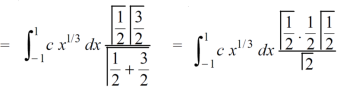
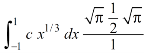
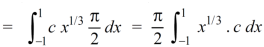
Now put the value of c, we get
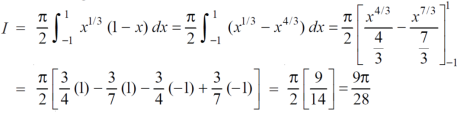
Question-2: Evaluate the following by changing to polar coordinates,
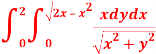
Sol. In this problem, the limits for y are 0 to  and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cosθ
r = 2 cosθ
From the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cosθ and y by r sinθ, dy dx by r drdθ,
We get,
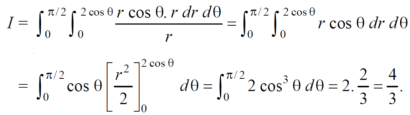
Question-3: Evaluate
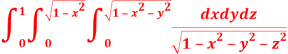
Solution:
Let
I = 
= 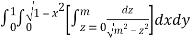
(Assuming m =  )
)
=  dxdy
dxdy
= 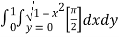
=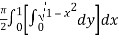
=  dx
dx
= 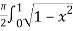 dx
dx
= 
=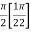
I =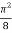
Question-4: Change the order of integration in the double integral-
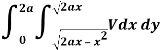
Sol.
Limits are given-
x = 0, x = 2a

And
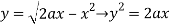
And
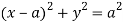
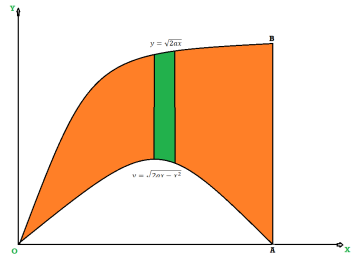
The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,
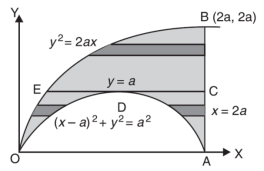
Now-
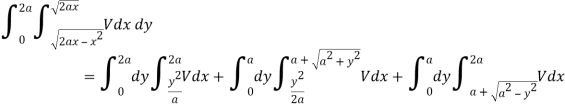
Which is the required answer.
Question-5: Change the order of integration for the integral  and evaluate the same with reversed order of integration.
and evaluate the same with reversed order of integration.
Sol:
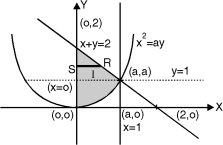 Given, I =
Given, I =  …(1)
…(1)
In the given integration, limits are
y= , y = 2a – x and x = 0, x = a
, y = 2a – x and x = 0, x = a
The region bounded by x2 = ay, x + y = 2a Fig.6.5
And x = 0, x = a is as shown in Fig. 6.5
Here we have to change order of Integration. Given the strip is vertical.
Now take horizontal strip SR.
To take total region, Divide region into two parts by taking line y = a.
1 st Region:
Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIelto x-axis therefore y varies from y = a to y = 2a.
 =dyxy dx.....…(2)
=dyxy dx.....…(2)
2nd Region:
Along strip, y constant and x varies from x = 0 to x= . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
 =dyxy dx…(3)
=dyxy dx…(3)
From Equation (1), (2) and (3),
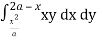 = dyxy dx + dyxy dx
= dyxy dx + dyxy dx
=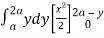 + y dy
+ y dy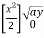
= dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2dy
dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2dy
= (4a2 y – 4ay2 + y3) dy + y2dy
=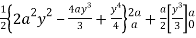
= +
+ 
= a4
Question-6: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
Sol. Let,
y² = 4ax ………………..(1)
And
x² = 4ay…………………..(2)
Then if we solve these equations , we get the values of points where these two curves intersect

x varies from y²/4a to  and y varies from o to 4a,
and y varies from o to 4a,
Now using the conceot of double integral,
Area = 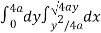
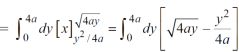

Question-7: Calculate the volume generated by the revolution of a cardioid,
r = a ( 1 – cosθ) about its axis
Sol. Here,
r = a ( 1 – cosθ)
Volume = 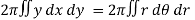
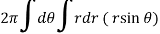
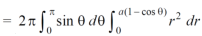
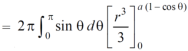
=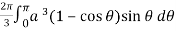
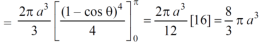
Which is the volume of generated by cardioid.
Question-8: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
Sol. We know that,
Volume = 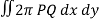
Here , PQ = 3 – x,
= 
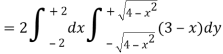
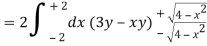
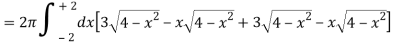
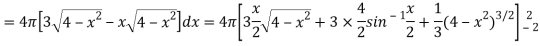
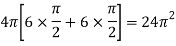
The volume is 24π².
Question-9: Find the mass of a plate formed by the coordinate planes and the plane-
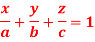
The variable density 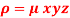
Sol.
Here we the mass will be-
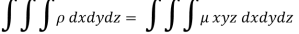
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.
Therefore the required mass will be-
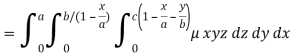


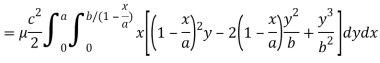
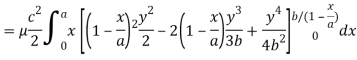
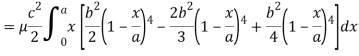
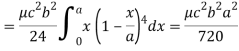
Which is the required answer.
Question-10: Determine the coordinates of the centroid of the area lying between the curve y = 5x - x² and the x-axis.
Sol.
Here y = 5x - x²when y = 0, x = 0 or x = 5
Therefore the curve cuts the x-axis at 0 and 5 as in the figure-
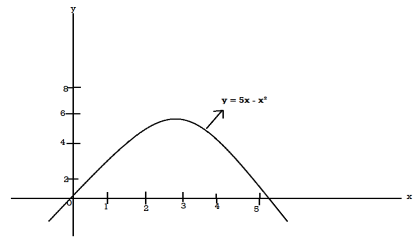

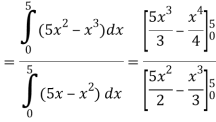

Now
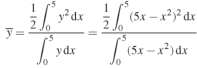
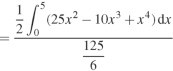
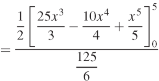
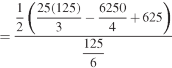
= 2.5
Therefore the centroid of the area lies at (2.5, 2.5)
Question-11: Evaluate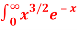 dx
dx
Solution dx =
dx =  dx
dx
= γ(5/2)
= γ(3/2+ 1)
= 3/2 γ(3/2 )
= 3/2. ½ γ(½ )
= 3/2. ½ π
= ¾ π
Question-12: Evaluate  dx.
dx.
Solution: Let 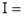
 dx.
dx.
x | 0 |  |
t | 0 |  |
Put  or
or  ; 4x dx = dt
; 4x dx = dt
 dx
dx

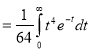
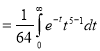
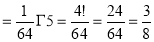
Question-13: Evaluate
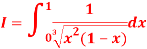
Solution:
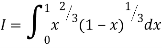
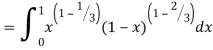


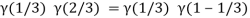
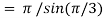
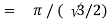
= 2 π/3
Question-14: Evaluate
Solution :Let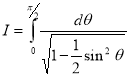
Put 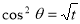 or
or  ,
,
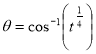 ,
,
When ,
, ;
;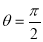 ,
,
Also
 | o | 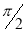 |
 | 1 | 0 |


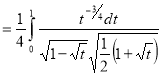
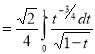
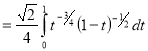
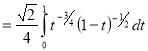


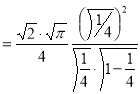
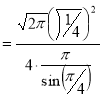
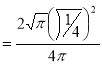

Question-15: Prove that-

Where a>0.
Sol.
We know that-

Put m – 1 = 1 or m = 2
We get-
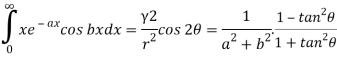
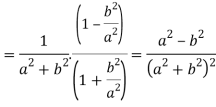
Hence proved