Unit - 1
Vector spaces
Q1) Define vector space.
A1)
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 
(b) 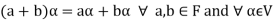
(c) 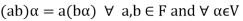
(d) If 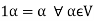 then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Q2) Suppose V(F) is a vector space and 0 be the zero vector of V. Then prove that 
A2)
We have
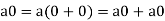
We can write 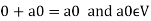
So that,
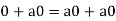
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
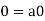
Q3) What are the necessary and sufficient conditions for subspace?
A3)
The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 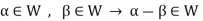
2. 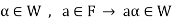
Proof:
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
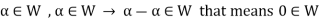
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 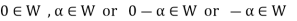
So that the additive inverse of each element of W is also in W.
So that-

Thus W is closed with respect to vector addition.
Q4) The intersection of any two subspaces  and
and  of a vector space V(F) is also a subspace of V(F).
of a vector space V(F) is also a subspace of V(F).
A4)
As we know that 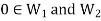 therefore
therefore 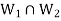 is not empty.
is not empty.
Suppose  and
and 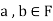
Now, 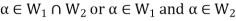
And 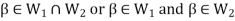
Since 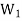 is a subspace, therefore-
is a subspace, therefore-
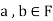 and
and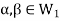 then
then 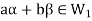
Similarly, 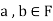
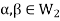 then
then
Now 
Thus,
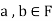 And
And 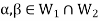
Then 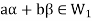
So that 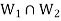 is a subspace of V(F).
is a subspace of V(F).
Q5) Define a subspace.
A5)
A subset W of a vector space V over a field F is called a subspace of V if W is a vector space over F with the operations of addition and scalar multiplication defined on V.
In any vector space V, note that V and {0 } are subspaces. The latter is called the zero subspace of V.
Q6) What are symmetric and skew symmetric matrices?
A6)
The transpose 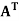 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,

Then
Transpose of this matrix,
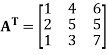
A symmetric matrix is a matrix A such that 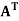 = A.
= A.
A skew- symmetric matrix is a matrix A such that 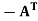 = A.
= A.
Q7) Define sum and direct sum.
A7)
Sum- If S1 and S2 are nonempty subsets of a vector space V, then the sum of S1 and S2, denoted S1+S2, is the set {x + y : x ∈ S1 and y ∈ S2}.
Direct sum- A vector space V is called the direct sum of W1 and W2 if W1 and W2 are subspaces of V such that W1 ∩W2 = {0} and W1 +W2 = V. We denote that V is the direct sum of W1 and W2 by writing V = W1 ⊕ W2.
Q8) What do you understand by linear combinations of vectors?
A8)
Suppose V(F) be a vector space. If 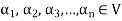 , then any vector-
, then any vector-
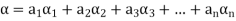
Where 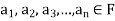
Is called a linear combination of the vectors 
Q9) The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S.
A9)
Suppose  be any two elements of L(S).
be any two elements of L(S).
Then
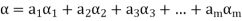
And 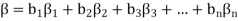
Where a and b are the elements of F and  are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
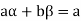 (
(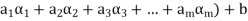 (
(
 (
( (
(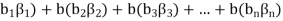
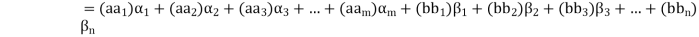
Thus 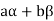 has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set 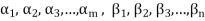 of the elements of S.
of the elements of S.
Consequently 
Thus, 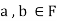 and
and  so that
so that 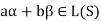
Hence L(S) is a subspace of V(F).
Q10) What is linear dependence and linear independence?
A10)
Linear dependence-
Let V(F) be a vector space.
A finite set 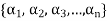 of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars 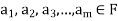 (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-
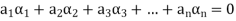
Linear independence-
Let V(F) be a vector space.
A finite set 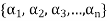 of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
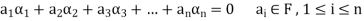
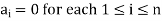
Q11) The set of non-zero vectors 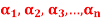 of V(F) is linearly dependent if some
of V(F) is linearly dependent if some 
Is a linear combination of the preceding ones.
A11)
If some 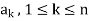
Is a linear combination of the preceding ones, 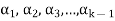 then ∃ scalars
then ∃ scalars 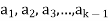 such that-
such that-
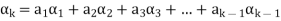 …… (1)
…… (1)
The set {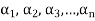 } is linearly dependent because the linear combination (1) the scalar coefficient
} is linearly dependent because the linear combination (1) the scalar coefficient 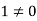
Hence the set {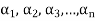 } of which {
} of which {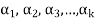 } is a subset must be linearly dependent.
} is a subset must be linearly dependent.
Q12) Show that S = {(1, 2, 4) , (1, 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space  . Where R is the field of real numbers.
. Where R is the field of real numbers.
A12)
Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Q13) If 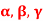 are linearly independent vectors of V(F) where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F) where F is the field of complex numbers, then so also are  .
.
A13)
Suppose a, b, c are scalars such that-

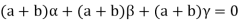 …………….. (1)
…………….. (1)
But 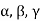 are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-

The coefficient matrix A of these equations will be-
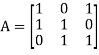
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that 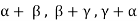 are also linearly independent.
are also linearly independent.
Q14) State and prove dimension theorem for vector spaces.
A14)
Statement- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
Proof: Let V(F) is a finite dimensional vector space. Then V possesses a basis.
Let  and
and  be two bases of V.
be two bases of V.
We shall prove that m = n
Since V = L(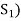 and
and 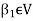 therefore
therefore 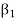 can be expressed as a linear combination of
can be expressed as a linear combination of 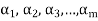
Consequently, the set 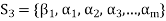 which also generates V(F) is linearly dependent. So that there exists a member
which also generates V(F) is linearly dependent. So that there exists a member 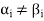 of this set. Such that
of this set. Such that 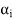 is the linear combination of the preceding vectors
is the linear combination of the preceding vectors 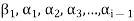
If we omit the vector 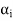 from
from  then V is also generated by the remaining set.
then V is also generated by the remaining set.
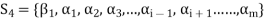
Since V = L(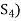 and
and 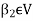 therefore
therefore 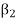 can be expressed as a linear combination of the vectors belonging to
can be expressed as a linear combination of the vectors belonging to 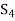
Consequently the set-
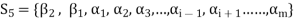
Is linearly dependent.
Therefore there exists a member 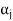 of this set such that
of this set such that 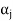 is a linear combination of the preceding vectors. Obviously
is a linear combination of the preceding vectors. Obviously  will be different from
will be different from 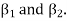
Since {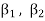 } is a linearly independent set
} is a linearly independent set
If we exclude the vector  from
from 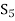 then the remaining set will generate V(F).
then the remaining set will generate V(F).
We may continue to proceed in this manner. Here each step consists in the exclusion of an 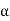 and the inclusion of
and the inclusion of 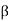 in the set
in the set 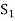
Obviously the set 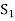 of all
of all 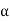 can not be exhausted before the set
can not be exhausted before the set 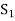 and
and 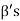
Otherwise V(F) will be a linear span of a proper subset of 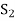 thus
thus 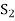 become linearly dependent. Therefore we must have-
become linearly dependent. Therefore we must have-
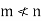
Now interchanging the roles of 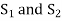 we shall get that
we shall get that 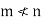
Hence,
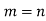
Q15) State and prove extension theorem.
A15)
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose 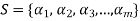 be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 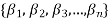
Let us consider a set-
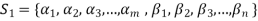 …………. (1)
…………. (1)
Obviously L(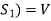 , since there
, since there  can be expressed as linear combination of
can be expressed as linear combination of 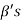 therefore the set
therefore the set 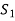 is linearly dependent.
is linearly dependent.
So that there is some vector of 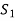 which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 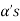 since the
since the 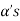 are linearly independent.
are linearly independent.
Therefore this vector must be some 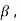 say
say 
Now omit the vector 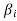 from (1) and consider the set-
from (1) and consider the set-
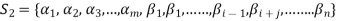
Obviously L( . If
. If 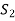 is linearly independent, then
is linearly independent, then  will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If 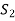 is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing 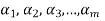 and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of 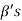 will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Q16) What is null space?
A16)
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-
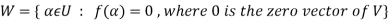
The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Q17) The mapping 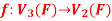 defined by-
defined by-
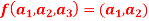
Is a linear transformation  .
.
What is the kernel of this linear transformation.
A17)
Let 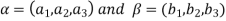 be any two elements of
be any two elements of 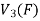
Let a, b be any two elements of F.
We have
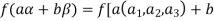 (
(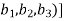
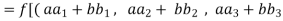
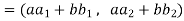
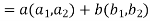 =
= 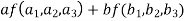
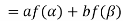
So that f is a linear transformation.
To show that f is onto 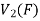 . Let
. Let 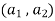 be any elements
be any elements 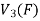 .
.
Then 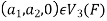 and we have
and we have 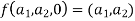
So that f is onto 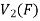
Therefore f is homomorphism of  onto
onto 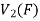 .
.
If W is the kernel of this homomorphism then 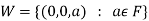
We have
∀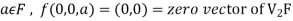
Also if  then
then 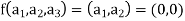
Implies 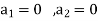
Therefore 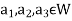
Hence W is the kernel of f.
Q18) What is rank nullity theorem?
A18)
Statement:
Let A is a matrix of order m by n, then-
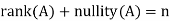
Proof:
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let  represent these free variables and let
represent these free variables and let 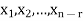 denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 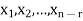
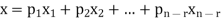
Which shows that 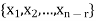 spans null-space (A).
spans null-space (A).
Thus 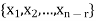 is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Q19) Let V and W be vector spaces, and let T: V → W be linear. Then T is one-to-one if and only if N(T) = {0}.
A19)
Suppose that T is one-to-one and x ∈ N(T). Then T(x) = 0 = T(0 ). Since T is one-to-one, we have x = 0 . Hence N(T) = {0 }.
Now assume that N(T) = {0 }, and suppose that T(x) = T(y). Then 0 = T(x) − T(y) = T(x − y).
Therefore x − y ∈ N(T) = {0 }. So x − y = 0, or x = y. This means that T is one-to-one.