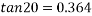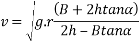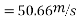Unit-05
Kinetics of circular motion
Q1)1 Define
- Angular velocity
- Angular acceleration
- Centripetal force
- Centrifugal force
Ans. Angular velocity
It is defined as rate of change of angular displacement of body. It is denoted by 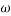 .
.
Angular displacement is always measured in terms of angle covered by body from initial position.
Consider a body moving along a circular path as shown in figure 1
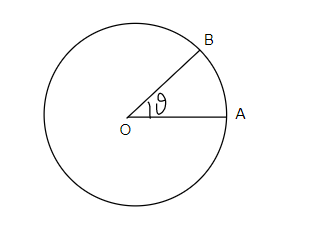
Consider a body initially at position A and after time t body moves to position B.
Let
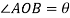
Angular displacement=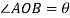
Time taken=t
Angular velocity=

Mathematically
Angular velocity=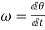
Angular velocity is expressed in terms of revolutions describe in one minutes.
Angular acceleration:-
It is defined as the rate of change of angular velocity. It is measured as radians per second hand written as 
It is denoted as 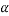
Mathematically,
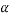 =Rate of change of angular velocity
=Rate of change of angular velocity
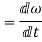
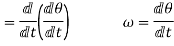

Also,
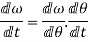
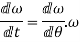
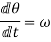
 angular acceleration
angular acceleration
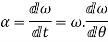
Centripetal force:-
A body moving in circle or along a circular path with constant velocity suffers a continuous change in its direction at every point of its motion but magnitude of its speed remains constant since velocity is vector quantity i.e. magnitude and direction both are considered and velocity of body is continuously changing due to change in direction; therefore according to Newton’s first law of motion an external force must act continuously upon body to produce a change in direction of moving body.
Due to inertia body tends to move along the tangent at every point of its motion with constant velocity. Therefore some force must act at right angles to direction of motion at every point, which should be change the direction of motion of body leaving speed uniform.
Thus the force which act along radius of circle at every point and is always directed towards centre of circle along which body moves is known as centripetal force.
Centrifugal force:-
According to Newton’s third law of motion, the force which acts opposite to centripetal force is known as centrifugal force.
Centrifugal force always acts away from centre of path i.e. centrifugal force always tends to throw the body away from centre of circular path.
Q2)2 Derive maximum velocity to avoid overturning of vehicle
Ans. Maximum velocity to avoid over it earning of vehicle moving along a level circular path
Consider a vehicle moving on a level circular path with O as a centre as shown in figure 4
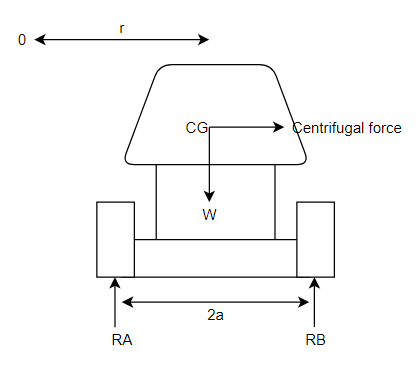
Let
m=mass of vehicle
v=velocity of vehicle
r=radius of circular path in m.
h=height of C.G. Of vehicle from ground level in m.
2a=distance between reactions A and B
 reaction at A
reaction at A
 =reaction at B
=reaction at B
We know that centrifugal force acting through C.G. Of vehicle

Also
Weight of vehicle=mg acting downward through its centre of gravity will exert reaction equal to 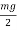 on A and B (because of symmetry) taking moment about A and equating the same
on A and B (because of symmetry) taking moment about A and equating the same
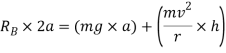
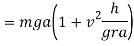
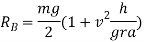
Similarly by taking moment about B and equating the same we get
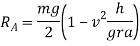
Little consideration will show that reaction at B. I.e.  can never be negative. But reaction at A i.e.
can never be negative. But reaction at A i.e. 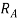 can be negative if value of
can be negative if value of 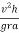 becomes more than unity if we observe
becomes more than unity if we observe 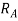 we can say that
we can say that 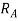 can be negative if value of v is increase, all other things are constant.
can be negative if value of v is increase, all other things are constant.
When this condition reaches, the vehicle will overturn at wheel B. Therefore in order to avoid overturning

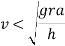
In order to avoid overturning velocity of vehicle is less than that obtained from above equation the vehicle will not overturn if velocity is more vehicle is bound to overturn.
Therefore to avoid overturn maximum velocity is given
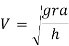
Q3)3 Derive max velocity to avoid skilling away of vehicle moving along a level of circular path
Ans. Maximum velocity to avoid skidding away of vehicle moving along a level of circular path
Consider a vehicle moving on a level circular path with O as shown in figure 4
Let
m=mass of vehicle
v=velocity of vehicle
r=radius of circular path in in m.
 =Coefficient of friction between the wheels of vehicle and ground
=Coefficient of friction between the wheels of vehicle and ground
We know that,
Centrifugal force which tends to skid away the vehicle
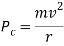
And friction force between the wheels of vehicle and ground
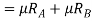
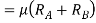
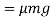
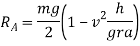
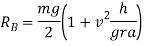
The skidding away can only be avoiding if frictional force is more than centrifugal force. Therefore in order to avoid skidding away.


It is thus obvious that if velocity is less than that obtained from above equation, the vehicle will not skid away. But velocity is more than that of obtain from above equation, vehicle will skid away.
Therefore, in order to avoid skidding maximum velocity

Q4)4 A car weighing 15 KN goes around a flat curve of 50m radius. The distance between inner and outer wheel is I.S and C.G IS 0.75m above road level. What is limiting speed of car on this curve? Determine normal reactions developed at inner and outer wheels if car negotiates the curve with speed of 40km/h.
Take u=0.4
Ans. Consider dynamic equilibrium of car forces acting on which are shown before
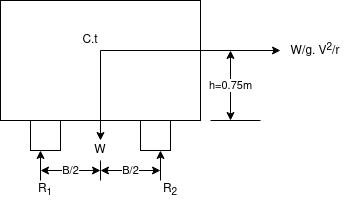
Limiting speed v from consideration of avoiding is given by
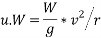
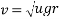
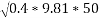
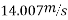
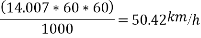
Limiting speed from consideration of avoiding overturning
Taking moment about point of contact of outer wheel with road and voting that  when vehicle is about to overturn
when vehicle is about to overturn
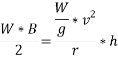
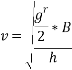
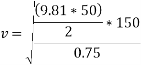

Speed limit should be 50.42 km/h
If vehicle moves with velocity of 40km/h
V=40km/h
11.11m/s
Taking moment about outer wheel
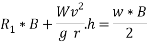
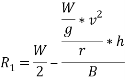
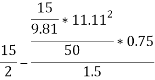
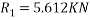
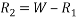
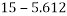

Q5)5 a riding at 5m/s has turn a corner. What is least radius of curve he has to describe if coefficient of friction between tyres and road be 0.25
Ans. velocity of cyclist (v) =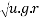
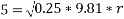
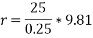
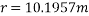
Q6)6 Find at what speed a vehicle can move round a curve of 40m . Radius without side ship
- On level road
- On a road banked to an inclination of lin 10
Ans. given r=40m
U=0.4
- On level road limiting speed from consideration of avoiding skidding is given by
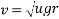
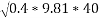
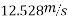
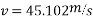
2. On banked road to inclination of lin 10 tan x=1/10 =0.1
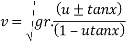
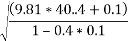
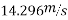

Q7)7 A vehicle weighing 10 KN is to turn circular corner of radius 100m on a level ground with speed of 10m/s. The height of C.G above road is 1m and distance between wheel is 1.5 m at what max speed it can travel corner without fear of overturning also find reactions at wheel.
Ans. limiting speed from consideration of avoiding overturning
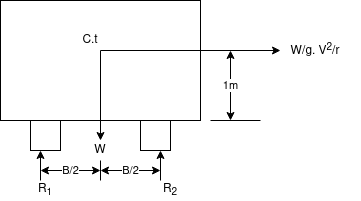
Taking moment about point of contact of outer wheel with road and voting that 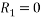
When vehicle is about to overturn
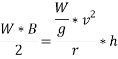
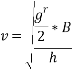
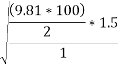
=27.12 m/s
Taking moment about outer wheel
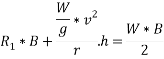

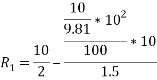
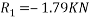
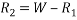
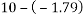
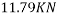
Q8)8 Find the limiting speed of vehicle on a curve of 100m radius from the consider ration of overturning on
- Level road
- If 20 degree bank is provided
Take weight of vehicle =15KN distance between center of inner and outer of wheel =1.5m height of C.G above road surface =0.65m and u=0.5
Ans. –
- On level road
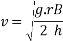
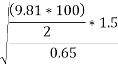
Ii.  banking is provide
banking is provide