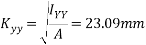Unit 03

Centroid and moment of inertia

Que-1 Fig. Shown an area ABCDEF

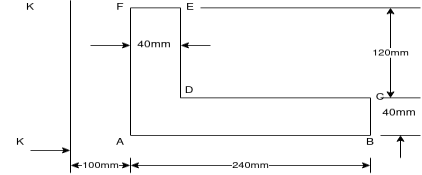
Compute the moment of inertia of above area about axis K-K

Ans- as M.I is required to find about axis K-K there is no need to find C.K of area.

Consider above fig. As 2 rectangles as shown below

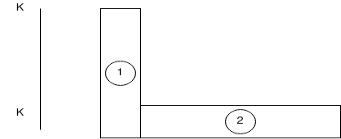
We know that M.I of section 1 about its C.G and parallel to axis K-K

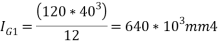
Distance between CG of section 1 and axis k-k

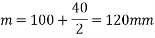
M.I of section 1 about axis K-K

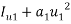
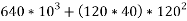
Similarly

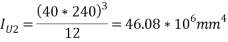
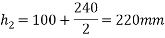
M.I of section 2 about axis K-K

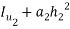
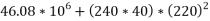
M.I of whole area about axis K-K

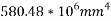
Ques 2- Determine the moment of inertia of symmetric I-section about its centroid axis x-x and y-y

Ans- the section is divided into three rectangles

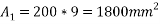
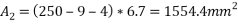
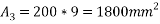
Total area =A=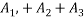

=5154.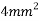

As section is symmetrical about x-x axis and y-y axis

Centroid will coincide with centroid of rectangle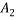

w.r.t centroids axis x-x and y-y the centroid of rectangle and that of for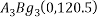

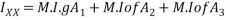about x-x axis

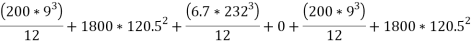
59269202 mm

Similarly

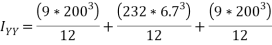
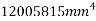
Que-3 Determine moment of inertia of built up section shown in fig. About its centroidal axis x-x and y-y.

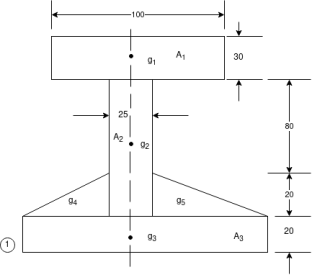
Ans- divide given section into rectangle3s and triangles due to symmetrical centroid on axis y-y . a reference axis 1-1is choose as shown on fig

The distance of centroidal axis from 1 – 1

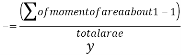
=59.26mm

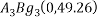With reference to centroidal axis x-x and y-y the centroidal of rectangle that of from from 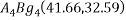and that of 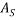is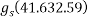

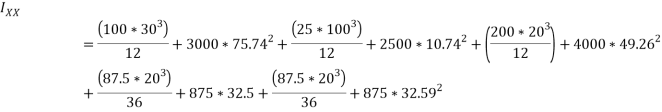
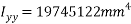
Que-4 Find second moment of  shaded portion shown in fig. About its centroidal axis.

Ans – the section B divided into rectangles and triangle and semi- circle

Total area =area of triangle ABC + area of rectangle ACDE – area of semicircle

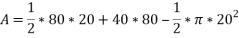
=3371.68 mm

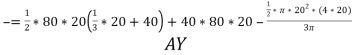
=95991.77

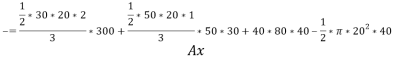
=132203.6

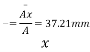
M.I about centroidal x-x axis= M.I of triangle ABC + M.I of rectangle-M.I of semicircle

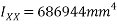
Similarly

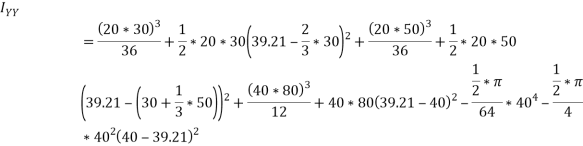
=1868392

Que-5 Determine moment of inertia of section shown below about axis possible through centroid and parallel to top most fibre of section also determine moment  of inertia about axis of symmetry . Hence find radii of gyration

Ans- give composite section can be divided into two rectangles

Area

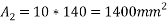
Total area =A=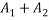

2900

Due to symmetry centroid lies on symmetric axis y-y

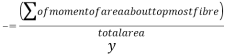
=41.21 mm

The centroid of 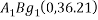and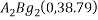

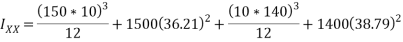
6372442.5

Similarly

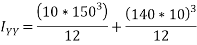
=2824166.7 mm

Hence, M.I of section about an axis passing through centroid and parallel to top most fibre B 

Radius of gyoation (k)=

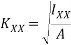
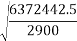
=46.88mm

Similarly

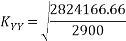
=31.21mm

Que-6 Determine polar moment of inertia about centroidal axis of I section . Also determine radii of gyration with respect to x-x axis and y-y axis

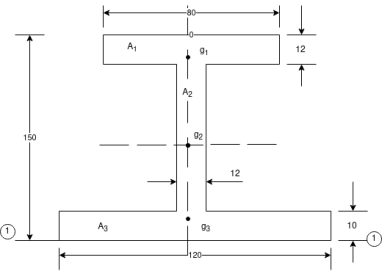
Ans – the section B divided into three parts (rectangles)

Area

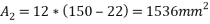
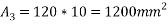
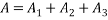
=3696 due to symmetric centroid lies on axis y-y the bottom fibre 1-1 is choose as reference axis to locate centroid

The distance of centroid from 1-1

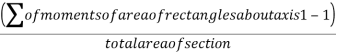
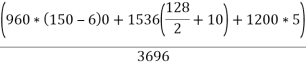
69.78 mm

With reference with centroidle axis x-x and y-y the centroidal of reactangle   , and

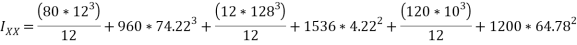
=12470028mm

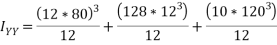
1970432mm

Polar moment of inertia =

14440454 mm