undefined | unit 3 finite element analysis

CAD

Unit 3

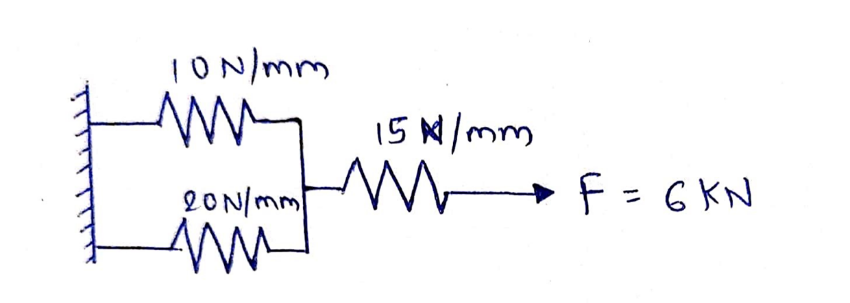
Q.1 Fig shows a cluster of 3 springs. Using finite element method, determine: 1) the deflection of each spring and 2) the reaction force at support.

Solution:

Given: k1 = 10 N/mm

k2 = 20 N/mm

k3 = 15 N/mm

U1 = 0

P3 = 6000 N

Discretization

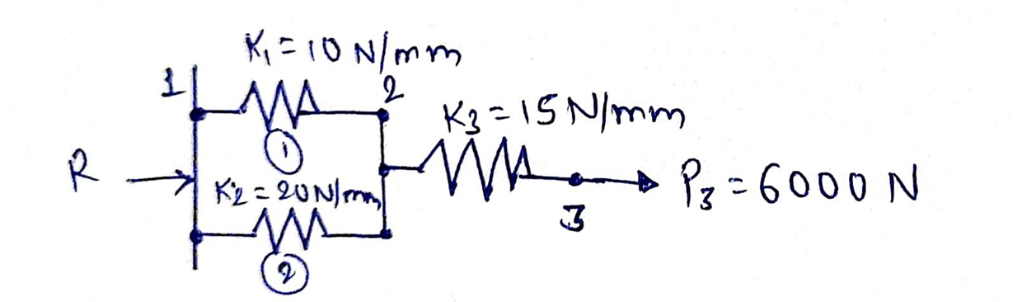
Three springs can be treated as three 1D spar element

Element Number	Global Node number ‘n’ of
Element Number	Local Node 1	Local Node 2
1	1	2
2	1	2
3	2	3

2. Element stiffness matrix

For Element 1,

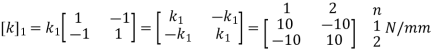
For Element 2,

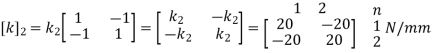
For Element 3,

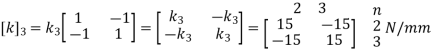
3. Global stiffness matrix

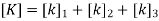
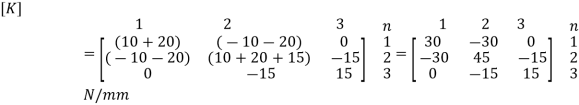
4. Global load vector

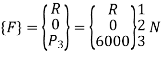
5. Global nodal displacement vector

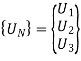
6. Global stiffness-nodal displacement relationship

Hence after the assembly, the equilibrium equation is,

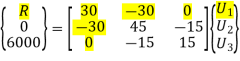
At node 1, U1 = 0, there is rigid support.

Using elimination approach, first rows and columns are eliminated.

7. Nodal Displacements

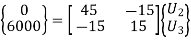
Solving two equations for two unknowns, we get,

U2 = 200 mm and U3 = 600 mm

Deflection of Spring 1 = U2 – U1 = 200 – 0 = 200 mm

Deflection of Spring 2 = U2 – U1 = 200 – 0 = 200 mm

Deflection of Spring 3 = U3 – U2 = 600 – 200 = 400 mm

8. Reaction force at support

We have,

30U1 – 30U2 = R

30 x 0 – 30 x 200 = R

R = -6000 N

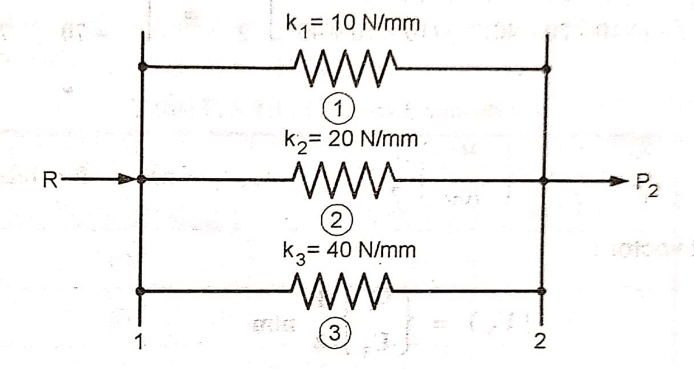
Q.2 Fig shows a cluster of 3 springs having stiffness 10, 20 and 40 N/mm, all connected in parallel. One end of assembly is fixed and force of 700 N is applied at other end. Using finite element method, determine the deflection of each spring.

Solution:

Given: k1 = 10 N/mm

k2 = 20 N/mm

k3 = 40 N/mm

U1 = 0

P2 = 700 N

Discretization

Three springs can be treated as three 1D spar element

Element Number	Global Node number ‘n’ of
Element Number	Local Node 1	Local Node 2
1	1	2
2	1	2
3	1	2

2. Element stiffness matrix

For Element 1,

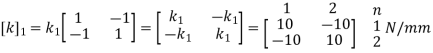
For Element 2,

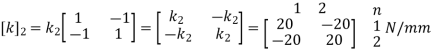
For Element 3,

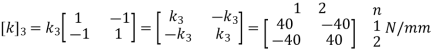
3. Global stiffness matrix

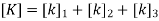
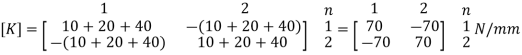
4. Global load vector

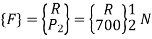
5. Global nodal displacement vector

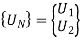
6. Global stiffness-nodal displacement relationship

Hence after the assembly, the equilibrium equation is,

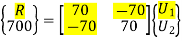
At node 1, U1 = 0, there is rigid support.

Using elimination approach, first rows and columns are eliminated.

7. Nodal Displacements

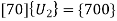
Solving the equation, we get,

U2 = 10 mm

Deflection of all Springs = U2 – U1 = 10 – 0 = 10 mm

Q.3 Fig shows a cluster of three springs. Using the finite element method, determine:

1) The deflection of each spring

2) The reaction force at support

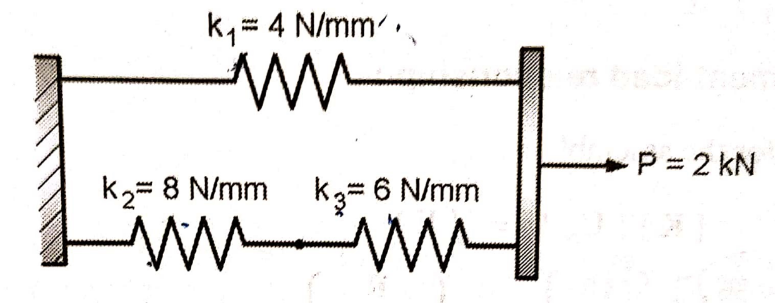
Solution:

Given: k1 = 4N/mm

k2 = 8N/mm

k3 = 6N/mm

U1 = 0

P3 = 2000 N

Discretization

Three springs can be treated as three 1D spar element

Element Number	Global Node number ‘n’ of
Element Number	Local Node 1	Local Node 2
1	1	3
2	1	2
3	2	3

2. Element stiffness matrix

For Element 1,

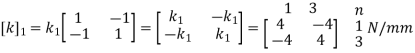
For Element 2,

For Element 3,

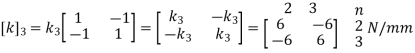
3. Global stiffness matrix

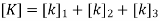
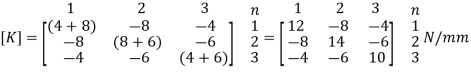
4. Global load vector

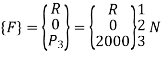
5. Global nodal displacement vector

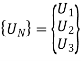
6. Global stiffness-nodal displacement relationship

Hence after the assembly, the equilibrium equation is,

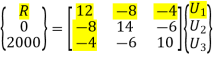
At node 1, U1 = 0, there is rigid support.

Using elimination approach, first rows and columns are eliminated.

7. Nodal Displacements

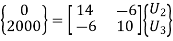
Solving two equations for two unknowns, we get,

U2 = 115.38 mm and U3 = 269.23 mm

Deflection of Spring 1 = U3 – U1 = 269.23 – 0 = 269.23 mm

Deflection of Spring 2 = U2 – U1 = 115.38 – 0 = 115.38 mm

Deflection of Spring 3 = U3 – U2 = 269.23 – 115.38 = 153.84 mm

8. Reaction force at support

We have,

12U1 – 8U2 – 4U3 = R

12 x 0 – 8 x 115.38 – 4 x 269.23 = R

R = -2000 N

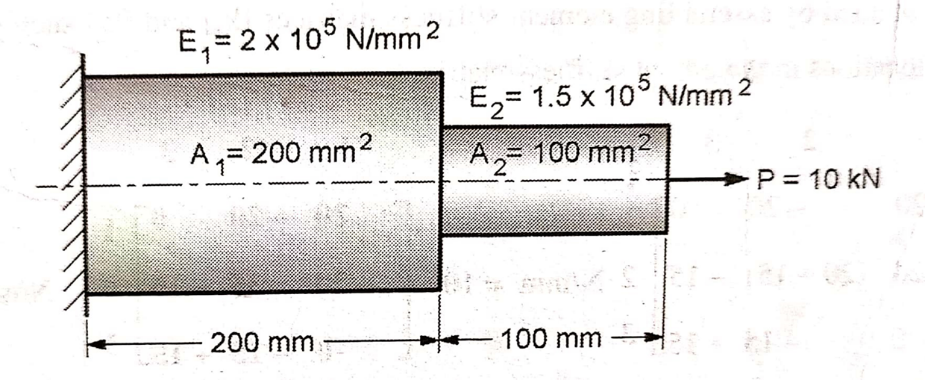
Q.4 An axial step bar is shown in figure. Determine the deflection, stresses in element and reaction force.

Solution:

Given: l1 = 200 mm

l2 = 100 mm

A1 = 200 mm2

A2 = 100 mm2

E1 = 2 x 105 N/ mm2

E2 = 1.5 x 105 N/ mm2

P = 10000 N

Discretization

Fig shows an assemblage of two 1D spar element. Its elemental connectivity is given below

Element Number	Global Node number ‘n’ of
Element Number	Local Node 1	Local Node 2
1	1	2
2	2	3

2. Element stiffness matrix

For Element 1,

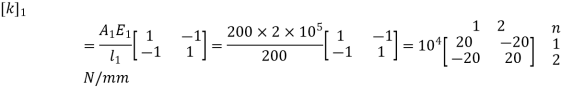
For Element 2,

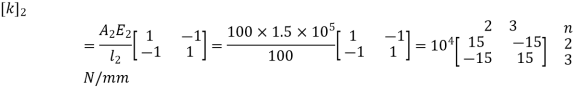
3. Global stiffness matrix

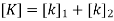
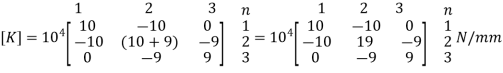
4. Global load vector

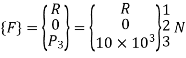
5. Global nodal displacement vector

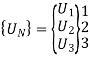
6. Global stiffness-nodal displacement relationship

Hence after the assembly, the equilibrium equation is,

At node 1, U1 = 0, there is rigid support.

Using elimination approach, first rows and columns are eliminated.

7. Nodal Displacements

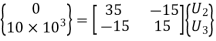
Solving two equations for two unknowns, we get,

U2 = 0.05 mm and U3 = 0.117 mm

8. Stresses in elements:

Stresses are given by,

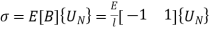
In element 1,

In element 2,

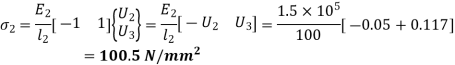
9. Reaction force at support

We have,

104 (20U1 – 20U2 ) = R

104 (20 x 0 – 20 x 0.05) = R

R = -10 x 103 kN

Q.5 A stepped bimetallic bar with circular cross-section is shown in fig, is subjected to an axial pull of 10 kN. Determine:

1) the nodal displacement 2) elements stress and

3) the support reaction

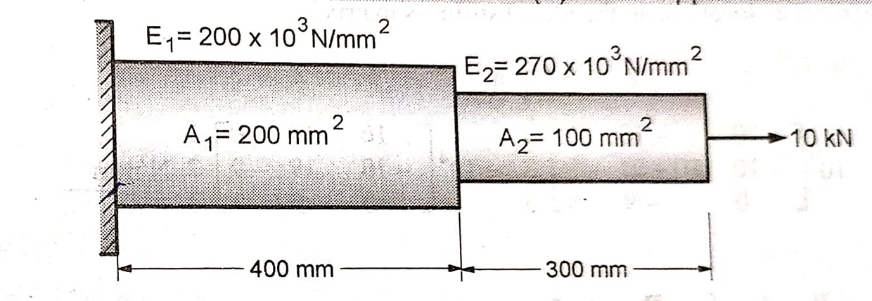
Solution:

Given: l1 = 400 mm

l2 = 300 mm

A1 = 200 mm2

A2 = 100 mm2

E1 = 200 x 103 N/ mm2

E2 = 270 x 103 N/ mm2

P = 10000 N

Discretization

Fig shows an assemblage of two 1D spar element. Its elemental connectivity is given below

Element Number	Global Node number ‘n’ of
Element Number	Local Node 1	Local Node 2
1	1	2
2	2	3

2. Element stiffness matrix

For Element 1,

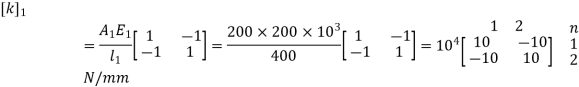
For Element 2,

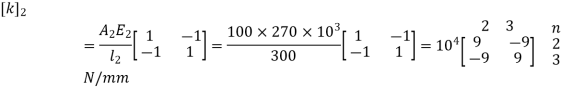
3. Global stiffness matrix

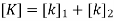
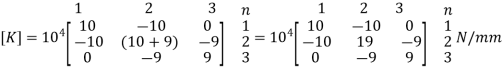
4. Global load vector

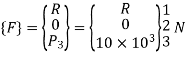
5. Global nodal displacement vector

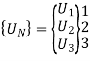
6. Global stiffness-nodal displacement relationship

Hence after the assembly, the equilibrium equation is,

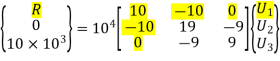
At node 1, U1 = 0, there is rigid support.

Using elimination approach, first rows and columns are eliminated.

7. Nodal Displacements

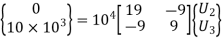
Solving two equations for two unknowns, we get,

U2 = 0.1 mm and U3 = 0.211 mm

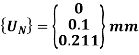
8. Stresses in elements:

Stresses are given by,

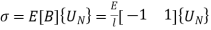
In element 1,

In element 2,

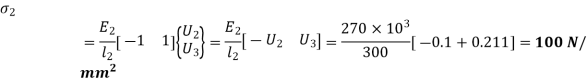
9. Reaction force at support

We have,

104 (10U1 – 10U2 ) = R

104 (10 x 0 – 10 x 0.1) = R

R = -10 x 103 kN

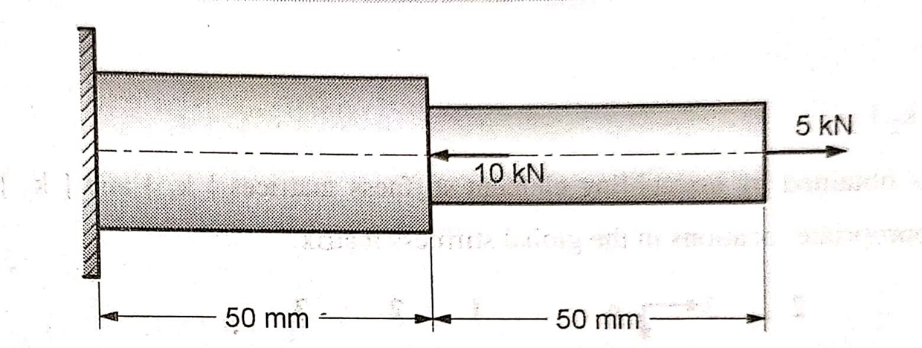
Q.6 Find the stresses in a stepped bimetallic bar, shown in figure, due to forces 10kN and 5kN. Use following data:

l1 = 50 mm A1 = 150 mm2 E1 = 200 x 103 N/ mm2

l2 = 50 mm A2 = 100 mm2 E2 = 70 x 103 N/ mm2

Solution:

Given:

l1 = 50 mm A1 = 150 mm2 E1 = 200 x 103 N/ mm2

l2 = 50 mm A2 = 100 mm2 E2 = 70 x 103 N/ mm2

Discretization

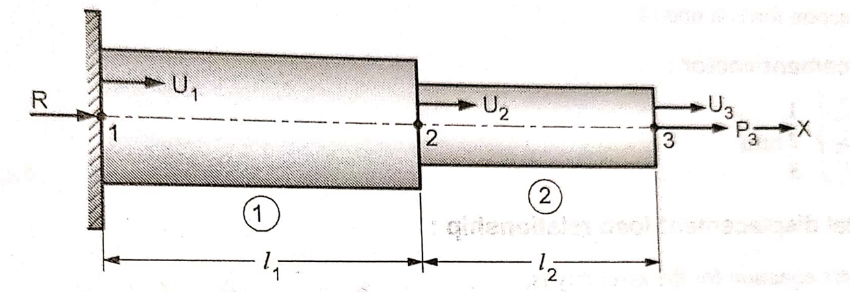
Fig shows an assemblage of two 1D spar element. Its elemental connectivity is given below

Element Number	Global Node number ‘n’ of
Element Number	Local Node 1	Local Node 2
1	1	2
2	2	3

2. Element stiffness matrix

For Element 1,

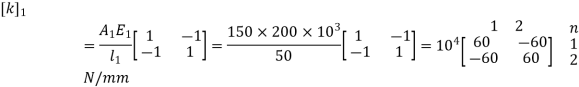
For Element 2,

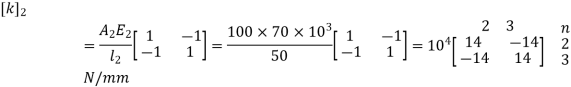
3. Global stiffness matrix

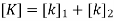
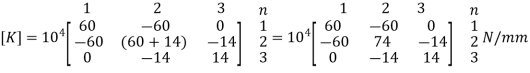
4. Global load vector

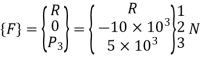
5. Global nodal displacement vector

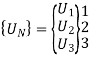
6. Global stiffness-nodal displacement relationship

Hence after the assembly, the equilibrium equation is,

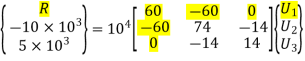
At node 1, U1 = 0, there is rigid support.

Using elimination approach, first rows and columns are eliminated.

7. Nodal Displacements

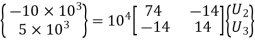
Solving two equations for two unknowns, we get,

U2 = -8.33 x 10-3 mm and U3 = 27.4 x 10-3 mm

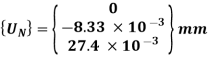
8. Stresses in elements:

Stresses are given by,

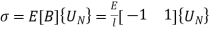
In element 1,

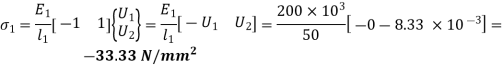
In element 2,

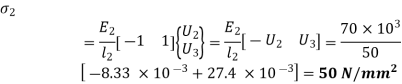
9. Reaction force at support

We have,

104 (60U1 – 60U2 ) = R

104 (60 x 0 – 60 x (-8.33 x 10-3)) = R

R = -5 x 103 kN

Q.7 What is shape Function?

Solution: The values of the field variable computed at the nodes are used to approximate the values at non-nodal points (that is, in the element interior) by interpolation of the nodal values. For the three-node triangle example, the field variable is described by the approximate relation

φ(x, y) = N1(x, y) φ1+ N2(x, y) φ2+ N3(x, y) φ3

where φ1, φ2, andφ3are the values of the field variable at the nodes, and N1, N2, and N3are the interpolation functions, also known as shape functions or blending functions.

In the finite element approach, the nodal values of the field variable are treated as unknown constants that are to be determined. The interpolation functions are most often polynomial forms of the independent variables, derived to satisfy certain required conditions at the nodes.

The interpolation functions are predetermined, known functions of the independent variables; and these functions describe the variation of the field variable within the finite element.

Let 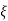be the natural coordinate of 1D element, then the shape functions are given by

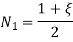
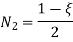
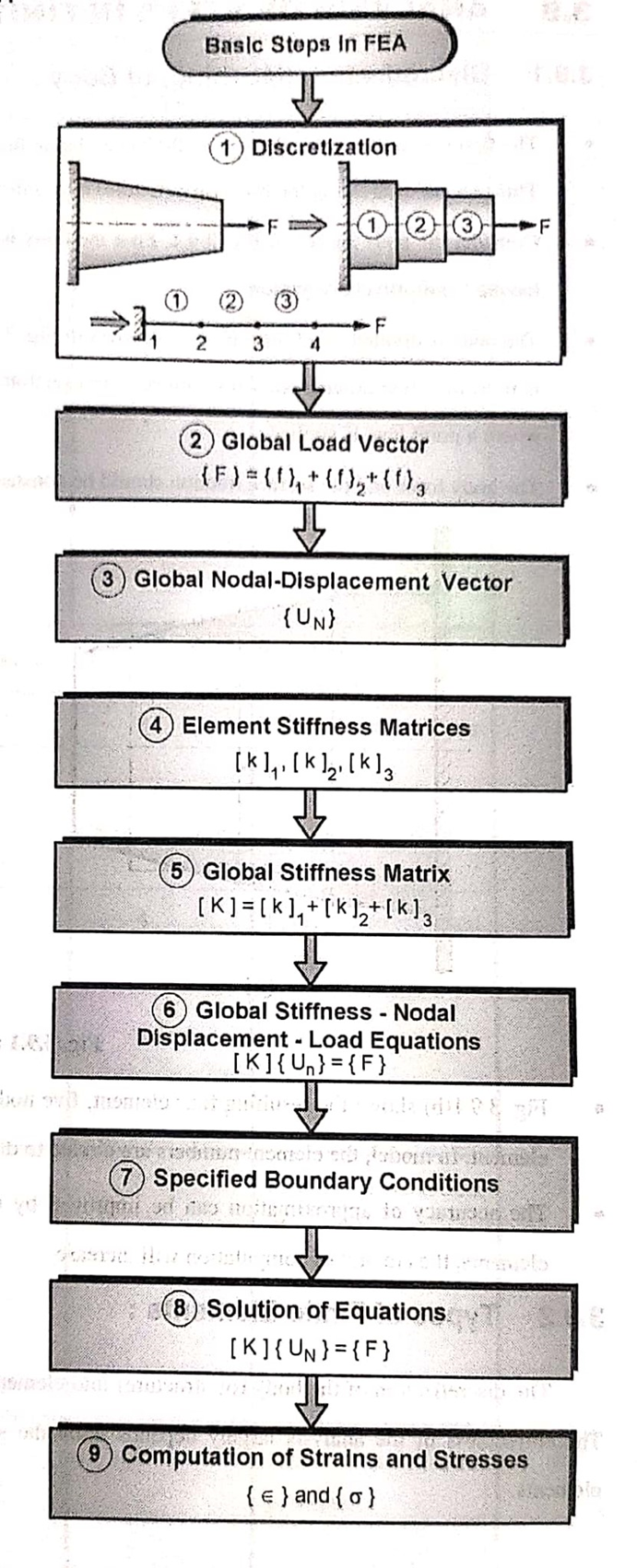
Q. 8 Discuss the general procedure of FEM.

Solution: To summarize in general terms how the finite element method works we list main steps of the finite element solution procedure below.

Discretize the continuum: The first step is to divide a solution region into finite elements. The finite element mesh is typically generated by a preprocessor program. The description of mesh consists of several arrays main of which are nodal coordinates and element connectivities.

Select interpolation functions: Interpolation functions are used to interpolate the field variables over the element. Often, polynomials are selected as interpolation functions. The degree of the polynomial depends on the number of nodes assigned to the element.

Find the element properties: The matrix equation for the finite element should be established which relates the nodal values of the unknown function to other parameters. For this task different approaches can be used; the most convenient are: the variational approach and the Galerkin method.

Assemble the element equations: To find the global equation system for the whole solution region we must assemble all the element equations. In other words we must combine local element equations for all elements used for discretization. Element connectivities are used for the assembly process. Before solution, boundary conditions (which are not accounted in element equations) should be imposed.

Solve the global equation system: The finite element global equation system is typically sparse, symmetric and positive definite. Direct and iterative methods can be used for solution. The nodal values of the sought function are produced as a result of the solution.

Compute additional results: In many cases we need to calculate additional parameters. For example, in mechanical problems strains and stresses are of interest in addition to displacements, which are obtained after solution of the global equation system.

Q.9 Explain discretization technique.

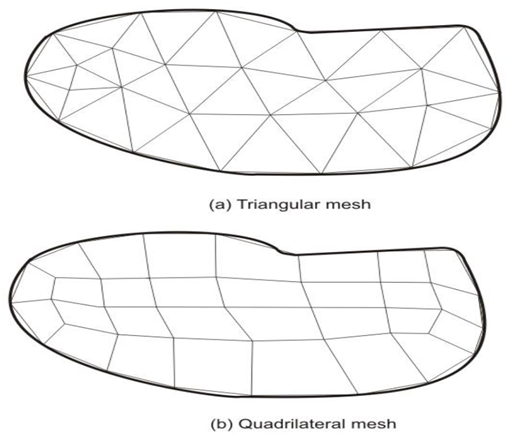
Solution: The need of finite element analysis arises when the structural system in terms of its either geometry, material properties, boundary conditions or loadings is complex in nature. For such case, the whole structure needs to be subdivided into smaller elements. The whole structure is then analyzed by the assemblage of all elements representing the complete structure including its all properties. The subdivision process is an important task in finite element analysis and requires some skill and knowledge. In this procedure, first, the number, shape, size and configuration of elements have to be decided in such a manner that the real structure is simulated as closely as possible. The discretization is to be in such that the results converge to the true solution. However, too fine mesh will lead to extra computational effort. Fig. shows a finite element mesh of a continuum using triangular and quadrilateral elements. The assemblage of triangular elements in this case shows better representation of the continuum. The discretization process also shows that the more accurate representation is possible if the body is further subdivided into some finer mesh.

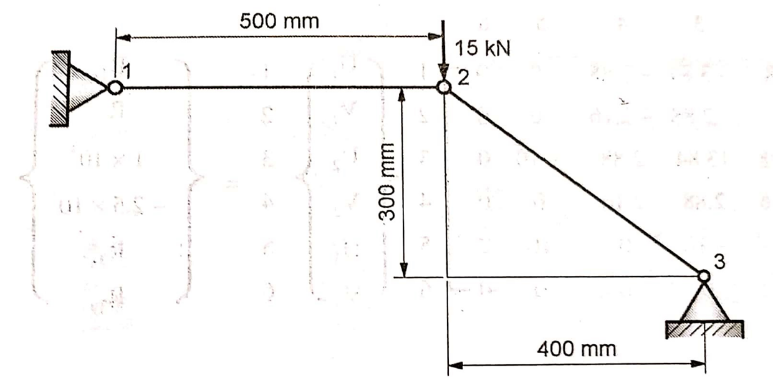
Q.10 The two bar truss is shown in fig. The modulus of elasticity for four bar material is 70 x 103 N/mm2 and cross sectional area of each element is 200 mm2. Determine

1) The element stiffness matrix

2) The global stiffness matrix

3) The nodal displacements

4) The stresses in each elements

5) The reaction forces

Solution

Given: E = 70 x 103 N/mm2 A = 200 mm2

l1 = 500 mm P2y = -15 kN

Discretization

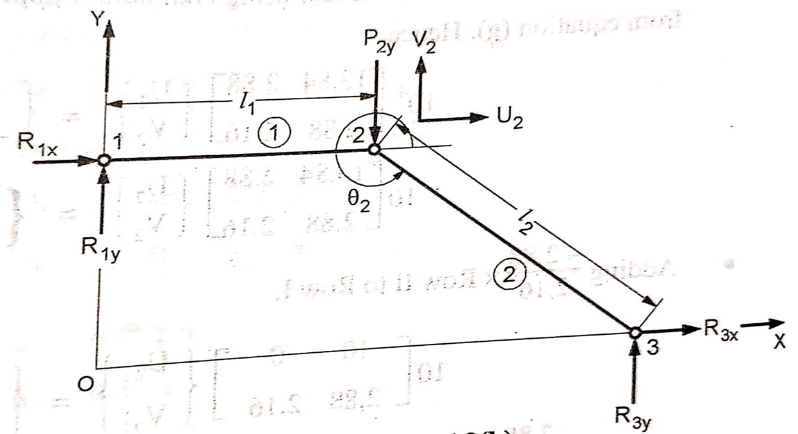
From fig,

Table below shows the element connectivity in the assembly

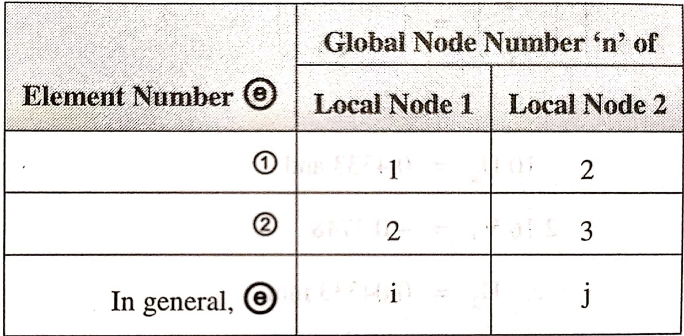
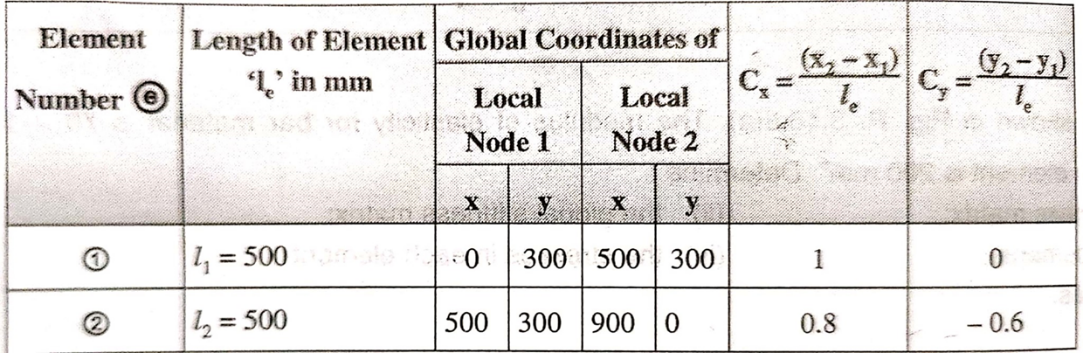
The values for Cx and Cy for all elements are

7. Nodal Displacements:

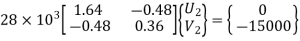
From the above equation, by solving for two unknowns

U2 = -0.7143 mm and V2 = -2.4405 mm

8. Reaction forces at support

28 x 103 [U1 –U2] = R1x

28 x 103 [0 –(-0.7143)] = R1x

R1x = 20000 N

R1y = 0

28 x 103 [-0.64U2 +0.48V2] = R3x

28 x 103 [-0.64 x (-0.7143) +0.48(-2.4405)] = R3x

R3x = -20000 N

28 x 103 [-0.48U2 -0.36V2] = R3y

28 x 103 [-0.48(-0.7143) -0.36(-2.4405)] = R3y

R3y = 15000 N

R1x =20000 N R1y = 0 R3x =-20000 N R3y=15000 N

10. Stresses in Elements

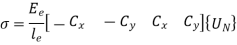
For element 1,

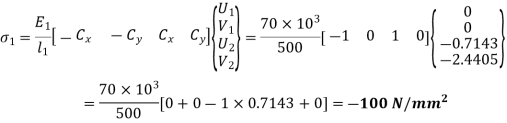
For element 2,

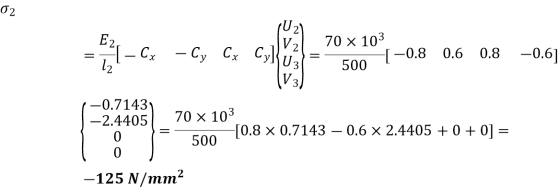
Q.11 Write down in detail, the steps to solve a 1D FEM problem.

Solution:

Step I: Discretization

Discretization is a process of dividing a body into finite number of elements.

Step II:Formulation of Global Load Vector

The elemental force vectors in the global coordinate system for all elements are assembled to form the global load vector {F} for the entire body.

The global Load Vector is given by,

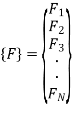
Where F1, F2, F3, …, FN are the loads acting at nodes 1,2,3,…,N respectively

Step III:Formulation of Global Nodal Displacement Vector

The global nodal displacement vector {UN} is formed for the entire body.

The global nodal displacement vector is given as

Where U1, U2, U3, … , UN are the displacements acting at nodes 1,2,3,…,N respectively

Step IV:Formulation of elemental stiffness matrices

After the body is discretized, the elemental stiffness matrix is formulated for all discretized elements.

Consider a one-dimensional rod element as shown in fig.

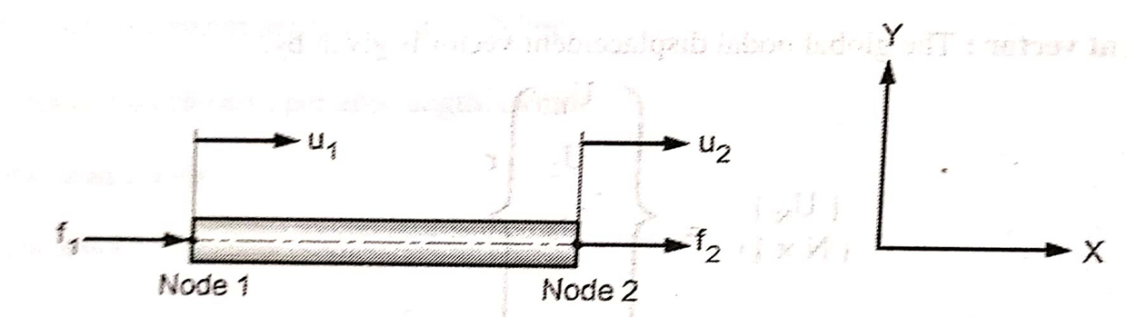
It has two nodes. Each node has one degree of freedom

Let

l = length of element

A = Cross-sectional area

E = modulus of Elasticity

f1 = Force acting at node 1

f2 = Force acting at node 2

u1 = displacement of node 1

u2 = displacement of node 2

Stiffness of rod element is

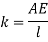
From fig,

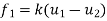
And

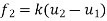
The above equations in matrix form can be written as

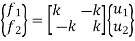
Where,

{f} = 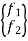= elemental force vector

[k] = = elemental stiffness matrix

{uN} = = elemental nodal displacement vector

Step V:Formulation of Global Stiffness Matrix

The global stiffness matrix is formed from the elemental nodal stiffness matrices.

Such as

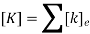
Step VI:Assembly of Global Stiffness – Nodal Displacement – Load Equations

The relationship between the global stiffness matrix [K], global nodal displacement vector {UN} and global load vector {f} is expressed as

{f} = [K]{UN}

This equation is called as Finite element equation.

If N is the total degree of freedom of the body.

Then dimension of

Global load vector is N x 1.

Global stiffness matrix is N x N.

Global displacement vector is N x 1.

Step VII:Specify boundary conditions

The specified boundary conditions are incorporated in equilibrium equation by using elimination approach or penalty approach.

Step VIII:Solution of Equations

After including the boundary conditions, the modified equations are solved for the unknown nodal displacements.

Step VIII:Computation of Elemental stresses and strains

Elemental strains are calculated from nodal displacements by

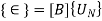
Where,

= Element strain

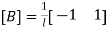= element strain-nodal displacement matrix

And from the strain calculated, stresses can be calculated as

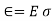
Where, 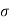= element stress

Sign Up