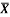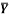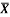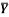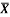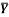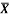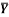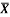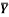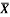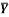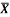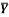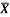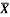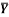Que. No | Question Statement | Que. No | Question Statement |
Centroid and C.G. | |||
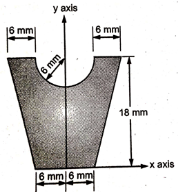
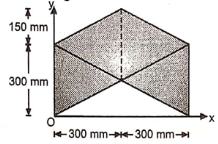
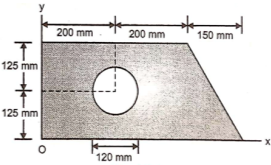
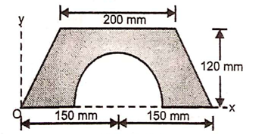
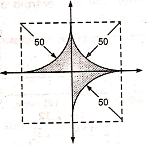
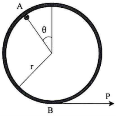
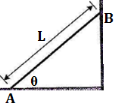
1 | Determine the Y coordinate of Centroid of the shaded area as shown in Figure. (May 13)
Ans:
| 2 |
Ans:
|
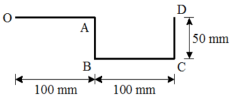
3 | A thin rod is bent into a shape OABCD as shown in Figure. Determine the Centroid of the bent rod with respect to origin O. (May 14) Ans:
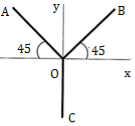
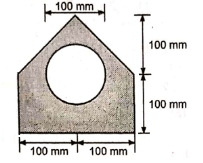
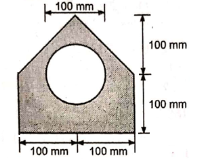
| 4 | Determine the coordinate of Centroid of the shaded area as shown in Fig. (Dec 14) Ans:
|
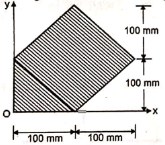
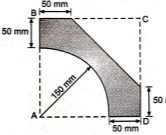
5 | Determine the X & Y coordinates of the Centroid with respect to the origin O of the shaded area as shown in Fig. (May 15) Ans:
| 6 | A semicircular area is cut from a trapezium as shown in Fig. Determine the Centroid of the shaded portion with respect to the origin. (Dec 15) Ans:
|
7 |
Ans:
| 8 | Determine the Y coordinate of Centroid of the shaded area as shown in Figure. (Dec 16)
Ans:
|
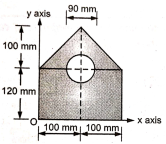
9 | Determine the position of centroid of the shaded area with respect to origin O as shown in Fig. (May 17)
Ans:
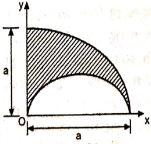
| 10 | Locate the centroid of the shaded area obtained by cutting a semicircle of diameter ‘a’ from the quadrant of a circle of radius ‘a’ as shown in Fig. with respect to origin O.
Ans:
|
11 |
Ans:
| 12 | Locate the centroid of the plane lamina as shown in figure. (Dec 18)
|
13 | Locate the centroid of the shaded area as shown in figure.
Ans:
| 14 | Locate the centroid of the shaded area as shown in figure.
|
15 | Find the value of distance ‘a’ So that centroid of the uniform lamina shown in Fig. remains at the centre of rectangle ABCD. (Dec-2002)
Ans: a = 21.58 cm
| 16 | Locate the centroid of the shaded area as shown in figure with respect to given axes. Ans:
|
Moment of Inertia | |||
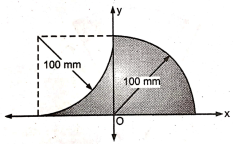
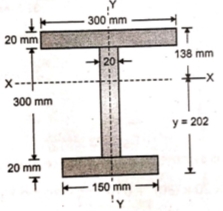
1 | Determine the M.I. of the ‘I’ section about x and y axis passing through its C.G. as shown in figure.
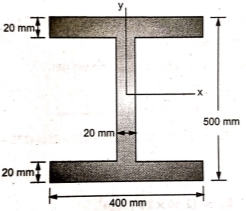
| 2 | Determine the M.I. of the Composite section about x and y axis passing through its C.G. as shown in figure.
|
3 | Determine the M.I. of the ‘I’ section about its Centroidal xx and yy axis. The particulars are: Top Flange - 300 mm x 20 mm Web -20m x 300 mm Bottom flange -150 mm x20 mm
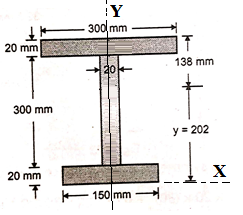
| 4 | Determine the M.I. of the ‘I’ section about xx and yy axis as shown in figure. The particulars are: Top Flange - 300 mm x 20 mm Web -20m x 300 mm Bottom flange -150 mm x20 mm
|
5 | Determine the MI of the shaded area as shown in Figure about X axis passing through its bottom edge. | 6 | Determine the MI of the shaded area as shown in Figure about Centroid X and Y axis.
|
Friction | |||
1 |
| 2 |
|
3 |
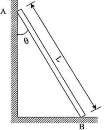
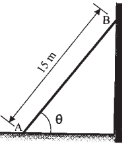
| 4 | The 15 m ladder has a uniform weight of 80 N. It rests against smooth vertical wall at B and horizontal floor at A. If the coefficient of static friction between ladder and floor at A is μs = 0.4, determine the smallest angle θ with vertical wall at which the ladder will slip. |
5 |
| 6 |
|
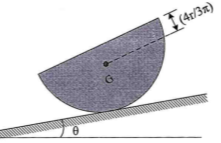
7 | The homogeneous semi-cylinder has a mass m and mass centre at G as shown in Fig. Determine the largest angle θ of the inclined plane upon which it rest so that it does not slip down the plane. The coefficient of static friction between the plane and cylinder is 0.3.
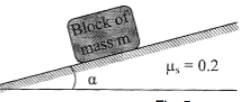
| 8 | A block of mass m rest on a frictional plane which makes an angle α with the horizontal as shown in Fig. If the coefficient of friction between the block and the frictional plane is 0.2, determine the angle α for limiting condition.
|
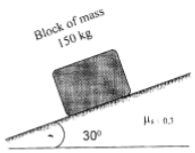
9 | Determine the range of P for the limiting equilibrium of block B of mass 150 kg rest on an inclined plane as shown in Fig.
μs = 0.3
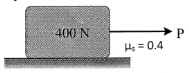
| 10 | A 400 N block is resting on a rough horizontal surface as shown in Fig. for which the coefficient of friction is 0.4. Determine the force P required to cause motion if applied to the block horizontally. What minimum force is required to start motion?
|
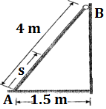
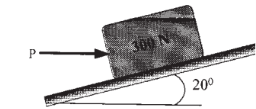
11 | Determine the horizontal force P needed to just moving the 300 N block up the plane. Take μs= 0.3 and refer Fig.
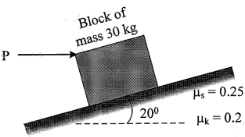
| 12 | Determine the horizontal force P needed to just start moving the 30 kg block up the plane as shown in fig. Take μs = 0.25 and μk = 0.25
|
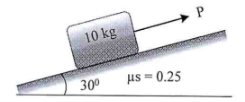
13 | A block of mass 10 kg rests on an inclined plane as shown in Fig. If the coefficient of static friction between the block and plane is μs = 0.25, determine the maximum force P to maintain equilibrium.
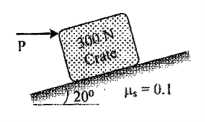
| 14 | Determine the horizontal force P needed to just start moving the 300 N crate up the plane as shown in Fig. Take µs = 0.1.
|
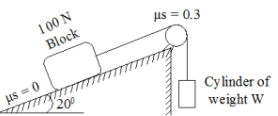
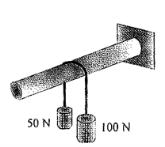
15 | Determine the range of cylinder weight W as shown in Fig. 6 b for which the system is in equilibrium. The coefficient of friction between cord and cylindrical support surface is 0.3 and that between100 N block and the incline surface is zero.
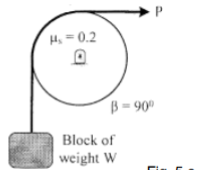
| 16 | Determine the range of P for the equilibrium of block of weight W as shown in Fig. The coefficient of friction between rope and pulley is 0.2.
|
17 | A cable is passing over the disc of belt friction apparatus at a lap angle 180° as shown in Fig. If the weight of block is 500 N, Determine the range of force P to mainntain equilibrium.
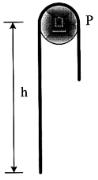
| 18 | A chain having a weight of 1 .5 N/m and total length of 10 m is suspended over a peg P as shown in Fig. If the coefficient of static friction hetwen the peg and cord is μs = 0.25, determine the largest length h which one side of the suspended cord can have without causing motion. Neglect the size of peg.
|
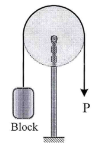
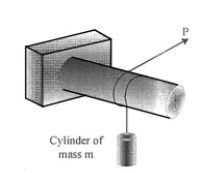
19 | Determine the minimum coefficient of static friction between the rope and the fixed shaft as shown in Fig. 6 will prevent the unbalanced cylinder from moving.
| 20 | A force P = mg/6 is required to lower the cylinder with the cord making 1.25 turns around t.he fixed shaft. Determine the coefficient of friction between the cord and the shaft. Refer Fig.
|
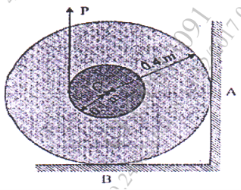
21 | The spool has a mass of 200 kg and rest against the wall and on the beam shown in Fig. If the coefficient of static friction at B is μB = 0.3 and the wall is smooth, determine the friction force developed at B when the vertical force applied to the cable is P = 800 N.
| 22 |
|