UNIT - 2

Geometric Design of Highways

Q1)          The design speed on a road is 60 kmph. Assuming the driver reaction time to be 2.5 seconds and coefficient of friction as 0.35, calculate the required SSD for two-way traffic on a single lane road.

Ans 1):

SSD = 0.278Vt +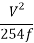

Where, V = 60 kmph

t = 2.5 sec

f = 0.35

Therefore, SSD = (0.278 x 60 x 2.5) + = 41.7 + 40.49 = 82.19 m

But, since traffic is two-way

SSD = 2 x 82.19 = 164.38 m

Q2)          The co-efficient of friction in the longitudinal direction of a highway is estimated to be 0.396. Calculate braking distance for a car moving at a speed of 65 km/hr.

Ans 2):

Braking distance =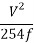

Where, V = 65 kmph

f = 0.396

Therefore, SSD = 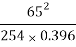= 42 m

Q3)          A road is having a horizontal curve of 400m radius on which a super-elevation of 0.07 is provided. Calculate the coefficient of lateral friction mobilized on a curve for a vehicle travelling with a speed of 100 kmph.

Ans 3):

Radius of curve R =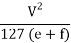

e + f =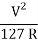

f = 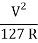– e = 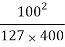– 0.07 = 0.13

Q4)          Discuss about the importance of Drainage in Highways.

Ans 4):

The importance of drainage is one of the most important aspects for location and design of highway because of following reasons: 

• To prevent sub-grade failure: Soil sub-grade excess moisture reducing the stability of pavement which leads to sub-grade failure. 
• To prevent reduction in strength of pavement material: The strength of pavement material like stabilized soil and WBM (water bound macadam) is reduced. 
• To prevent frost action: In flexible pavement, the formation of waves and corrugation take place due to poor drainage.
• Volume changes: Volume of sub-grade is change especially in clayey soils due to variation in moisture content. This sometimes leads to pavement failure.
• Prevent mud pumping failure: Mud pumping is due to presence of water in sub-grade soil especially in rigid pavement.
• To prevent shoulders and pavement edge: Excess water on shoulders and pavement edge cause considerable damage.
• Prevent slope failure: Excess moisture causes increase in weight and thus increases in stress and simultaneously reduction in strength of soil mass which result into failure of earth slopes and embankment foundations.
• Prevent erosion of soil: Due to surface water, erosion of soil from top of road and slope of embankment. Thus drainage is the important factors governing the highway design and construction.

Q5)          The design speed for a two-lane road is 80 kmph. When design vehicle with a wheel base of 6.6m is negotiating a horizontal curve on the road, the off-tracking is measured as 0.096m. Calculate the extra-widening of the carriageway.

Ans 5):

Off-tracking = = 0.096

Therefore, R = = 226.875 m

Extra-widening We = 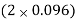+ 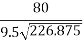= 0.752 m

Q6)          Discuss the Optimum Road Length using Nagpur Road Plan.

Ans 6):

NH + SH + MDR = [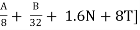 + D – R

ODR + VR = [0.32V + 0.8Q + 1.6P + 3.2S] + D

Here, NH = National Highway

SH = State Highway

MDR = Major District Roads

ODR = Other District Roads

VR = Village Roads

A = agricultural area, km2

B = non-agricultural area, km2

N = number of towns & villages with population range 2001-5000

T = number of towns & villages with population > 5000

D = development allowance of 15% for next 20 years

R = existing length of railway track

V = number of villages with population 500 or less

Q = number of villages with population 501-1000

P = number of villages with population 1001-2000

S = number of villages with population 2001-5000

Q7)          State the IRC Recommendations for Ruling Design Speed for various roads.

Ans 7):

IRC Recommendations for Ruling Design Speed

Q8)          What do you understand by Setback Distance?

Ans 8):

The distance from the centre line of the entire road to nearest obstruction on the inner side of the road to have proper sight distance over the entire length of curve is called Setback Distance. It depends upon the following factors:

a)     Required sight distance, S

b)    Radius of horizontal curve, R

c)     Length of curve, L

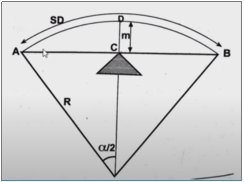
Single Lane Road

Case 1: L ≥ S

We know that, arc length = R

Therefore, S = R

Further,  = S/R (in radians)

/2 = S/2R (in radians)

We can also say /2 = 180S/ 2𝝿R (in degrees)

Therefore, set-back distance m = CF = OF – OC

Hence, m = R – R cos (/2)

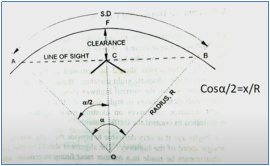
Case 2: L < S

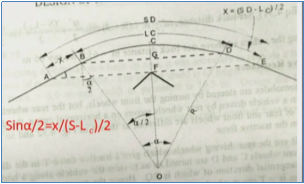
Set-back distance m = FC = FG + GC

Here, GC = R – R cos (/2)

FG = sin (/2)

Therefore, m = [R – R cos (/2)] + [ sin (/2)]

Multi Lane Road

Case 1: L ≥ S

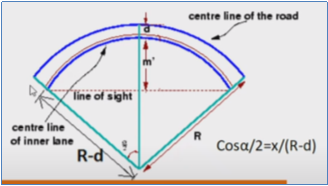
d = distance between centre line of the road and centre line of the inside lane

Therefore, S = R

Hence, m’ = R – (R-d) cos (/2)

Where, /2 = 180S/ 2𝝿(R-d) (in degrees)

Case 2: L < S

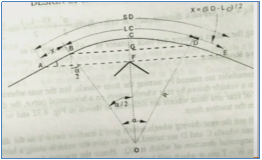
Set-back distance m’ = FC = FG + GC

Here, GC = R – (R-d) cos (/2)

FG = 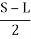sin (/2)

Therefore, m = [R – (R-d) cos (/2)] + [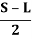 sin (/2)]

Q9)          Discuss the Optimum Road Length using Bombay Road Plan.

Ans 9):

NH = [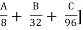 + [32K + 8M] + D

NH + SH = [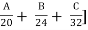 + [48K + 24M + 11.2N + 1.6P] + D

NH + SH + MDR = [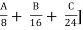 + [48K + 24M + 11.2N + 9.6P + 4.6Q + 2.4R] + D

NH + SH + MDR + ODR = [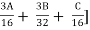 + [48K + 24M + 11.2N + 9.6P + 4.6Q + 2.4R] + D

NH + SH + MDR + ODR + VR = [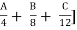 + [48K + 24M + 11.2N + 9.6P + 12.8Q + 5.9R + 1.6S + 0.64T + 0.2V] + D

Here, NH = National Highway

SH = State Highway

MDR = Major District Roads

ODR = Other District Roads

VR = Village Roads

A = developed & agricultural area, km2

B = semi-developed area, km2

C = undeveloped area, km2

K = number of towns with population > 100000

M = number of towns with population 50000 - 100000

N = number of towns with population 20000 - 50000

P = number of towns with population 10000 - 20000

Q = number of towns with population 5000 - 10000

R = number of towns with population 2000 - 5000

S = number of towns with population 1000 - 2000

T = number of towns with population 500 - 1000

V = number of towns with population 500 or less

D = development allowance of 5% for next 20 years

Q10)      Discuss the Optimum Road Length using Maximum Utility System.

Ans 10):

Maximum Utility System for Optimum Road Length

Various studies are made to assess the road length requirements, including economic studies, financial studies, traffic or road use studies and engineering studies.

However, one of the most commonly used method for deciding the Optimum Road Length is the Maximum Utility System. In this system, the optimum road length for an area is calculated on the basis of maximum utility per unit length of the road. This system is also known as Saturation System. Factors for obtaining the utility per unit length of road are:

1. Population served by the road
2. Agricultural & Industrial productivity served by the road network

A utility unit is assigned to towns/ villages on the basis of population, as given in the table below:

This is followed by phasing of the road development plan by fixing the priorities for construction of different road links.