Unit - 3
Centroids and Moments of Inertia
Q1) Determine the second moment of area about the neutral axis of the I-section shown in Figure.
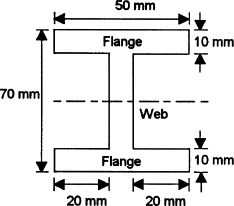
A1)
We can determine the second moment of area for such a section by determining the second moment of area for the entire rectangle containing the section and then subtracting the second moments of area for the rectangular pieces ‘missing’
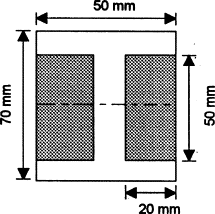
Thus for the rectangle containing the entire section, the second moment of area is given by I = bd3/12 = (50 × 703)/12 = 1.43 × 106mm4. Each of the ‘missing’ rectangles will have a second moment of area of (20 × 503)/12 = 0.21 × 106 mm4. Thus the second moment of area of the I-section is 1.43 × 106 − 2 × 0.21 × 106 = 1.01 × 106mm4
Q2) Determine moment of Inertia for  section about x & y axis as shown in figure.
section about x & y axis as shown in figure.
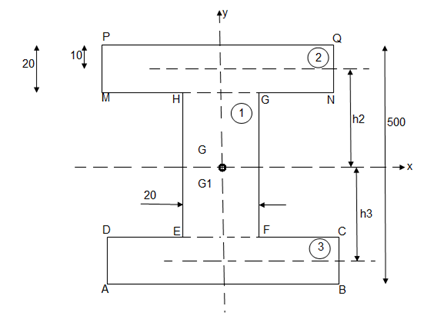
A2)
M.I. If this rectangle about xx and yy axis will be,     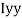  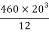 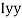 |  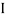 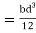 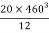 = 106666666.7 mm4 Consider rectangle ABCD area ③ 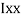   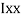  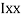 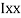 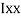  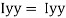  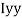 = 213.64 
|
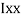 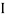 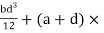  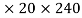 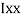 |
Q3) Determine the moment of inertia of shaded area as shown in figure about its centroid as axis.
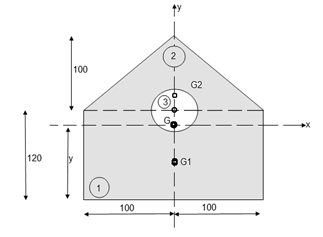
A3)
As this figure is symmetrical about
Y axis
X = 100 mm
Y = 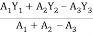
Where,
Area ① = rectangle
Area ② = triangle
Area ③ = circle
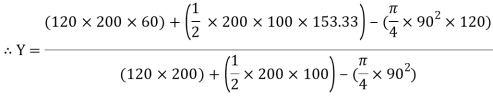
Y = 79.95 mm
 to find M.I. Of shaded portion , let G is the centroid of shaded area which is at y = 79.95 mm from base.
to find M.I. Of shaded portion , let G is the centroid of shaded area which is at y = 79.95 mm from base.
 of shaded portion @ x-x axis passing through its centroid G will be,
of shaded portion @ x-x axis passing through its centroid G will be,
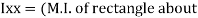 x-x) +
x-x) +
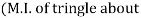 x-x) –
x-x) –
 x-x axis)
x-x axis)
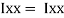 1 +
1 +  2
2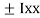 3
3
= ( G1 + A1h12) +
G1 + A1h12) +  G2 + A2h22) -
G2 + A2h22) -  G3 + A3h32)
G3 + A3h32)
=  +
+ 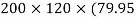 -60
-60 ] +
] +
 +
+ 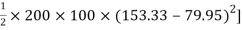 –
–
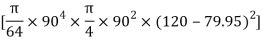
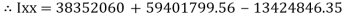
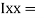 84329013.21 mm4
84329013.21 mm4
 of shaded portion about y-y axis passing through its centroid G will be,
of shaded portion about y-y axis passing through its centroid G will be,
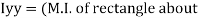 y-y) +
y-y) +
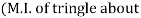 y-y axis) –
y-y axis) –
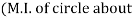 y-yaxis)
y-yaxis)
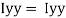 1 +
1 + 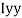 2
2 3
3
= 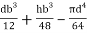
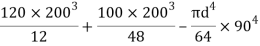
= 80000000 + 16666666.67 – 3220623.34
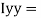 93446043.33 mm4
93446043.33 mm4
Q4) A body of weight 50 N is along rough horizontal plane A pull of 18 N acting at an angle of 140 with the horizontal find coefficient of static friction.
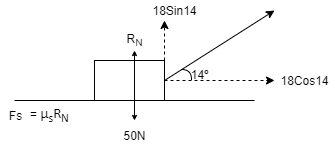
A4)
Considering the equilibrium of block
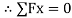
 18 Cos 14 – Fs = 0
18 Cos 14 – Fs = 0
 Fs = 17.46 N
Fs = 17.46 N
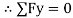
RN + 18 Sin 14 – 50 = 0
RN = 45.64 N
As Fs = 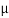 S RN
S RN
17.46 = 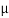 S
S  45.64
45.64
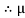 S = 0.386
S = 0.386
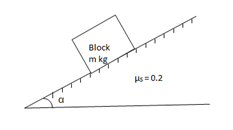
Q5) A block of mass m rests on frictional plane which makes an angle 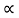 with horizontal as shown if the coeff. Of friction between the block & frictional plane is 0.2, determine angle
with horizontal as shown if the coeff. Of friction between the block & frictional plane is 0.2, determine angle  for limiting friction.
for limiting friction.
A5)
For limiting friction
Tan  tan
tan  S =
S = 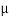 S
S
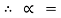 tan-1
tan-1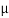 S
S
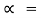 tan-1
tan-1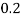
 11.310
11.310
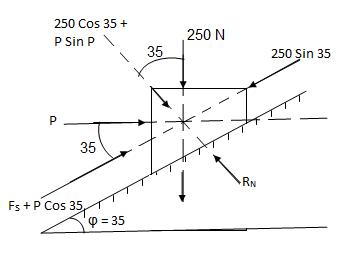
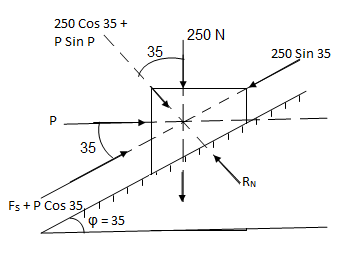
Q6) Determine whether the block shown is in equilibrium and find the magnitude and direction of friction force when 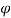 = 350 and P = 100 N
= 350 and P = 100 N
A6)
Let us select inclined plane as x-x axis & perpendicular to plane as y-y axis
Let Fs = static frictional force which is required to maintain equilibrium.
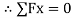 -------- resolving force along x-axis
-------- resolving force along x-axis
 Fs + 100 Cos 35 – 250 Sin 35 = 0
Fs + 100 Cos 35 – 250 Sin 35 = 0
 Fs – 61.48 = 0
Fs – 61.48 = 0
 Fs = 61.48 N ----- frictional force
Fs = 61.48 N ----- frictional force
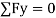 -------- resolving force along y-axis
-------- resolving force along y-axis
 -(250 Cos 35 + P Sin 35) + RN = 0
-(250 Cos 35 + P Sin 35) + RN = 0
 -250 Cos 35 – 100 Sin 35 + RN = 0
-250 Cos 35 – 100 Sin 35 + RN = 0
-262.15 + RN = 0
 RN = 262.15 N -------- normal reaction
RN = 262.15 N -------- normal reaction
Maximum frictional force can be developed is given by
Fs max = 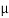 S
S RN = 0.3
RN = 0.3  262.15
262.15
Fs max = 78.65 N
As frictional force required to maintain equilibrium (61.48 N) is less than max. Frictional force,
 Equilibrium will be maintained
Equilibrium will be maintained
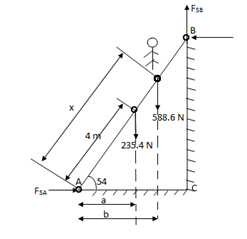
Q7) Uniform ladder AB has a length of 8 m and mass 24 kg end A is on horizontal floor and end B rests against vertical wall. A man of mass of 60 kg has to climb this ladder. At what position from the base, will be induce the slipping of ladder.
A7)
Take 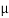 S = 0.34 at all contact surface.
S = 0.34 at all contact surface.
Weight of man = 60 9.81 =588.6 N
9.81 =588.6 N
Weight of ladder 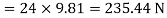
AB = 8 m
Impending motion
 Ac = 8 Cos 54
Ac = 8 Cos 54
 BC = 8 Sin 54
BC = 8 Sin 54
 ɑ = 2.35 m
ɑ = 2.35 m
 b = x Cos 54
b = x Cos 54
 FSA =
FSA =  S
S  RNA
RNA
 FSB =
FSB = 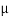 S
S  RNB
RNB
Considering the equilibrium of ladder
 FX = 0
FX = 0
  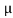  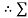         |
 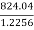

From eqn …..1
RNB = 0.34 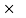

|
Taking moment about point A,
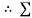 MA = 0
MA = 0
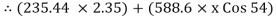
 SB
SB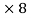 Cos 54) – (RNB
Cos 54) – (RNB 8 Sin 54) = 0
8 Sin 54) = 0
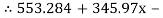 (
( S
S  RNB
RNB  4.7) – (6.47 RNB) = 0
4.7) – (6.47 RNB) = 0
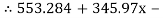 1.598 RNB – 6.47 RNB = 0
1.598 RNB – 6.47 RNB = 0
 345.97x – 8.068 RNB = 553.284
345.97x – 8.068 RNB = 553.284
 345.97x – 8.068
345.97x – 8.068  251.14 = 553.284
251.14 = 553.284
 345.97x = 1472.913
345.97x = 1472.913
X = 4.257 m
At X = 4.257 m from point A, along the ladder, man can climb without slipping.
Beyond this distance, ladder will be slipping.
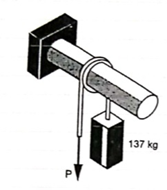
Q8) A 137 kg block is supported by a rope which Is wrapped 1.5 times around a horizontal Rod knowing that coeff. Of static friction Between rope and rod is 0.15, determine the range of values of P for which Equilibrium is maintained.
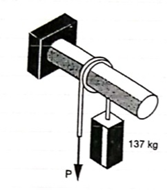
A8)
Weight of block = 
Angle of contact = LAP Angle
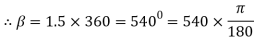
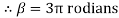
A) Case I: when P > 1343.97 N
Force P tends to move the rope down ward and block moves upward. Thus the part rope on which force P is acting is height side and rope to which block is attached is slack side.
 =
=  =
= 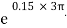
 P = 5525.34 N
P = 5525.34 N
B) Case II: when P < 1343.97 N
 force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward.
force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward.
 Rope side to which block is attached is tight side and another side is slack side.
Rope side to which block is attached is tight side and another side is slack side.
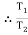 =
=  =
= 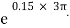
 P = 326.92 N
P = 326.92 N
 range of P for equilibrium is 326.92 N
range of P for equilibrium is 326.92 N 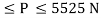
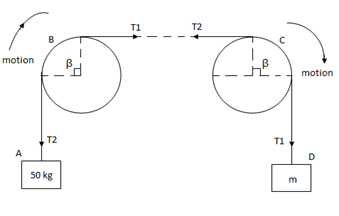
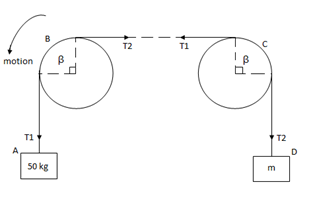
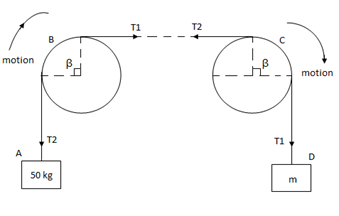
Q9) Two cylinders are connected by a rope that passes Over two fixed rods as shown. Knowing that the Coefficient of static friction between the rope and the rods is 0.40. Determine the range of the mass m of cylinder D for which equilibrium is maintained.
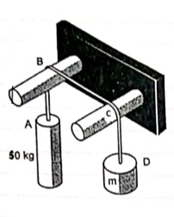
A9)
Weight of cylinder = 50  9.81 = 490.5 N
9.81 = 490.5 N
Lap angle = 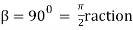
 S = 0.40
S = 0.40
A) Case I:
Weight of cylinder A > weight of cylinder B.
In this case cylinder A will tends to move downward while B will tends to move upward
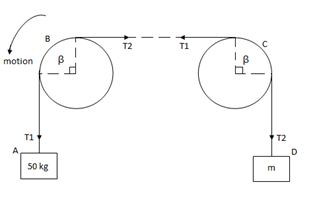
Consider part AB of the Rope as AB rope is moving down,
Tension in hight side T1 = 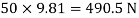
Tension in slack side = T2 = unknown.
 =
= 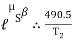 =
=  = 1.874
= 1.874
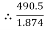 = T2
= T2
 T2 = 261.74 N
T2 = 261.74 N
Consider part CD, of the rope. As rope CD is moving upward,
Tension in tight side T1 = T2 of rope AB
Tension in tight side, T1 = 261.74 N
Tension in slack side = T2 = (m  9.81)
9.81)
 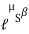 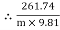 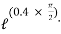 |   |
B) Case II:
Weight of cylinder A < weight of cylinder B
In this case cylinder a will tends to move upward while cylinder B will tends to move downward
Consider part AB of the rope moving upwards
Tension in slack side = side A = 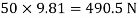
  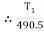  | 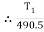 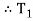 |
Consider part CD of rope, Rope CD is moving downwards
Tension in tight side = T1 = (m 9.81) N
9.81) N
Tension in slack side = T2 = T1 of rope AB = 919.197 N
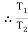  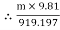  | 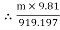  |
Range of mass m for equilibrium to be maintained is
14.23 kg 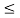 m
m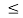 175.59 kg
175.59 kg
Q10) A Force P = mg/6 is required to lower the cylinder with card making 1.25 turns around the fixed shaft. Determine the coeff. Of friction “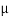 S” between the card and the shaft
S” between the card and the shaft
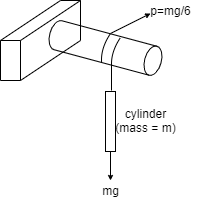
A10)
Refer the figure
Lap angle
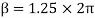
= 2.5 radians
radians
For flat belt,
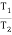 =
= 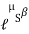
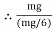 =
= 
 6
6 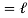
 1.79 =
1.79 = 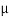 S
S 2.5
2.5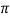
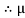 S = 0.23
S = 0.23
Q11) Determine the range of P for the equilibrium of block of weight W as shown in fig. The coeff. Of friction between rope and pulley is 0.2
A11)
Case I: when P is max.
 =
= 
 =
= 
 Pmax = 1.369 w
Pmax = 1.369 w
Case II: when P is min.
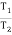 =
= 
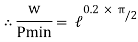
 Pmin = 0.73 w
Pmin = 0.73 w
For equilibrium P must be between 0.73  P
P  1.369 w
1.369 w
Unit - 3
Centroids and Moments of Inertia
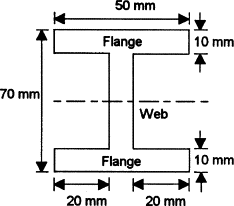
Q1) Determine the second moment of area about the neutral axis of the I-section shown in Figure.
A1)
We can determine the second moment of area for such a section by determining the second moment of area for the entire rectangle containing the section and then subtracting the second moments of area for the rectangular pieces ‘missing’
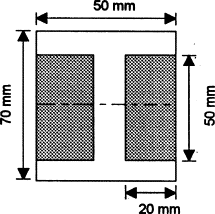
Thus for the rectangle containing the entire section, the second moment of area is given by I = bd3/12 = (50 × 703)/12 = 1.43 × 106mm4. Each of the ‘missing’ rectangles will have a second moment of area of (20 × 503)/12 = 0.21 × 106 mm4. Thus the second moment of area of the I-section is 1.43 × 106 − 2 × 0.21 × 106 = 1.01 × 106mm4
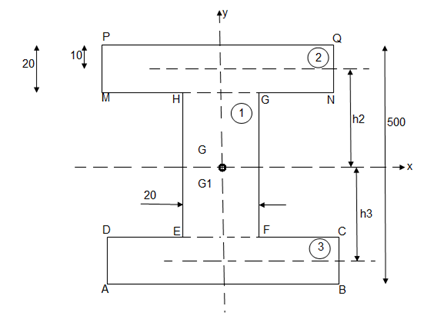
Q2) Determine moment of Inertia for 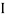 section about x & y axis as shown in figure.
section about x & y axis as shown in figure.
A2)
M.I. If this rectangle about xx and yy axis will be,  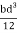   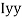   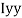 | 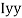 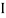  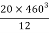 = 106666666.7 mm4 Consider rectangle ABCD area ③ 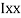 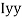  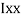 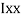   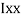   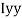 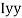 = 213.64 
|
 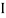  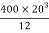  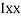 |
Q3) Determine the moment of inertia of shaded area as shown in figure about its centroid as axis.
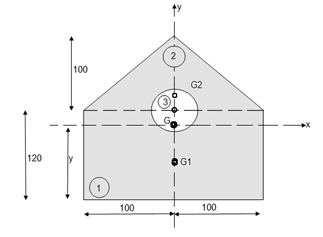
A3)
As this figure is symmetrical about
Y axis
X = 100 mm
Y = 
Where,
Area ① = rectangle
Area ② = triangle
Area ③ = circle
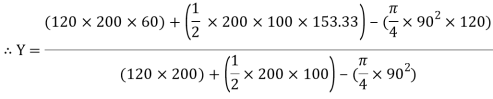
Y = 79.95 mm
 to find M.I. Of shaded portion , let G is the centroid of shaded area which is at y = 79.95 mm from base.
to find M.I. Of shaded portion , let G is the centroid of shaded area which is at y = 79.95 mm from base.
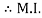 of shaded portion @ x-x axis passing through its centroid G will be,
of shaded portion @ x-x axis passing through its centroid G will be,
 x-x) +
x-x) +
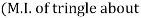 x-x) –
x-x) –
 x-x axis)
x-x axis)
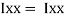 1 +
1 + 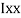 2
2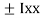 3
3
= (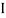 G1 + A1h12) +
G1 + A1h12) + 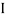 G2 + A2h22) -
G2 + A2h22) - 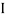 G3 + A3h32)
G3 + A3h32)
= 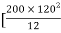 +
+  -60
-60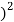 ] +
] +
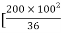 +
+ 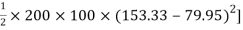 –
–
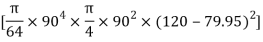
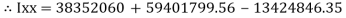
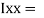 84329013.21 mm4
84329013.21 mm4
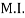 of shaded portion about y-y axis passing through its centroid G will be,
of shaded portion about y-y axis passing through its centroid G will be,
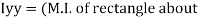 y-y) +
y-y) +
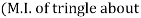 y-y axis) –
y-y axis) –
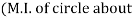 y-yaxis)
y-yaxis)
 1 +
1 +  2
2 3
3
= 
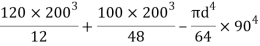
= 80000000 + 16666666.67 – 3220623.34
 93446043.33 mm4
93446043.33 mm4
Q4) A body of weight 50 N is along rough horizontal plane A pull of 18 N acting at an angle of 140 with the horizontal find coefficient of static friction.
A4)
Considering the equilibrium of block
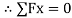
 18 Cos 14 – Fs = 0
18 Cos 14 – Fs = 0
 Fs = 17.46 N
Fs = 17.46 N
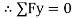
RN + 18 Sin 14 – 50 = 0
RN = 45.64 N
As Fs = 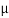 S RN
S RN
17.46 = 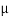 S
S  45.64
45.64
 S = 0.386
S = 0.386
Q5) A block of mass m rests on frictional plane which makes an angle 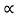 with horizontal as shown if the coeff. Of friction between the block & frictional plane is 0.2, determine angle
with horizontal as shown if the coeff. Of friction between the block & frictional plane is 0.2, determine angle 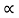 for limiting friction.
for limiting friction.
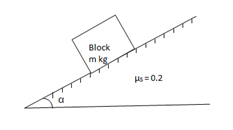
A5)
For limiting friction
Tan 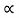 tan
tan  S =
S = 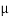 S
S
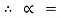 tan-1
tan-1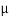 S
S
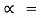 tan-1
tan-1
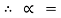 11.310
11.310
Q6) Determine whether the block shown is in equilibrium and find the magnitude and direction of friction force when 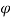 = 350 and P = 100 N
= 350 and P = 100 N
A6)
Let us select inclined plane as x-x axis & perpendicular to plane as y-y axis
Let Fs = static frictional force which is required to maintain equilibrium.
 -------- resolving force along x-axis
-------- resolving force along x-axis
 Fs + 100 Cos 35 – 250 Sin 35 = 0
Fs + 100 Cos 35 – 250 Sin 35 = 0
 Fs – 61.48 = 0
Fs – 61.48 = 0
 Fs = 61.48 N ----- frictional force
Fs = 61.48 N ----- frictional force
 -------- resolving force along y-axis
-------- resolving force along y-axis
 -(250 Cos 35 + P Sin 35) + RN = 0
-(250 Cos 35 + P Sin 35) + RN = 0
 -250 Cos 35 – 100 Sin 35 + RN = 0
-250 Cos 35 – 100 Sin 35 + RN = 0
-262.15 + RN = 0
 RN = 262.15 N -------- normal reaction
RN = 262.15 N -------- normal reaction
Maximum frictional force can be developed is given by
Fs max = 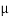 S
S RN = 0.3
RN = 0.3  262.15
262.15
Fs max = 78.65 N
As frictional force required to maintain equilibrium (61.48 N) is less than max. Frictional force,
 Equilibrium will be maintained
Equilibrium will be maintained
Q7) Uniform ladder AB has a length of 8 m and mass 24 kg end A is on horizontal floor and end B rests against vertical wall. A man of mass of 60 kg has to climb this ladder. At what position from the base, will be induce the slipping of ladder.
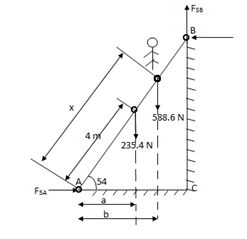
A7)
Take  S = 0.34 at all contact surface.
S = 0.34 at all contact surface.
Weight of man = 60 9.81 =588.6 N
9.81 =588.6 N
Weight of ladder 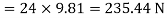
AB = 8 m
Impending motion
 Ac = 8 Cos 54
Ac = 8 Cos 54
 BC = 8 Sin 54
BC = 8 Sin 54
 ɑ = 2.35 m
ɑ = 2.35 m
 b = x Cos 54
b = x Cos 54
 FSA =
FSA = 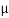 S
S  RNA
RNA
 FSB =
FSB = 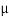 S
S  RNB
RNB
Considering the equilibrium of ladder
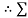 FX = 0
FX = 0
    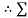   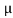      |
 

From eqn …..1
RNB = 0.34 

|
Taking moment about point A,
 MA = 0
MA = 0
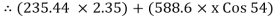
 SB
SB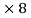 Cos 54) – (RNB
Cos 54) – (RNB 8 Sin 54) = 0
8 Sin 54) = 0
 (
(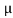 S
S 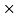 RNB
RNB  4.7) – (6.47 RNB) = 0
4.7) – (6.47 RNB) = 0
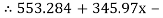 1.598 RNB – 6.47 RNB = 0
1.598 RNB – 6.47 RNB = 0
 345.97x – 8.068 RNB = 553.284
345.97x – 8.068 RNB = 553.284
 345.97x – 8.068
345.97x – 8.068 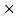 251.14 = 553.284
251.14 = 553.284
 345.97x = 1472.913
345.97x = 1472.913
X = 4.257 m
At X = 4.257 m from point A, along the ladder, man can climb without slipping.
Beyond this distance, ladder will be slipping.
Q8) A 137 kg block is supported by a rope which Is wrapped 1.5 times around a horizontal Rod knowing that coeff. Of static friction Between rope and rod is 0.15, determine the range of values of P for which Equilibrium is maintained.
A8)
Weight of block = 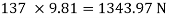
Angle of contact = LAP Angle
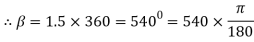

A) Case I: when P > 1343.97 N
Force P tends to move the rope down ward and block moves upward. Thus the part rope on which force P is acting is height side and rope to which block is attached is slack side.
 =
=  =
= 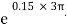
 P = 5525.34 N
P = 5525.34 N
B) Case II: when P < 1343.97 N
 force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward.
force P is less than 1343.97 N, so block will move down ward & the side rope on which P acts will move upward.
 Rope side to which block is attached is tight side and another side is slack side.
Rope side to which block is attached is tight side and another side is slack side.
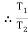 =
= 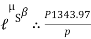 =
= 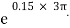
 P = 326.92 N
P = 326.92 N
 range of P for equilibrium is 326.92 N
range of P for equilibrium is 326.92 N 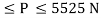
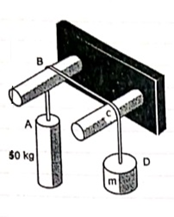
Q9) Two cylinders are connected by a rope that passes Over two fixed rods as shown. Knowing that the Coefficient of static friction between the rope and the rods is 0.40. Determine the range of the mass m of cylinder D for which equilibrium is maintained.
A9)
Weight of cylinder = 50  9.81 = 490.5 N
9.81 = 490.5 N
Lap angle = 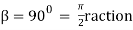
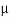 S = 0.40
S = 0.40
A) Case I:
Weight of cylinder A > weight of cylinder B.
In this case cylinder A will tends to move downward while B will tends to move upward
Consider part AB of the Rope as AB rope is moving down,
Tension in hight side T1 = 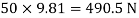
Tension in slack side = T2 = unknown.
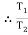 =
=  =
= 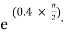 = 1.874
= 1.874
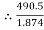 = T2
= T2
 T2 = 261.74 N
T2 = 261.74 N
Consider part CD, of the rope. As rope CD is moving upward,
Tension in tight side T1 = T2 of rope AB
Tension in tight side, T1 = 261.74 N
Tension in slack side = T2 = (m  9.81)
9.81)
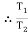   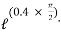 | 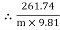  |
B) Case II:
Weight of cylinder A < weight of cylinder B
In this case cylinder a will tends to move upward while cylinder B will tends to move downward
Consider part AB of the rope moving upwards
Tension in slack side = side A = 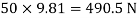
  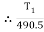 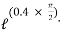 |  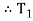 |
Consider part CD of rope, Rope CD is moving downwards
Tension in tight side = T1 = (m 9.81) N
9.81) N
Tension in slack side = T2 = T1 of rope AB = 919.197 N
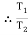 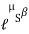   | 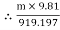  |
Range of mass m for equilibrium to be maintained is
14.23 kg 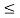 m
m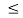 175.59 kg
175.59 kg
Q10) A Force P = mg/6 is required to lower the cylinder with card making 1.25 turns around the fixed shaft. Determine the coeff. Of friction “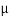 S” between the card and the shaft
S” between the card and the shaft
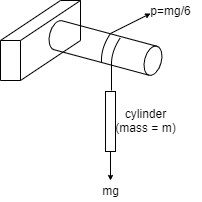
A10)
Refer the figure
Lap angle
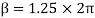
= 2.5 radians
radians
For flat belt,
 =
= 
 =
= 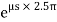
 6
6 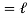
 1.79 =
1.79 = 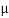 S
S 2.5
2.5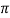
 S = 0.23
S = 0.23
Q11) Determine the range of P for the equilibrium of block of weight W as shown in fig. The coeff. Of friction between rope and pulley is 0.2
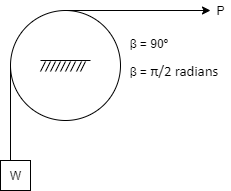
A11)
Case I: when P is max.
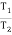 =
= 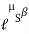
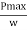 =
= 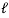
 Pmax = 1.369 w
Pmax = 1.369 w
Case II: when P is min.
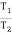 =
= 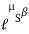
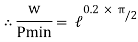
 Pmin = 0.73 w
Pmin = 0.73 w
For equilibrium P must be between 0.73  P
P 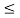 1.369 w
1.369 w