Unit - 1
Sets, Relation and Function
Q1) Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).
A1)
Using the formula n(A ∪ B) = n(A) + n(B) - n(A ∩ B).
Then n(A ∩ B) = n(A) + n(B) - n(A ∪ B)
= 20 + 28 - 36
= 48 - 36
= 12
Q2) In a competition, a school awarded medals in different categories. 36 medals in dance, 12 medals in dramatics and 18 medals in music. If these medals went to a total of 45 persons and only 4 persons got medals in all the three categories, how many received medals in exactly two of these categories?
A2)
Let A = set of persons who got medals in dance.
B = set of persons who got medals in dramatics.
C = set of persons who got medals in music.
Given,
n(A) = 36 n(B) = 12 n(C) = 18
n(A ∪ B ∪ C) = 45 n(A ∩ B ∩ C) = 4
We know that number of elements belonging to exactly two of the three sets A, B, C
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) - 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) - 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(A ∩ C) + n(A ∩ B ∩ C)
Therefore, n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) - n(A ∪ B ∪ C)
From (i) required number
= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) - n(A ∪ B ∪ C) - 12
= 36 + 12 + 18 + 4 - 45 - 12
= 70 - 57
= 13
Q3) Determine whether the following are functions
a) A = {(1, 2), (2, 3), (3, 4), (4, 5)}
b) B = {(1, 3), (0, 3), (2, 1), (4, 2)}
c) C = {(1, 6), (2, 5), (1, 9), (4, 3)}
A3)
a) A = {(1, 2), (2, 3), (3, 4), (4, 5)} is a function because all the first elements are different.
b) B = {(1, 3), (0, 3), (2, 1), (4, 2)} is a function because all the first elements are different. (The second element does not need to be unique)
c) C = {(1, 6), (2, 5), (1, 9), (4, 3)} is not a function because the first element, 1, is repeated.
Q4) Let A = {1, 2 ,4} and B = {1, 2, 2}
Find A X A & A X B
A4)
A X B = {1,1}{1,2}{1,2}, {2,1}{2,2}{2,2}, {4,1}{4,2}{4,2}, }
A X A = {1,1}{1,2}{1,2}, {2,1}{2,2}{2,2}, {4,1}{4,2}{4,2},
Q5) Consider the function f and g given by following relation.
f : {(1, -1), (2, -2), (3, -3), (4, - 4)}
g : {(-1, 1), (-2, 2), (-3, 3), (-4, 4)}
Show that g = f-1
A5)
(gof) (1) = g{f(1)}
= g (-1) = 1
(fog) (-1) = f {g(-1)}= f(1) = -1
And this is true for every y 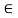 Y
Y
Hence g = f
Q6) Let A = { a, b, c, d, e } and let R and S be two Relation on A whose diagraph are shown:
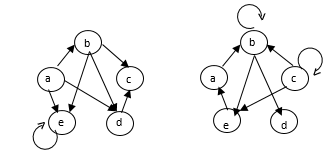
A6)

By diagraph.
R= { (a, b) (a,d) (a,e) (b,c) (b,d) (b,e) (c,c,) (d,d) (e,e)
S = { a, a) (a, b) (b,b) (b,e,) (c,c) (c,b) (c,e,) (d,b) (e,a,) (e,d)}
R= { elements of A XA which are not in R}
= { (a,a) (a,c), (b,a) (b,b) (c,a) (c,b) (c,d) (c,e,) (d,a) (d,b) (d,c) (d,e) (e,a) (e,b) (e,c) (e,d)}
R1 = {elements in R with reverse order }
= {(b,a,) (d,a) (e,a) (c,b) (d,b) (e,b) (c,c,) (d,d) (e,e)}
R⋂S = { elements common to both R & S}
{ (b,e, (c,c) }
R⋃S = { elements in R & S}
{ (a, a) (a,b) (a,d) (a,e) (b,b) (b,c) (b,d) (b,e) (c,c) (c,e,) (d,b)
(d,d) (e,a) (e,d) (e,e)}
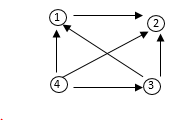
Q7) Let A = { 1, 2, 3, 4 } and let R be the relation greater than. Represent R as a set a diagraph, matrix and diagram.
A7)
R= { (2, 1), (3,1), (4,1), (3,2), (4,2) (4,3) }

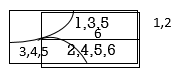
Q8) Let A = { 1, 2,3,4,5,6}. Find whether or not each of following is a portion of A
A8)
P = [{1,3,5}, {2, 4 ,5,6}]
 P= [{1,2}, {3,4,5}{6}]
P= [{1,2}, {3,4,5}{6}]