Unit – 4
Searching, Sorting and Hashing
Algorithm for Linear Search is
1. start at one end of the list
2. if the current element is not equal to the search target, move to the next element,
3. stop when a match is found or the opposite end of the list is reached.
Function for Linear search is
find(values, target)
{
for( i = 0; i < values.length; i++)
{
if (values[i] == target)
{ return i; }
}
return –1;
}
If element is found this function returns index of that element otherwise it returns –1.
Example : we have an array of integers, like the following:
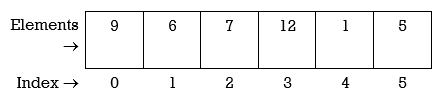
Let’s search for the number 7. According to function for linear search index for element 7 should be returned. We start at the beginning and check the first element in the array.
9 | 6 | 7 | 12 | 1 | 5 |
First element is 9.Match is not found and hence we move to next element i.e 6.
9 | 6 | 7 | 12 | 1 | 5 |
Again match is not found so move to next element i.e.7.
9 | 6 | 7 | 12 | 1 | 5 |
0 | 1 | 2 | 3 | 4 | 5 |
We found the match at the index position 2. Hence output is 2.
If we try to find element 10 in above array, it will return –1,as 10 is not present in the array.
2. Explain the complexity of linear search
Let us assume element x is to be searched in array A of size n.
An algorithm can be analyzed using following three cases.
1. Worst case
2. Average case
3. Best case
1. Worst case : In Linear search worst case happens when element to be searched is not present. When x is not present, the linear search function compares it with all the elements of A one by one. The size of A is n and hence x is to be compared with all n elements. Thus, the worst case time complexity of linear search would be O(n).
2. Average case : In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs. Following is the value of average case time complexity.
Average Case Time = =
= O (n)
3. Best Case : In linear search , the best case occurs when x is present at the first location. So time complexity in the best case would be O(1).
3. Write a program for linear search ?
#include<stdio.h>
#include<conio.h>
int search(int [],int, int);
void main()
{
int a[20],k,i,n,m;
clrscr();
printf(“\n\n ENTER THE SIZE OF ARRAY”);
scanf(“%d”,&n);
printf(“\n\nENTER THE ARRAY ELEMENTS\n\n”);
for(i=0;i<n;i++)
{
scanf(“%d”,&a[i]);
}
printf(“\n\nENTER THE ELEMENT FOR SEARCH\n”);
scanf(“%d”,&k);
m=search(a,n,k);
if(m==–1)
{
printf(“\n\nELEMENT IS NOT FOUND IN LIST”);
}
else
{
printf(“\n\nELEMENT IS FOUND AT LOCATION %d”,m);
}
}
getch();
}
int search(int a[],int n,int k)
{
int i;
for(i=0;i<n;i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return –1;
}
}
4. Write a program for binary search ?
#include<stdio.h>
#include<conio.h>
void main()
{
int n,i,search,f=0,low,high,mid,a[20];
clrscr();
printf("Enter the number of elements:");
scanf("%d",&n);
for(i=1;i<=n;i++)
{
printf("Enter the number in ascending order a[%d]=",i);
scanf("%d",&a[i]);
}
printf("Enter the element to be searched:");
scanf("%d",&search);
low=0;
high=n–1;
while(low<=high)
{
mid=(low+high)/2;
if(search<a[mid])
{
high=mid–1;
}
else if(search>a[mid])
{
low=mid+1;
}
else
{
f=1;
printf("Element is found at the position %d:",mid);
exit();
}
}
if(f==0)
{
printf("Element not found");
}
getch();
}
5. Explain selection sort algorithm?
Assume we want to sort list in ascending order. Selection sort finds the smallest element from unsorted list and swap it with the element in first position. Then it finds second smallest element and swap it with element at second position. This process is repeated till entire list is sorted in ascending order. Each time we swap elements, we say that we have completed a sort pass. A list of n elements requires n–1 passes to completely rearrange the data.
Procedure for every pass is as follows.
Pass 1 : Find the position P of the smallest in the list of N elements A[l], A[2], . . . , A[N], and then interchange A[P] and A[1] . Then A[1] is sorted.
Pass 2 : Find the position P of the smallest in the sublist of N –1 elements A[2], A[3],. . . , A[N], and then interchange A[P]and A[2]. Then A[l], A[2] is sorted.
Pass 3 : Find the position P of the smallest in the sublist of N–2 elements A[3], A[4], . . . , A[N], and then interchange A[P] and A[3]. Then: A[l], A[2] , A[3] is sorted.
Pass N –1 : Find the position P of the smaller of the elements A[N –1), A[N], and then interchange A[P] and A[N–1]. Then: A[l], A[2], . . . , A[N] is sorted. Thus A is sorted after N –1 passes.
Example 1 :
25 | 79 | 41 | 9 | 34 | 60 |
Fig. 4.2 : Original List
We will apply selection sort on this list.
Pass 1 :
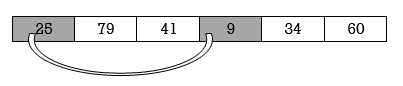
Here smallest element is 9 and 25 is located at first position. so we swap 9 with 25.
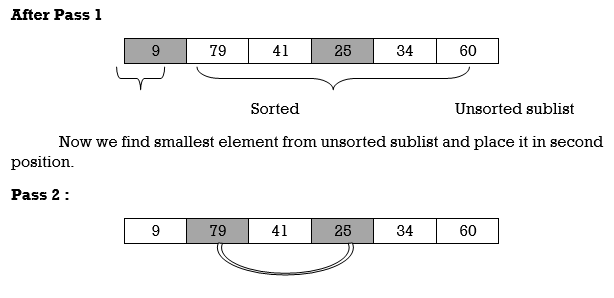 Unsorted sublist has 25 as a smallest element and 79 is located at second position. Hence we swap 25 and 79.
Unsorted sublist has 25 as a smallest element and 79 is located at second position. Hence we swap 25 and 79.
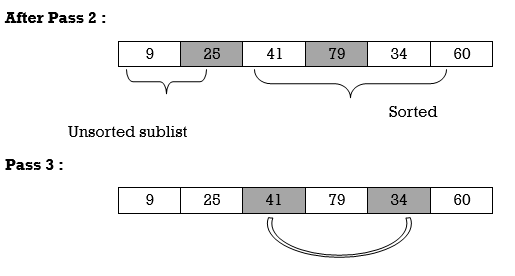
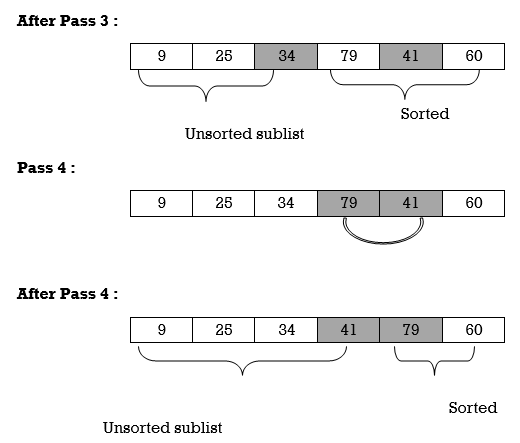
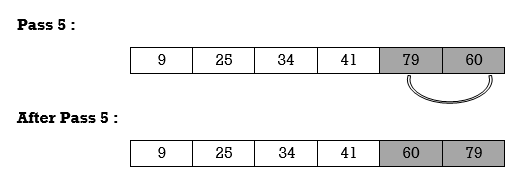
Thus list is sorted.
We will see one more example.
Apply selection sort on array A= {77,30,40,10,88,20,65,56}
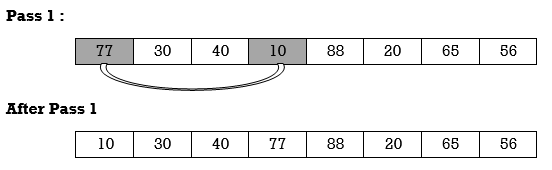
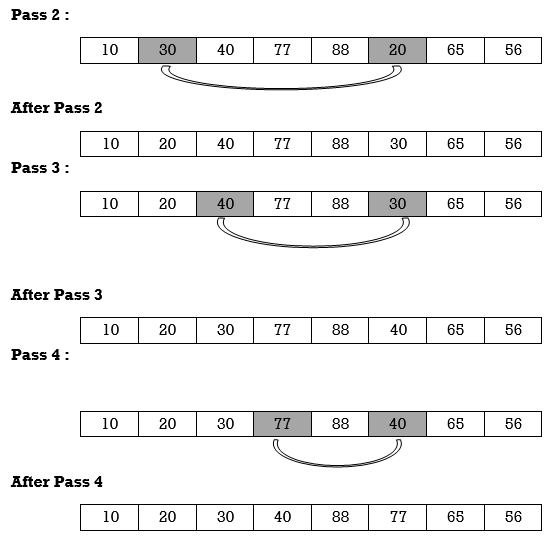
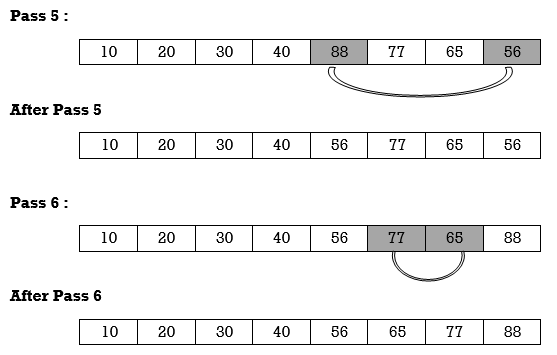 Hence the list is sorted in ascending order by applying selection sort.
Hence the list is sorted in ascending order by applying selection sort.
6. Write a program for bubble sort?
#include <stdio.h>
#include<conio.h>
void bubble_sort(int A[], int n);
int main()
{
int A[100], n, i, j, swap;
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter the elements\n", );
for (i = 0; i < n; i++)
scanf("%d", &A[i]);
bubble_sort(A, n);
printf("Sorted list in ascending order:\n");
for ( i = 0 ; i < n ; i++ )
printf("%ld\n", A[i]);
return 0;
}
void bubble_sort(int A[], int n)
{
int i, j, t;
for (i = 0 ; i < ( n – 1 ); i++)
{
for (j = 0 ; j < (n – i – 1); j++)
{
if (A[j] > list[j+1])
{
/* Swapping */
t = A[j];
A[j] = A[j+1];
A[j+1] = t;
}
}
}
}
7. Write a program for insertion sort?
#include <stdio.h>
int main()
{
int n, A[100], i, j, t;
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter %d integers\n", n);
for (i = 0; i < n; i++) {
scanf("%d", &A[i]);
}
for (i = 1 ; i <=( n – 1); i++)
{
j = i;
while ( j > 0 && A[j] < A[j–1])
{
t = A[j];
A[j] = A[j–1];
A[j–1] = t;
j––;
}
}
printf("Sorted list in ascending order:\n");
for (i = 0; i <= n – 1; i++) {
printf("%d\n", A[i]);
}
return 0;
}
8. Write a program for Quick sort algorithm?
#include<stdio.h>
void quicksort(int A[10],int,int);
int main(){
int A[20],n,i;
printf("Enter size of the array: ");
scanf("%d",&n);
printf("Enter %d elements: ",n);
for(i=0;i<n;i++)
scanf("%d",&A[i]);
quicksort(A,0,n–1);
printf("Sorted elements: ");
for(i=0;i<n;i++)
printf(" %d",A[i]);
return 0;
}
void quicksort(int A[20],int first, int last)
{
int pivot,j,temp,i;
if(first<last){
pivot=first;
i=first;
j=last;
while(i<j){
while(A[i]<=A[pivot]&&i<last)
i++;
while(A[j]>A[pivot])
j––;
if(i<j){
temp=A[i];
A[i]=A[j];
A[j]=temp;
}
}
temp=A[pivot];
A[pivot]=A[j];
A[j]=temp;
quicksort(A,first,j–1);
quicksort(A,j+1,last);
}
}
9. Explain merge sort?
Merge Sort is based on divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1 : Divide the list into sublists such that each sublist contains only one element.
Step 2 : Sort each sublist and Merge them.
Step 3 : Repeat Step 2 till the entire list is sorted.
Example : Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1 : A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
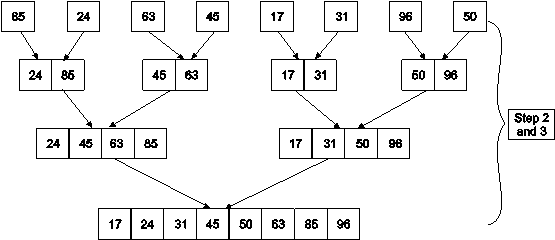
Fig.
Step 2 : Now we start from bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3 : Repeat this sorting and merging until entire list is sorted. Thus above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
10. Explain heap sort?
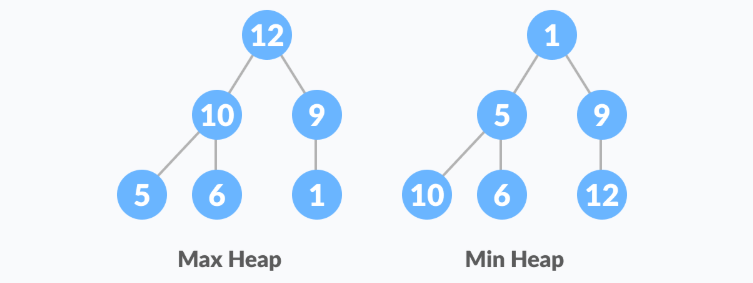
Heap is a special tree-based data structure. A binary tree is said to follow a heap data structure if it is a complete binary tree
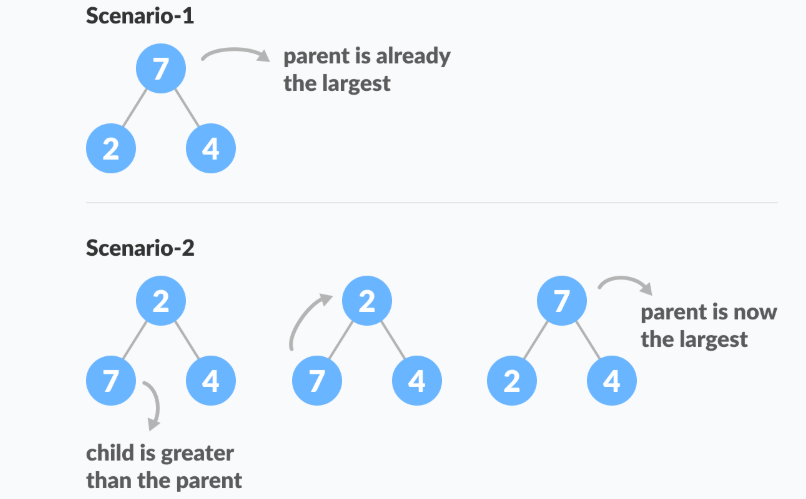
All nodes in the tree follow the property that they are greater than their children i.e. the largest element is at the root and both its children and smaller than the root and so on. Such a heap is called a max-heap. If instead, all nodes are smaller than their children, it is called a min-heap
The following example diagram shows Max-Heap and Min-Heap.
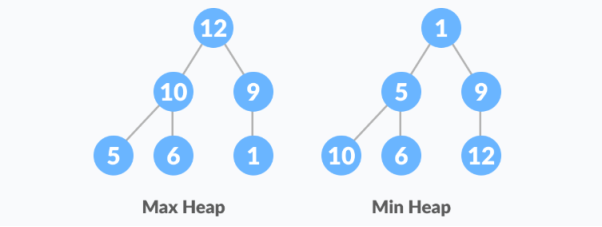
Starting from a complete binary tree, we can modify it to become a Max-Heap by running a function called heapify on all the non-leaf elements of the heap.
heapify(array)
Root = array[0]
Largest = largest( array[0] , array [2*0 + 1]. array[2*0+2])
if(Root != Largest)
Swap(Root, Largest)
The example above shows two scenarios - one in which the root is the largest element and we don't need to do anything. And another in which the root had a larger element as a child and we needed to swap to maintain max-heap property.
12.Explain hashing?
Hashing is an important Data Structure which is designed to use a special function called the Hash function which is used to map a given value with a particular key for faster access of elements. The efficiency of mapping depends of the efficiency of the hash function used.
Let a hash function H(x) maps the value  at the index x%10 in an Array. For example if the list of values is [11,12,13,14,15] it will be stored at positions {1,2,3,4,5} in the array or Hash table respectively.
at the index x%10 in an Array. For example if the list of values is [11,12,13,14,15] it will be stored at positions {1,2,3,4,5} in the array or Hash table respectively.