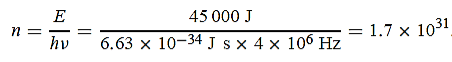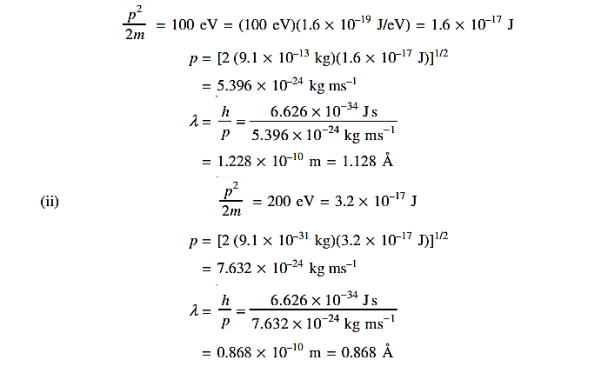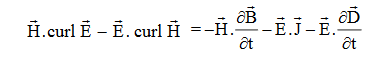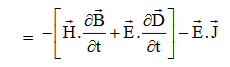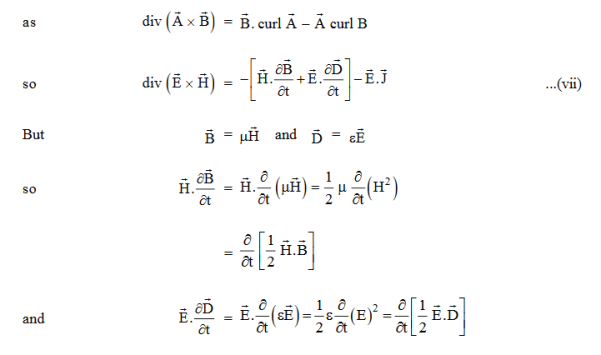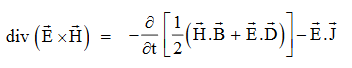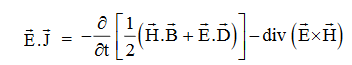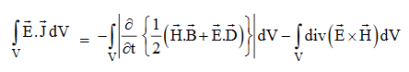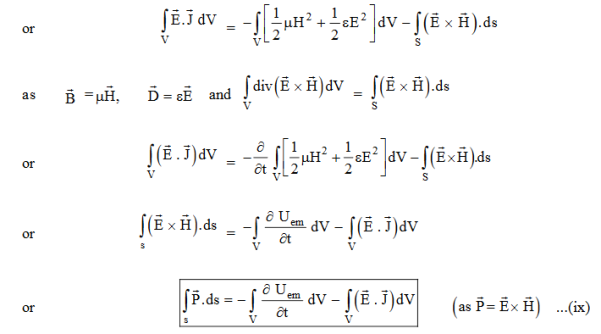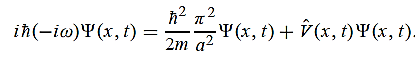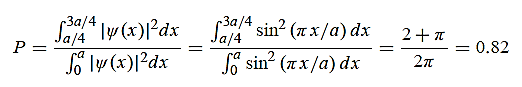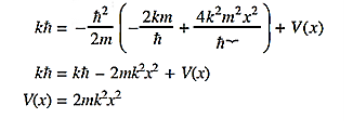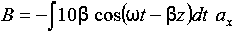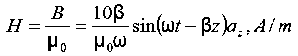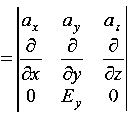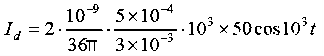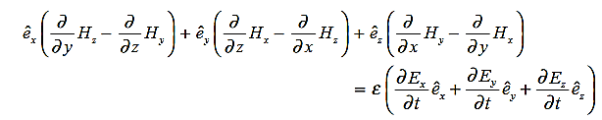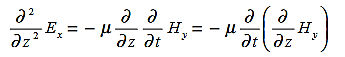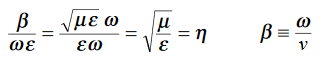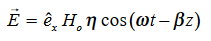PHY
UNIT – 3WAVE MECHANICS AND ELECTROMAGNETIC THEORYQ 1) Explain dual nature of matter?A 1)As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal. In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions. All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.So, starting from the momentum of a photon p = hν/c = h/λ. We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum  behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector 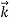 are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed. λ =
are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed. λ =  =
=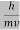 …….(1)
…….(1) 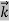 =
=  …….(2) Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore
…….(2) Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore =
= 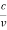 = λ Q 2) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?A 2) (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum
= λ Q 2) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?A 2) (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.Q 3) What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts?A 3)Accelerating potential V = 100 V. The de Broglie wavelength λ is λ= h /p = 1 227/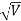 nmλ.1 227/
nmλ.1 227/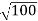 nm = 0.123 nmThe de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths.Q 4) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 4) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
nm = 0.123 nmThe de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths.Q 4) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 4) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
(b) Since the antenna emits a huge number of photons every second, 1.7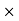 1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 5) Determine the de Broglie wavelength of an electron that has been accelerated through a potential difference of (i) 100 V, (ii) 200 V.A 5) (i)The energy gained by the electron = 100 eV. Then
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 5) Determine the de Broglie wavelength of an electron that has been accelerated through a potential difference of (i) 100 V, (ii) 200 V.A 5) (i)The energy gained by the electron = 100 eV. Then
Q 6) Calculate the de Broglie wavelength of an electron having a kinetic energy of 1000 eV. Compare the result with the wavelength of x-rays having the same energy?A 6)The kinetic energy
Q 7) List the conditions wave function should satisfy?A 7)The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x. The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity. However, this can represent the probability density of locating the particle at a place in a given instant of time. The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number. We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one. For the probability interpretation to make sense, the wave function must satisfy certain conditions. The wave function must be single valued at each point. The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1. ψ must be finite everywhere. ψ must be continuous everywhere and 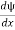 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite. ψ (x) must vanish ψ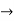 0 as x
0 as x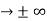 .
. The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere. so that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as 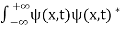 dx =1 Only wave function with all these properties can yield physically meaningful result. Q 8) What is Physical significance of wave function?A 8)
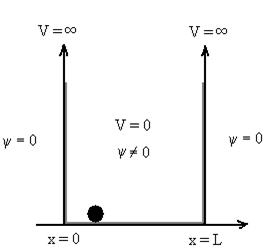
dx =1 Only wave function with all these properties can yield physically meaningful result. Q 8) What is Physical significance of wave function?A 8)The wave function ‘Ѱ’ has no physical meaning. it is a complex quantity representing the variation of a matter wave. The wave function Ѱ(r,t) describes the position of particle with respect to time . It can be considered as ‘probability amplitude’ since it is used to find the location of the particle. The square of the wave function gives the probability density of the particle which is represented by the wave function itself. More the value of probability density, more likely to find the particle in that region. Q 9) Discuss Particle in a One Dimensional Deep Potential WellA 9)Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.The potential function is expressed asV= 0 for 0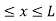 ………. (1)V=
………. (1)V= 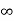 for x <0, x>L ………. (2)
for x <0, x>L ………. (2)
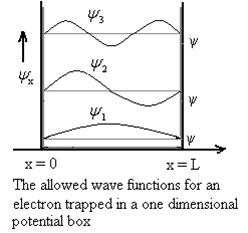
Figure : Particle in deep potential wellThe probability of finding the particle outside the well is zero (i.e. Ѱ =0) Inside the well, the Schrödinger wave equation is written as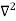 ψ +
ψ +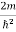 E ψ =0 …………….(2) Substituting
E ψ =0 …………….(2) Substituting 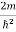 E = k2 …………….(3) writing the SWE for 1-D we get
E = k2 …………….(3) writing the SWE for 1-D we get 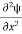 + k2 ψ =0 …………….(4) The general equation of above equation may be expressed asψ = Asin (kx + ϕ) …………….(5)Where A and ϕ are constants to be determined by boundary conditionsCondition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A
+ k2 ψ =0 …………….(4) The general equation of above equation may be expressed asψ = Asin (kx + ϕ) …………….(5)Where A and ϕ are constants to be determined by boundary conditionsCondition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A 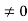 then sinϕ =0 or ϕ=0 …………….(6)Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)0 = Asin kL As A
then sinϕ =0 or ϕ=0 …………….(6)Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)0 = Asin kL As A 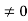 then sinkL =0 or kL=nπk =
then sinkL =0 or kL=nπk = 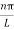 …………….(7)where n= 1,2,3,4………Substituting the value of k from (7) to (3)
…………….(7)where n= 1,2,3,4………Substituting the value of k from (7) to (3) 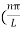 )2 =
)2 = 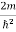 E This gives energy of level En =
E This gives energy of level En = 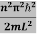 n=1,2,3,4…so on …………….(8)
n=1,2,3,4…so on …………….(8)
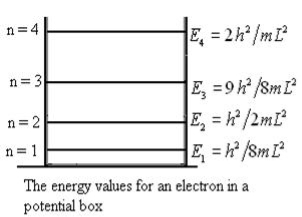
From equation En is the energy value (Eigen Value) of the particle in a well. It is clear that the energy values of the particle in well are discrete not continuous.
Using (6) and (7) equation (5) becomes, the corresponding wave functions will beψ = ψn = Asin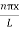 …………….(9)The probability density |ψ(x,t)|2 = ψ ψ*|ψ(x,t)|2 = A2sin2
…………….(9)The probability density |ψ(x,t)|2 = ψ ψ*|ψ(x,t)|2 = A2sin2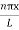 …………….(10)The probability density is zero at x = 0 and x = L. since the particle is always within the well
…………….(10)The probability density is zero at x = 0 and x = L. since the particle is always within the well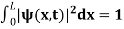 …………….(11)
…………….(11)
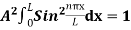
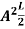 =1A =
=1A =  Substituting A in equation (9) we getψ = ψn =
Substituting A in equation (9) we getψ = ψn = 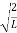 sin
sin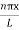 n=1,2,3,4….. …………….(12)The above equation (12) is normalized wave function or Eigen function belonging to energy value En
n=1,2,3,4….. …………….(12)The above equation (12) is normalized wave function or Eigen function belonging to energy value En
Figure: Wave function for ParticleTherefore, according to uncertainty principle it is difficult to assign a position to the electron
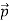 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector 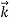 are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed. λ =
are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed. λ =  =
=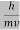 …….(1)
…….(1) 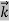 =
=  …….(2) Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore
…….(2) Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore =
= 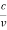 = λ Q 2) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?A 2) (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum
= λ Q 2) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?A 2) (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s) p = 4.92 × 10–24 kg m/s de Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s λ= 0.135 nm (b)For the ball: Mass m’ = 0.150 kg, Speed v ’= 30.0 m/s. Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s) p’= 4.50 kg m/s de Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m |
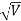 nmλ.1 227/
nmλ.1 227/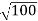 nm = 0.123 nmThe de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths.Q 4) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 4) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
nm = 0.123 nmThe de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths.Q 4) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 4) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
|
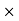 1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 5) Determine the de Broglie wavelength of an electron that has been accelerated through a potential difference of (i) 100 V, (ii) 200 V.A 5) (i)The energy gained by the electron = 100 eV. Then
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 5) Determine the de Broglie wavelength of an electron that has been accelerated through a potential difference of (i) 100 V, (ii) 200 V.A 5) (i)The energy gained by the electron = 100 eV. Then
|
|
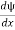 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite.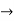 0 as x
0 as x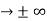 .
.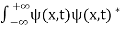 dx =1 Only wave function with all these properties can yield physically meaningful result. Q 8) What is Physical significance of wave function?A 8)
dx =1 Only wave function with all these properties can yield physically meaningful result. Q 8) What is Physical significance of wave function?A 8)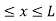 ………. (1)V=
………. (1)V= 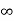 for x <0, x>L ………. (2)
for x <0, x>L ………. (2)
|
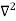 ψ +
ψ +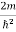 E ψ =0 …………….(2) Substituting
E ψ =0 …………….(2) Substituting 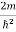 E = k2 …………….(3) writing the SWE for 1-D we get
E = k2 …………….(3) writing the SWE for 1-D we get 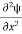 + k2 ψ =0 …………….(4) The general equation of above equation may be expressed asψ = Asin (kx + ϕ) …………….(5)Where A and ϕ are constants to be determined by boundary conditionsCondition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A
+ k2 ψ =0 …………….(4) The general equation of above equation may be expressed asψ = Asin (kx + ϕ) …………….(5)Where A and ϕ are constants to be determined by boundary conditionsCondition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A 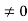 then sinϕ =0 or ϕ=0 …………….(6)Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)0 = Asin kL As A
then sinϕ =0 or ϕ=0 …………….(6)Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)0 = Asin kL As A 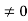 then sinkL =0 or kL=nπk =
then sinkL =0 or kL=nπk = 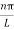 …………….(7)where n= 1,2,3,4………Substituting the value of k from (7) to (3)
…………….(7)where n= 1,2,3,4………Substituting the value of k from (7) to (3) 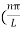 )2 =
)2 = 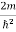 E This gives energy of level En =
E This gives energy of level En = 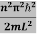 n=1,2,3,4…so on …………….(8)
n=1,2,3,4…so on …………….(8) From equation En is the energy value (Eigen Value) of the particle in a well. It is clear that the energy values of the particle in well are discrete not continuous.
|
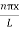 …………….(9)The probability density |ψ(x,t)|2 = ψ ψ*|ψ(x,t)|2 = A2sin2
…………….(9)The probability density |ψ(x,t)|2 = ψ ψ*|ψ(x,t)|2 = A2sin2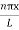 …………….(10)The probability density is zero at x = 0 and x = L. since the particle is always within the well
…………….(10)The probability density is zero at x = 0 and x = L. since the particle is always within the well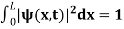 …………….(11)
…………….(11)
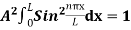
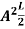 =1A =
=1A =  Substituting A in equation (9) we getψ = ψn =
Substituting A in equation (9) we getψ = ψn = 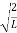 sin
sin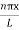 n=1,2,3,4….. …………….(12)The above equation (12) is normalized wave function or Eigen function belonging to energy value En
n=1,2,3,4….. …………….(12)The above equation (12) is normalized wave function or Eigen function belonging to energy value En
|
.Q 10) Discuss Poynting Theorem?A 10)When electromagnetic wave travels in space, it carries energy and energy density is always associated with electric fields and magnetic fields.The rate of energy travelled through per unit area i.e. the amount of energy flowing through per unit area in the perpendicular direction to the incident energy per unit time is called Poynting vector.Mathematically Poynting vector is represented as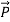 =
= 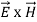 =(
=( 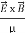 ) (i)The direction of Poynting vector is perpendicular to the plane containing
) (i)The direction of Poynting vector is perpendicular to the plane containing 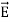 and
and 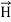 . Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer
. Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer 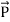 is perpendicular to both
is perpendicular to both 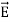 and
and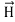 . It represents the rate of energy transfer per unit area.UNITIts unit is W/m2.Poynting TheoremPoynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses.i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of chargeProof The energy density carried by the electromagnetic wave can be calculated using Maxwell's equationsdiv
. It represents the rate of energy transfer per unit area.UNITIts unit is W/m2.Poynting TheoremPoynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses.i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of chargeProof The energy density carried by the electromagnetic wave can be calculated using Maxwell's equationsdiv  = 0 ...(i) div
= 0 ...(i) div  =0 ...(ii) Curl
=0 ...(ii) Curl 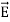 = -
= - 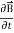 …(iii)Curl
…(iii)Curl 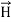 =
=  +
+ 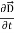 …(iv)Taking scalar product of (3) with H and (4) with
…(iv)Taking scalar product of (3) with H and (4) with 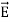 i.e.
i.e.  curl
curl 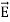 = -
= - 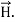
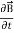 ……(v)and
……(v)and 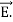 curl
curl 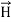 =
= 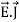 +
+ 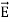 .
. 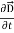 …..(vi)Doing (vi) – (v) i.e.
…..(vi)Doing (vi) – (v) i.e.
So from equation (vii)
Or
Integrating equation (viii) over a volume V enclosed by a Surface S
Total power leaving the volume = rate of decrease of stored e.m. energy -ohmic power dissipated due to charge motionThis equation (ix) represents the Poynting theorem according to which the net power flowing out of a given volume is equal to the rate of decrease of stored electromagnetic energy in that volume minus the conduction losses. In equation (ix) 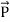 .ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.The term represent
.ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.The term represent
the energy stored in electric and magnetic fields respectively and their sum denotes the total energy stored in electromagnetic field. So total terms gives the rate of decrease of energy stored in volume V due to electric and magnetic fields.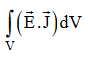 Gives the rate of energy transferred into the electromagnetic field.This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism.Q 11) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 11) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
Gives the rate of energy transferred into the electromagnetic field.This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism.Q 11) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 11) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
(b) Since the antenna emits a huge number of photons every second, 1.7 1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 12) Consider a one-dimensional particle which is confined within the region 0
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 12) Consider a one-dimensional particle which is confined within the region 0  x
x a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4
a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4  x
x  3a/4.A 12)Since the first time derivative and the second x derivative of (x, t), are given by
3a/4.A 12)Since the first time derivative and the second x derivative of (x, t), are given by 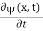 =-iω (x, t) and
=-iω (x, t) and 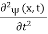 =- (π2/a2) (x, t) the Schrödinger equation yields
=- (π2/a2) (x, t) the Schrödinger equation yields
Hence V(x,t) is time independent and given by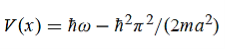 (b) The probability of finding the particle in the interval a/4
(b) The probability of finding the particle in the interval a/4  x
x 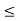 3a/4.can be obtained from
3a/4.can be obtained from
Q 13) The wave function of a particle of mass m moving in a potential V (x) is 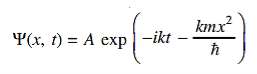 where A and k are constants. Find the explicit form of the potential V (x).A 13)
where A and k are constants. Find the explicit form of the potential V (x).A 13)
Substituting these values in the time dependendent Schrödinger equation, we have
Q 14) Given E = 10 sin (t-y) ay V/m, in free space, determine D, B and H.A 14)E = 10 sin (t-y) ay, V/mD =0E,0= 8.854 x 10-12 F/mD = 100sin (t-y) ay, C/m2Second Maxwell’s equation isx E = -BThat is,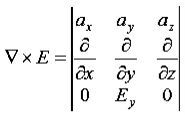 or
or
As Ey= 10 sin (t-z) V/m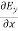 = 0Now,x E becomesx E = -
= 0Now,x E becomesx E = -  ax= 10 cos (t-z) ax= -
ax= 10 cos (t-z) ax= - 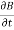
Q 15) If the electric field strength, E of an electromagnetic wave in free space is given by E = 2 cos (t - 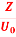 ) ay V/m,Find the magnetic field, HA 15)We have B/t =-x E
) ay V/m,Find the magnetic field, HA 15)We have B/t =-x E
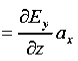
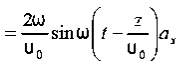
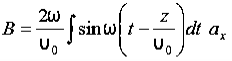
 Thus
Thus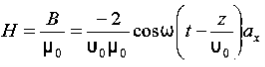 Also
Also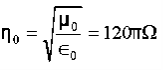
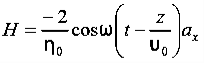
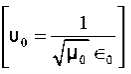
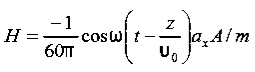 Q 16) A parallel-plate capacitor with plate area of 5 cm2and plate separations of 3 mm has a voltage 50 sin 103t V applied to its plates. Calculate the displacement current assuming = 20.A 16)D =EJd =
Q 16) A parallel-plate capacitor with plate area of 5 cm2and plate separations of 3 mm has a voltage 50 sin 103t V applied to its plates. Calculate the displacement current assuming = 20.A 16)D =EJd =  =
=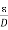
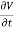 Hence,Id = Jd. S =
Hence,Id = Jd. S = 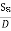
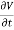 =
= 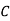
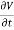 which is the same as the conduction current, given by
which is the same as the conduction current, given by
= 147.4 cos 103t nAQ 17) Write a note on displacement current?A 17)Displacement current is the rate of change of electric displacement field.The type of current which passes through a conductor is known as conduction current and is caused by the actual movement of electrons through the conductor. This type of current is mostly used in our day to day life. There is also another kind of current, which is known as displacement current. Displacement current differs from the conduction current because the displacement current does not involve electrons' movement. The displacement current has enormous importance for the propagation of electromagnetic waves. In electromagnetism, displacement current is a quantity appearing in Maxwell's equations that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do.It is mathematically represented as ID = JD S = S 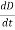 Where S = Area of the plate of the capacitor ID = Displacement currentJD = Displacement current densityD = εE where ε is permittivity of the medium During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor. Q 18) Give Physical Significance of Maxwell’s equation?A 18)Physical significance of Maxwell’s Ist equation∇·E = ρ/ε0According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.Physical significance of Maxwell’s 2nd equation ∇·B = 0It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.Physical significance of Maxwell’s 3rd equation ∇×E = −∂B/∂t It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.Physical significance of Maxwell’s 4th equation∇×H = J + ∂D/∂t This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.Q 19) Write down solution for plane electromagnetic waves in vacuum?A 19)In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.Solutions of Maxwell’s Equations - Uniform Plane WavesThe sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.
Where S = Area of the plate of the capacitor ID = Displacement currentJD = Displacement current densityD = εE where ε is permittivity of the medium During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor. Q 18) Give Physical Significance of Maxwell’s equation?A 18)Physical significance of Maxwell’s Ist equation∇·E = ρ/ε0According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.Physical significance of Maxwell’s 2nd equation ∇·B = 0It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.Physical significance of Maxwell’s 3rd equation ∇×E = −∂B/∂t It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.Physical significance of Maxwell’s 4th equation∇×H = J + ∂D/∂t This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.Q 19) Write down solution for plane electromagnetic waves in vacuum?A 19)In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.Solutions of Maxwell’s Equations - Uniform Plane WavesThe sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.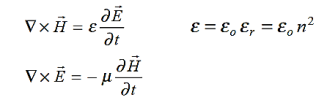 These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:(i) Find what kind of source would generate this type of field (waves).(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.Assumption for Solution: Can we find a solution such that:1.) No variation exists in x and y directions.2.)
These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:(i) Find what kind of source would generate this type of field (waves).(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.Assumption for Solution: Can we find a solution such that:1.) No variation exists in x and y directions.2.) 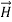 or
or 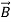 also is oriented along one of the axes.Ampere’s Law becomes:
also is oriented along one of the axes.Ampere’s Law becomes:
or, with our assumptions: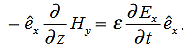 Compare for transmission line:
Compare for transmission line: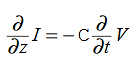 In a similar manner,
In a similar manner, 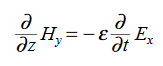 ………….(1)Faraday’s Law becomes:
………….(1)Faraday’s Law becomes: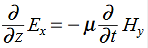 ………….(2)Thus, if
………….(2)Thus, if 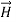 is only in the
is only in the 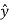 direction, then is only in the .If we differentiate (2) with respect to z, we get:
direction, then is only in the .If we differentiate (2) with respect to z, we get:
Substitute from (2),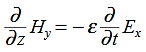 We get
We get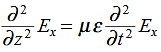 This is called the wave equation.Compare for transmission line: (same).
This is called the wave equation.Compare for transmission line: (same).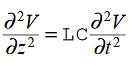 We will assume dielectric media; lossless:
We will assume dielectric media; lossless: 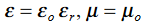 Dimensional analysis:
Dimensional analysis: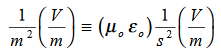
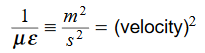 In the units we are using:
In the units we are using: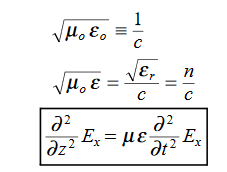 By exactly the same method, we also get:
By exactly the same method, we also get: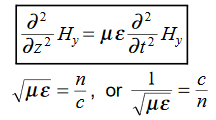 For example, the same equation is true for
For example, the same equation is true for 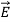 and
and 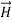 . Thus,
. Thus, 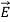 and
and 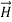 must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that
must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that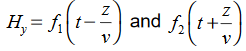 are the solutions
are the solutions t is important to note that f1 and f2 can be any function.The field we find directly from the equation:
t is important to note that f1 and f2 can be any function.The field we find directly from the equation: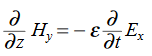 Suppose
Suppose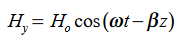 …………(3)Differentiate (3) with respect to z
…………(3)Differentiate (3) with respect to z 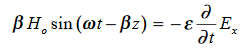 …………(4)Integrate with respect to time
…………(4)Integrate with respect to time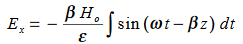 …………(5)
…………(5)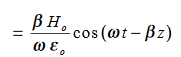 This leads to a new quantity that relates the electric and magnetic fields:
This leads to a new quantity that relates the electric and magnetic fields:
Rewriting:Units of  =
=  =
= 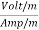 = Ω
= Ω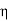 0 = Impedance of free space =
0 = Impedance of free space = 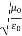 =377 Ω
=377 Ω = impedance of a lossless dielectric =
= impedance of a lossless dielectric =  =
=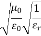 =
= 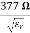 Note that
Note that  and
and 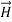 are in time phase and space quadratureThe directions of the vectors are such that:
are in time phase and space quadratureThe directions of the vectors are such that:
This vector 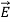
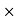
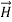 , always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves. “Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant). “Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves.Q 20) Discuss Maxwell’s equations ?A 20)Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects. Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization. We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed. Maxwell’s first equation (Gauss' Law for Electric Fields)Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as: ∇·E = ρ/ε0 0r∇·D = ρ Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).Maxwell’s second equation (Faraday's Law)Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.∇×E = −∂B/∂t (2)Maxwell’s third equation (Ampere's Law)Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced. This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon. The modified form of Ampere's Law s given by Maxwell’s third equation∇×H = J + ∂D/∂t Maxwell’s four equation (Gauss' Magnetism law)we know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero. Why? Why isn't the divergence of B equal to the magnetic charge density? Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero: ∇·B = 0 Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.Maxwell’s four equations are given by∇·E = ρ/ε0 (1)∇×E = −∂B/∂t (2)∇×H = J + ∂D/∂t (3)∇·B = 0 (4)These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,∇=(∂/∂x, ∂/∂y, ∂/∂z)E is the electric vectorB is the magnetic inductionρ is the electric charge density j is the electric current densityε0 is the permittivity of free spacec is the speed of light. In addition to Maxwell equations, the following identities are useful: J = σE (5)D = εE (6)B = μH (7) Here, D is the electric displacement H is the magnetic vector σ is the specific conductivityε is the dielectric constant (or permittivity) μ is the magnetic permeability
, always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves. “Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant). “Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves.Q 20) Discuss Maxwell’s equations ?A 20)Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects. Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization. We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed. Maxwell’s first equation (Gauss' Law for Electric Fields)Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as: ∇·E = ρ/ε0 0r∇·D = ρ Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).Maxwell’s second equation (Faraday's Law)Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.∇×E = −∂B/∂t (2)Maxwell’s third equation (Ampere's Law)Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced. This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon. The modified form of Ampere's Law s given by Maxwell’s third equation∇×H = J + ∂D/∂t Maxwell’s four equation (Gauss' Magnetism law)we know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero. Why? Why isn't the divergence of B equal to the magnetic charge density? Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero: ∇·B = 0 Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.Maxwell’s four equations are given by∇·E = ρ/ε0 (1)∇×E = −∂B/∂t (2)∇×H = J + ∂D/∂t (3)∇·B = 0 (4)These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,∇=(∂/∂x, ∂/∂y, ∂/∂z)E is the electric vectorB is the magnetic inductionρ is the electric charge density j is the electric current densityε0 is the permittivity of free spacec is the speed of light. In addition to Maxwell equations, the following identities are useful: J = σE (5)D = εE (6)B = μH (7) Here, D is the electric displacement H is the magnetic vector σ is the specific conductivityε is the dielectric constant (or permittivity) μ is the magnetic permeability
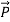 =
= 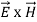 =(
=( 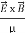 ) (i)The direction of Poynting vector is perpendicular to the plane containing
) (i)The direction of Poynting vector is perpendicular to the plane containing 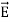 and
and 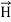 . Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer
. Poynting vector is also called as instantaneous energy flux density. Here rate of energy transfer 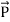 is perpendicular to both
is perpendicular to both 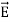 and
and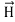 . It represents the rate of energy transfer per unit area.UNITIts unit is W/m2.Poynting TheoremPoynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses.i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of chargeProof The energy density carried by the electromagnetic wave can be calculated using Maxwell's equationsdiv
. It represents the rate of energy transfer per unit area.UNITIts unit is W/m2.Poynting TheoremPoynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses.i.e. total power leaving the volume =Rate of decrease of stored electromagnetic energy – ohmic power dissipated due to motion of chargeProof The energy density carried by the electromagnetic wave can be calculated using Maxwell's equationsdiv  = 0 ...(i) div
= 0 ...(i) div  =0 ...(ii) Curl
=0 ...(ii) Curl 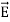 = -
= - 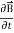 …(iii)Curl
…(iii)Curl 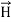 =
=  +
+ 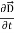 …(iv)Taking scalar product of (3) with H and (4) with
…(iv)Taking scalar product of (3) with H and (4) with 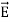 i.e.
i.e.  curl
curl 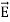 = -
= - 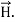
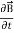 ……(v)and
……(v)and 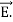 curl
curl 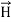 =
= 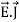 +
+ 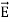 .
. 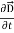 …..(vi)Doing (vi) – (v) i.e.
…..(vi)Doing (vi) – (v) i.e.
|
|
|
|
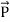 .ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.The term represent
.ds represents the amount of electromagnetic energy crossing the closed surface per second or the rate of flow of outward energy through the surface S enclosing volume V i.e. it is Poynting vector.The term represent
|
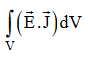 Gives the rate of energy transferred into the electromagnetic field.This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism.Q 11) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 11) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
Gives the rate of energy transferred into the electromagnetic field.This is also known as work-energy theorem. This is also called as the energy conservation law in electromagnetism.Q 11) A 45 kW broadcasting antenna emits radio waves at a frequency of 4 MHz.(a) How many photons are emitted per second?(b) Is the quantum nature of the electromagnetic radiation important in analyzing the radiation emitted from this antenna?A 11) (a) The electromagnetic energy emitted by the antenna in one second is E = 45 000 J. Thus, the number of photons emitted in one second is
|
 1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 12) Consider a one-dimensional particle which is confined within the region 0
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q 12) Consider a one-dimensional particle which is confined within the region 0  x
x a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4
a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4  x
x  3a/4.A 12)Since the first time derivative and the second x derivative of (x, t), are given by
3a/4.A 12)Since the first time derivative and the second x derivative of (x, t), are given by 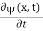 =-iω (x, t) and
=-iω (x, t) and 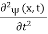 =- (π2/a2) (x, t) the Schrödinger equation yields
=- (π2/a2) (x, t) the Schrödinger equation yields
|
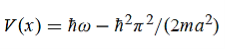 (b) The probability of finding the particle in the interval a/4
(b) The probability of finding the particle in the interval a/4  x
x 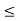 3a/4.can be obtained from
3a/4.can be obtained from
|
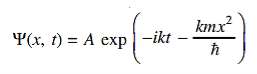 where A and k are constants. Find the explicit form of the potential V (x).A 13)
where A and k are constants. Find the explicit form of the potential V (x).A 13)
|
|
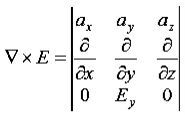 or
or
|
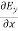 = 0Now,x E becomesx E = -
= 0Now,x E becomesx E = -  ax= 10 cos (t-z) ax= -
ax= 10 cos (t-z) ax= - 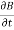
|
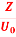 ) ay V/m,Find the magnetic field, HA 15)We have B/t =-x E
) ay V/m,Find the magnetic field, HA 15)We have B/t =-x E
|
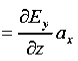
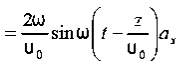
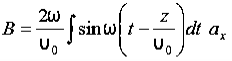
 Thus
Thus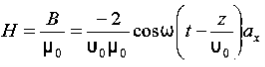 Also
Also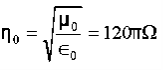
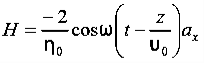
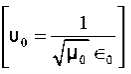
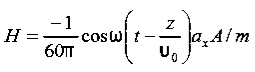 Q 16) A parallel-plate capacitor with plate area of 5 cm2and plate separations of 3 mm has a voltage 50 sin 103t V applied to its plates. Calculate the displacement current assuming = 20.A 16)D =EJd =
Q 16) A parallel-plate capacitor with plate area of 5 cm2and plate separations of 3 mm has a voltage 50 sin 103t V applied to its plates. Calculate the displacement current assuming = 20.A 16)D =EJd =  =
=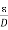
 Hence,Id = Jd. S =
Hence,Id = Jd. S = 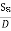
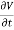 =
= 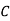
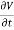 which is the same as the conduction current, given by
which is the same as the conduction current, given by
|
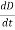 Where S = Area of the plate of the capacitor ID = Displacement currentJD = Displacement current densityD = εE where ε is permittivity of the medium During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor. Q 18) Give Physical Significance of Maxwell’s equation?A 18)Physical significance of Maxwell’s Ist equation∇·E = ρ/ε0According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.Physical significance of Maxwell’s 2nd equation ∇·B = 0It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.Physical significance of Maxwell’s 3rd equation ∇×E = −∂B/∂t It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.Physical significance of Maxwell’s 4th equation∇×H = J + ∂D/∂t This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.Q 19) Write down solution for plane electromagnetic waves in vacuum?A 19)In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.Solutions of Maxwell’s Equations - Uniform Plane WavesThe sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.
Where S = Area of the plate of the capacitor ID = Displacement currentJD = Displacement current densityD = εE where ε is permittivity of the medium During the charging and discharging process of the capacitor, the electric current flows through the wires of the circuit. However, no current flow between the plates of the capacitor. Q 18) Give Physical Significance of Maxwell’s equation?A 18)Physical significance of Maxwell’s Ist equation∇·E = ρ/ε0According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.Physical significance of Maxwell’s 2nd equation ∇·B = 0It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.Physical significance of Maxwell’s 3rd equation ∇×E = −∂B/∂t It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.Physical significance of Maxwell’s 4th equation∇×H = J + ∂D/∂t This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.Q 19) Write down solution for plane electromagnetic waves in vacuum?A 19)In an electromagnetic wave, electric and magnetic field vectors are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave. This nature of electromagnetic wave is known as Transverse nature.Maxwell proved that both the electric and magnetic fields are perpendicular to each other in the direction of wave propagation. He considered an electromagnetic wave propagating along positive x-axis. When a rectangular parallelepiped was placed parallel to the three co-ordinate axis, the electric and magnetic fields propagate sinusoidal with the x-axis and are independent of y and z-axis.A wave in which the values of variable are constant in a plane perpendicular to the direction of propagation of the wave is called plane wave. These planes may also termed as wave fronts.Solutions of Maxwell’s Equations - Uniform Plane WavesThe sources of time varying electromagnetic fields are time varying charges and currents, whether man-made or naturally occurring. However, examination of Maxwell’s equations shows that, even in empty space (with no sources), and fields cause each other. This means that, although these fields must originate in source regions, they can propagate through source-free regions. Because solutions in source regions are very hard to obtain, let us consider what kind of fields can exist in source-free regions.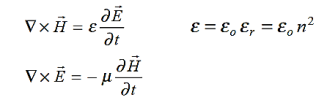 These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:(i) Find what kind of source would generate this type of field (waves).(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.Assumption for Solution: Can we find a solution such that:1.) No variation exists in x and y directions.2.)
These equations are still very complicated (4 different partial derivatives). Let’s try to find simple solutions. We do this by making assumptions. After finding simplest solutions, we:(i) Find what kind of source would generate this type of field (waves).(ii) Show that these simple solutions are useful approximations to real electromagnetic waves.Assumption for Solution: Can we find a solution such that:1.) No variation exists in x and y directions.2.) 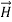 or
or 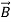 also is oriented along one of the axes.Ampere’s Law becomes:
also is oriented along one of the axes.Ampere’s Law becomes:
|
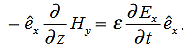 Compare for transmission line:
Compare for transmission line: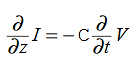 In a similar manner,
In a similar manner, 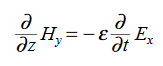 ………….(1)Faraday’s Law becomes:
………….(1)Faraday’s Law becomes: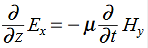 ………….(2)Thus, if
………….(2)Thus, if 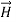 is only in the
is only in the 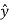 direction, then is only in the .If we differentiate (2) with respect to z, we get:
direction, then is only in the .If we differentiate (2) with respect to z, we get:
|
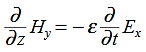 We get
We get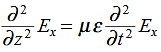 This is called the wave equation.Compare for transmission line: (same).
This is called the wave equation.Compare for transmission line: (same).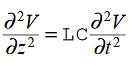 We will assume dielectric media; lossless:
We will assume dielectric media; lossless: 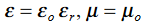 Dimensional analysis:
Dimensional analysis: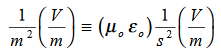
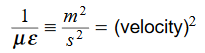 In the units we are using:
In the units we are using: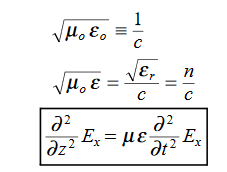 By exactly the same method, we also get:
By exactly the same method, we also get: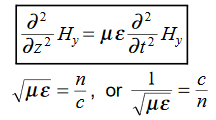 For example, the same equation is true for
For example, the same equation is true for  and
and  . Thus,
. Thus, 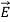 and
and 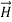 must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that
must have the same type of functional dependence. This wave equation still has many possible solutions. In fact, it can be shown by direct substitution that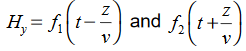 are the solutions
are the solutions t is important to note that f1 and f2 can be any function.The field we find directly from the equation:
t is important to note that f1 and f2 can be any function.The field we find directly from the equation: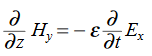 Suppose
Suppose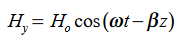 …………(3)Differentiate (3) with respect to z
…………(3)Differentiate (3) with respect to z 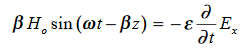 …………(4)Integrate with respect to time
…………(4)Integrate with respect to time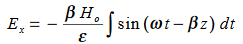 …………(5)
…………(5)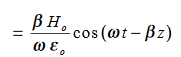 This leads to a new quantity that relates the electric and magnetic fields:
This leads to a new quantity that relates the electric and magnetic fields:
|
 =
=  =
= 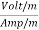 = Ω
= Ω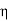 0 = Impedance of free space =
0 = Impedance of free space = 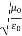 =377 Ω
=377 Ω = impedance of a lossless dielectric =
= impedance of a lossless dielectric =  =
=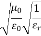 =
= 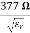 Note that
Note that  and
and 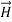 are in time phase and space quadratureThe directions of the vectors are such that:
are in time phase and space quadratureThe directions of the vectors are such that:
|
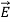
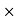
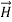 , always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves. “Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant). “Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves.Q 20) Discuss Maxwell’s equations ?A 20)Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects. Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization. We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed. Maxwell’s first equation (Gauss' Law for Electric Fields)Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as: ∇·E = ρ/ε0 0r∇·D = ρ Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).Maxwell’s second equation (Faraday's Law)Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.∇×E = −∂B/∂t (2)Maxwell’s third equation (Ampere's Law)Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced. This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon. The modified form of Ampere's Law s given by Maxwell’s third equation∇×H = J + ∂D/∂t Maxwell’s four equation (Gauss' Magnetism law)we know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero. Why? Why isn't the divergence of B equal to the magnetic charge density? Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero: ∇·B = 0 Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.Maxwell’s four equations are given by∇·E = ρ/ε0 (1)∇×E = −∂B/∂t (2)∇×H = J + ∂D/∂t (3)∇·B = 0 (4)These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,∇=(∂/∂x, ∂/∂y, ∂/∂z)E is the electric vectorB is the magnetic inductionρ is the electric charge density j is the electric current densityε0 is the permittivity of free spacec is the speed of light. In addition to Maxwell equations, the following identities are useful: J = σE (5)D = εE (6)B = μH (7) Here, D is the electric displacement H is the magnetic vector σ is the specific conductivityε is the dielectric constant (or permittivity) μ is the magnetic permeability
, always points in the direction of propagation. These types of waves are called Uniform Plane Electromagnetic Waves. “Plane” refers to the fact that, at any instant in time, the surfaces of constant phase are planes (here, constant). “Uniform” means no variation in transverse direction. The wave derived here is one oscillating at a single frequency. The frequency is determined by the source. If the source has multiple frequencies, so will the wave. In communications, modulating a carrier wave results in multiple frequencies. But before we can study such fields, we must thoroughly understand single frequency sinusoidal waves.Q 20) Discuss Maxwell’s equations ?A 20)Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects. Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization. We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed. Maxwell’s first equation (Gauss' Law for Electric Fields)Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as: ∇·E = ρ/ε0 0r∇·D = ρ Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).Maxwell’s second equation (Faraday's Law)Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.∇×E = −∂B/∂t (2)Maxwell’s third equation (Ampere's Law)Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced. This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon. The modified form of Ampere's Law s given by Maxwell’s third equation∇×H = J + ∂D/∂t Maxwell’s four equation (Gauss' Magnetism law)we know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero. Why? Why isn't the divergence of B equal to the magnetic charge density? Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero: ∇·B = 0 Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.Maxwell’s four equations are given by∇·E = ρ/ε0 (1)∇×E = −∂B/∂t (2)∇×H = J + ∂D/∂t (3)∇·B = 0 (4)These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,∇=(∂/∂x, ∂/∂y, ∂/∂z)E is the electric vectorB is the magnetic inductionρ is the electric charge density j is the electric current densityε0 is the permittivity of free spacec is the speed of light. In addition to Maxwell equations, the following identities are useful: J = σE (5)D = εE (6)B = μH (7) Here, D is the electric displacement H is the magnetic vector σ is the specific conductivityε is the dielectric constant (or permittivity) μ is the magnetic permeability0 matching results found