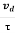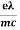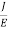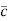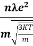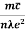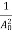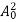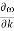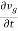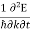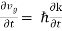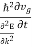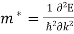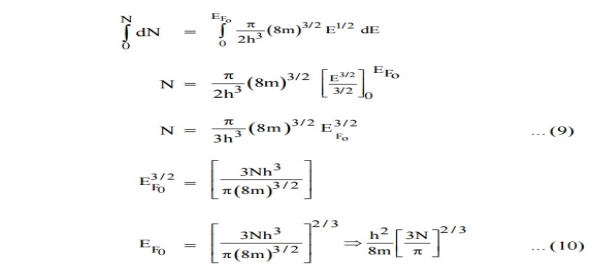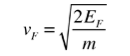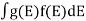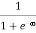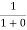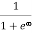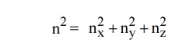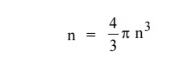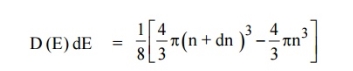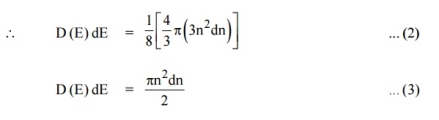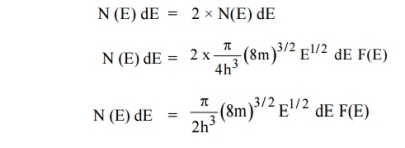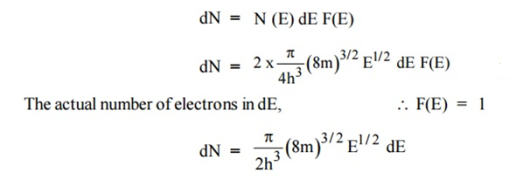kT. It is related to the kinetic energy equation
kT. It is related to the kinetic energy equation
|
F = eE ........(1) |
Force F = ma …....(2) |
ma = eE or a = Acceleration (a) = Or a = |
So vd = a ……….(4) |
vd = vd = |
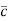 = RMS velocityThe Ohms’ law states that current density (J) is expressed as
= RMS velocityThe Ohms’ law states that current density (J) is expressed as J =E ……….(6) Or = |
J = nevd ....... (7) |
J = ne Or |
= = |
Resistivity ρ ρ = |
So = Also ρ = |
μ= |
J = nevd |
J = neμE Or |
 so equation (10) can be rewritten as
so equation (10) can be rewritten as = μne μ = |
λ = |
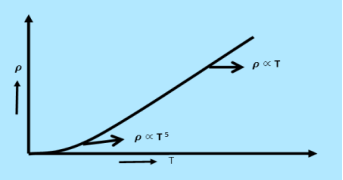
 and increases linearly with temperature T
and increases linearly with temperature T. |
λ = |
ρ = |
ρ |
|
|
vg |
E ℏ and p ℏk (2) |
|
 vanishes at the boundaries of the Brillouin zone (k= ± /a)
vanishes at the boundaries of the Brillouin zone (k= ± /a)vg |
|
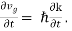 The force acting on the group of electrons is then
The force acting on the group of electrons is thenF = m |
F = |
|
|
In metals, the Fermi energy gives us information about the velocities of the electrons which participate in ordinary electrical conduction. The amount of energy which can be given to an electron in such conduction processes is on the order of micro-electron volts (see copper wire example), so only those electrons very close to the Fermi energy can participate. The Fermi velocity of these conduction electrons can be calculated from the Fermi energy.
This speed is a part of the microscopic Ohm's Law for electrical conduction. For a metal, the density of conduction electrons can be implied from the Fermi energy. |
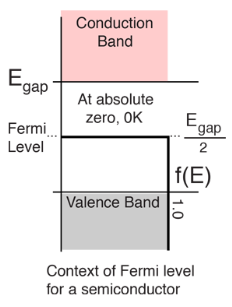
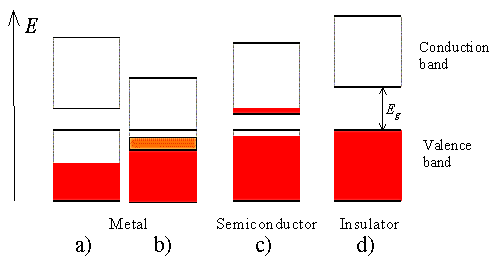
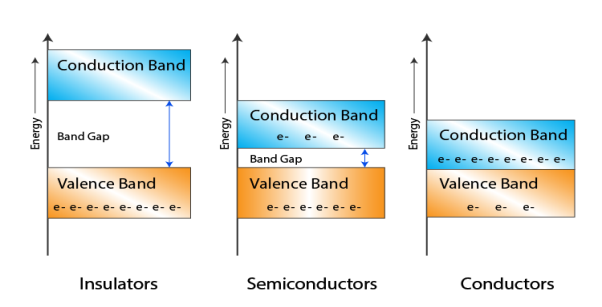
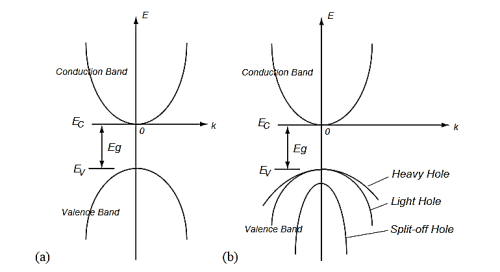
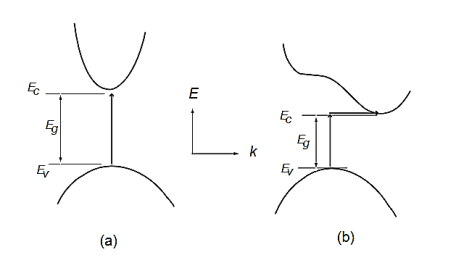
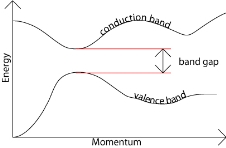
Figure 12: Fermi level for a Semiconductor
|
|
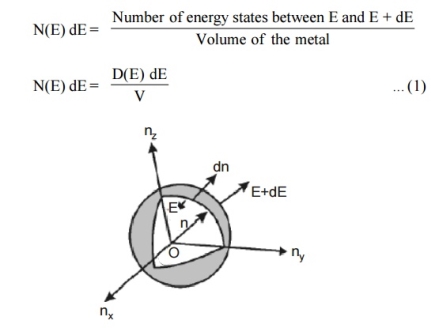
n(E) = |
|
F(E) = |
|
F(E) = |
F(E) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
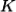 is created by inelastic scattering of a photon or neutron from wavevector
is created by inelastic scattering of a photon or neutron from wavevector 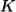 to
to 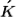 , the wavevector selection rule that governs the process is
, the wavevector selection rule that governs the process is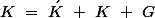 Where
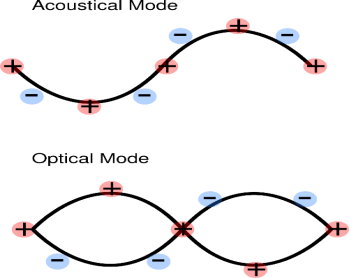
Where  is a reciprocal lattice vector ACOUSTIC PHONONS AND OPTICAL PHONONSWhen the unit cell contains more than one atom, the crystal will contain two types of phonon, acoustic and optical. Optical phonons are excited easily by light. In acoustic phonons, both positive and negative ions swing together. In optical phonons, positive and negative phonons swing against each other.
is a reciprocal lattice vector ACOUSTIC PHONONS AND OPTICAL PHONONSWhen the unit cell contains more than one atom, the crystal will contain two types of phonon, acoustic and optical. Optical phonons are excited easily by light. In acoustic phonons, both positive and negative ions swing together. In optical phonons, positive and negative phonons swing against each other.
|
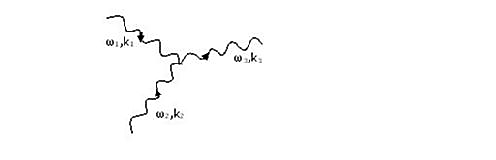
 Phonon-phonon collision
Phonon-phonon collision
|
|
|
|
|