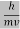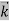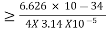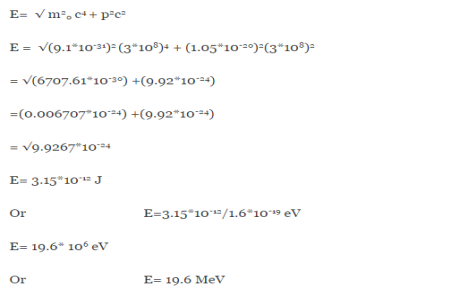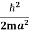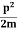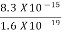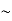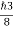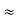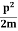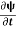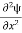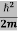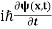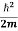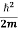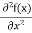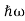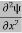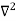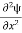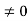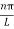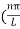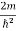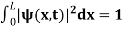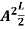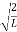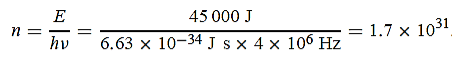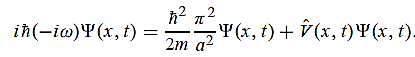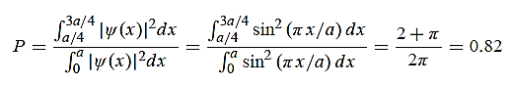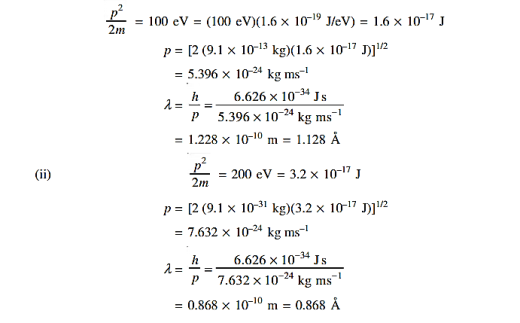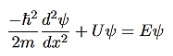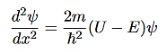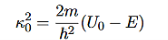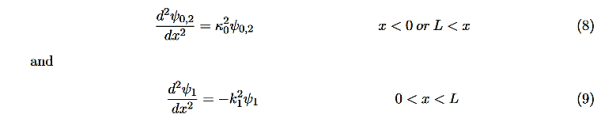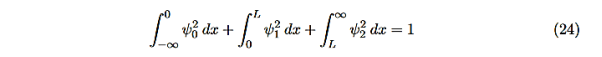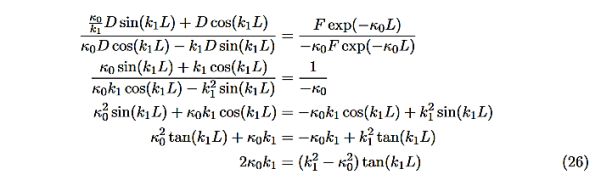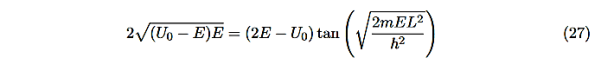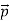 behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector  are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.λ = |
|
(a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s) p = 4.92 × 10–24 kg m/s de Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s λ= 0.135 nm (b)For the ball: Mass m’ = 0.150 kg, Speed v ’= 30.0 m/s. Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s) p’= 4.50 kg m/s de Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
|
Accelerating potential V = 100 V. The de Broglie wavelength λ is λ= h /p = 1 227/ λ.1 227/ The de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths. |
 , velocity
, velocity  , and all the forces acting on the particle are known, the position
, and all the forces acting on the particle are known, the position 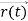 , and velocity
, and velocity 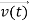 are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.Does this hold for the microphysical world? Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle. In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.Does this hold for the microphysical world? Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle. In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
Given m = 0.5kg, h = 6.626 × 10-34 m2 kg / s Δp =p×1×10−6 As we know that, Δp = 10-5 Heisenberg Uncertainty principle formula is given as, ∆x∆p ∆x ∆x ∆x =0.527 x 10-29 m |

|

|
∆x∆px = ℏ/2 or Thus ∆px= ℏ /2∆x ∆px= ℏ /2a/2 = ℏ /a Uncertainty in momentum of particle along x-axis is ∆px= ℏ /a |
K.E. = |
E = |
 ; Similarly ∆ y ∆ py =
; Similarly ∆ y ∆ py =  , And ∆ z ∆ pz =
, And ∆ z ∆ pz =  , Multiplying these three equations, we get
, Multiplying these three equations, we get ∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = ( The above product is called the volume of elementary cell in phase space. So, volume of an elementary cell in phase space
|
Thus, uncertainly in energy is ∆ E
Or ∆ E
Or ∆ E
Frequency of light is uncertain by
∆ ν = As a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ ν and ν + ∆ ν. |
E= K+V = |
ℏω =
A wave with frequency ω and wave number k can be written as usual as ψ(x, t) =Aei(kx−ωt) ……….. (3)
the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only.
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain ℏ(ωψ) = This is the time-dependent Schrodinger equation.
|
|
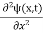 term becomes ∇2ψ. The term |ψ(x)|2 gives the probability of finding the particle at position x. Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7) But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
term becomes ∇2ψ. The term |ψ(x)|2 gives the probability of finding the particle at position x. Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7) But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
We already know that E=
Eψ = - |
Given m= 9×10–31 ΔV= 5.7×105 m/sec Δx=? h= 6.6×10–34 Joule-Sec. Δx.Δv ≥h/4πm Δx≥h/4πmΔv ≥6.6×10–34/9×3.14×9.1×10–31×5.7×105 ≥ 0.010×10–8 ≥ 1×10–10m |
m=10 gm. h=6.6×10–27 erg-sec Δv= 5.25×10–26 cm Δx=? Δx.Δv ≥h/4πm Δx≥h/4πmΔv ≥6.6×10-34/4×3.14×10×5.25×10–26 ≥ 0.10×10–2m ≥ 1×10–3 cm |
ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity. |
 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite. 0 as x
0 as x .
.
|
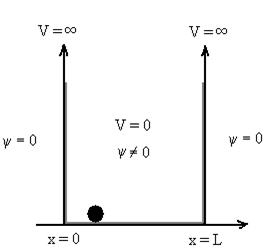
V= 0 for 0 V= |
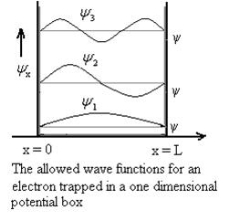
Figure : Particle in deep potential well |
Substituting
writing the SWE for 1-D we get
The general equation of above equation may be expressed as ψ = Asin (kx + ϕ) …………….(5) Where A and ϕ are constants to be determined by boundary conditions Condition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5) 0 = Asin kL As A k = where n= 1,2,3,4……… Substituting the value of k from (7) to (3)
|
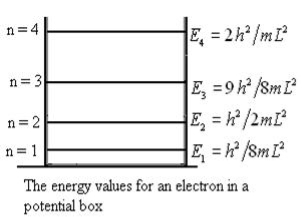
En = |
From equation En is the energy value (Eigen Value) of the particle in a well. It is clear that the energy values of the particle in well are discrete not continuous.
|
|
 1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism. Q16) Consider a one-dimensional particle which is confined within the region 0
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism. Q16) Consider a one-dimensional particle which is confined within the region 0  x
x a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4
a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4  x
x  3a/4.A16)Since the first time derivative and the second x derivative of (x, t), are given by
3a/4.A16)Since the first time derivative and the second x derivative of (x, t), are given by 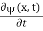 =-iω (x, t) and
=-iω (x, t) and  =- (π2/a2) (x, t) the Schrödinger equation yields
=- (π2/a2) (x, t) the Schrödinger equation yields
|
|
 x
x  3a/4.can be obtained from
3a/4.can be obtained from
|
|
|
|
|
|
U=U0 x <0 (1) U= 0 0 U=U0 L < x. (3) |
We want to solve Schroedinger’s Equation for this potential to get the wave functions and allowed energies for E < U0. We will refer to the three regions as regions 0, 1, and 2 with associated wave functions ψ0,ψ1,ψ2.
Figure 8: Finite Square Well Potential Energy The time-invariant, non-relativistic Schroedinger’s equation is
that can be rearranged to give
It is convenient to define two new variables (both positive), one for regions 0 and 2, and one for region 1—they are wavenumbers:
and Schrödinger’s equation becomes
In regions 0 and 2 the general solution is a linear combination of exponentials with the same form, but with different constants, namely
In region 1 we have the same general solution that we had for the infinite square well,
Equations (10) to (12) have 7 unknowns—A,B,C,D,F,G and the energy E that is im-plicitly contained in the variables κ0,k1. Therefore we need to get 7 equations to be ableto solve for the unknowns. We will first use the requirement that the wavefunction remain finite everywhere. Consider ψ2 as x→∞. For this to remain finite we must require G= 0. Similarly, as x→−∞, we require A= 0. Our solutions become
The next step is to require that the wavefunction and its first derivative be continuous everywhere, and in our case we look at the boundaries, x= 0 and x=L.
Hence ψ0=D exp(+κ0x).Take derivatives of the wave functions,
|
|
|
|
|
|
|
Figure : Wave function in Finite well |