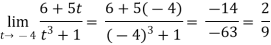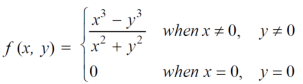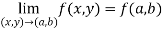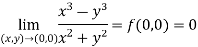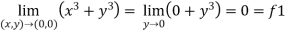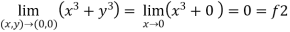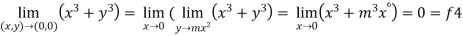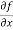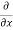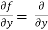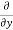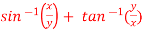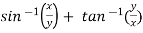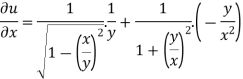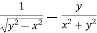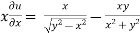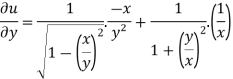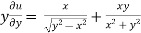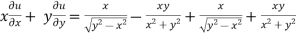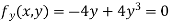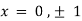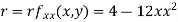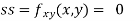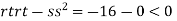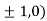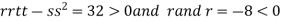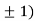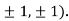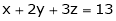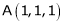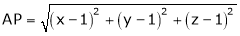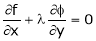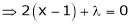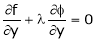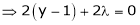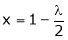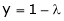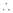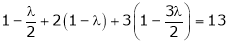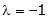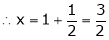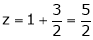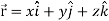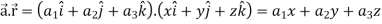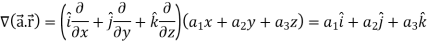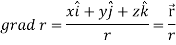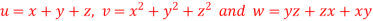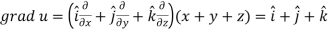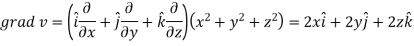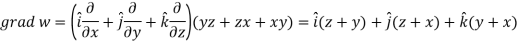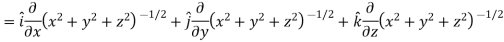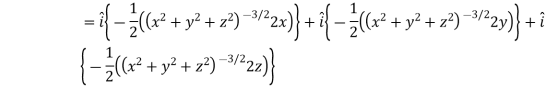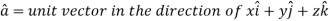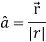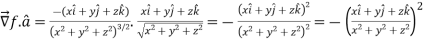 A1)
A1)We can simply find the solution as follows,
|
|
The function is well defined at (0,0) (2) check for the second step,
That means the limit exists at (0,0) Now check step-3:
So that the function is continuous at origin. |
 A3)
A3)
2. Here f1 = f2 3. now put y = mx, we get
Here f1 = f2 = f3 Now put y = mx² 4. Therefore , F1 = f2 = f3 =f4 We can say that the limit exists with 0. |
 and
and 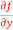 for the following functionf( x, y) = sin(y²x + 5x – 8)A4)
for the following functionf( x, y) = sin(y²x + 5x – 8)A4)To calculate
= cos(y²x + 5x – 8) = (y² + 50)cos(y²x + 5x – 8) Similarly partial derivative of f(x,y) with respect to y is,
= cos(y²x + 5x – 8) = 2xycos(y²x + 5x – 8) |
if |
Here we have, u = now partially differentiate eq.(1) w.r to x and y , we get
= Or
And now,
=
Adding eq. (1) and (3) , we get
Hence proved. |
|
Partially differentiating given equation with respect to and x and y then equate them to zero
On solving above we get Also Thus we get the pair of values (0,0), ( Now, we calculate
At the point (0,0)
So function has saddle point at (0,0). At the point (
So the function has maxima at this point ( At the point (0,
So the function has minima at this point (0, At the point (
So the function has an saddle point at ( |
 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.A7)
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.A7)Let
Under the condition
i.e.
From (2) we get From (3) we get From (4) we get
i.e.
y = 2
|
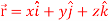 , then show that1.
, then show that1.  2.
2.  A8)
A8)Suppose
Now taking L.H.S,
Which is Hence proved.
2. So that
|
If |
Here-
Now-
Apply
Which becomes zero. So that we can say that grad u, grad v and grad w are coplanar vectors. |
 where
where  A10)
A10)Here Now,
And We know that-
So that-
Now, Directional derivative = |