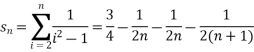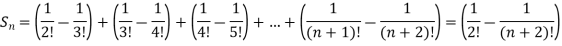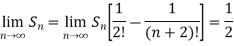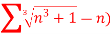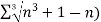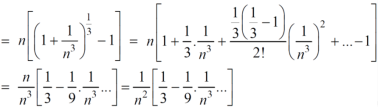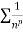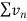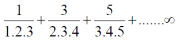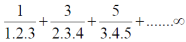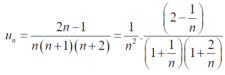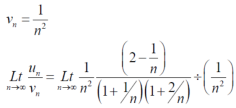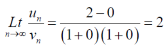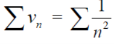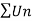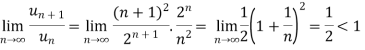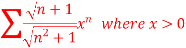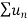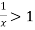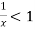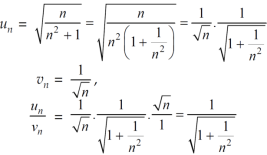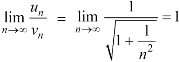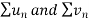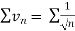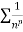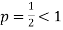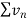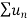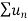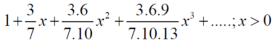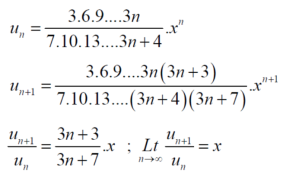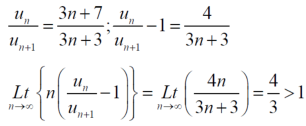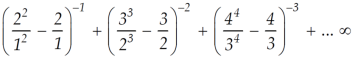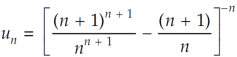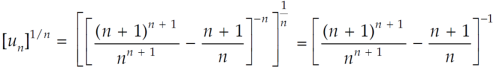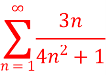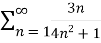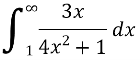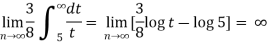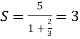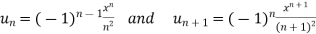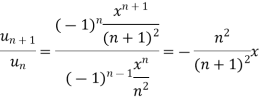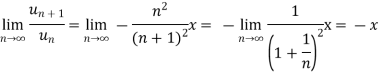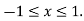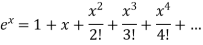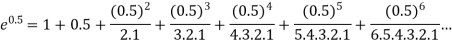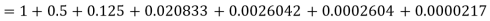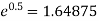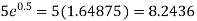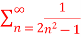The general formula can be written as,

We get on applying limits,

) = 3/4

This is the convergent series and its value is 3 / 4

Here,

And

Hence the series is convergent and the limit is 1/2.

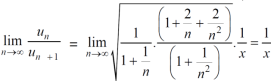
We have  

First we will find  and the

And

Here, we can see that, the limit is finite and not zero,

Therefore, and converges or diverges together.

Since is of the form  where p = 2>1

So that , we can say that,

is convergent , so that will also be convergent.

Suppose,

Which is finite and not zero.

By comparison test and converge or diverge together.

But,

Is convergent. So that is also convergent.

We have

  and

By D’Alembert ratio test,

So that by D’Alembert ratio test , the series will be convergent.

We have,

Now , by D’Almbert ratio test converges if and diverges if 

At x = 1 , this test fails.

Now , when x = 1

The limit is finite and not zero.

Then by comparison test, converges or diverges together.

Since is the form of , in which

Hence diverges then will also diverge.

Therefore in the given series converges if x<1 and diverges if x≥1.

As we will neglect the first term, we get

By ration test  is convergent when x<1 and divergent when x>1, when x= 1,

The rario test fails, then

By Rabee’s test is convergent , hence the given series is convergent when x≤ 1 and divergent If x >1.

Here, we have,

Therefore the given series is convergent.

Here is positive and decreases when we increase n ,

Now apply integral test,

Let,          

X = 1 , t = 5 and x = ∞ , t = ∞,

Now,

So by integral test,

The series is divergent.

Here the given series is alternately negative and positive , which is also a geometric infinite series.

1. suppose,

                        S = 

According to the conditions of geometric series,

Here , a = 5 , and common ratio (r) = -2/3 

Thus, we know that,

So ,

Sum of the series is finite , which is 3.

So we can say that the given series is convergent.

Now.

Again sum of the positive terms,

The series is geometric, then

A = 5 and  r = 2/3 , then

Sum of the series,

Sum of the series is finite then the series is convergent.

Both conditions are satisfied , then the given series is absolutely convergent.

Here

Then,

By D’Almbert’s ratio test the series is convergent for |x|<1 and divergent if |x|>1.

So at x = 1

The series becomes-

At x = -1

This is an alternately convergent series.

This is also convergent series, p = 2

Here, the interval of convergence is

As we know that the exponential series is-

Here we get-

Now