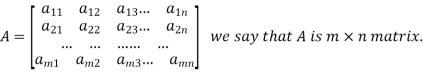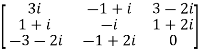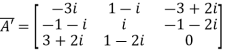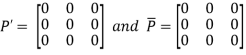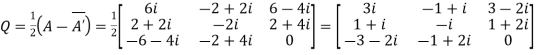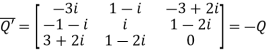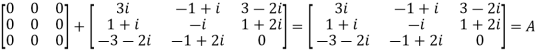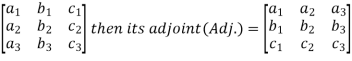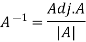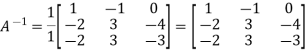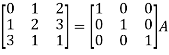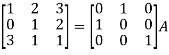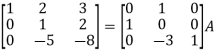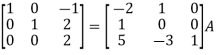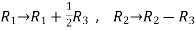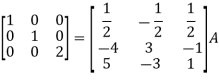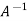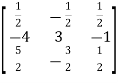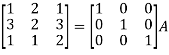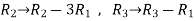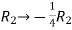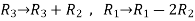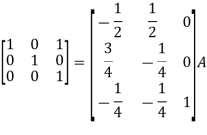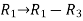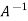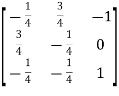BM
UNIT – IIIMatrices Q1) Explain matrices.A1) Matrices have wide range of applications in various disciplines such as chemistry, Biology, Engineering, Statistics, economics, etc. Matrices play an important role in computer science also. Matrices are widely used to solving the system of linear equations, system of linear differential equations and non-linear differential equations. First time the matrices were introduced by Cayley in 1860. Definition-A matrix is a rectangular arrangement of the numbers.These numbers inside the matrix are known as elements of the matrix.A matrix ‘A’ is expressed as-
The vertical elements are called columns and the horizontal elements are rows of the matrix.The order of matrix A is m by n or (m× n) Notation of a matrix-A matrix ‘A’ is denoted as-A =  Where, i = 1, 2, …….,m and j = 1,2,3,…….nHere ‘i’ denotes row and ‘j’ denotes column. Q2) Explain the types of matrices.A2) Types of matrices-1. Rectangular matrix-A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.Example: A =
Where, i = 1, 2, …….,m and j = 1,2,3,…….nHere ‘i’ denotes row and ‘j’ denotes column. Q2) Explain the types of matrices.A2) Types of matrices-1. Rectangular matrix-A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.Example: A = 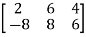 The order of matrix A is 2×3 , that means it has two rows and three columns.Matrix A is a rectangular matrix. 2. Square matrix-A matrix which has equal number of rows and columns, is called square matrix.Example:A =
The order of matrix A is 2×3 , that means it has two rows and three columns.Matrix A is a rectangular matrix. 2. Square matrix-A matrix which has equal number of rows and columns, is called square matrix.Example:A =  The order of matrix A is 3 ×3 , that means it has three rows and three columns.Matrix A is a square matrix. 3. Row matrix-A matrix with a single row and any number of columns is called row matrix.Example:A =
The order of matrix A is 3 ×3 , that means it has three rows and three columns.Matrix A is a square matrix. 3. Row matrix-A matrix with a single row and any number of columns is called row matrix.Example:A = 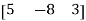 4. Column matrix- A matrix with a single column and any number of rows is called row matrix.Example:A =
4. Column matrix- A matrix with a single column and any number of rows is called row matrix.Example:A =  5. Null matrix (Zero matrix)-A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by OExample:A =
5. Null matrix (Zero matrix)-A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by OExample:A = 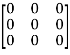 6. Diagonal matrix-A matrix is said to be diagonal matrix if all the elements except principal diagonal are zeroThe diagonal matrix always follows-
6. Diagonal matrix-A matrix is said to be diagonal matrix if all the elements except principal diagonal are zeroThe diagonal matrix always follows- 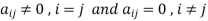 Example: A =
Example: A =  7. Scalar matrix-A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.Example-A =
7. Scalar matrix-A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.Example-A =  8. Identity matrix-A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.It is denoted by – ‘I’I =
8. Identity matrix-A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.It is denoted by – ‘I’I =  9. Triangular matrix-If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.There are two types of triangular matrices-(a) Lower triangular matrix- If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example: A =
9. Triangular matrix-If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.There are two types of triangular matrices-(a) Lower triangular matrix- If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example: A = 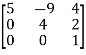 (b) Upper triangular matrix- If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example- A =
(b) Upper triangular matrix- If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example- A =  Special types of matrices-Symmetric matrix-Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.For example:
Special types of matrices-Symmetric matrix-Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.For example:  and
and 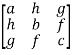 Example: check whether the following matrix A is symmetric or not?A =
Example: check whether the following matrix A is symmetric or not?A =  Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.So that, first we will find its transpose,Transpose of matrix A ,
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.So that, first we will find its transpose,Transpose of matrix A ,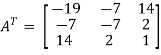 Here, A =
Here, A = 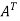 The matrix A is symmetric.Q3) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.A3) Suppose A is any square matrix.Then,A =
The matrix A is symmetric.Q3) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.A3) Suppose A is any square matrix.Then,A = 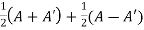 Now,(A + A’)’ = A’ + AA+A’ is a symmetric matrix.Also,(A - A’)’ = A’ – AHere A’ – A is an anti – symmetric matrixSo that,Square matrix = symmetric matrix + anti-symmetric matrix Q4) Express the matrix A as sum of hermitian and skew-hermitian matrix
Now,(A + A’)’ = A’ + AA+A’ is a symmetric matrix.Also,(A - A’)’ = A’ – AHere A’ – A is an anti – symmetric matrixSo that,Square matrix = symmetric matrix + anti-symmetric matrix Q4) Express the matrix A as sum of hermitian and skew-hermitian matrix
Q5) If A =  then show that(i)
then show that(i) 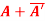 is hermitian matrix.(ii)
is hermitian matrix.(ii)  is skew-hermitian matrix. A5)Given A =
is skew-hermitian matrix. A5)Given A =  Then
Then  Let
Let  Also
Also  Hence P is a Hermitian matrix.Let
Hence P is a Hermitian matrix.Let 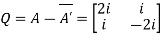 Also
Also 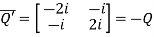 Hence Q is a skew-hermitian matrix. Q6) Explain Inverse of Matrices with examples.A6)Adjoint of a matix-Transpose of a co-factor matrix is known as the disjoint matrix.If the following is a co-factor of matrix A-
Hence Q is a skew-hermitian matrix. Q6) Explain Inverse of Matrices with examples.A6)Adjoint of a matix-Transpose of a co-factor matrix is known as the disjoint matrix.If the following is a co-factor of matrix A-
Inverse of a matrix-The inverse of a matrix ‘A’ can be find as-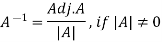 Example: Find the inverse of matrix ‘A’ if-
Example: Find the inverse of matrix ‘A’ if- Sol.Here we have-
Sol.Here we have-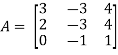 Then
Then  And the matrix formed by its co-factors of |A| is-
And the matrix formed by its co-factors of |A| is- Then
Then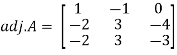 Therefore-We know that-
Therefore-We know that-
Inverse of a matrix by using elementary transformation-The following transformation are defined as elementary transformations-1. Interchange of any two rows (column) 2. Multiplication of any row or column by any non-zero scalar quantity k.3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.The symbol ~ is used for equivalence.Q7) Find the inverse of matrix ‘A’ by using elementary transformation-A =  A7)
A7)
Q8) Find the inverse of matrix ‘A’ by using elementary transformation-A = 
Q9) Explain system of linear equations and its applications with examples.A9) Equations of the form ax+b=0 are called linear equations in the variable x. In this section we will be concerned with the problem of solving linear equations, and equations that reduce to linear equations. We define two equations as equivalent if they have the same solution set. The following two operations on an equation always result in a new equation which is equivalent to the original one. These operations, sometimes called elementary transformations, are: T.1 The same expression representing a real number may be added to both sides of an equation. T.2 The same expression representing a nonzero real number may be multiplied into both sides of an equation. Using these operations, we may transform an equation whose solution set is not obvious through a series of equivalent equations to an equation that has an obvious solution set. Example 1. Solve the equation (a) 2 x-3=4+x Add − x to both sides to obtain − x+2 x-3=− x+4+x (T.1) or x-3=4 Add 3 to both sides to obtain x-3+3=4+3 (T.1) or x=7 Since 2 x-3=4+x is equivalent to x-3=4, which, in turn, is equivalent to x=7, whose solution set is obviously {7}, we know that the solution set of (a) is {7}. Example 2. Solve the equation (b) 12 x+23=52 x-1 Add − (12) x to both sides to obtain 23=52 x-12 x-1 (T.1) or 23=2 x-1 Add 1 to both sides to obtain 1+23=2 x (T.1) or 53=2 x Multiply both sides by 12 to obtain 56=x (T.2) Thus, the solution set of (b) is {56}. Every linear equation can be solved in the same way as in the above examples. In fact, let us consider the general linear equation ax+b=0 Add − b to both sides to obtain ax=− b Multiply both sides by 1a to obtain x=− (ba) if a a≠0. The general linear equation, therefore, has as its solution set {ba}, if a≠0. Thus each linear equation has at most one solution. The next two examples are of equations that reduce to linear equations. Example 3. Solve the equation 23+4 y (5 y+4)=9+10 y (2 y+3) We expand both sides to obtain 23+20 y2+16 y=9+20 y2+30 y Add − 20 y2 to both sides to obtain 23+16 y=9+30 y We now solve as in the previous examples. 23+16 y=9+30 y 23-9=30 y-16 y 14=14 y y=1 Thus, the solution set is {1}. Example 4. Solve the equation (c) 2 xx-1=2x-1+1 The replacement set of (c) is all real numbers except 1. Assuming that x≠1, we multiply both sides of (c) by x-1 to obtain (d) 2 x=2+x-1, x≠1 Solving the equation 2 x=2+x-1, we obtain 1 as the only solution Since 1 is not in the replacement of (d), (d) has no solution. Furthermore, (c) is equivalent to (d), therefore (c) has no solution. Q10) If 2 times a certain integer is added to the next consecutive integer the result is 34. Find the integers.
A10) Let x be the first integer.
Then x+1 is the next consecutive integer.
2 times a certain integer plus the next consecutive integer is 34.
Then, 2 x+(x+1) =34 3 x+1=343 x=33x=11Check. 2·11+(11+1)=34 Q11) Bob and Joe together earned $60. Both were paid at the same rate, but Bob worked three times as long as Joe. How much did each receive?A11)Let x be the number of dollars that Joe received.Then 3 x is the number of dollars that Bob receivedBob and Joe together earned $60.3 x+x=604 x=60x=153 x=45Check 3·15+15=60 Q12) The sum of the digits of a two-digit number is 12. If the digits are reversed the number is decreased by 36. What is the number?A12)Let x be the tens digit.Then 12-x is the unit’s digit.If the digits are reversed then the number is decreased by 36Then, 10 (12-x)+x=10 x+(12-x)-36 =120-10 x+x=10 x+12-x-36 =120-9 x=9 x-24 =144=18 x =x=8 =12-x=4 Therefore, the number is84. Check. 84-36=48 Q13) How many pounds of candy valued at 48¢ per pound should be added to 50 pounds of candy valued at 80¢ per pound in order for the store owner to be able to sell the candy at 60¢ per pound?
A13) Let x be the number of pounds of 48¢ per pound candy.
Then 50+x would be the pounds of candy he would have at 60¢ per pound.
The amount of candy at 48¢ per pound times 48¢, plus the amount of candy at 80¢ per pound times 80¢, must be equal to the amount of candy at 60¢ per pound times 60¢.
(48¢/lb)(x lbs) + (80¢/lb) (50 lbs) = (60¢/lb) [(50+x)lbs]Then, 48 x+80·50=60 (50+x) 48 x+4000=3000+60 x 1000=12 x x=(83 13)lbs Check. (83+13) 48+80·50=60 (50+83+13) Problems involving velocities (or speeds) will use the formula d=rt where d is the distance travelled, r is the rate, and t is the time. When the formula is used, d and r must be expressed in the same unit of distance, while r and t must be expressed in the same unit of time. Q14) A group of students drove to a lake in the north woods to fish. They travelled 380 miles in 7 hours, of which 4 hours were on a paved highway and the remaining time was on a dirt road. If the average speed on the dirt road was 25 miles per hour less than the average speed on the highway, then find for each part of the trip the average speed and the distance travelled.A14)Let x be the speed on the dirt road.Then x+25 is the speed on the highway.The distance travelled on the highway plus the distance travelled on the dirt road is equal to 380 miles.Since d=rt, we have [(x+25) mihr] (4 hrs)+[x mihr] (3 hrs)=380 mi (x+25) 4+3 x=380 4 x+100+3 x=380 7 x=280 x=40 miles per hour x+25=65miles per hour Check. (40+25) 4+40·3=380 Work problems which involve the rate of performance can often be solved by first finding the fractional part of the task done by each person or machine in one unit of time, and then finding an equation that relates these various fractional parts.
|
 Where, i = 1, 2, …….,m and j = 1,2,3,…….nHere ‘i’ denotes row and ‘j’ denotes column. Q2) Explain the types of matrices.A2) Types of matrices-1. Rectangular matrix-A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.Example: A =
Where, i = 1, 2, …….,m and j = 1,2,3,…….nHere ‘i’ denotes row and ‘j’ denotes column. Q2) Explain the types of matrices.A2) Types of matrices-1. Rectangular matrix-A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.Example: A = 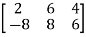 The order of matrix A is 2×3 , that means it has two rows and three columns.Matrix A is a rectangular matrix. 2. Square matrix-A matrix which has equal number of rows and columns, is called square matrix.Example:A =
The order of matrix A is 2×3 , that means it has two rows and three columns.Matrix A is a rectangular matrix. 2. Square matrix-A matrix which has equal number of rows and columns, is called square matrix.Example:A =  The order of matrix A is 3 ×3 , that means it has three rows and three columns.Matrix A is a square matrix. 3. Row matrix-A matrix with a single row and any number of columns is called row matrix.Example:A =
The order of matrix A is 3 ×3 , that means it has three rows and three columns.Matrix A is a square matrix. 3. Row matrix-A matrix with a single row and any number of columns is called row matrix.Example:A = 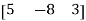 4. Column matrix- A matrix with a single column and any number of rows is called row matrix.Example:A =
4. Column matrix- A matrix with a single column and any number of rows is called row matrix.Example:A =  5. Null matrix (Zero matrix)-A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by OExample:A =
5. Null matrix (Zero matrix)-A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by OExample:A = 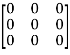 6. Diagonal matrix-A matrix is said to be diagonal matrix if all the elements except principal diagonal are zeroThe diagonal matrix always follows-
6. Diagonal matrix-A matrix is said to be diagonal matrix if all the elements except principal diagonal are zeroThe diagonal matrix always follows- 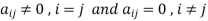 Example: A =
Example: A =  7. Scalar matrix-A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.Example-A =
7. Scalar matrix-A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.Example-A =  8. Identity matrix-A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.It is denoted by – ‘I’I =
8. Identity matrix-A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.It is denoted by – ‘I’I =  9. Triangular matrix-If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.There are two types of triangular matrices-(a) Lower triangular matrix- If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example: A =
9. Triangular matrix-If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.There are two types of triangular matrices-(a) Lower triangular matrix- If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example: A = 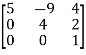 (b) Upper triangular matrix- If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example- A =
(b) Upper triangular matrix- If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.Example- A =  Special types of matrices-Symmetric matrix-Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.For example:
Special types of matrices-Symmetric matrix-Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.For example:  and
and 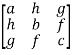 Example: check whether the following matrix A is symmetric or not?A =
Example: check whether the following matrix A is symmetric or not?A =  Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.So that, first we will find its transpose,Transpose of matrix A ,
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.So that, first we will find its transpose,Transpose of matrix A ,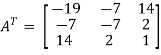 Here, A =
Here, A = 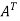 The matrix A is symmetric.Q3) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.A3) Suppose A is any square matrix.Then,A =
The matrix A is symmetric.Q3) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.A3) Suppose A is any square matrix.Then,A = 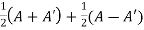 Now,(A + A’)’ = A’ + AA+A’ is a symmetric matrix.Also,(A - A’)’ = A’ – AHere A’ – A is an anti – symmetric matrixSo that,Square matrix = symmetric matrix + anti-symmetric matrix Q4) Express the matrix A as sum of hermitian and skew-hermitian matrix
Now,(A + A’)’ = A’ + AA+A’ is a symmetric matrix.Also,(A - A’)’ = A’ – AHere A’ – A is an anti – symmetric matrixSo that,Square matrix = symmetric matrix + anti-symmetric matrix Q4) Express the matrix A as sum of hermitian and skew-hermitian matrix A4) where
Let A = Therefore Let Again Hence P is a hermitian matrix. Let Again Hence Q is a skew- hermitian matrix. We Check P +Q= Hence proved. |
 then show that(i)
then show that(i) 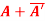 is hermitian matrix.(ii)
is hermitian matrix.(ii)  is skew-hermitian matrix. A5)Given A =
is skew-hermitian matrix. A5)Given A =  Then
Then  Let
Let  Also
Also  Hence P is a Hermitian matrix.Let
Hence P is a Hermitian matrix.Let 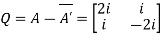 Also
Also 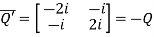 Hence Q is a skew-hermitian matrix. Q6) Explain Inverse of Matrices with examples.A6)Adjoint of a matix-Transpose of a co-factor matrix is known as the disjoint matrix.If the following is a co-factor of matrix A-
Hence Q is a skew-hermitian matrix. Q6) Explain Inverse of Matrices with examples.A6)Adjoint of a matix-Transpose of a co-factor matrix is known as the disjoint matrix.If the following is a co-factor of matrix A-
|
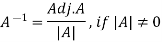 Example: Find the inverse of matrix ‘A’ if-
Example: Find the inverse of matrix ‘A’ if- Sol.Here we have-
Sol.Here we have-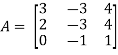 Then
Then  And the matrix formed by its co-factors of |A| is-
And the matrix formed by its co-factors of |A| is- Then
Then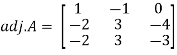 Therefore-We know that-
Therefore-We know that-
|
 A7)
A7) Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
Apply
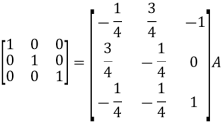
So that,
|

A8) Write the matrix ‘A’ as- A = IA
Apply
Apply
Apply
Apply
So that
|
A10) Let x be the first integer.
Then x+1 is the next consecutive integer.
2 times a certain integer plus the next consecutive integer is 34.
Then, 2 x+(x+1) =34 3 x+1=343 x=33x=11Check. 2·11+(11+1)=34 Q11) Bob and Joe together earned $60. Both were paid at the same rate, but Bob worked three times as long as Joe. How much did each receive?A11)Let x be the number of dollars that Joe received.Then 3 x is the number of dollars that Bob receivedBob and Joe together earned $60.3 x+x=604 x=60x=153 x=45Check 3·15+15=60 Q12) The sum of the digits of a two-digit number is 12. If the digits are reversed the number is decreased by 36. What is the number?A12)Let x be the tens digit.Then 12-x is the unit’s digit.If the digits are reversed then the number is decreased by 36Then, 10 (12-x)+x=10 x+(12-x)-36 =120-10 x+x=10 x+12-x-36 =120-9 x=9 x-24 =144=18 x =x=8 =12-x=4 Therefore, the number is84. Check. 84-36=48 Q13) How many pounds of candy valued at 48¢ per pound should be added to 50 pounds of candy valued at 80¢ per pound in order for the store owner to be able to sell the candy at 60¢ per pound?
A13) Let x be the number of pounds of 48¢ per pound candy.
Then 50+x would be the pounds of candy he would have at 60¢ per pound.
The amount of candy at 48¢ per pound times 48¢, plus the amount of candy at 80¢ per pound times 80¢, must be equal to the amount of candy at 60¢ per pound times 60¢.
(48¢/lb)(x lbs) + (80¢/lb) (50 lbs) = (60¢/lb) [(50+x)lbs]Then, 48 x+80·50=60 (50+x) 48 x+4000=3000+60 x 1000=12 x x=(83 13)lbs Check. (83+13) 48+80·50=60 (50+83+13) Problems involving velocities (or speeds) will use the formula d=rt where d is the distance travelled, r is the rate, and t is the time. When the formula is used, d and r must be expressed in the same unit of distance, while r and t must be expressed in the same unit of time. Q14) A group of students drove to a lake in the north woods to fish. They travelled 380 miles in 7 hours, of which 4 hours were on a paved highway and the remaining time was on a dirt road. If the average speed on the dirt road was 25 miles per hour less than the average speed on the highway, then find for each part of the trip the average speed and the distance travelled.A14)Let x be the speed on the dirt road.Then x+25 is the speed on the highway.The distance travelled on the highway plus the distance travelled on the dirt road is equal to 380 miles.Since d=rt, we have [(x+25) mihr] (4 hrs)+[x mihr] (3 hrs)=380 mi (x+25) 4+3 x=380 4 x+100+3 x=380 7 x=280 x=40 miles per hour x+25=65miles per hour Check. (40+25) 4+40·3=380 Work problems which involve the rate of performance can often be solved by first finding the fractional part of the task done by each person or machine in one unit of time, and then finding an equation that relates these various fractional parts.
0 matching results found