Unit – 3
Magneto Statics
Q1) Find the incremental field strength at P2 due to the current element of 2πa2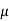 Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
A1)
The two points P1 and P2 along with the I1dL1 current element at I1 are shown in figure.
According to Bio-Savart law

d  = I1 d
= I1 d  x
x  R12 / 4 π R 2 12
R12 / 4 π R 2 12
 = (0-4)
= (0-4) 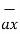 + (3-0) ay + 0. Az
+ (3-0) ay + 0. Az
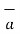 R12 =
R12 = 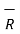 12 /|
12 /| 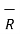 12 |
12 |
= -4  x + 3
x + 3 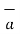 y /
y /  16 + 9
16 + 9
= -4  x + 3
x + 3 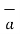 y /5
y /5
While I1 dL1 = 2
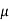 A m.
A m.
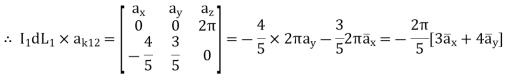
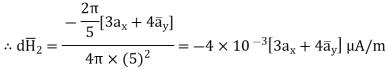
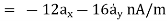
Q2) The following four vector fields are given in Cartesian co-ordinate system. The vector field, which does not satisfy the property of magnetic flux density, is
(a) 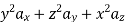

(c) 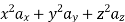

A2)
As we know that divergence of magnetic field is zero, therefore B=0
For  the above relation becomes
the above relation becomes

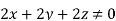
From the given options, option(c) does not satisfy the above relation.
Hence the correct option is (c)
Q3) The plane y=1 carries current density  Find H at A(0,0,0) and B(1,5,-2) .
Find H at A(0,0,0) and B(1,5,-2) .
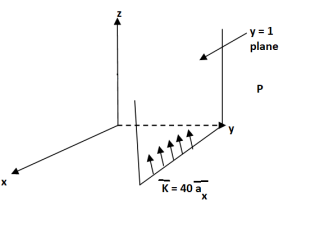
A3)
a) Pint A(0,0,0)
Normal to current sheet at point A.
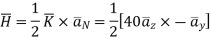
Now 
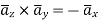

b) Point B(1,5,-2)
This is to the right of the plane as y=5 for B.
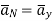 normal to sheet at point B
normal to sheet at point B

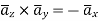
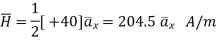
Q4) In the region 0<r<0.5m in cylindrical co-ordinates the current density is  and J=0 elsewhere. Use Amperes circuital law to find
and J=0 elsewhere. Use Amperes circuital law to find 
A4)
The current from current density is given by
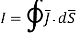
 normal to
normal to  as
as  is in
is in 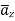
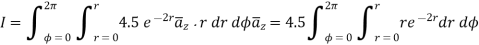
Using integration by parts

=4.5(2π)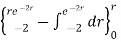


For r=0.5, I=7.608[1-0.3678-0.3678]=1.8676 A
Q5) In the region 0<r<0.5m in cylindrical co-ordinates the current density is  and J=0 else where. Use Amperes circuital law to find
and J=0 else where. Use Amperes circuital law to find 
A5)
The current from current density is given by

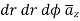 normal to
normal to 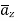 as
as  is in
is in 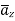

Using integration by parts

=4.5(2π)
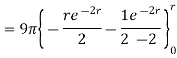
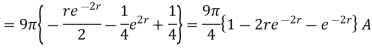
For r=0.5, I=7.608[1-0.3678-0.3678]=1.8676 A
Consider a closed path with r ≥ 0.5 such that the enclosed current I is 1.876 A.
According to Ampere’ circuital law,
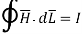
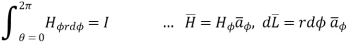
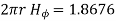

 for r
for r
Q6) A ‘z’ directed current distribution is given by
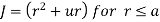 . Find
. Find 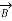 at any point using Amper’s circuital law.
at any point using Amper’s circuital law.
A6)

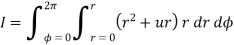
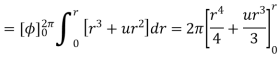
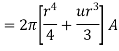
Consider a closed path with 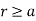 which is Amperian path.
which is Amperian path.
 while
while 
According to ampere’s circuital law
 as path has r
as path has r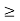 a, it encloses total I.
a, it encloses total I.
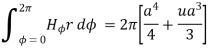

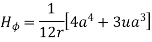

Assuming permeability of medium as

Q7) A radial field  = 2.39 x 10 6 / r cos
= 2.39 x 10 6 / r cos  A/m exists in free space. Find the magnetic flux crossing the surface defined by 0 ≤
A/m exists in free space. Find the magnetic flux crossing the surface defined by 0 ≤ ≤ π/4 and 0 ≤ z ≤ 1m.
≤ π/4 and 0 ≤ z ≤ 1m.
A7)
The portion of the cylinder is shown in figure. The flux crossing the given surface is given by
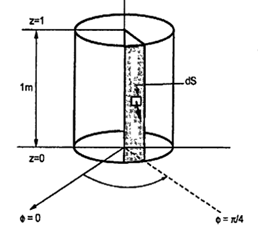
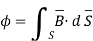
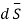 normal to
normal to 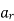 direction is,
direction is,

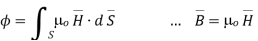
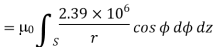
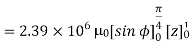
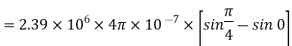
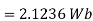
Q8) Find the flux passing the portion of the plane 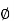 = π / 4 defined by 0.01 < r < 0.05m and 0<z<2 m. A current filament of 2.5 A is along z-axis in the
= π / 4 defined by 0.01 < r < 0.05m and 0<z<2 m. A current filament of 2.5 A is along z-axis in the 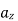 direction in free surface.
direction in free surface.

A8)
Due to current carrying conductor in free space along z-axis
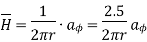
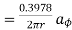 A/m
A/m
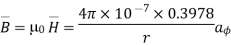
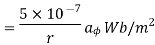
The flux crossing the surface is given by
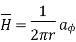


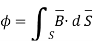
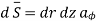 normal to
normal to  direction
direction
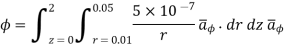

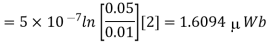
Q9) The plane of a circular coil is horizontal. It has 10 turns each of 8 cm radius. A current of 2 A flows through it, which appears clock wise from a point vertically above it. Find the magnitude and direction of the magnetic field at the centre of the coil due to current.
A9)
Here, n=10, I=2A
r= 8cm = 0.08 m
Magnitude of magnetic field induction at the centre of the circular coil carrying current is
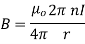
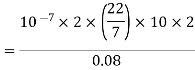
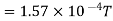
Q10) A long straight solid metal road of radius 4 cm carries a current 2A uniformly distributed over its circular cross section. Find the magnetic field induction of a distance 3 cm from the axis of wire.
A10)
The point P is lying inside the rod at perpendicular distance (r=3cm) from the axis of wire. Draw a circular closed path of radius r with centre on axis of rod such that the point P lies on this closed path.
Current enclosed by closed path
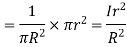
The magnetic field produced due to current flowing in the rod at every pointover the closed path is tangential to it and is equal in magnitude at all points of path.
Line integral of  over closed path is
over closed path is
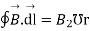
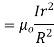
Or,
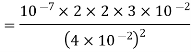

Q11) Determine the magnetic flux density B distance d meter from infinite straight wire carrying current I.
A11)
Let P be the point where B is to be evaluated consider an element it yr=dl of infinite wire shown in figure 1 tattoo distance r from point P.
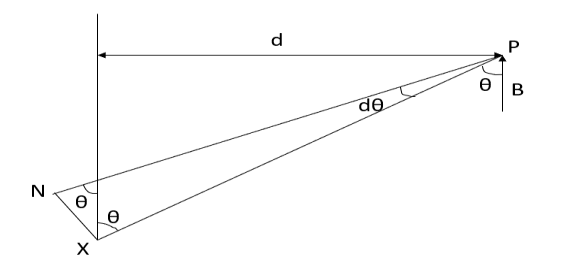
Figure: An infinite wire carrying a current I
Magnetic field B at P due to element dl from equation is given by
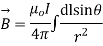
We see that
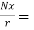 d
d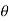
Therefore, 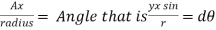
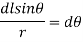
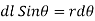
Substituting their values in above expression we have
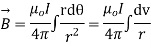




Q12) Compute curl A if .
.
A12)
Given that
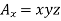
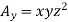
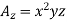
Partial derivatives will be
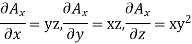


Putting these values of partial derivations in in equation


Q13) Verify that the vector field is both irrational (π has zero curl) and solenoid (π has zero divergence)
is both irrational (π has zero curl) and solenoid (π has zero divergence)
A13)
(i) given that

The partial derivatives will be
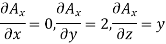

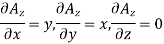
Putting these values of partial derivatives in curl equation

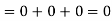
Hence the given field A is irrational since its curl zero
(ii) substituting the above calculated value of partial derivatives
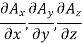
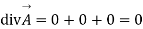
Hence the given field is solenoid since divergence is zero.
Q14) Find the work done by the force vector  .
.
Around the closed path as shown in figure.
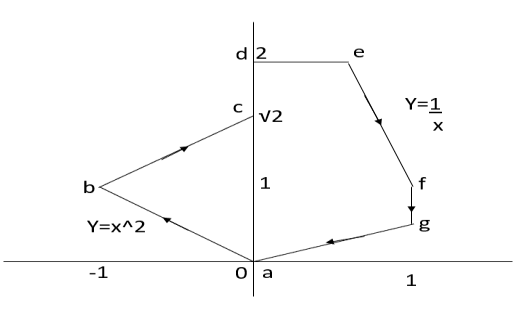
A14)
The total work done by the force vector is
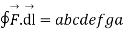
The integrals consists of 7 parts which can be calculated separately


This problem can be solved by Stokes theorem.
According two stokes theorem, the work done by force vector is
 where S is surface bounded by the closed path and F is the given force vector for this force vector the curl is equal to
where S is surface bounded by the closed path and F is the given force vector for this force vector the curl is equal to
Choose normal vector
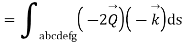

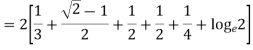

Q15) Find the curl of magnetic field and show that it is proportional to the current density.

Figure. Cross section of cylindrical conductor
A15)
For the cylindrical coordinates

But is entirely in the Q directions
is entirely in the Q directions
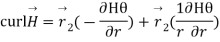
The variation of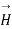 is along r axis
is along r axis
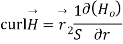
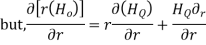



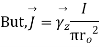

Which is proportional to J.
Q16) Calculate the magnetic flux density due to coil 100 ampere turn and area of  on the axis of coil at a distance 10 metre from the centre and at a point distance 10 metres in a direction at right angle to axis.
on the axis of coil at a distance 10 metre from the centre and at a point distance 10 metres in a direction at right angle to axis.
A16)
B on the axis of the coil

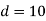

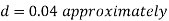

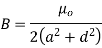
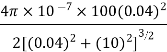

(ii) B ad perpendicular to axis
B at any point ( ) is given by
) is given by

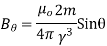

M- Magnetic moment of a current loop and is equal to 

When
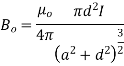
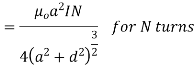

Putting the given values we have


Q17) Circuit carrying a current of I ampere from a regular polygon of n side inscribed in circumscribing circle of radius R. Calculate the magnetic flux density at the centre of the polygon and show that for a circular loop if n tends to infinity.
A17)
Since the given regular polygon has n sides

P is perpendicular chopped from centre to the sides AB and OAB is an equilateral triangle.


B due to AB is given by






 due to regular polygon of n sides will be
due to regular polygon of n sides will be

When n tends to




 at the centre of the circular loop of radius R.
at the centre of the circular loop of radius R.
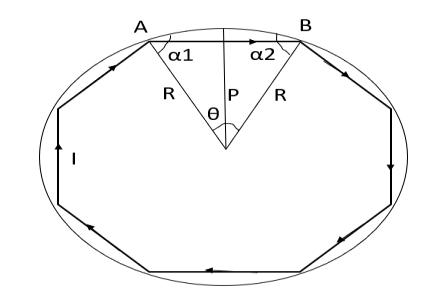
Figure: Regular polygon inscribed in a circle of radius R.
Q18) What is magnetic flux density?
A18) The magnetic flux density B is similar to the electric flux density D. As D =  in free space, the magnetic flux density B is related to the magnetic field intensity H as:
in free space, the magnetic flux density B is related to the magnetic field intensity H as:
B = ……..(1)
……..(1)
Where  is a constant known as the permeability of free space. The constant is in henrys per meter (H/m) and has the value of
is a constant known as the permeability of free space. The constant is in henrys per meter (H/m) and has the value of
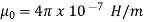
The magnetic Flux through a surface S is given by:
 …….(2)
…….(2)
Where the magnetic flux  ' is in webers (Wb) and the magnetic flux density is in webers per square meter (Wb/m2) or Tesla’s (T).
' is in webers (Wb) and the magnetic flux density is in webers per square meter (Wb/m2) or Tesla’s (T).
Unlike electric flux lines, magnetic flux lines always close upon themselves. This is because it is not possible to have isolated magnetic poles (or magnetic charges).
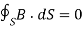 ……….(3)
……….(3)
This equation is referred to as the law of conservation of magnetic flux or Gauss's law for magnetostatic fields. Although the magnetostatic field is not conservative, magnetic flux is conserved.
By applying Divergence Theorem to equation 3, we obtain:
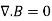 ………..(4)
………..(4)
This equation is the fourth Maxwell's equation. It also shows that magnetostatic fields have no sources or sinks. It means that magnetic field lines are always continuous.
Q19) Explain amperes circuit law?
A19) Gauss’s Law is useful to obtain  in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
It states that
The line integral of magnetic field intensity  around closed path is exactly equal to direct current enclosed by that path.
around closed path is exactly equal to direct current enclosed by that path.
The mathematical representation of Ampere’s circuital law is
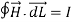 ---------------------(1)
---------------------(1)
This law is useful to determine 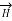 when current distribution is symmetrical.
when current distribution is symmetrical.
Proof:
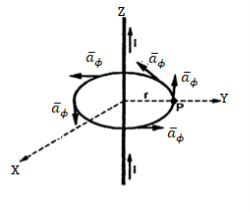
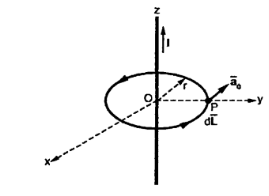
Consider a long straight conductor carrying direct current I placed along z axis as shown in figure. Consider a closed circular path of radius r which encloses the straight conductor carrying direct current I. The point P is at perpendicular distance r from the conductor.
Consider 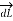 at point P which is direction
at point P which is direction 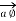 direction tangential to circular path at point P.
direction tangential to circular path at point P.
Therefore,
 (2)
(2)
While 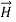 obtained at point P, from Biot-Savart law due to infinitely long conductor is,
obtained at point P, from Biot-Savart law due to infinitely long conductor is,

= 1/ 2  r . dɸ = 1/ 2 π . dɸ
r . dɸ = 1/ 2 π . dɸ
Integrating 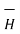 .
. 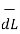 over the entire closed path
over the entire closed path
 .
.  =
=  dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
This proves that the integral 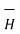 .
.  along closed path gives the direct current enclosed by that closed path.
along closed path gives the direct current enclosed by that closed path.
Steps to Apply Amper’s Circuital Law:
Step1: Consider a closed path preferably symmetrical such that it encloses the direct current I once. This is Amperian path.
Step2: Consider differential length 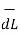 depending upon the co-ordinate system used.
depending upon the co-ordinate system used.
Step3: Identify the symmetry and find in which direction  exists according to co-ordinate system used.
exists according to co-ordinate system used.
Step 4: Find  .
. 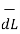 . Make sure that
. Make sure that 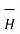 and
and  are in the same direction.
are in the same direction.
Step 5: Find the integral of  .
.  around the closed path. And equate it to current I enclosed by the path.
around the closed path. And equate it to current I enclosed by the path.
To apply Ampere’s circuital law the following conditions must be satisfied,
- The
 ie either tangential or normal to the path, at each point of the closed path.
ie either tangential or normal to the path, at each point of the closed path. - The magnitude of
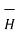 must be same at all points of the path where
must be same at all points of the path where  is tangential.
is tangential.
 due to straight conductors
due to straight conductors
Consider an infinitely long straight conductor which is placed along z-axis carrying direct current I as shown in figure. Consider the Amperian closed path enclosing the conductor as shown in figure. Consider point P on the closed path at which  is obtained. The radius of the path is r from the conductor. The magnitude of
is obtained. The radius of the path is r from the conductor. The magnitude of  depends on r and the direction is always tangential to the closed path. So,
depends on r and the direction is always tangential to the closed path. So,  has only component in
has only component in 
 direction say H
direction say H  .
.
Consider elementary length  at point P in cylindrical co-ordinates it is r d
at point P in cylindrical co-ordinates it is r d in
in  .
.
 = Hɸ
= Hɸ 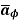 and
and  = r dɸ .
= r dɸ .
 .
. 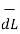 = Hɸ
= Hɸ 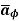 . r dɸ .
. r dɸ .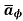 = Hɸ r dɸ
= Hɸ r dɸ
According to Ampere’s circuit law,
 = I
= I
 ɸ . r. dɸ = I
ɸ . r. dɸ = I
Hɸ . r  . dɸ = I
. dɸ = I
Hɸ . r [2π] =I
Hɸ = 1/ 2π r
Hence 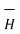 at point P is given by
at point P is given by
 = Hɸ.
= Hɸ.  = 1/ 2 π r .
= 1/ 2 π r . 
Q20) Derive all four maxwells equation?
A20) Ampere's circuit law states that the line integral of H around a closed path is the same as the net current Ienc enclosed by the path.
In other words, it can be said that the circulation of H equals Ienc:
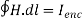 …. (1)
…. (1)
Ampere's law is similar to Gauss's law, since Ampere's law is easily applied to determine H when the current distribution is symmetrical.
Ampere’s law is a special case of Biot-Savart’s Law, it can be derived from Biot-Savart’s Law.
By applying Stokes's theorem to the left-hand side of equation 1, we get:
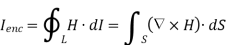
But
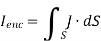
If we compare the two surface integrals, then:
 …….(2)
…….(2)
This is the third Maxwell Equation; it is essentially Ampere's law in differential
Form, whereas eq. 1 is the integral form.
Also, in Eq. 2  ; that is a magnetostatic field is not conservative.
; that is a magnetostatic field is not conservative.
For time varying Magnetic Fields, (2) is written as:
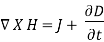
The term 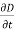 is known as displacement current density.
is known as displacement current density.