Unit - 4
Computer Arithmetic
Q1) Describe addition and subtraction algorithm?
A1) The magnitude of the two numbers is denoted by the letters A and B. There are eight different requirements to consider when signed numbers are added or subtracted, depending on the sign of the numbers and the operation done. Table's first column has a list of these requirements. The table's other columns depict the actual procedure to be carried out, together with the size of the figures. To exhibit a negative zero, the last column is required. In other words, the outcome of subtracting two equal values should be +0, not -0.
The addition and subtraction methods are obtained from the table and are as follows(the words parentheses should be used for the subtraction algorithm).
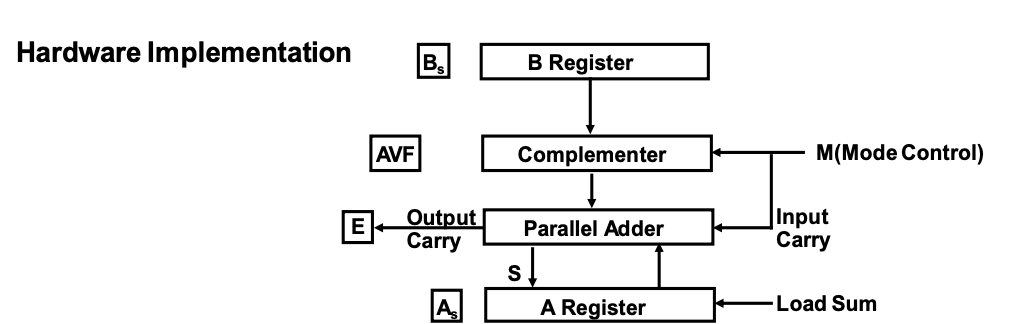
Fig 1: Signed Magnitude Addition and Subtraction and hardware implementation

Fig 2: 2’s complements addition and subtraction
Algorithm
● Figure depicts the flowchart. An exclusive-OR gate compares the two indicators A and B.
○ The signs are identical if the gate output is 0; if it is 1, the signals are different.
● The magnitudes must be added in an add operation because the signs are same. Different signs demand that the magnitudes be added in a subtract operation.
● The magnitudes are combined using the EA A + B micro operation, where EA is a register that combines E and A. If the carry in E after the addition is equal to 1, it is an overflow. In the add-overflow flip-flop AVF, the value of E is transferred.
● If the signs are different for an add operation or identical for a subtract operation, the two magnitudes are subtracted. By adding A to the 2's complementing B, the magnitudes are removed. If the numbers are removed, there will be no overflow and AVF will be cleared to 0.
● The value in A is the right answer, while 1 in E shows that A >= B. To avoid a negative zero, the sign A must be made positive if this numbs is zero.
● E with a value of 0 denotes that A is greater than B. It is essential to take the 2's complement of the value in A in this scenario. One micro action, A A' +1, is all that is required to complete the operation.
● We presume, however, that the A register comprises circuits for complement and increment micro operations, thus the 2's complement is produced from these two micro operations.
● The sign of the result in other flowchart pathways is the same as the sign of A, thus there is no need to modify A. When A B, however, the result's sign is the complement of A's initial sign. The correct sign must then be obtained by complementing A.
● The ultimate result may be found in register A, and its sign can be found in register As. Overflow is indicated by the value in AVF. It makes no difference what E's final value is.
● A block diagram of the hardware for performing addition and subtraction operations is shown in Figure 1.
○ It comprises of registers A and B, as well as As and Bs sign flip-flops.
○ Subtraction is accomplished by multiplying A by B's 2's complement.
● The output carry is sent to flip-flop E, where it can be compared to two values to determine their relative magnitudes.
● When A and B are added, the add-overflow flip-flop AVF holds the overflow bit.
● Other micro operations that may be required while specifying the sequence of steps in the algorithm are provided by the A register.
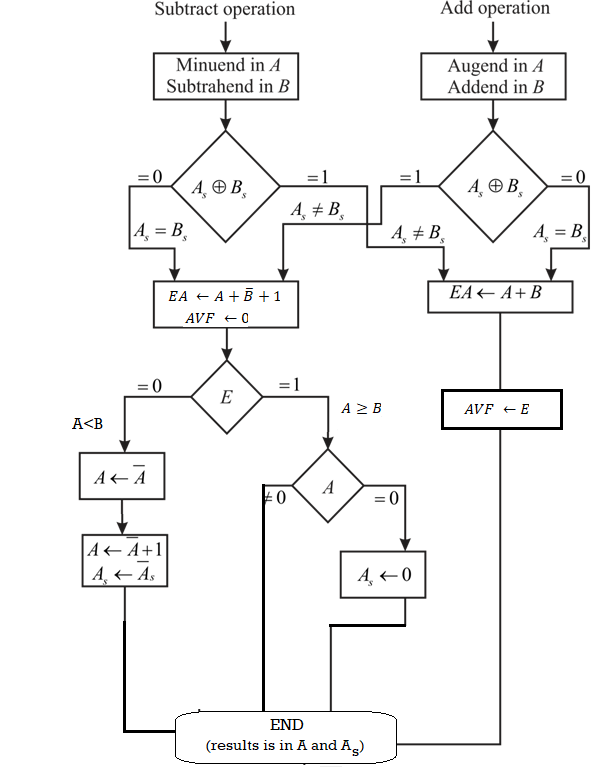
Fig 3: Flowchart for add and subtract operation
Q2) Explain multiplication algorithm?
A2) The booth algorithm is a multiplication algorithm that allows us to multiply the two signed binary integers in 2's complement, respectively. It is also used to speed up the performance of the multiplication process. It is very efficient too. It works on the string bits 0's in the multiplier that requires no additional bit only shift the right-most string bits and a string of 1's in a multiplier bit weight 2k to weight 2m that can be considered as 2k+ 1 - 2m.
Following is the pictorial representation of the Booth's Algorithm:
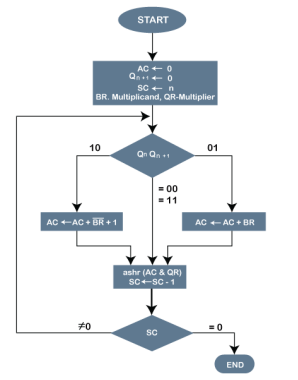
Fig 4- Pictorial representation of the Booth's Algorithm
In the above flowchart, initially, AC and Qn + 1 bits are set to 0, and the SC is a sequence counter that represents the total bits set n, which is equal to the number of bits in the multiplier. There are BR that represent the multiplicand bits, and QR represents the multiplier bits. After that, we encountered two bits of the multiplier as Qn and Qn + 1, where Qn represents the last bit of QR, and Qn + 1 represents the incremented bit of Qn by 1.
Suppose two bits of the multiplier is equal to 10; it means that we have to subtract the multiplier from the partial product in the accumulator AC and then perform the arithmetic shift operation (ashr). If the two of the multipliers equal to 01, it means we need to perform the addition of the multiplicand to the partial product in accumulator AC and then perform the arithmetic shift operation (ashr), including Qn + 1. The arithmetic shift operation is used in Booth's algorithm to shift AC and QR bits to the right by one and remains the sign bit in AC unchanged. And the sequence counter is continuously decremented till the computational loop is repeated, equal to the number of bits (n).
Working on the Booth Algorithm
- Set the Multiplicand and Multiplier binary bits as M and Q, respectively.
- Initially, we set the AC and Qn + 1 registers value to 0.
- SC represents the number of Multiplier bits (Q), and it is a sequence counter that is continuously decremented till equal to the number of bits (n) or reached to 0.
- A Qn represents the last bit of the Q, and the Qn+1 shows the incremented bit of Qn by 1.
- On each cycle of the booth algorithm, Qn and Qn + 1 bits will be checked on the following parameters as follows:
- When two bits Qn and Qn + 1 are 00 or 11, we simply perform the arithmetic shift right operation (ashr) to the partial product AC. And the bits of Qn and Qn + 1 is incremented by 1 bit.
- If the bits of Qn and Qn + 1 is shows to 01, the multiplicand bits (M) will be added to the AC (Accumulator register). After that, we perform the right shift operation to the AC and QR bits by 1.
- If the bits of Qn and Qn + 1 is shows to 10, the multiplicand bits (M) will be subtracted from the AC (Accumulator register). After that, we perform the right shift operation to the AC and QR bits by 1.
- The operation continuously works till we reached n - 1 bit in the booth algorithm.
- Results of the Multiplication binary bits will be stored in the AC and QR registers.
Q3) Write the different methods used in booth algorithm?
A3) There are two methods used in Booth's Algorithm:
1. RSC (Right Shift Circular)
It shifts the right-most bit of the binary number, and then it is added to the beginning of the binary bits.
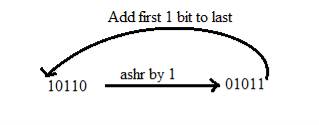
2. RSA (Right Shift Arithmetic)
It adds the two binary bits and then shift the result to the right by 1-bit position.
Example: 0100 + 0110 => 1010, after adding the binary number shift each bit by 1 to the right and put the first bit of resultant to the beginning of the new bit.
Example: Multiply the two numbers 7 and 3 by using the Booth's multiplication algorithm.
Ans. Here we have two numbers, 7 and 3. First of all, we need to convert 7 and 3 into binary numbers like 7 = (0111) and 3 = (0011). Now set 7 (in binary 0111) as multiplicand (M) and 3 (in binary 0011) as a multiplier (Q). And SC (Sequence Count) represents the number of bits, and here we have 4 bits, so set the SC = 4. Also, it shows the number of iteration cycles of the booth's algorithms and then cycles run SC = SC - 1 time.
Qn | Qn + 1 | M = (0111) M' + 1 = (1001) & Operation | AC | Q | Qn + 1 | SC |
1 | 0 | Initial | 0000 | 0011 | 0 | 4 |
|
| Subtract (M' + 1) | 1001 |
|
|
|
|
|
| 1001 |
|
|
|
|
| Perform Arithmetic Right Shift operations (ashr) | 1100 | 1001 | 1 | 3 |
1 | 1 | Perform Arithmetic Right Shift operations (ashr) | 1110 | 0100 | 1 | 2 |
0 | 1 | Addition (A + M) | 0111 |
|
|
|
|
|
| 0101 | 0100 |
|
|
|
| Perform Arithmetic right shift operation | 0010 | 1010 | 0 | 1 |
0 | 0 | Perform Arithmetic right shift operation | 0001 | 0101 | 0 | 0 |
The numerical example of the Booth's Multiplication Algorithm is 7 x 3 = 21 and the binary representation of 21 is 10101. Here, we get the resultant in binary 00010101. Now we convert it into decimal, as (000010101)10 = 2*4 + 2*3 + 2*2 + 2*1 + 2*0 => 21.
Example: Multiply the two numbers 23 and -9 by using the Booth's multiplication algorithm.
Here, M = 23 = (010111) and Q = -9 = (110111)
Qn Qn + 1 | M = 0 1 0 1 1 1 M' + 1 = 1 0 1 0 0 1 | AC | Q | Qn + 1 SC |
| Initially | 000000 | 110111 | 0 6 |
1 0 | Subtract M | 101001 |
|
|
|
| 101001 |
|
|
| Perform Arithmetic right shift operation | 110100 | 111011 | 1 5 |
1 1 | Perform Arithmetic right shift operation | 111010 | 011101 | 1 4 |
1 1 | Perform Arithmetic right shift operation | 111101 | 001110 | 1 3 |
0 1 | Addition (A + M) | 010111 |
|
|
|
| 010100 |
|
|
| Perform Arithmetic right shift operation | 001010 | 000111 | 0 2 |
1 0 | Subtract M | 101001 |
|
|
|
| 110011 |
|
|
| Perform Arithmetic right shift operation | 111001 | 100011 | 1 1 |
1 1 | Perform Arithmetic right shift operation | 111100 | 110001 | 1 0 |
Qn + 1 = 1, it means the output is negative.
Hence, 23 * -9 = 2's complement of 111100110001 => (00001100111)
Q4) Explain division algorithm?
A4) In division algorithm dividend will be greater than or equal to zero, overflow condition occurs when flipflop is set we call it divide overflow flipflop and label it DVF
To avoid DVF floating point data can be used

Hardware Algorithm
● Dividend is in A and Q and the divisor in B, the sign of the result is transferred into Qs to be part of quotient
● Overflow condition is tested by subtracting divisor in B from half of the bits of the dividend stored in A
● If A>B the divide overflow flip flop DVF is set and the operation is terminated
● As shown in flowchart the quotient magnitude is formed in register Q and the remainder is found in the register A
● Quotient sign is in QS and the sign of the remainder in AS is same as the original sign of the dividend
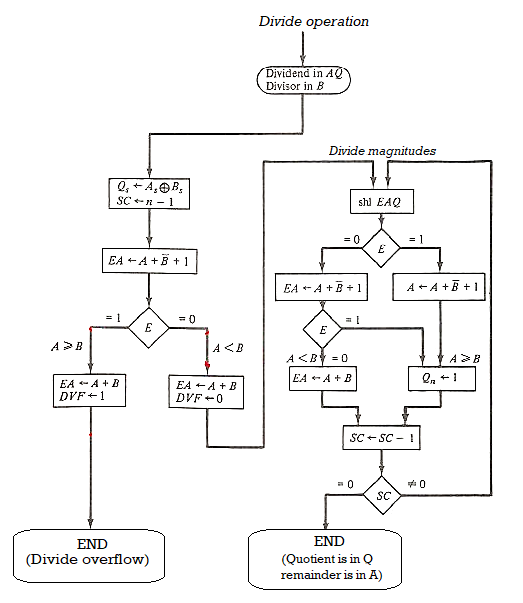
Figure 5 - Hardware Algorithm for Division
INSTRUCTION SET:
● Instruction set or Instruction Set Architecture (ISA) is the part of the processor that is visible to the programmer or compiler writer.
● The ISA serves as the boundary between software and hardware.
● The ISA defines the types of instructions to be supported by the processor.
Q5) Classify the instruction?
A5) Instructions are classified into 3 types:
Arithmetic/Logic Instructions: These Instructions perform various Arithmetic & logical operations on one or more operands
Data Transfer Instructions: These Instructions are responsible for the transfer of instruction from memory to the processor registers and vice versa
Branch and jump Instructions: These Instructions are responsible for breaking the sequential flow of instruction and jumping to instructions at various other locations for the implementation of functions and conditional statements
Q6) Explain floating arithmetic?
A6) The objectives of this module are to discuss the need for floating-point numbers, the standard representation used for floating-point numbers, and discuss how the various floating-point arithmetic operations of addition, subtraction, multiplication, and division are carried out.
Floating-point numbers and operations Representation
When you have to represent very small or very large numbers, a fixed point representation will not do. The accuracy will be lost. Therefore, you will have to look at floating-point representations, where the binary point is assumed to be floating. When you consider a decimal number 12. 34 * 107, this can also be treated as 0. 1234 * 109, where 0. 1234 is the fixed-point mantissa. The other part represents the exponent value and indicates that the actual position of the binary point is 9 positions to the right (left) of the indicated binary point in the fraction. Since the binary point can be moved to any position and the exponent value adjusted appropriately, it is called a floating-point representation. By convention, you generally go in for a normalized representation, wherein the floating-point is placed to the right of the first nonzero (significant) digit. The base need not be specified explicitly and the sign, the significant digits, and the signed exponent constitute the representation.
The IEEE (Institute of Electrical and Electronics Engineers) has produced a standard for floating-point arithmetic. This standard specifies how single-precision (32 bit) and double-precision (64 bit) floating-point numbers are to be represented, as well as how arithmetic should be carried out on them. The IEEE single-precision floating-point standard representation requires a 32-bit word, which may be represented as numbered from 0 to 31, left to right. The first bit is the sign bit, S, the next eight bits are the exponent bits, ‘E’, and the final 23 bits are the fraction ‘F’. Instead of the signed exponent E, the value stored is an unsigned integer E’ = E + 127, called the excess-127 format. Therefore, E’ is in the range 0 £ E’ £ 255.
S E’E’E’E’E’E’E’E’ FFFFFFFFFFFFFFFFFFFFFFF
0 1 8 9 31
The value V represented by the word may be determined as follows:
● If E’ = 255 and F is nonzero, then V = NaN (“Not a number”)
● If E’ = 255 and F is zero and S is 1, then V = -Infinity
● If E’ = 255 and F is zero and S is 0, then V = Infinity
● If 0 < E< 255 then V =(-1)**S * 2 ** (E-127) * (1. F) where “1. F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.
● If E’ = 0 and F is nonzero, then V = (-1)**S * 2 ** (-126) * (0. F). These are “unnormalized” values.
● If E’= 0 and F is zero and S is 1, then V = -0
● If E’ = 0 and F is zero and S is 0, then V = 0
For example,
0 00000000 00000000000000000000000 = 0
1 00000000 00000000000000000000000 = -0
0 11111111 00000000000000000000000 = Infinity
1 11111111 00000000000000000000000 = -Infinity
0 11111111 00000100000000000000000 = NaN
1 11111111 00100010001001010101010 = NaN
0 10000000 00000000000000000000000 = +1 * 2**(128-127) * 1. 0 = 2
0 10000001 10100000000000000000000 = +1 * 2**(129-127) * 1. 101 = 6. 5
1 10000001 10100000000000000000000 = -1 * 2**(129-127) * 1. 101 = -6. 5
0 00000001 00000000000000000000000 = +1 * 2**(1-127) * 1. 0 = 2**(-126)
0 00000000 10000000000000000000000 = +1 * 2**(-126) * 0. 1 = 2**(-127)
0 00000000 00000000000000000000001 = +1 * 2**(-126) *
0. 00000000000000000000001 = 2**(-149) (Smallest positive value)
(unnormalized values)
Double Precision Numbers:
The IEEE double-precision floating point standard representation requires a 64-bit word, which may be represented as numbered from 0 to 63, left to right. The first bit is the sign bit, S, the next eleven bits are the excess-1023 exponent bits, E’, and the final 52 bits are the fraction ‘F’:
S E’E’E’E’E’E’E’E’E’E’E’
FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
0 1 11 12
63
The value V represented by the word may be determined as follows:
● If E’ = 2047 and F is nonzero, then V = NaN (“Not a number”)
● If E’= 2047 and F is zero and S is 1, then V = -Infinity
● If E’= 2047 and F is zero and S is 0, then V = Infinity
● If 0 < E’< 2047 then V = (-1)**S * 2 ** (E-1023) * (1. F) where “1. F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.
● If E’= 0 and F is nonzero, then V = (-1)**S * 2 ** (-1022) * (0. F) These are “unnormalized” values.
● If E’= 0 and F is zero and S is 1, then V = – 0
● If E’= 0 and F is zero and S is 0, then V = 0
Q7) What do you mean by signed number representation?
A7) Signed Number Representation
Variables such as integers can be represented in two ways, i. e. , signed and unsigned. Signed numbers use a sign flag or can distinguish between negative values and positive values. Whereas unsigned numbers stored only positive numbers but not negative numbers.
Number representation techniques like Binary, Octal, Decimal, and Hexadecimal number representation techniques can represent numbers in both signed and unsigned ways. Binary Number System is one type of Number Representation techniques. It is most popular and used in digital systems. The binary system is used for representing binary quantities which can be represented by any device that has only two operating states or possible conditions. For example, a switch has only two states: open or close.
In the Binary System, there are only two symbols or possible digit values, i. e., 0 and 1. Represented by any device that only has 2 operating states or possible conditions. Binary numbers are indicated by the addition of either an 0b prefix or a 2 suffix.
Representation of Binary Numbers:
Binary numbers can be represented in the signed and unsigned way. Unsigned binary numbers do not have a sign bit, whereas signed binary numbers use a signed bit as well or these can be distinguishable between positive and negative numbers. A signed binary is a specific data type of a signed variable.
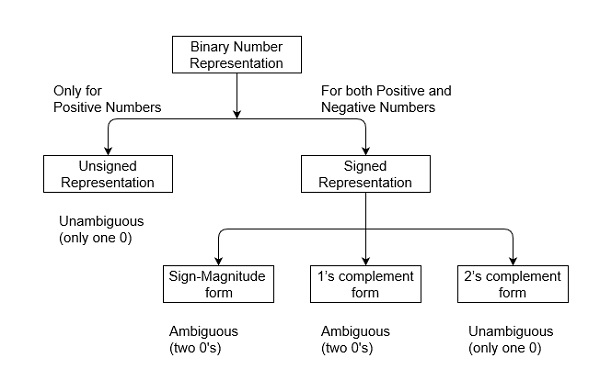
Fig 6: Binary number representation