Unit – 3

2D Transformation

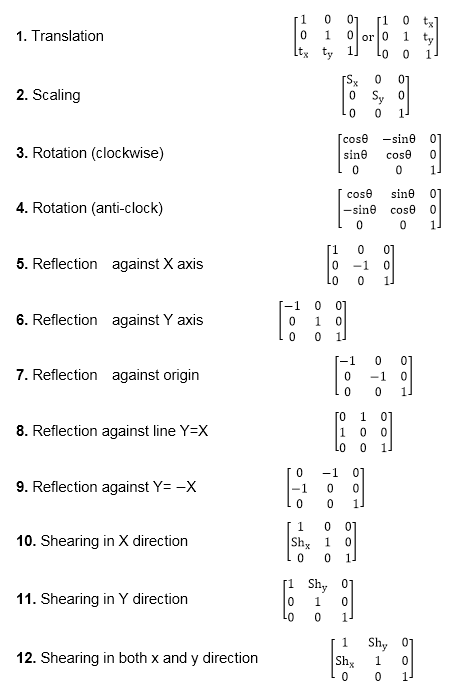
Q1) Write short notes on 2D transformation?

A1) The transformation means the translating some graphics into something else.

It has some rules to apply on the changing graphics.

Some transformations are such as translation, scaling up or down, shearing, rotating etc.

The transformation that applies on the 2D plane this is called as 2D transformation.

It is important in computer graphics to reposition the graphic on the screen and change their size or orientation.

The term "transformation" refers to the process of applying rules to change one set of visuals into another. Different forms of transformations are possible, such as translation, scaling up or down, rotation, shearing, and so on. The term "2D transformation" refers to a transformation that occurs on a two-dimensional plane.

In computer graphics, transformations are used to rearrange graphics on the screen and modify their size or orientation.

Q2) What is translation?

A2) The translation process is used to move an abject to the different position on the screen.

The translation done by adding translation coordinates (tx,ty) to the original coordinates.

The figure shows the translation process.

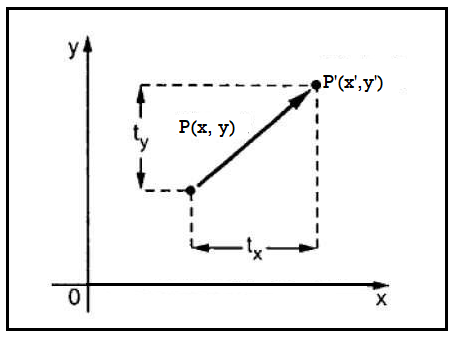
Fig 1: Translation

In the figure,

X’=X+tx

Y’=Y+ty

The pair (tx,ty) is called the translation vector or shift vector.

The equation can be represent by column vector.

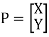
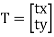
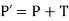
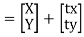
Q3) Define scaling?

A3) The scaling transformation is done for changing the size of abject.

The dimension of the abject can be compress or expand by using scaling.

The scaling can be achieved by multiplying the original coordinates with the scaling factor to get the desired result.

The scaling factors be Sx and Sy with respt to x and y coordinates.

If the value assigned to the scaling factor S is less than 1 then the size of the abject will compressed.

If the value assigned to the scaling factor S is greater than 1 then the size of the abject will increased.

Following figure shows the scaling process.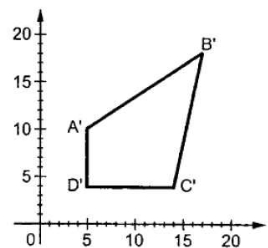

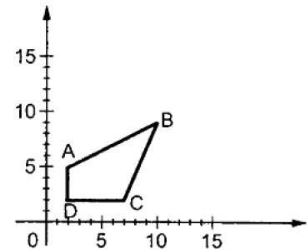
Fig 2: Scaling

Let assume that the original coordinates are X and Y and the scaling factors are (Sx,Sy).

The mathematics representation of the scaling represented as shown below:

X’=X * Sx

And Y’=Y * Sy

The above equation can be represented in matrix form as shown below:

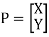
And

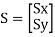
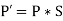
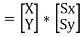
Q4) What do you mean by rotation?

A4) The rotation is used for rotating the object at particular angle Ꙫ from its origin.

The following figure shows the point P that is located at angle ф from the horizontal X coordinate with distance r from the origin.

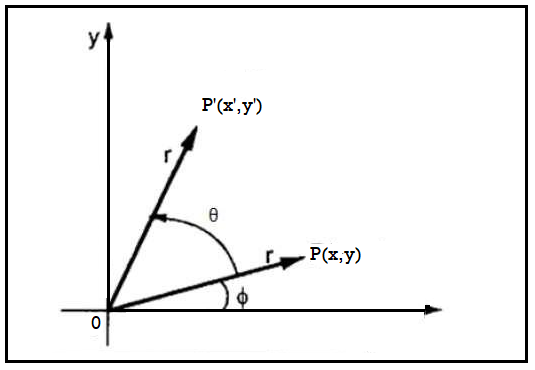
Fig 3: Rotation

The rotation is achieved by using the following rotation equation:

X’=X * cos  - Y * sin 

Y’ =X * sin   + Y * cos 

In matrix for, the clockwise rotation represented as shown below:

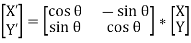
In matrix for, the anti-clockwise rotation represented as shown below:

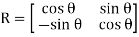
The homogeneous coordinates will be represented as:

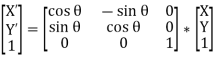
Q5) Write notes on homogeneous coordinates?

A5) Homogeneous coordinates

A point, a straight line, or a full image on the screen can be rotated around a point other than the origin by first moving the image until the point of rotation occupies the origin, then rotating the image, and then moving the image back to its original location.

A translation is the process of shifting a picture from one location to another in a straight line. A translation can be done by adding or subtracting the amount that the picture has to be displaced from each location.

The use of a simple matrix application to translate a point by changing its coordinates cannot be combined with additional transformations. If we want to rotate an image around a point other than the origin by translation, rotation, and translation, we'll need this combination.

Homogeneous coordinates are used to merge these three transformations into a single transformation. Two-dimensional coordinate positions (x, y) are represented by triple-coordinates in a homogeneous coordinate system.

In most design and construction applications, homogeneous coordinates are used. To put the picture into the right place, we execute translations, rotations, and scaling here.

The homogeneous coordinates are used to perform any transformation such as the translation followed by rotation and the scaling.

The translation follows the sequential process as-

●      Translate the coordinates

●      Rotate the translated coordinates

●      Scale the rotated coordinates to complete the transformation

The process can be shortened by using the matrix of 3*3 instead of using matrix 2*2. This matrix is called a transformation matrix.

To convert 2*2 matrix in 3*3 we have to add just coordinate w.

In this way, the representation of points by 3 numbers instead of 2 numbers, is known as the homogeneous coordinates.

We can represent all the transformation by using homogeneous coordinates in matrix multiplication.

Any Cartesian point can be converted to homogeneous coordinates by P’ (Xh, Yh, h)

Q6) How to transform coordinate systems?

A6) A translation is the process of shifting a picture from one location to another in a straight line. A translation can be done by adding or subtracting the amount that the picture has to be displaced from each location.

The use of a simple matrix application to translate a point by changing its coordinates cannot be combined with additional transformations. If we want to rotate an image around a point other than the origin by translation, rotation, and translation, we'll need this combination.

Homogeneous coordinates are used to merge these three transformations into a single transformation. Two-dimensional coordinate positions (x, y) are represented by triple-coordinates in a homogeneous coordinate system.

In most design and construction applications, homogeneous coordinates are used. To put the picture into the right place, we execute translations, rotations, and scaling here.

Example

An example of how to represent coordinates in a homogeneous coordinate system is as follows: We can set the homogeneous parameter h to any non-zero value for two-dimensional geometric transformation. Take it as one for the sake of convenience. The homogeneous coordinates are then used to represent each two-dimensional point (x, y, 1).

The matrix for two-dimensional transformation in homogeneous coordinate is as follows:

Q7) Explain reflection shear?

A7) Reflection Transformation

All the points are reflected or flipped on a line called axis reflection or line of reflection.

The reflection can be referred to as an axis of symmetry or mirror line.

The reflected diagram is the same as the original diagram is known as isometric transformation.

The reflected diagram is facing in opposite direction.

Following figure shows the reflection transformation.

Fig. 5

Shearing Transformation

The shear transformation is used for slanting the shape of the object.

Shearing is also known as skewing.

There are two shear transformations X-shear and Y-shear.

The X-shear shifts the X coordinates and the Y-shear shifts the Y coordinates.

In both cases only one coordinate changes and the other preserves.

X-shear:

It preserves the Y coordinate and changes made with the X coordinate.

Hence only vertical lines of the object get tilt on the right or left side as shown in the below figure:

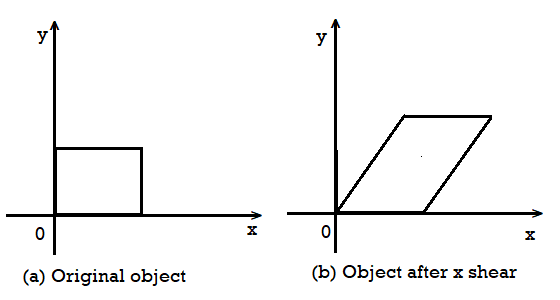
Fig 6

The transformation matrix for X- shear:

Y’=Y + Shy * X   and X’=X

Y-shear:

It preserves the X coordinates and makes changes with the Y coordinates.

The horizontal line of the object slopes toward up or down as shown in the below figure:

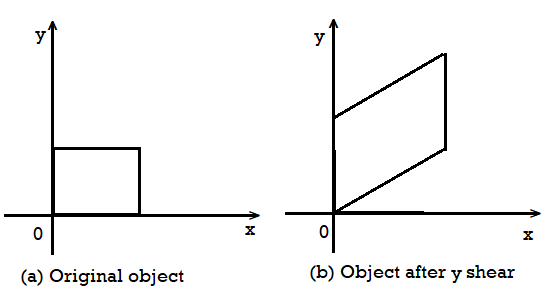
Fig 7

The transformation matrix for X- shear:

X’=X + Shx * Y   and Y’=Y

Q8) What is transformation?

A8) A point, a straight line, or a full image on the screen can be rotated around a point other than the origin by first moving the image until the point of rotation occupies the origin, then rotating the image, and then moving the image back to its original location.

Computer graphics allow you to observe objects from many perspectives. The architect can look at a building from several perspectives, for example.

●      Front Evaluation

●      Side elevation

●      Top plan

Charts and topographical maps can be resized by a cartographer. As a result, if visual images are encoded as numbers, the numbers can be saved in memory. Transformation is a mathematical operation that modifies certain numbers.

The goal of using computers for drawing is to allow users to observe objects from various angles, extending or lowering the scale or shape of the object, which is known as transformation.

The following are two crucial characteristics of transformation:

●      Each change is treated as a separate entity. A distinct name or symbol might be used to identify it.

●      After linking two transformations, a single transformation can be obtained, for example, A is a translation transformation. Scaling is done via the B transformation. C=AB is the result of combining the two. As a result of the concatenation property, C is obtained.

For explaining object transformation, there are two complimentary ways of view.

●      Geometric Transformation - The object is transformed in relation to the background or coordinate system. Geometric transformations applied to each point of the object define the mathematical description of this viewpoint.

●      Coordinate Transformation:  While the coordinate system is altered relative to the object, the object is held immobile. The use of coordinate transformations is used to achieve this effect.

Here's an example of how these two points of view can be distinguished:

The motion of a car against a beautiful backdrop. We can do so by simulating

●      Moving the car while keeping the background in place- (Geometric Transformation).

●      We can keep the car in working order while changing the scenery in the background- (Coordinate Transformation).

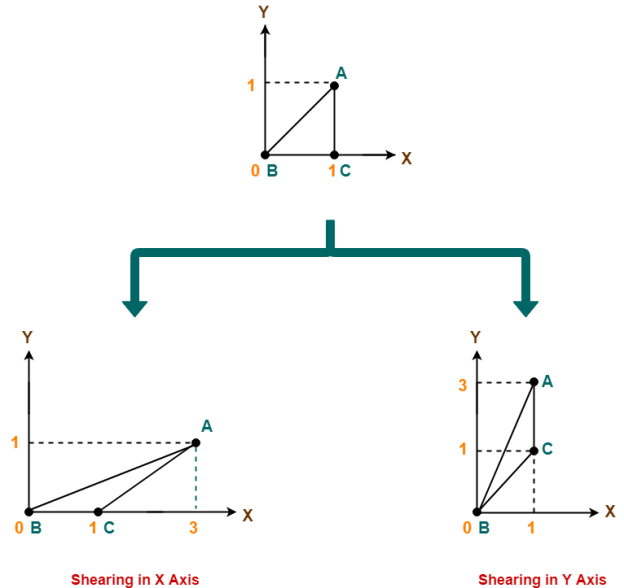
Q9) Given a triangle with points (1, 1), (0, 0) and (1, 0). Apply shear parameter 2 on X axis and 2 on Y axis and find out the new coordinates of the object?

A9) Given-

Shearing in X Axis-

For Coordinates A(1, 1)

Let the new coordinates of corner A after shearing = (Xnew, Ynew).

Applying the shearing equations, we have-

Thus, New coordinates of corner A after shearing = (3, 1).

For Coordinates B(0, 0)

Let the new coordinates of corner B after shearing = (Xnew, Ynew).

Applying the shearing equations, we have-

Thus, New coordinates of corner B after shearing = (0, 0).

For Coordinates C(1, 0)

Let the new coordinates of corner C after shearing = (Xnew, Ynew).

Applying the shearing equations, we have-

Thus, New coordinates of corner C after shearing = (1, 0).

Thus, New coordinates of the triangle after shearing in X axis = A (3, 1), B(0, 0), C(1, 0).

Shearing in Y Axis-

For Coordinates A(1, 1)

Let the new coordinates of corner A after shearing = (Xnew, Ynew).

Applying the shearing equations, we have-

Thus, New coordinates of corner A after shearing = (1, 3).

For Coordinates B(0, 0)

Let the new coordinates of corner B after shearing = (Xnew, Ynew).

Applying the shearing equations, we have-

Thus, New coordinates of corner B after shearing = (0, 0).

For Coordinates C(1, 0)

Let the new coordinates of corner C after shearing = (Xnew, Ynew).

Applying the shearing equations, we have-

Thus, New coordinates of corner C after shearing = (1, 2).

Thus, New coordinates of the triangle after shearing in Y axis = A (1, 3), B(0, 0), C(1, 2).

Q10) Given a circle C with radius 10 and center coordinates (1, 4). Apply the translation with distance 5 towards X axis and 1 towards Y axis. Obtain the new coordinates of C without changing its radius?

A10) Given-

Old center coordinates of C = (Xold, Yold) = (1, 4)

Translation vector = (Tx, Ty) = (5, 1)

Let the new center coordinates of C = (Xnew, Ynew).

Applying the translation equations, we have-

Xnew = Xold + Tx = 1 + 5 = 6

Ynew = Yold + Ty = 4 + 1 = 5

Thus, New center coordinates of C = (6, 5).

Alternatively,

In matrix form, the new center coordinates of C after translation may be obtained as-

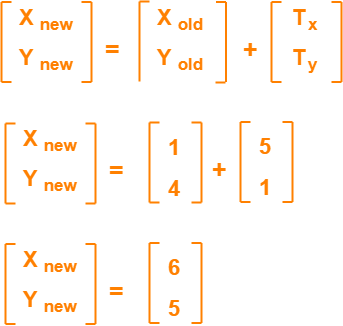
Thus, New center coordinates of C = (6, 5).

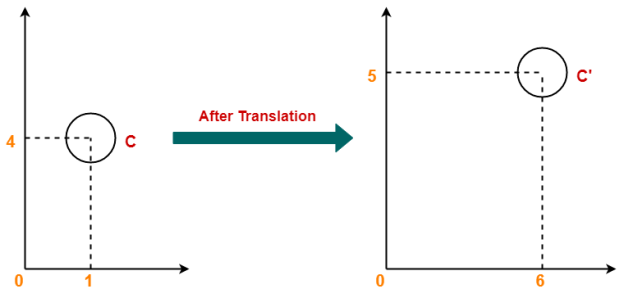
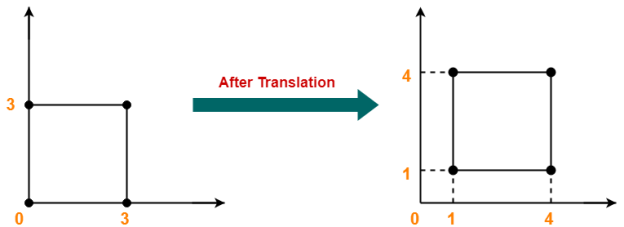
Q11) Given a square with coordinate points A(0, 3), B(3, 3), C(3, 0), D(0, 0). Apply the translation with distance 1 towards X axis and 1 towards Y axis. Obtain the new coordinates of the square.

A11) Given-

Old coordinates of the square = A (0, 3), B(3, 3), C(3, 0), D(0, 0)

Translation vector = (Tx, Ty) = (1, 1)

For Coordinates A(0, 3)

Let the new coordinates of corner A = (Xnew, Ynew).

Applying the translation equations, we have-

Xnew = Xold + Tx = 0 + 1 = 1

Ynew = Yold + Ty = 3 + 1 = 4

Thus, New coordinates of corner A = (1, 4).

For Coordinates B(3, 3)

Let the new coordinates of corner B = (Xnew, Ynew).

Applying the translation equations, we have-

Xnew = Xold + Tx = 3 + 1 = 4

Ynew = Yold + Ty = 3 + 1 = 4

Thus, New coordinates of corner B = (4, 4).

For Coordinates C(3, 0)

Let the new coordinates of corner C = (Xnew, Ynew).

Applying the translation equations, we have-

Xnew = Xold + Tx = 3 + 1 = 4

Ynew = Yold + Ty = 0 + 1 = 1

Thus, New coordinates of corner C = (4, 1).

For Coordinates D(0, 0)

Let the new coordinates of corner D = (Xnew, Ynew).

Applying the translation equations, we have-

Xnew = Xold + Tx = 0 + 1 = 1

Ynew = Yold + Ty = 0 + 1 = 1

Thus, New coordinates of corner D = (1, 1).

Thus, New coordinates of the square = A (1, 4), B(4, 4), C(4, 1), D(1, 1).

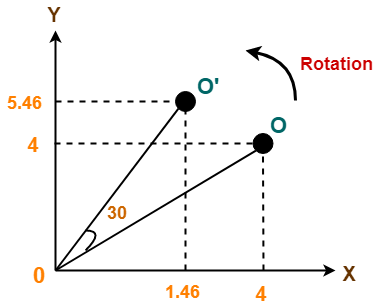
Q12) Given a line segment with starting point as (0, 0) and ending point as (4, 4). Apply 30 degree rotation anticlockwise direction on the line segment and find out the new coordinates of the line?

A12) We rotate a straight line by its end points with the same angle. Then, we re-draw a line between the new end points.

Given-

Old ending coordinates of the line = (Xold, Yold) = (4, 4)

Rotation angle = θ = 30º

Let new ending coordinates of the line after rotation = (Xnew, Ynew).

Applying the rotation equations, we have-

Xnew

= Xold x cosθ – Yold x sinθ

= 4 x cos30º – 4 x sin30º

= 4 x (√3 / 2) – 4 x (1 / 2)

= 2√3 – 2

= 2(√3 – 1)

= 2(1.73 – 1)

= 1.46

Ynew

= Xold x sinθ + Yold x cosθ

= 4 x sin30º + 4 x cos30º

= 4 x (1 / 2) + 4 x (√3 / 2)

= 2 + 2√3

= 2(1 + √3)

= 2(1 + 1.73)

= 5.46

Thus, New ending coordinates of the line after rotation = (1.46, 5.46).

Alternatively,

In matrix form, the new ending coordinates of the line after rotation may be obtained as-

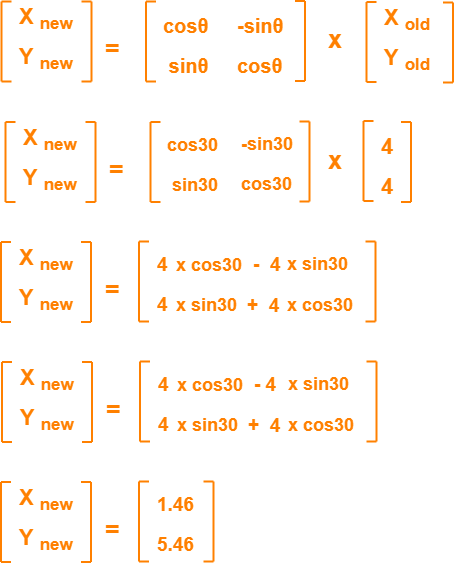
Thus, New ending coordinates of the line after rotation = (1.46, 5.46).

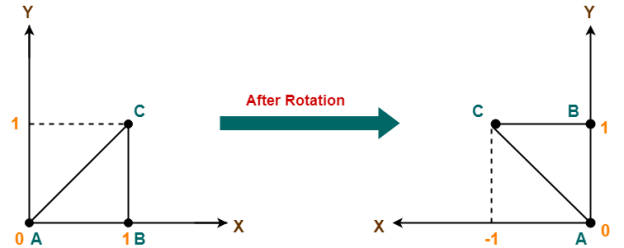
Q13) Given a triangle with corner coordinates (0, 0), (1, 0) and (1, 1). Rotate the triangle by 90 degree anticlockwise direction and find out the new coordinates?

A13) We rotate a polygon by rotating each vertex of it with the same rotation angle.

Given-

Old corner coordinates of the triangle = A (0, 0), B(1, 0), C(1, 1)

Rotation angle = θ = 90º

For Coordinates A(0, 0)

Let the new coordinates of corner A after rotation = (Xnew, Ynew).

Applying the rotation equations, we have-

Xnew

= Xold x cosθ – Yold x sinθ

= 0 x cos90º – 0 x sin90º

= 0

Ynew

= Xold x sinθ + Yold x cosθ

= 0 x sin90º + 0 x cos90º

= 0

Thus, New coordinates of corner A after rotation = (0, 0).

For Coordinates B(1, 0)

Let the new coordinates of corner B after rotation = (Xnew, Ynew).

Xnew

= Xold x cosθ – Yold x sinθ

= 1 x cos90º – 0 x sin90º

= 0

Ynew

= Xold x sinθ + Yold x cosθ

= 1 x sin90º + 0 x cos90º

= 1 + 0

= 1

Thus, New coordinates of corner B after rotation = (0, 1).

For Coordinates C(1, 1)

Let the new coordinates of corner C after rotation = (Xnew, Ynew).

Xnew

= Xold x cosθ – Yold x sinθ

= 1 x cos90º – 1 x sin90º

= 0 – 1

= -1

Ynew

= Xold x sinθ + Yold x cosθ

= 1 x sin90º + 1 x cos90º

= 1 + 0

= 1

Thus, New coordinates of corner C after rotation = (-1, 1).

Thus, New coordinates of the triangle after rotation = A (0, 0), B(0, 1), C(-1, 1).