Unit - 5
Complex Variable - Differentiation
Q1) Find-
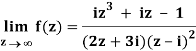
A1)
Here we have-
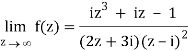
Divide numerator and denominator by z3, we get-
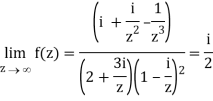
Q2) If f(z) is a complex function given below, then discuss dz/dz at z = 0
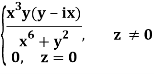
A2)
If z→0 along radius vector y = mx
= 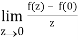
= 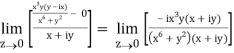
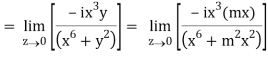

But along v = x3,
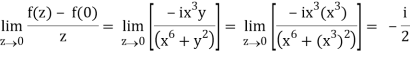
In different paths we get different value of df/dz that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Q3) Prove: The necessary condition for a function 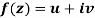 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
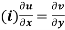 (ii)
(ii) 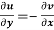
Provided, 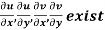
A3)
Let  be an analytic function in region R.
be an analytic function in region R.
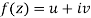
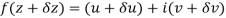
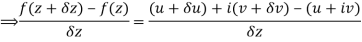
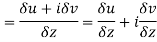
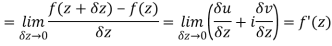
Along real axis


Then f’(z), becomes-
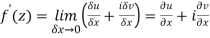 ………… (1)
………… (1)
Along imaginary axis

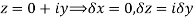
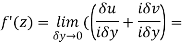
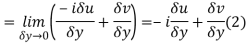
From equation (1) and (2)
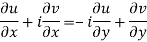
Equating real and imaginary parts
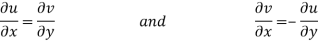
Therefore-
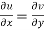 and
and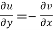
These are called Cauchy Riemann Equations.
Q4) What is Analytic function and write is necessary conditions?
A4)
A function 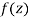 is said to be analytic at a point
is said to be analytic at a point 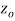 if f is differentiable not only at
if f is differentiable not only at 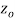 but every point of some neighborhood at
but every point of some neighborhood at  .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1.  …………. (1)
…………. (1)
2. 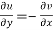 ……...…. (2)
……...…. (2)
Provided 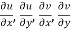 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1.  …………. (1)
…………. (1)
2. 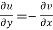 ……...…. (2)
……...…. (2)
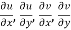 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Q5) State and prove sufficient condition for analytic functions
A5)
Statement – The sufficient condition for a function 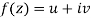 to be analytic at all points in a region R are
to be analytic at all points in a region R are
1. 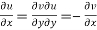
2. 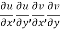 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having 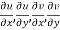 at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem

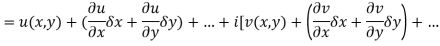

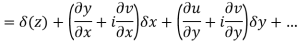
Ignoring the terms of second power and higher power

We know C-R equation
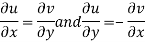
Replacing 
Respectively in (1) we get
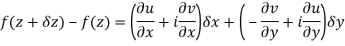
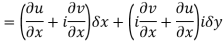
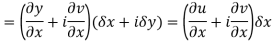
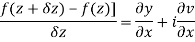
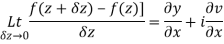
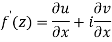
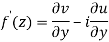
Q6) Show that 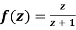 is analytic at
is analytic at 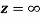
A6)
The function f(z) is analytic at  if the function
if the function  is analytic at z=0
is analytic at z=0
Since 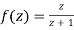
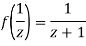
Now 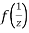 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 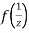 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 
Q7) If w = log z, then find 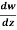 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A7)
Here we have 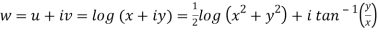
Therefore-
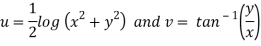
 and
and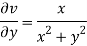
Again-

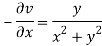
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0

Q8) Prove that the function  is an analytical function.
is an analytical function.
A8)
Let 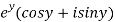 =u+iv
=u+iv
Let 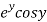 =u and
=u and 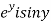 =v
=v

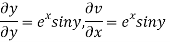
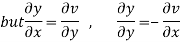
Hence C-R-Equation satisfied.
Q9) Prove that 
A9)
Given that
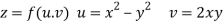
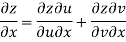
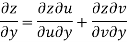
Since 

V=2xy

Now 
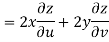

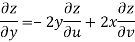
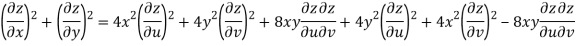
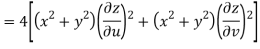
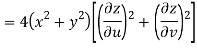
But 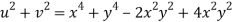
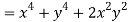
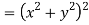
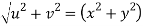
Hence 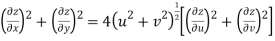
Q10) Show that polar form of C-R equations are-
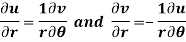
A10)
z = x + iy = 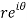
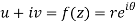
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-

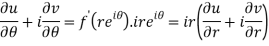
By equating real and imaginary parts, we get-
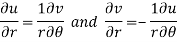
Q11) Prove Harmonic function theorem.
A11)
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
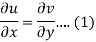
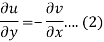
Differentiate (1) with respect to x, we get
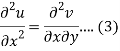
Differentiate (2) with respect to y, we get
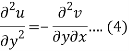
Add 3 and 4-
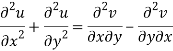

Similarly-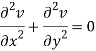
So that u and v are harmonic functions.
Q12) Prove that 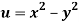 and
and  are harmonic functions of (x, y).
are harmonic functions of (x, y).
A12)
We have 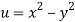
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
2v/x2 = 
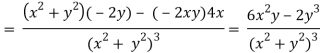

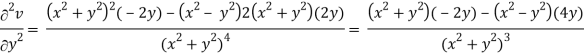
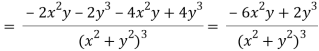
On adding the above results-
We get-

So that v(x, y) is also a harmonic function.
Q13) Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A13)
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
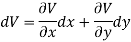
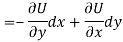
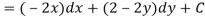

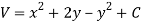
Hence the harmonic conjugate of U is 
Q14) Solve  where
where 
A14)
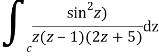
Where 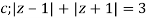
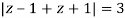
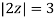
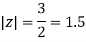
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1

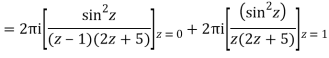

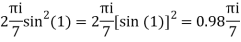
Q15) Solve 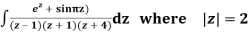
A15)

Poles are
|z-0|=2
Poles 1 and -1 inside the circle
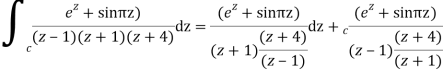
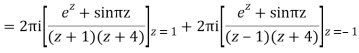
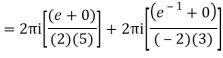
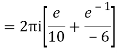
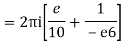
Q16) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 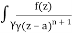
A16)
Given,
f(n)(a) = n!/2πi 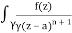
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 
= k!/2πi 
= (k+1)!/2πi 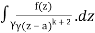
Q17) Evaluate 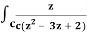 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A17)
It is given that-
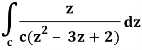
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
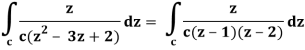

Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q18) Evaluate the integral given below by using Cauchy’s integral formula-

A18)
Here we have-

Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q19) Evaluate 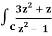 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
A19)
Here we have-
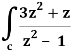
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
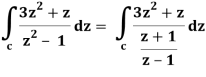 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q20) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A20)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q21) Find the singularity of the function-
f(z) = sin 1/z
A21)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q22) Show that when 0<|z|<4
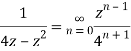
A22)
When |z|<4 we have
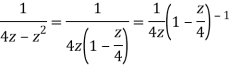
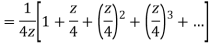
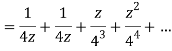
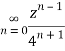
Q23) Find the residue of 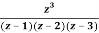 at z=1
at z=1
A23)
Let f(z)=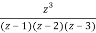
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=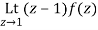
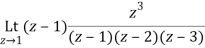
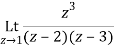
=1/2
Unit - 5
Complex Variable - Differentiation
Q1) Find-
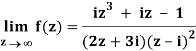
A1)
Here we have-

Divide numerator and denominator by z3, we get-
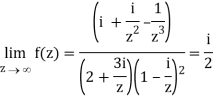
Q2) If f(z) is a complex function given below, then discuss dz/dz at z = 0
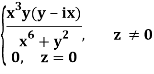
A2)
If z→0 along radius vector y = mx
= 
= 
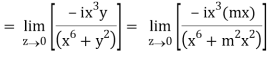
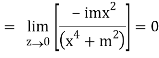
But along v = x3,
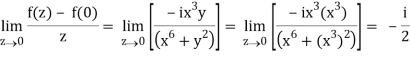
In different paths we get different value of df/dz that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Q3) Prove: The necessary condition for a function 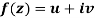 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
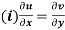 (ii)
(ii) 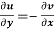
Provided, 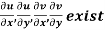
A3)
Let 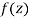 be an analytic function in region R.
be an analytic function in region R.

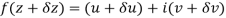
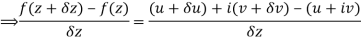
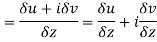
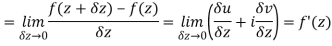
Along real axis
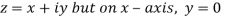
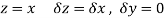
Then f’(z), becomes-
 ………… (1)
………… (1)
Along imaginary axis
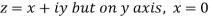
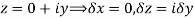
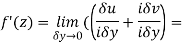

From equation (1) and (2)
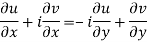
Equating real and imaginary parts
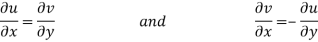
Therefore-
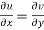 and
and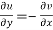
These are called Cauchy Riemann Equations.
Q4) What is Analytic function and write is necessary conditions?
A4)
A function  is said to be analytic at a point
is said to be analytic at a point 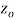 if f is differentiable not only at
if f is differentiable not only at  but every point of some neighborhood at
but every point of some neighborhood at  .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 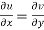 …………. (1)
…………. (1)
2. 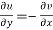 ……...…. (2)
……...…. (2)
Provided 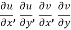 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 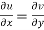 …………. (1)
…………. (1)
2. 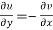 ……...…. (2)
……...…. (2)
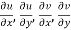 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Q5) State and prove sufficient condition for analytic functions
A5)
Statement – The sufficient condition for a function  to be analytic at all points in a region R are
to be analytic at all points in a region R are
1. 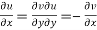
2.  are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having  at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
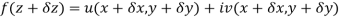
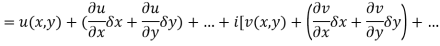
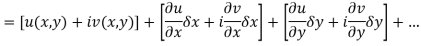

Ignoring the terms of second power and higher power

We know C-R equation

Replacing 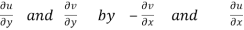
Respectively in (1) we get

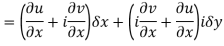



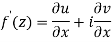

Q6) Show that  is analytic at
is analytic at 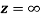
A6)
The function f(z) is analytic at 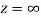 if the function
if the function 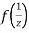 is analytic at z=0
is analytic at z=0
Since 
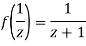
Now 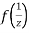 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 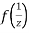 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 
Q7) If w = log z, then find 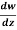 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A7)
Here we have 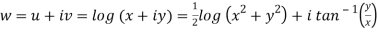
Therefore-
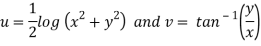
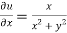 and
and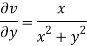
Again-
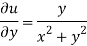
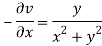
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0

Q8) Prove that the function  is an analytical function.
is an analytical function.
A8)
Let  =u+iv
=u+iv
Let 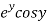 =u and
=u and  =v
=v
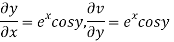

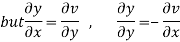
Hence C-R-Equation satisfied.
Q9) Prove that 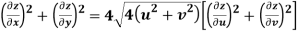
A9)
Given that
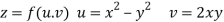
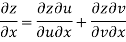
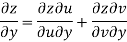
Since 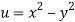

V=2xy

Now 
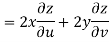
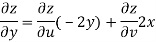
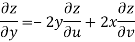
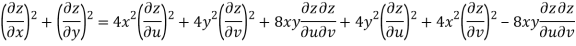
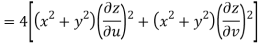
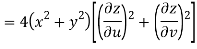
But 
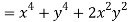
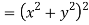
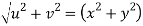
Hence 
Q10) Show that polar form of C-R equations are-
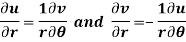
A10)
z = x + iy = 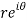
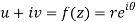
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
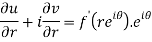
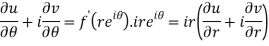
By equating real and imaginary parts, we get-

Q11) Prove Harmonic function theorem.
A11)
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
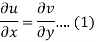
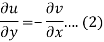
Differentiate (1) with respect to x, we get

Differentiate (2) with respect to y, we get
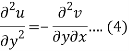
Add 3 and 4-
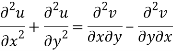
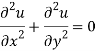
Similarly-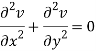
So that u and v are harmonic functions.
Q12) Prove that  and
and  are harmonic functions of (x, y).
are harmonic functions of (x, y).
A12)
We have 
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
2v/x2 = 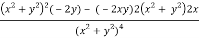
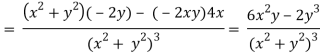
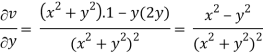
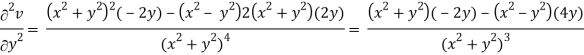

On adding the above results-
We get-

So that v(x, y) is also a harmonic function.
Q13) Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A13)
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
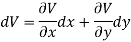

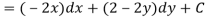

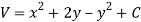
Hence the harmonic conjugate of U is 
Q14) Solve 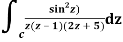 where
where 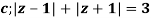
A14)
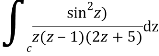
Where 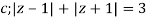
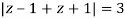
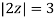

Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1


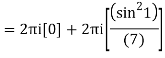

Q15) Solve 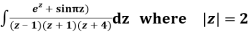
A15)
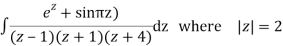
Poles are
|z-0|=2
Poles 1 and -1 inside the circle

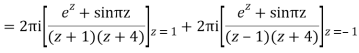

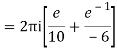
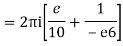
Q16) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 
A16)
Given,
f(n)(a) = n!/2πi 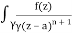
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 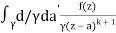
= k!/2πi 
= (k+1)!/2πi 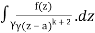
Q17) Evaluate 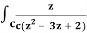 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A17)
It is given that-
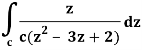
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
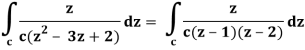
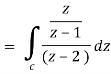
Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q18) Evaluate the integral given below by using Cauchy’s integral formula-

A18)
Here we have-
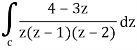
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
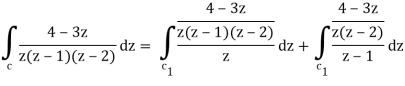 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q19) Evaluate 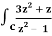 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
A19)
Here we have-
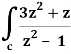
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q20) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A20)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q21) Find the singularity of the function-
f(z) = sin 1/z
A21)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q22) Show that when 0<|z|<4
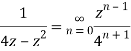
A22)
When |z|<4 we have
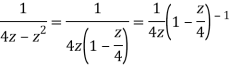
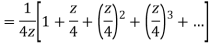
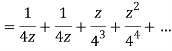
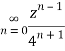
Q23) Find the residue of 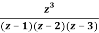 at z=1
at z=1
A23)
Let f(z)=
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=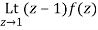
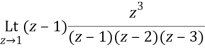
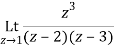
=1/2
Unit - 5
Complex Variable - Differentiation
Q1) Find-
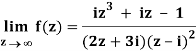
A1)
Here we have-

Divide numerator and denominator by z3, we get-

Q2) If f(z) is a complex function given below, then discuss dz/dz at z = 0
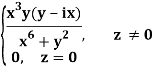
A2)
If z→0 along radius vector y = mx
= 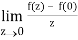
= 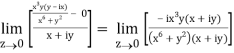
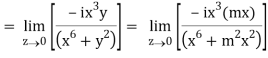
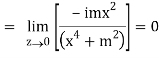
But along v = x3,
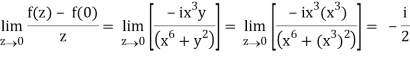
In different paths we get different value of df/dz that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Q3) Prove: The necessary condition for a function 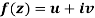 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
 (ii)
(ii) 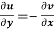
Provided, 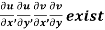
A3)
Let 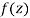 be an analytic function in region R.
be an analytic function in region R.
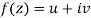
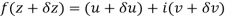
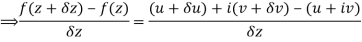
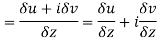

Along real axis
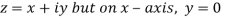
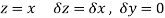
Then f’(z), becomes-
 ………… (1)
………… (1)
Along imaginary axis
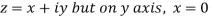

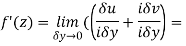
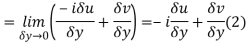
From equation (1) and (2)
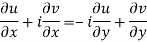
Equating real and imaginary parts

Therefore-
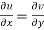 and
and
These are called Cauchy Riemann Equations.
Q4) What is Analytic function and write is necessary conditions?
A4)
A function 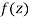 is said to be analytic at a point
is said to be analytic at a point 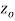 if f is differentiable not only at
if f is differentiable not only at 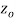 but every point of some neighborhood at
but every point of some neighborhood at 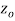 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 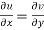 …………. (1)
…………. (1)
2. 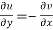 ……...…. (2)
……...…. (2)
Provided 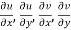 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 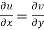 …………. (1)
…………. (1)
2. 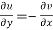 ……...…. (2)
……...…. (2)
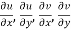 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Q5) State and prove sufficient condition for analytic functions
A5)
Statement – The sufficient condition for a function 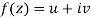 to be analytic at all points in a region R are
to be analytic at all points in a region R are
1. 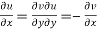
2. 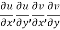 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having 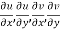 at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
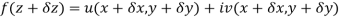

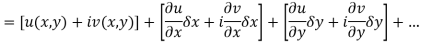
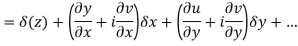
Ignoring the terms of second power and higher power

We know C-R equation
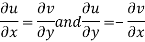
Replacing 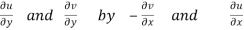
Respectively in (1) we get
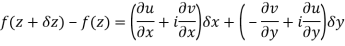

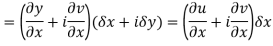
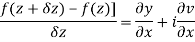



Q6) Show that  is analytic at
is analytic at 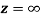
A6)
The function f(z) is analytic at 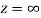 if the function
if the function  is analytic at z=0
is analytic at z=0
Since 
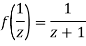
Now  is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 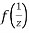 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 
Q7) If w = log z, then find 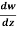 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A7)
Here we have 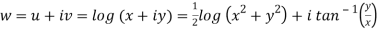
Therefore-
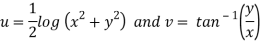
 and
and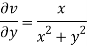
Again-
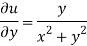

Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0

Q8) Prove that the function 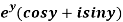 is an analytical function.
is an analytical function.
A8)
Let  =u+iv
=u+iv
Let 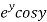 =u and
=u and 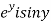 =v
=v
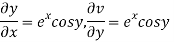
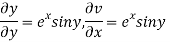
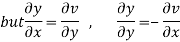
Hence C-R-Equation satisfied.
Q9) Prove that 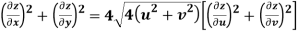
A9)
Given that
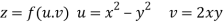
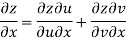
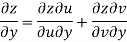
Since 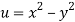

V=2xy

Now 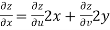
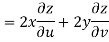
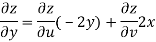

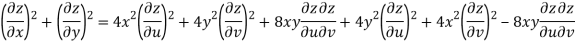

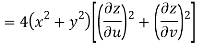
But 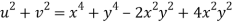


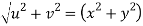
Hence 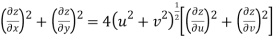
Q10) Show that polar form of C-R equations are-
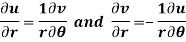
A10)
z = x + iy = 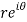
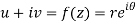
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
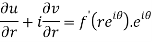

By equating real and imaginary parts, we get-
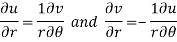
Q11) Prove Harmonic function theorem.
A11)
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
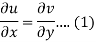
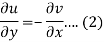
Differentiate (1) with respect to x, we get
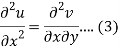
Differentiate (2) with respect to y, we get
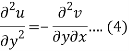
Add 3 and 4-
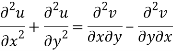

Similarly-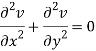
So that u and v are harmonic functions.
Q12) Prove that 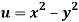 and
and  are harmonic functions of (x, y).
are harmonic functions of (x, y).
A12)
We have 
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
2v/x2 = 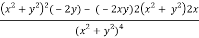
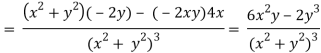

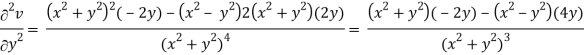
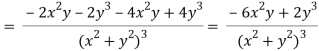
On adding the above results-
We get-
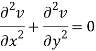
So that v(x, y) is also a harmonic function.
Q13) Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A13)
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
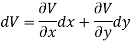
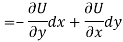
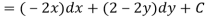
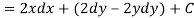

Hence the harmonic conjugate of U is 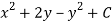
Q14) Solve 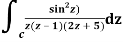 where
where 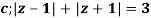
A14)
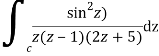
Where 
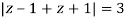

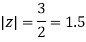
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
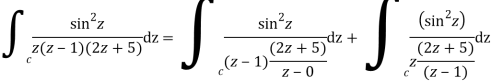
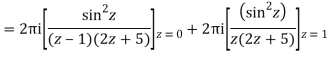

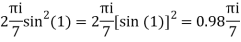
Q15) Solve 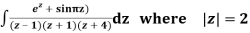
A15)
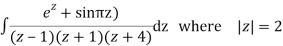
Poles are
|z-0|=2
Poles 1 and -1 inside the circle
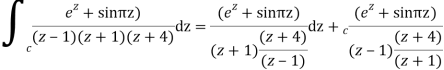
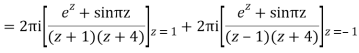
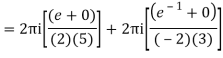
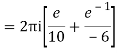

Q16) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 
A16)
Given,
f(n)(a) = n!/2πi 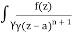
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 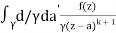
= k!/2πi 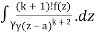
= (k+1)!/2πi 
Q17) Evaluate  dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A17)
It is given that-
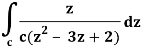
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-


Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q18) Evaluate the integral given below by using Cauchy’s integral formula-

A18)
Here we have-
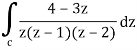
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q19) Evaluate 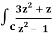 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
A19)
Here we have-

Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
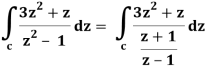 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q20) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A20)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q21) Find the singularity of the function-
f(z) = sin 1/z
A21)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q22) Show that when 0<|z|<4
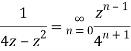
A22)
When |z|<4 we have
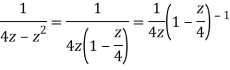

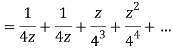
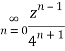
Q23) Find the residue of 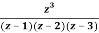 at z=1
at z=1
A23)
Let f(z)=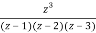
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=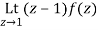

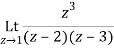
=1/2
Unit - 5
Complex Variable - Differentiation
Q1) Find-
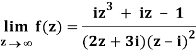
A1)
Here we have-
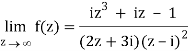
Divide numerator and denominator by z3, we get-
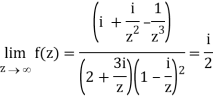
Q2) If f(z) is a complex function given below, then discuss dz/dz at z = 0
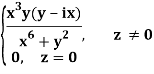
A2)
If z→0 along radius vector y = mx
= 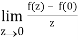
= 
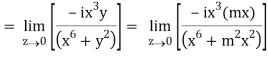

But along v = x3,
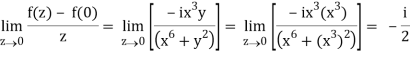
In different paths we get different value of df/dz that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Q3) Prove: The necessary condition for a function 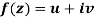 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
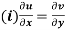 (ii)
(ii) 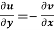
Provided, 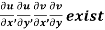
A3)
Let 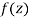 be an analytic function in region R.
be an analytic function in region R.
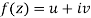
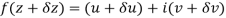

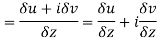
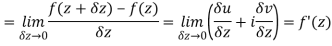
Along real axis

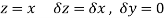
Then f’(z), becomes-
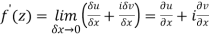 ………… (1)
………… (1)
Along imaginary axis


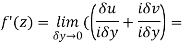

From equation (1) and (2)
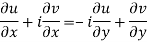
Equating real and imaginary parts

Therefore-
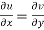 and
and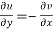
These are called Cauchy Riemann Equations.
Q4) What is Analytic function and write is necessary conditions?
A4)
A function  is said to be analytic at a point
is said to be analytic at a point 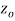 if f is differentiable not only at
if f is differentiable not only at 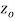 but every point of some neighborhood at
but every point of some neighborhood at 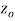 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 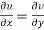 …………. (1)
…………. (1)
2.  ……...…. (2)
……...…. (2)
Provided  exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1.  …………. (1)
…………. (1)
2. 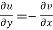 ……...…. (2)
……...…. (2)
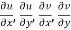 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Q5) State and prove sufficient condition for analytic functions
A5)
Statement – The sufficient condition for a function 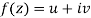 to be analytic at all points in a region R are
to be analytic at all points in a region R are
1. 
2. 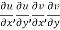 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having  at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
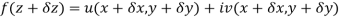
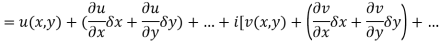
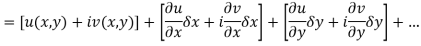
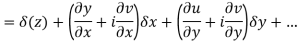
Ignoring the terms of second power and higher power
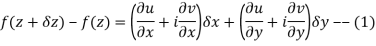
We know C-R equation

Replacing 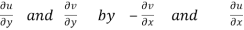
Respectively in (1) we get
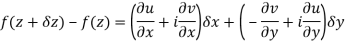
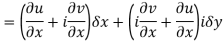
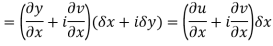
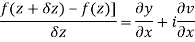
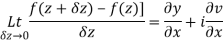
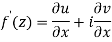
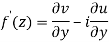
Q6) Show that  is analytic at
is analytic at 
A6)
The function f(z) is analytic at  if the function
if the function  is analytic at z=0
is analytic at z=0
Since 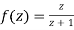
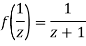
Now 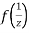 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 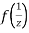 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 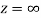
Q7) If w = log z, then find  . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A7)
Here we have 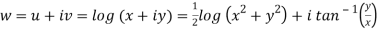
Therefore-
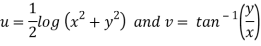
 and
and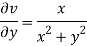
Again-
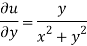
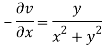
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
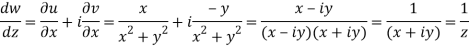
Q8) Prove that the function 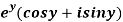 is an analytical function.
is an analytical function.
A8)
Let 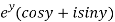 =u+iv
=u+iv
Let 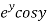 =u and
=u and 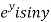 =v
=v

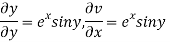
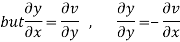
Hence C-R-Equation satisfied.
Q9) Prove that 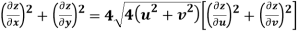
A9)
Given that
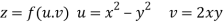
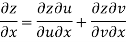
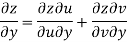
Since 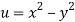

V=2xy

Now 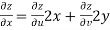
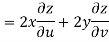
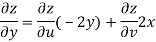
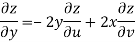

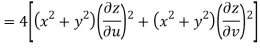
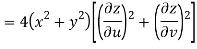
But 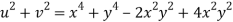

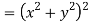

Hence 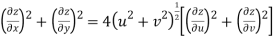
Q10) Show that polar form of C-R equations are-

A10)
z = x + iy = 

U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
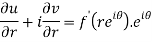
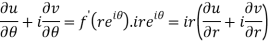
By equating real and imaginary parts, we get-
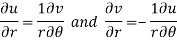
Q11) Prove Harmonic function theorem.
A11)
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
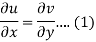

Differentiate (1) with respect to x, we get
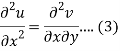
Differentiate (2) with respect to y, we get
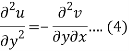
Add 3 and 4-
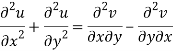

Similarly-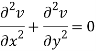
So that u and v are harmonic functions.
Q12) Prove that 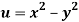 and
and  are harmonic functions of (x, y).
are harmonic functions of (x, y).
A12)
We have 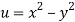
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
2v/x2 = 
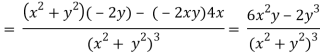
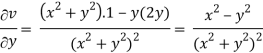
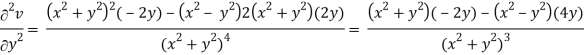

On adding the above results-
We get-

So that v(x, y) is also a harmonic function.
Q13) Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A13)
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
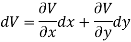

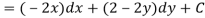
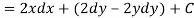
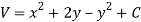
Hence the harmonic conjugate of U is 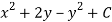
Q14) Solve 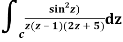 where
where 
A14)
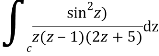
Where 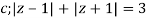
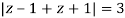
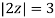
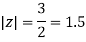
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1

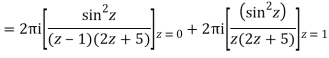

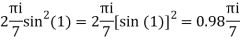
Q15) Solve 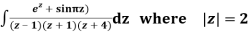
A15)

Poles are
|z-0|=2
Poles 1 and -1 inside the circle
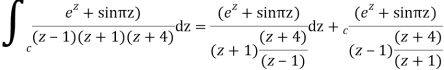
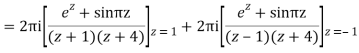
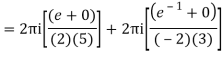


Q16) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 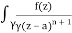
A16)
Given,
f(n)(a) = n!/2πi 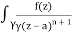
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 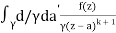
= k!/2πi 
= (k+1)!/2πi 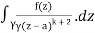
Q17) Evaluate 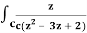 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A17)
It is given that-
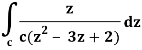
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-

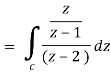
Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q18) Evaluate the integral given below by using Cauchy’s integral formula-

A18)
Here we have-

Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
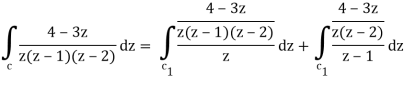 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q19) Evaluate 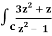 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
A19)
Here we have-
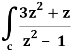
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
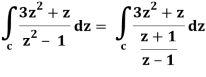 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q20) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A20)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q21) Find the singularity of the function-
f(z) = sin 1/z
A21)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q22) Show that when 0<|z|<4

A22)
When |z|<4 we have
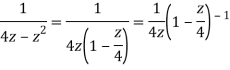
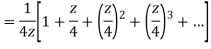
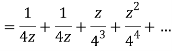

Q23) Find the residue of 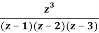 at z=1
at z=1
A23)
Let f(z)=
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=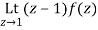

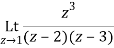
=1/2
Unit - 5
Unit - 5
Complex Variable - Differentiation
Q1) Find-

A1)
Here we have-
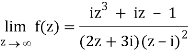
Divide numerator and denominator by z3, we get-

Q2) If f(z) is a complex function given below, then discuss dz/dz at z = 0
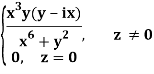
A2)
If z→0 along radius vector y = mx
= 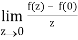
= 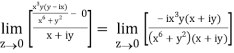
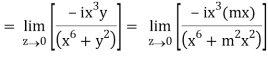
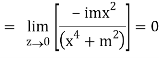
But along v = x3,
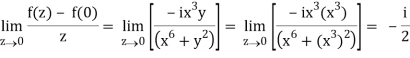
In different paths we get different value of df/dz that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Q3) Prove: The necessary condition for a function  to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
 (ii)
(ii) 
Provided, 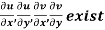
A3)
Let 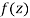 be an analytic function in region R.
be an analytic function in region R.

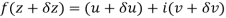
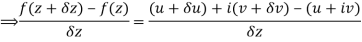
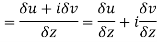
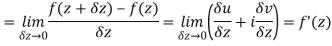
Along real axis


Then f’(z), becomes-
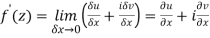 ………… (1)
………… (1)
Along imaginary axis
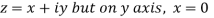
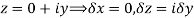
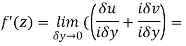
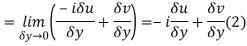
From equation (1) and (2)

Equating real and imaginary parts

Therefore-
 and
and
These are called Cauchy Riemann Equations.
Q4) What is Analytic function and write is necessary conditions?
A4)
A function 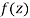 is said to be analytic at a point
is said to be analytic at a point 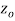 if f is differentiable not only at
if f is differentiable not only at 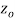 but every point of some neighborhood at
but every point of some neighborhood at 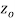 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 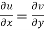 …………. (1)
…………. (1)
2. 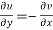 ……...…. (2)
……...…. (2)
Provided 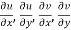 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 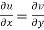 …………. (1)
…………. (1)
2. 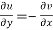 ……...…. (2)
……...…. (2)
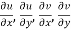 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Q5) State and prove sufficient condition for analytic functions
A5)
Statement – The sufficient condition for a function  to be analytic at all points in a region R are
to be analytic at all points in a region R are
1. 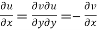
2. 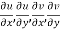 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having  at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
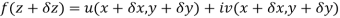

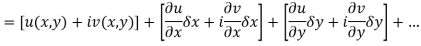
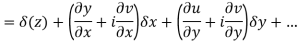
Ignoring the terms of second power and higher power
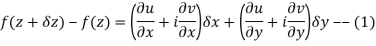
We know C-R equation

Replacing 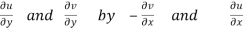
Respectively in (1) we get
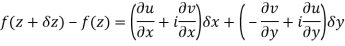
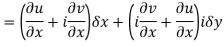
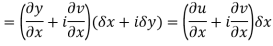

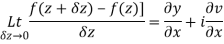

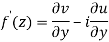
Q6) Show that 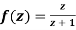 is analytic at
is analytic at 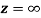
A6)
The function f(z) is analytic at  if the function
if the function  is analytic at z=0
is analytic at z=0
Since 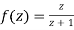
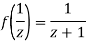
Now 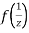 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 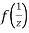 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 
Q7) If w = log z, then find  . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A7)
Here we have 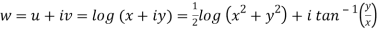
Therefore-
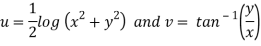
 and
and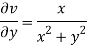
Again-
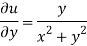
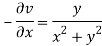
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
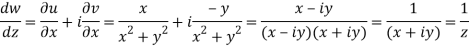
Q8) Prove that the function 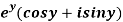 is an analytical function.
is an analytical function.
A8)
Let 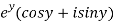 =u+iv
=u+iv
Let  =u and
=u and 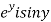 =v
=v

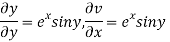
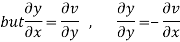
Hence C-R-Equation satisfied.
Q9) Prove that 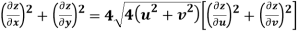
A9)
Given that



Since 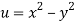

V=2xy

Now 

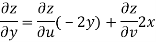
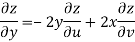
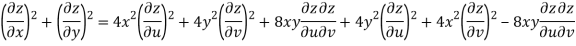

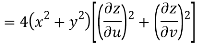
But 

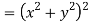
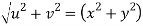
Hence 
Q10) Show that polar form of C-R equations are-
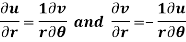
A10)
z = x + iy = 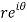
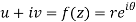
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
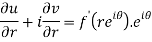
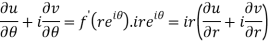
By equating real and imaginary parts, we get-
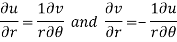
Q11) Prove Harmonic function theorem.
A11)
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have

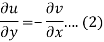
Differentiate (1) with respect to x, we get
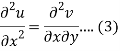
Differentiate (2) with respect to y, we get

Add 3 and 4-
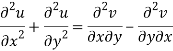
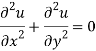
Similarly-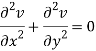
So that u and v are harmonic functions.
Q12) Prove that 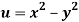 and
and 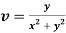 are harmonic functions of (x, y).
are harmonic functions of (x, y).
A12)
We have 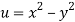
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
2v/x2 = 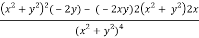
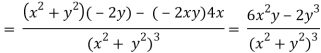

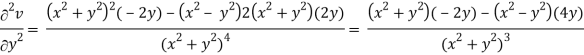
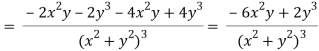
On adding the above results-
We get-
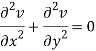
So that v(x, y) is also a harmonic function.
Q13) Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A13)
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
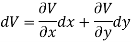
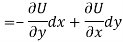
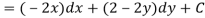


Hence the harmonic conjugate of U is 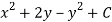
Q14) Solve 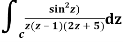 where
where 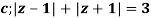
A14)

Where 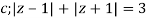

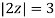
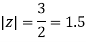
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
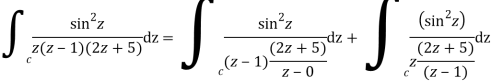
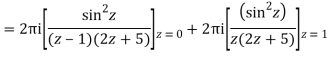


Q15) Solve 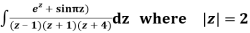
A15)
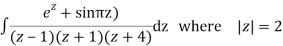
Poles are
|z-0|=2
Poles 1 and -1 inside the circle


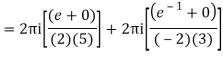
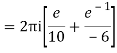

Q16) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 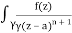
A16)
Given,
f(n)(a) = n!/2πi 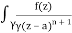
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 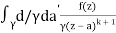
= k!/2πi 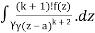
= (k+1)!/2πi 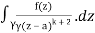
Q17) Evaluate  dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A17)
It is given that-
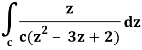
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-


Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q18) Evaluate the integral given below by using Cauchy’s integral formula-

A18)
Here we have-

Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
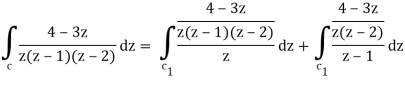 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q19) Evaluate  dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
A19)
Here we have-

Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
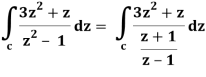 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q20) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A20)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q21) Find the singularity of the function-
f(z) = sin 1/z
A21)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q22) Show that when 0<|z|<4

A22)
When |z|<4 we have

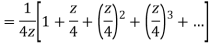
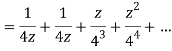
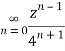
Q23) Find the residue of 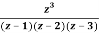 at z=1
at z=1
A23)
Let f(z)=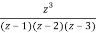
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=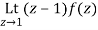

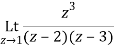
=1/2
Unit - 5
Unit - 5
Unit - 5
Complex Variable - Differentiation
Q1) Find-
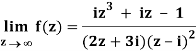
A1)
Here we have-

Divide numerator and denominator by z3, we get-
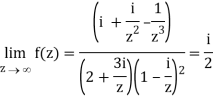
Q2) If f(z) is a complex function given below, then discuss dz/dz at z = 0
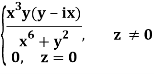
A2)
If z→0 along radius vector y = mx
= 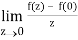
= 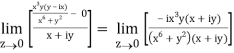
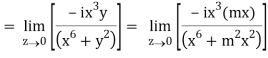
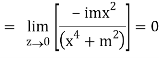
But along v = x3,
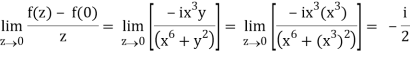
In different paths we get different value of df/dz that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Q3) Prove: The necessary condition for a function  to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
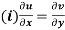 (ii)
(ii) 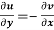
Provided, 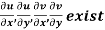
A3)
Let 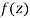 be an analytic function in region R.
be an analytic function in region R.
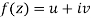
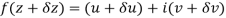
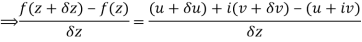
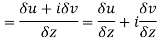

Along real axis
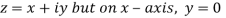
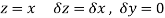
Then f’(z), becomes-
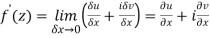 ………… (1)
………… (1)
Along imaginary axis


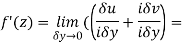
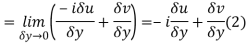
From equation (1) and (2)
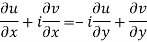
Equating real and imaginary parts
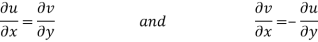
Therefore-
 and
and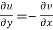
These are called Cauchy Riemann Equations.
Q4) What is Analytic function and write is necessary conditions?
A4)
A function 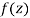 is said to be analytic at a point
is said to be analytic at a point 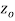 if f is differentiable not only at
if f is differentiable not only at  but every point of some neighborhood at
but every point of some neighborhood at 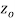 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1.  …………. (1)
…………. (1)
2.  ……...…. (2)
……...…. (2)
Provided 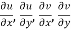 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1.  …………. (1)
…………. (1)
2.  ……...…. (2)
……...…. (2)
 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Q5) State and prove sufficient condition for analytic functions
A5)
Statement – The sufficient condition for a function  to be analytic at all points in a region R are
to be analytic at all points in a region R are
1. 
2. 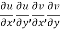 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having 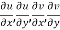 at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem

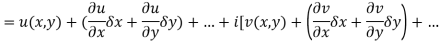
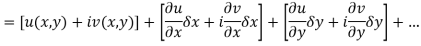
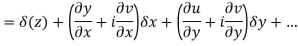
Ignoring the terms of second power and higher power

We know C-R equation
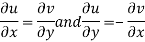
Replacing 
Respectively in (1) we get
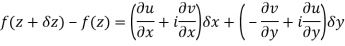
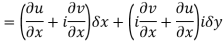

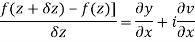
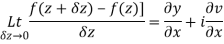
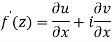
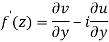
Q6) Show that  is analytic at
is analytic at 
A6)
The function f(z) is analytic at  if the function
if the function 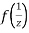 is analytic at z=0
is analytic at z=0
Since 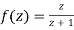
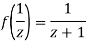
Now 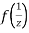 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 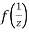 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 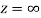
Q7) If w = log z, then find 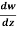 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A7)
Here we have 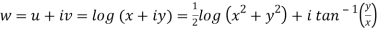
Therefore-
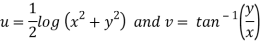
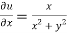 and
and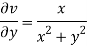
Again-
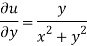
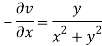
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0

Q8) Prove that the function  is an analytical function.
is an analytical function.
A8)
Let  =u+iv
=u+iv
Let 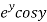 =u and
=u and  =v
=v
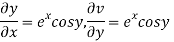

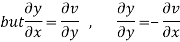
Hence C-R-Equation satisfied.
Q9) Prove that 
A9)
Given that

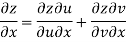

Since 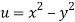

V=2xy

Now 

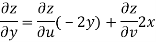
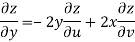
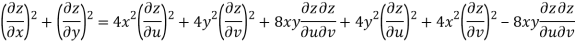
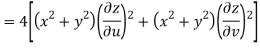

But 
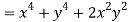

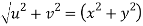
Hence 
Q10) Show that polar form of C-R equations are-
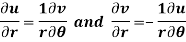
A10)
z = x + iy = 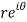
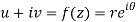
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-

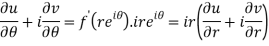
By equating real and imaginary parts, we get-

Q11) Prove Harmonic function theorem.
A11)
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
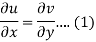

Differentiate (1) with respect to x, we get
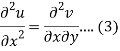
Differentiate (2) with respect to y, we get
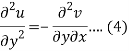
Add 3 and 4-
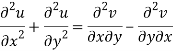

Similarly-
So that u and v are harmonic functions.
Q12) Prove that 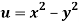 and
and 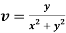 are harmonic functions of (x, y).
are harmonic functions of (x, y).
A12)
We have 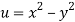
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
2v/x2 = 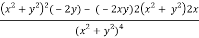
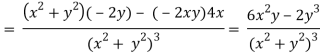
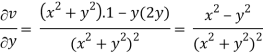


On adding the above results-
We get-

So that v(x, y) is also a harmonic function.
Q13) Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A13)
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
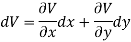
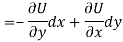

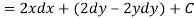
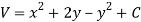
Hence the harmonic conjugate of U is 
Q14) Solve  where
where 
A14)
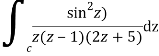
Where 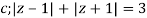
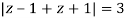
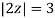
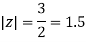
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
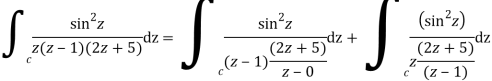
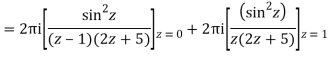
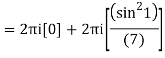

Q15) Solve 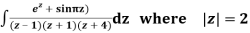
A15)

Poles are
|z-0|=2
Poles 1 and -1 inside the circle
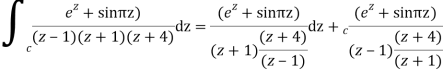

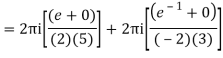
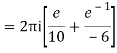
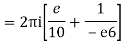
Q16) Solve the following by cauchy’s integral method:
f(n)(a) = n!/2πi 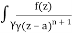
A16)
Given,
f(n)(a) = n!/2πi 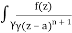
f(k + 1)(a) = d/da f(k)(a)
= k!/2πi 
= k!/2πi 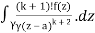
= (k+1)!/2πi 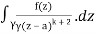
Q17) Evaluate 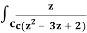 dz by using Cauchy’s integral formula.
dz by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
A17)
It is given that-
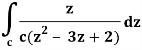
Find its poles by equating denominator equals to zero.
z2 – 3z + 2 = 0
(z – 1)(z – 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
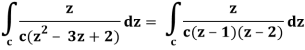
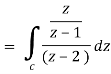
Now by using Cauchy’s integral formula, we get-
= 2πi [ z / z-1]z = 2 = 2πi(2/2 -1) = 4πi
Q18) Evaluate the integral given below by using Cauchy’s integral formula-

A18)
Here we have-
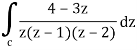
Find its poles by equating denominator equals to zero.
z(z – 1)(z – 2) = 0
We get-
z = 0,1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
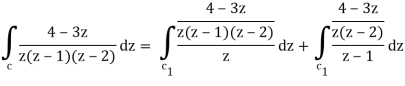 = 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2 πi [ (4 – 3z)/(z – 1)(z – 2)]z=0 + 2πi [(4 – 3z)/z(z-2)]z = 1
= 2πi . 4/(-1)(-2) + 2πi (4 -3)/1(1 -2) = 2πi(2 – 1) = 2πi
Q19) Evaluate 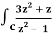 dz if c is circle |z - 1| = 1.
dz if c is circle |z - 1| = 1.
A19)
Here we have-
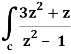
Find its poles by equating denominator equals to zero.
z2 – 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
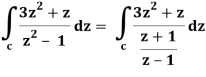 = 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 2πi [(3z2 + z)/(z+1)]z = 1 = 2πi((3+1)/(1+1))
= 4πi
Q20) Find out the zero of the following-
f(z) = (z – 2)/z2 sin 1/(z – 1)
A20)
Zeroes of the function-
f(z) = 0
(z – 2)/z2 sin 1/(z – 1) = 0
(z – 2)/z2 = 0, sin 1/(z – 1) = 0
z = 2, 1/(z – 1) = nπ ( n = 0, ±1, ±2 ….)
z = 2, 1 + 1/nπ (n = 0, ±1, ±2 ….)
Q21) Find the singularity of the function-
f(z) = sin 1/z
A21)
As we know that-f(z) = a0 +a1(z – a) + a2(z – a)2 + . . . + 1/(z – a)m[ b1(z – a)m – 1 + b2(z – a)m – 2 + b3(z – a)m – 3 + . . . + bm}
So that there is a number of singularity.
Sin 1/z is not analytic at z = a
(1/z = ∞ at z = 0)
Q22) Show that when 0<|z|<4
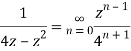
A22)
When |z|<4 we have

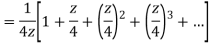
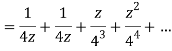
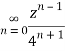
Q23) Find the residue of  at z=1
at z=1
A23)
Let f(z)=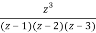
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=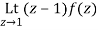

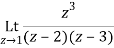
=1/2