Unit - 4
Probability and Statistics
Q1) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
A1)
Let be the number of heads in the toss of three coins
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P[X= 0] = P[TTT] = 1/8
P[X = 1] = P [HTT, THH, TTH] = 3/8
P[X = 2] = P[HHT, HTH, THH] = 3/8
P[X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X | 0 | 1 | 2 | 3 |
P(x) | 1/8 | 3/8 | 3/8 | 1/8 |
Q2) For the following probability distribution of a discrete random variable X,
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Find-
1. The value of c.
2. P[1<x<4]
A2)
We know that-
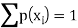
So that-
0 + c + c + 2c + 3c + c = 1
8c = 1
Then c = 1/8
Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8
Q3) Show that the following function can be defined as a density function and then find P(1 ≤ x ≤ 2).
A3)
f(x) = e-x x ≥ 0
= 0 x < 0
Sol.
Here
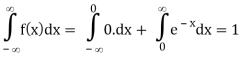
So that, the function can be defined as a density function.
Now.
P(1 ≤ x ≤ 2) = 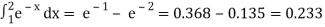
Q4) Two discrete random variables X and Y have-
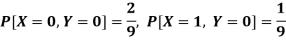
And
P[X = 1, Y = 1] = 5/9.
Check whether X and Y are independent or not?
A4)
First, we write the given distribution In tabular form-
X/Y | 0 | 1 | P(x) |
0 | 2/9 | 1/9 | 3/9 |
1 | 1/9 | 5/9 | 6/9 |
P(y) | 3/9 | 6/9 | 1 |
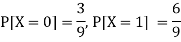
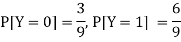
Now-

But

So that-
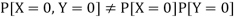
Hence X and Y are not independent.
Q5) A random variable x has the following probability distribution-
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Then find-
1. Value of c.
2. P[X≤3]
3. P[1 < X <4]
A5)
We know that for the given probability distribution-
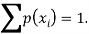
So that-
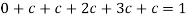
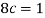
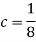
2.


3.
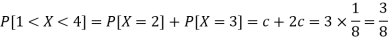
Q6) In a lottery, m tickets are drawn at a time out of tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
A6)
Let 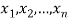 be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
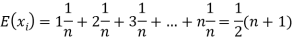
Therefore the expected value of the sum of the numbers on the tickets drawn

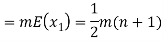
Q7) X is a continuous random variable with probability density function given by

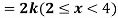
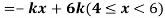
Find k and mean value of X.
A7)
Since the total probability is unity.
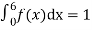


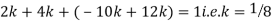
Mean of X =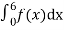
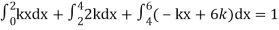
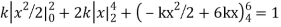


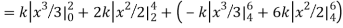
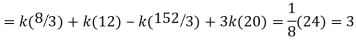
Q8) The frequency distribution of a measurable characteristic varying between 0 and 2 is as under
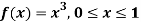
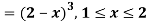
Calculate two standard deviations and also the mean deviation about the mean.
A8)
Total frequency N =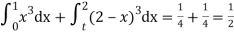
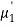 (about the origin)=
(about the origin)=
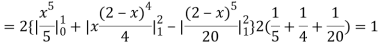
 (about the origin)=
(about the origin)= 
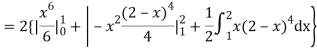
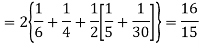
Hence, 
i.e., standard deviation 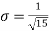
Mean derivation about the mean
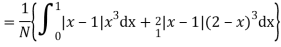
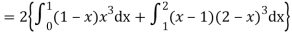

Q9) If a random variable X has the following probability distribution in the tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
A9)
We know that-
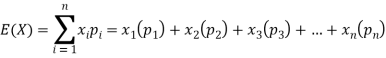
So that-

Q10) Find the expectations of the number of an unbiased die when thrown.
A10)
Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-

So that-

Q11) I roll a fair die and let X be the resulting number. Find E(X), Var(X), and 
A11)
We have  and
and 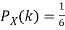 for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have
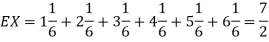

Thus,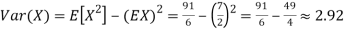
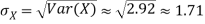
Q12) If on average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
A12)
Out of 10 ships, one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 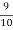
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)
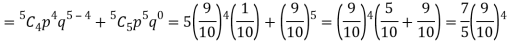
Q13) The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?
A13)
Probability of failures = 20% 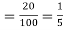
Probability of (P) = 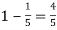
Probability of at least 5 passes = P(5 or 6)

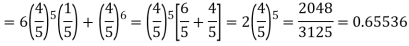
Q14) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?
A14)
The probability that a man aged 60 will live to be 70
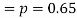

Number of men= n = 10
Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)
= P (7)+ P(8)+ P(9) + P(10) =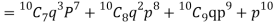

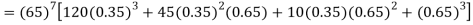
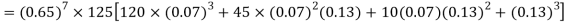
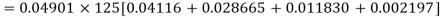

Q15) Find the mean and variance of a binomial distribution with p = 1/4 and n = 10.
A15)
Here 
Mean = np = 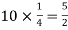
Variance = npq = 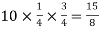
Q16) Assume that the probability of an individual coal miner being killed in a mine accident during a year is  . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
A16)
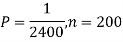
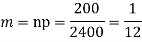
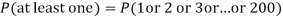
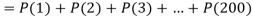
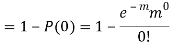
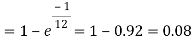
Q17) Suppose 3% of bolts made by a machine are defective, the defects occurring at random during production. If bolts are packaged 50 per box, find
(a) Exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
A17)
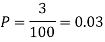
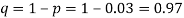
(a) Hence the probability for 5 defectives bolts in a lot of 50.
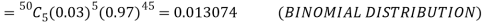
(b) To get Poisson approximation m = np =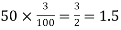
Required Poisson approximation=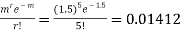
Q18) On a final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard scores of students receiving grades.
(a) 60
(b) 93
(c) 72
A18)
(a) 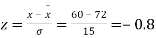
(b)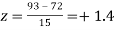
(c) 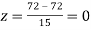
Q19) Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
A19)
(a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Q20) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise, the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.
A20)

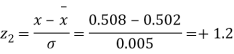
Area for non – defective washers = Area between z = -1.2
And z = +1.2
=2 Area between z = 0 and z = 1.2
=2 (0.3849)-0.7698=76.98%
(0.3849)-0.7698=76.98%
Percentage of defective washers = 100-76.98=23.02%
Q21) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 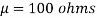 and standard deviation
and standard deviation 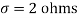 . What percentage of resistors will have resistance between 98 ohms and 102 ohms?
. What percentage of resistors will have resistance between 98 ohms and 102 ohms?
A21)
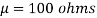 ,
,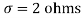
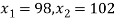

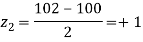
Area between 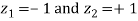
= (Area between z = 0 and z = +1)
= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826
0.3413 = 0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26
Q22) In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
A22)
Let 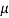 be the mean and
be the mean and 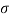 the S.D.
the S.D.
If x = 45, 
If x = 64, 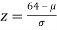
The area between 0 and 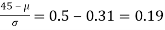
[From the table, for the area 0.19, z = 0.496)
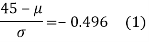
Area between z = 0 and z =
(from the table for area 0.42, z = 1.405)
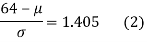
Solving (1) and (2) we get 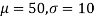
Q23) If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
A23)
The standard normal variate is –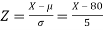
Now-
1. X = 95,
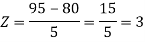
So that-
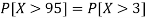
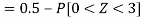
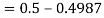
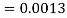
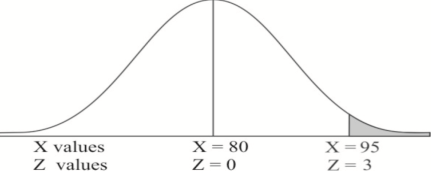
2. X = 72,

So that-
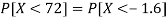

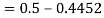
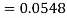

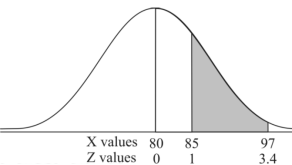
3. X = 85,
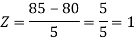
X = 97,

So that-
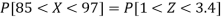

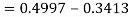
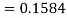
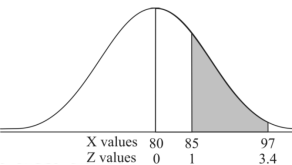
Q24) If a continuous random variable X has the following probability density function:
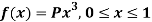
Then find-
1. P[0.2 < X < 0.5]
A24)
Here f(x) is the probability density function, then-

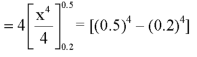
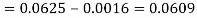
Q25) The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 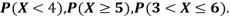
(ii) What will be e minimum value of k so that 
A25)
(i) If X is a random variable then
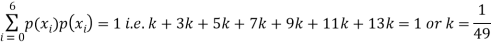
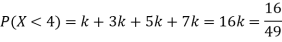

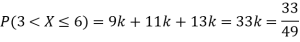
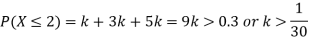
(ii)Thus minimum value of k=1/30.
Unit - 4
Probability and Statistics
Q1) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
A1)
Let be the number of heads in the toss of three coins
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P[X= 0] = P[TTT] = 1/8
P[X = 1] = P [HTT, THH, TTH] = 3/8
P[X = 2] = P[HHT, HTH, THH] = 3/8
P[X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X | 0 | 1 | 2 | 3 |
P(x) | 1/8 | 3/8 | 3/8 | 1/8 |
Q2) For the following probability distribution of a discrete random variable X,
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Find-
1. The value of c.
2. P[1<x<4]
A2)
We know that-
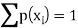
So that-
0 + c + c + 2c + 3c + c = 1
8c = 1
Then c = 1/8
Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8
Q3) Show that the following function can be defined as a density function and then find P(1 ≤ x ≤ 2).
A3)
f(x) = e-x x ≥ 0
= 0 x < 0
Sol.
Here
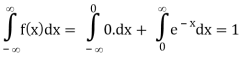
So that, the function can be defined as a density function.
Now.
P(1 ≤ x ≤ 2) = 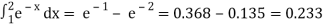
Q4) Two discrete random variables X and Y have-
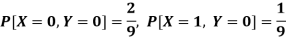
And
P[X = 1, Y = 1] = 5/9.
Check whether X and Y are independent or not?
A4)
First, we write the given distribution In tabular form-
X/Y | 0 | 1 | P(x) |
0 | 2/9 | 1/9 | 3/9 |
1 | 1/9 | 5/9 | 6/9 |
P(y) | 3/9 | 6/9 | 1 |
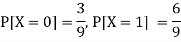

Now-

But
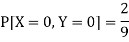
So that-
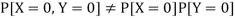
Hence X and Y are not independent.
Q5) A random variable x has the following probability distribution-
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Then find-
1. Value of c.
2. P[X≤3]
3. P[1 < X <4]
A5)
We know that for the given probability distribution-
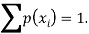
So that-
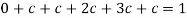
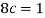
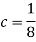
2.

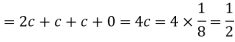
3.
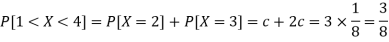
Q6) In a lottery, m tickets are drawn at a time out of tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
A6)
Let 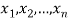 be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have

Therefore the expected value of the sum of the numbers on the tickets drawn
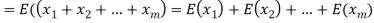
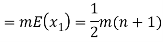
Q7) X is a continuous random variable with probability density function given by
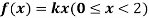
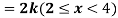
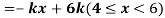
Find k and mean value of X.
A7)
Since the total probability is unity.

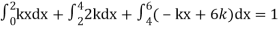
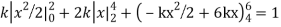
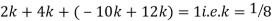
Mean of X =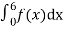
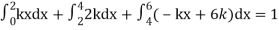
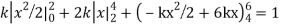
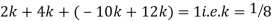

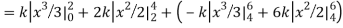
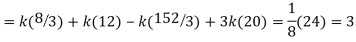
Q8) The frequency distribution of a measurable characteristic varying between 0 and 2 is as under
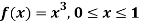

Calculate two standard deviations and also the mean deviation about the mean.
A8)
Total frequency N =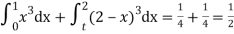
 (about the origin)=
(about the origin)=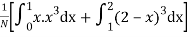

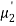 (about the origin)=
(about the origin)= 
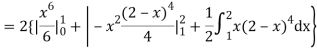
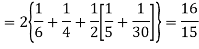
Hence, 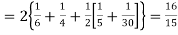
i.e., standard deviation 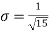
Mean derivation about the mean
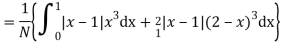


Q9) If a random variable X has the following probability distribution in the tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
A9)
We know that-

So that-
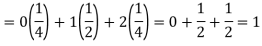
Q10) Find the expectations of the number of an unbiased die when thrown.
A10)
Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-

So that-
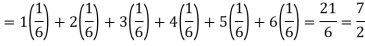
Q11) I roll a fair die and let X be the resulting number. Find E(X), Var(X), and 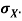
A11)
We have 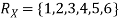 and
and 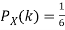 for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have
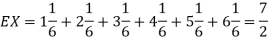

Thus,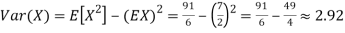
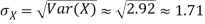
Q12) If on average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
A12)
Out of 10 ships, one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 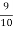
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)
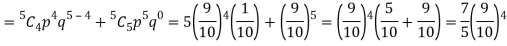
Q13) The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?
A13)
Probability of failures = 20% 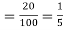
Probability of (P) = 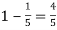
Probability of at least 5 passes = P(5 or 6)

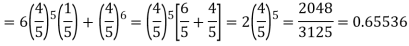
Q14) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?
A14)
The probability that a man aged 60 will live to be 70
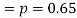

Number of men= n = 10
Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)
= P (7)+ P(8)+ P(9) + P(10) =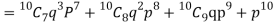

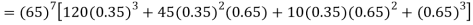
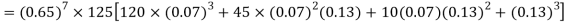

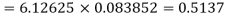
Q15) Find the mean and variance of a binomial distribution with p = 1/4 and n = 10.
A15)
Here 
Mean = np = 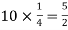
Variance = npq = 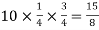
Q16) Assume that the probability of an individual coal miner being killed in a mine accident during a year is 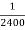 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
A16)
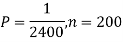


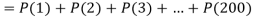
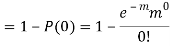
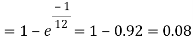
Q17) Suppose 3% of bolts made by a machine are defective, the defects occurring at random during production. If bolts are packaged 50 per box, find
(a) Exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
A17)

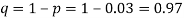
(a) Hence the probability for 5 defectives bolts in a lot of 50.
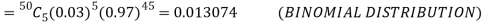
(b) To get Poisson approximation m = np =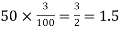
Required Poisson approximation=
Q18) On a final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard scores of students receiving grades.
(a) 60
(b) 93
(c) 72
A18)
(a) 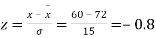
(b)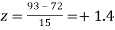
(c) 
Q19) Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
A19)
(a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Q20) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise, the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.
A20)
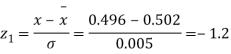
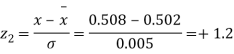
Area for non – defective washers = Area between z = -1.2
And z = +1.2
=2 Area between z = 0 and z = 1.2
=2 (0.3849)-0.7698=76.98%
(0.3849)-0.7698=76.98%
Percentage of defective washers = 100-76.98=23.02%
Q21) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 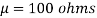 and standard deviation
and standard deviation  . What percentage of resistors will have resistance between 98 ohms and 102 ohms?
. What percentage of resistors will have resistance between 98 ohms and 102 ohms?
A21)
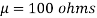 ,
,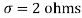
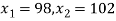
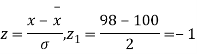

Area between 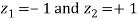
= (Area between z = 0 and z = +1)
= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826
0.3413 = 0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26
Q22) In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
A22)
Let 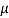 be the mean and
be the mean and 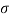 the S.D.
the S.D.
If x = 45, 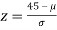
If x = 64, 
The area between 0 and 
[From the table, for the area 0.19, z = 0.496)
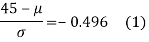
Area between z = 0 and z =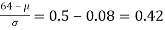
(from the table for area 0.42, z = 1.405)
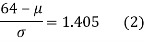
Solving (1) and (2) we get 
Q23) If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
A23)
The standard normal variate is –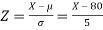
Now-
1. X = 95,
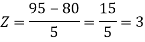
So that-
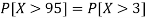
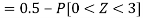
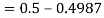
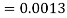

2. X = 72,

So that-
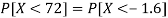

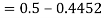


3. X = 85,
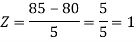
X = 97,
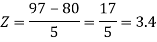
So that-
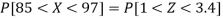

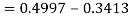

Q24) If a continuous random variable X has the following probability density function:
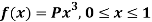
Then find-
1. P[0.2 < X < 0.5]
A24)
Here f(x) is the probability density function, then-
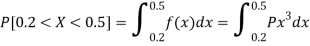
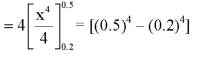
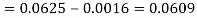
Q25) The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 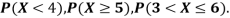
(ii) What will be e minimum value of k so that 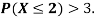
A25)
(i) If X is a random variable then
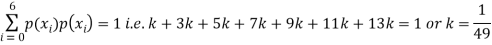
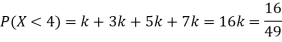
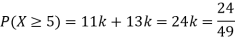

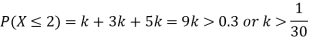
(ii)Thus minimum value of k=1/30.
Unit - 4
Unit - 4
Unit - 4
Unit - 4
Unit - 4
Unit - 4
Probability and Statistics
Q1) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
A1)
Let be the number of heads in the toss of three coins
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P[X= 0] = P[TTT] = 1/8
P[X = 1] = P [HTT, THH, TTH] = 3/8
P[X = 2] = P[HHT, HTH, THH] = 3/8
P[X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X | 0 | 1 | 2 | 3 |
P(x) | 1/8 | 3/8 | 3/8 | 1/8 |
Q2) For the following probability distribution of a discrete random variable X,
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Find-
1. The value of c.
2. P[1<x<4]
A2)
We know that-
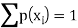
So that-
0 + c + c + 2c + 3c + c = 1
8c = 1
Then c = 1/8
Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8
Q3) Show that the following function can be defined as a density function and then find P(1 ≤ x ≤ 2).
A3)
f(x) = e-x x ≥ 0
= 0 x < 0
Sol.
Here

So that, the function can be defined as a density function.
Now.
P(1 ≤ x ≤ 2) = 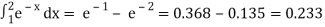
Q4) Two discrete random variables X and Y have-

And
P[X = 1, Y = 1] = 5/9.
Check whether X and Y are independent or not?
A4)
First, we write the given distribution In tabular form-
X/Y | 0 | 1 | P(x) |
0 | 2/9 | 1/9 | 3/9 |
1 | 1/9 | 5/9 | 6/9 |
P(y) | 3/9 | 6/9 | 1 |

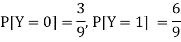
Now-
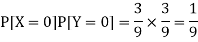
But
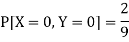
So that-
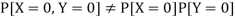
Hence X and Y are not independent.
Q5) A random variable x has the following probability distribution-
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Then find-
1. Value of c.
2. P[X≤3]
3. P[1 < X <4]
A5)
We know that for the given probability distribution-
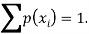
So that-
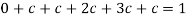
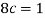
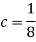
2.
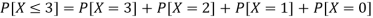

3.
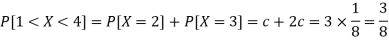
Q6) In a lottery, m tickets are drawn at a time out of tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
A6)
Let 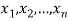 be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
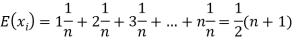
Therefore the expected value of the sum of the numbers on the tickets drawn
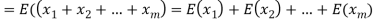
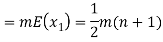
Q7) X is a continuous random variable with probability density function given by
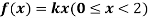
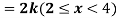
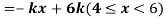
Find k and mean value of X.
A7)
Since the total probability is unity.
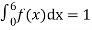
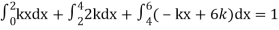
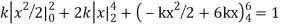

Mean of X =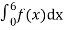

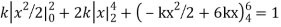
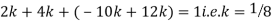
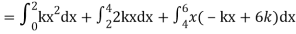
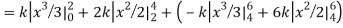
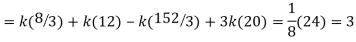
Q8) The frequency distribution of a measurable characteristic varying between 0 and 2 is as under
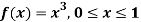
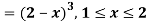
Calculate two standard deviations and also the mean deviation about the mean.
A8)
Total frequency N =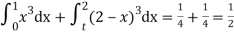
 (about the origin)=
(about the origin)=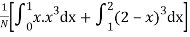

 (about the origin)=
(about the origin)= 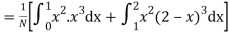
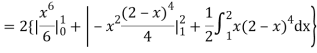
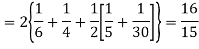
Hence, 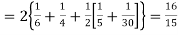
i.e., standard deviation 
Mean derivation about the mean

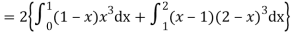
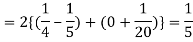
Q9) If a random variable X has the following probability distribution in the tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
A9)
We know that-
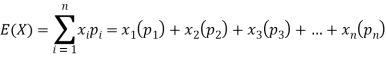
So that-
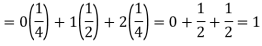
Q10) Find the expectations of the number of an unbiased die when thrown.
A10)
Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
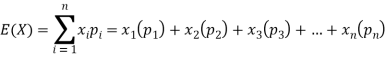
So that-
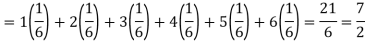
Q11) I roll a fair die and let X be the resulting number. Find E(X), Var(X), and 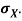
A11)
We have 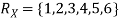 and
and  for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have
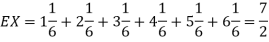
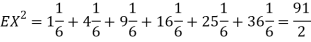
Thus,
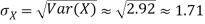
Q12) If on average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
A12)
Out of 10 ships, one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 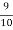
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)
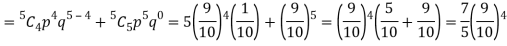
Q13) The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?
A13)
Probability of failures = 20% 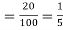
Probability of (P) = 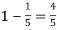
Probability of at least 5 passes = P(5 or 6)
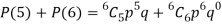

Q14) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?
A14)
The probability that a man aged 60 will live to be 70
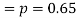

Number of men= n = 10
Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)
= P (7)+ P(8)+ P(9) + P(10) =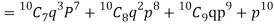
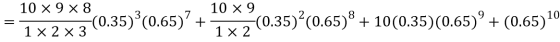
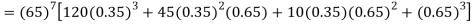
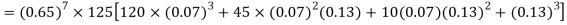
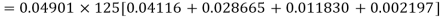
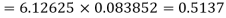
Q15) Find the mean and variance of a binomial distribution with p = 1/4 and n = 10.
A15)
Here 
Mean = np = 
Variance = npq = 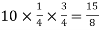
Q16) Assume that the probability of an individual coal miner being killed in a mine accident during a year is 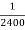 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
A16)



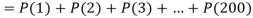
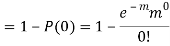
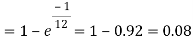
Q17) Suppose 3% of bolts made by a machine are defective, the defects occurring at random during production. If bolts are packaged 50 per box, find
(a) Exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
A17)
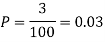
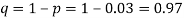
(a) Hence the probability for 5 defectives bolts in a lot of 50.
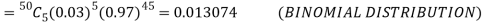
(b) To get Poisson approximation m = np =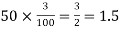
Required Poisson approximation=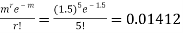
Q18) On a final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard scores of students receiving grades.
(a) 60
(b) 93
(c) 72
A18)
(a) 
(b)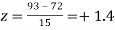
(c) 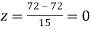
Q19) Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
A19)
(a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Q20) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise, the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.
A20)
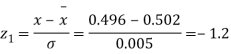
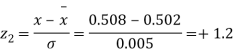
Area for non – defective washers = Area between z = -1.2
And z = +1.2
=2 Area between z = 0 and z = 1.2
=2 (0.3849)-0.7698=76.98%
(0.3849)-0.7698=76.98%
Percentage of defective washers = 100-76.98=23.02%
Q21) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean  and standard deviation
and standard deviation  . What percentage of resistors will have resistance between 98 ohms and 102 ohms?
. What percentage of resistors will have resistance between 98 ohms and 102 ohms?
A21)
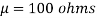 ,
,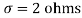

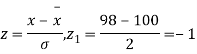
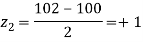
Area between 
= (Area between z = 0 and z = +1)
= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826
0.3413 = 0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26
Q22) In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
A22)
Let 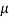 be the mean and
be the mean and 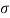 the S.D.
the S.D.
If x = 45, 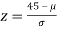
If x = 64, 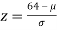
The area between 0 and 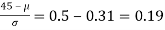
[From the table, for the area 0.19, z = 0.496)
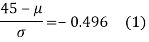
Area between z = 0 and z =
(from the table for area 0.42, z = 1.405)

Solving (1) and (2) we get 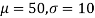
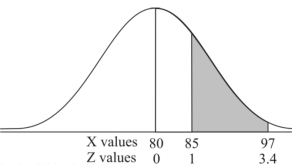
Q23) If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
A23)
The standard normal variate is –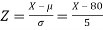
Now-
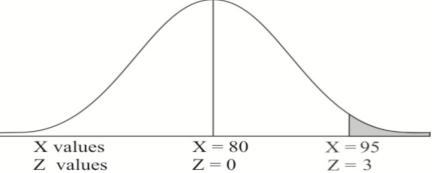
1. X = 95,
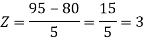
So that-
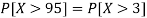
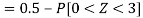
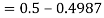

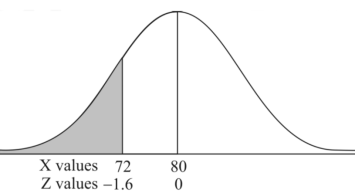
2. X = 72,
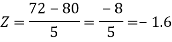
So that-




3. X = 85,
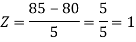
X = 97,
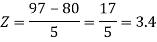
So that-

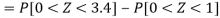
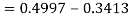
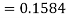
Q24) If a continuous random variable X has the following probability density function:
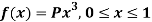
Then find-
1. P[0.2 < X < 0.5]
A24)
Here f(x) is the probability density function, then-
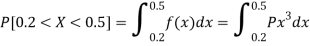
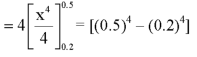

Q25) The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 
(ii) What will be e minimum value of k so that 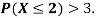
A25)
(i) If X is a random variable then
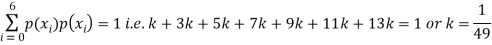


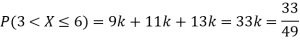
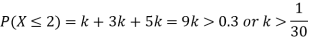
(ii)Thus minimum value of k=1/30.
Unit - 4
Probability and Statistics
Q1) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
A1)
Let be the number of heads in the toss of three coins
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P[X= 0] = P[TTT] = 1/8
P[X = 1] = P [HTT, THH, TTH] = 3/8
P[X = 2] = P[HHT, HTH, THH] = 3/8
P[X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X | 0 | 1 | 2 | 3 |
P(x) | 1/8 | 3/8 | 3/8 | 1/8 |
Q2) For the following probability distribution of a discrete random variable X,
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Find-
1. The value of c.
2. P[1<x<4]
A2)
We know that-
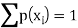
So that-
0 + c + c + 2c + 3c + c = 1
8c = 1
Then c = 1/8
Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8
Q3) Show that the following function can be defined as a density function and then find P(1 ≤ x ≤ 2).
A3)
f(x) = e-x x ≥ 0
= 0 x < 0
Sol.
Here
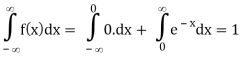
So that, the function can be defined as a density function.
Now.
P(1 ≤ x ≤ 2) = 
Q4) Two discrete random variables X and Y have-
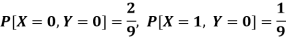
And
P[X = 1, Y = 1] = 5/9.
Check whether X and Y are independent or not?
A4)
First, we write the given distribution In tabular form-
X/Y | 0 | 1 | P(x) |
0 | 2/9 | 1/9 | 3/9 |
1 | 1/9 | 5/9 | 6/9 |
P(y) | 3/9 | 6/9 | 1 |
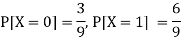
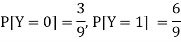
Now-
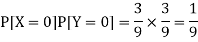
But

So that-
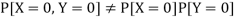
Hence X and Y are not independent.
Q5) A random variable x has the following probability distribution-
X | 0 | 1 | 2 | 3 | 4 | 5 |
p(x) | 0 | c | c | 2c | 3c | c |
Then find-
1. Value of c.
2. P[X≤3]
3. P[1 < X <4]
A5)
We know that for the given probability distribution-

So that-

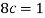

2.

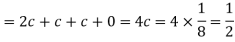
3.

Q6) In a lottery, m tickets are drawn at a time out of tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
A6)
Let  be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
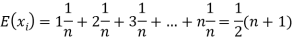
Therefore the expected value of the sum of the numbers on the tickets drawn

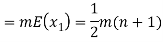
Q7) X is a continuous random variable with probability density function given by
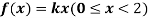


Find k and mean value of X.
A7)
Since the total probability is unity.

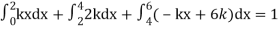
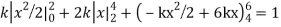
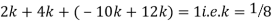
Mean of X =
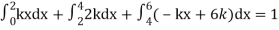
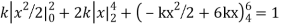



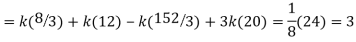
Q8) The frequency distribution of a measurable characteristic varying between 0 and 2 is as under


Calculate two standard deviations and also the mean deviation about the mean.
A8)
Total frequency N =
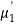 (about the origin)=
(about the origin)=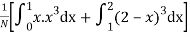
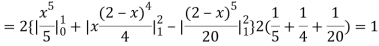
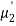 (about the origin)=
(about the origin)= 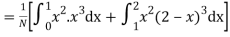
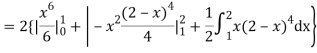
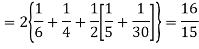
Hence, 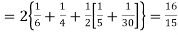
i.e., standard deviation 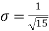
Mean derivation about the mean
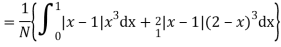
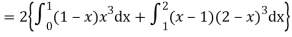
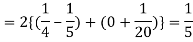
Q9) If a random variable X has the following probability distribution in the tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
A9)
We know that-

So that-

Q10) Find the expectations of the number of an unbiased die when thrown.
A10)
Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
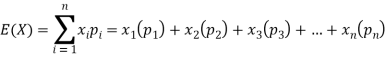
So that-
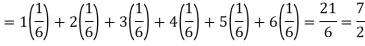
Q11) I roll a fair die and let X be the resulting number. Find E(X), Var(X), and 
A11)
We have  and
and 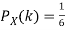 for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have
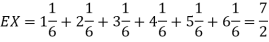
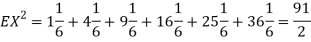
Thus,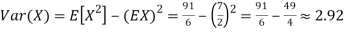
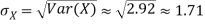
Q12) If on average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
A12)
Out of 10 ships, one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)
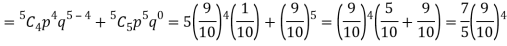
Q13) The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?
A13)
Probability of failures = 20% 
Probability of (P) = 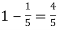
Probability of at least 5 passes = P(5 or 6)
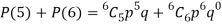
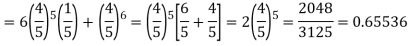
Q14) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?
A14)
The probability that a man aged 60 will live to be 70
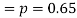

Number of men= n = 10
Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)
= P (7)+ P(8)+ P(9) + P(10) =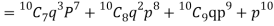

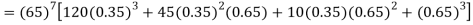
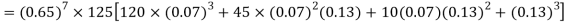
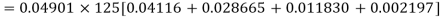
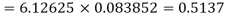
Q15) Find the mean and variance of a binomial distribution with p = 1/4 and n = 10.
A15)
Here 
Mean = np = 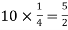
Variance = npq = 
Q16) Assume that the probability of an individual coal miner being killed in a mine accident during a year is 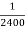 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
A16)
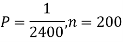
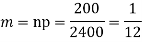
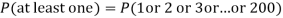

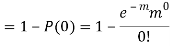
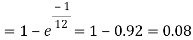
Q17) Suppose 3% of bolts made by a machine are defective, the defects occurring at random during production. If bolts are packaged 50 per box, find
(a) Exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
A17)
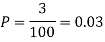
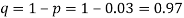
(a) Hence the probability for 5 defectives bolts in a lot of 50.
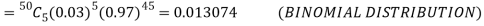
(b) To get Poisson approximation m = np =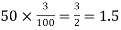
Required Poisson approximation=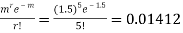
Q18) On a final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard scores of students receiving grades.
(a) 60
(b) 93
(c) 72
A18)
(a) 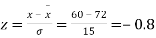
(b)
(c) 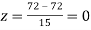
Q19) Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
A19)
(a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Q20) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise, the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.
A20)
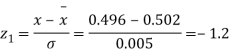
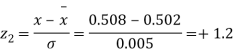
Area for non – defective washers = Area between z = -1.2
And z = +1.2
=2 Area between z = 0 and z = 1.2
=2 (0.3849)-0.7698=76.98%
(0.3849)-0.7698=76.98%
Percentage of defective washers = 100-76.98=23.02%
Q21) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 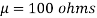 and standard deviation
and standard deviation 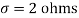 . What percentage of resistors will have resistance between 98 ohms and 102 ohms?
. What percentage of resistors will have resistance between 98 ohms and 102 ohms?
A21)
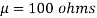 ,
,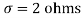
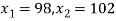
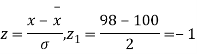

Area between 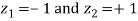
= (Area between z = 0 and z = +1)
= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826
0.3413 = 0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26
Q22) In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
A22)
Let 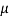 be the mean and
be the mean and  the S.D.
the S.D.
If x = 45, 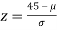
If x = 64, 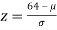
The area between 0 and 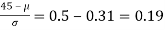
[From the table, for the area 0.19, z = 0.496)
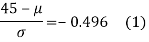
Area between z = 0 and z =
(from the table for area 0.42, z = 1.405)
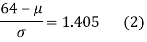
Solving (1) and (2) we get 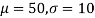
Q23) If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
A23)
The standard normal variate is –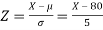
Now-
1. X = 95,
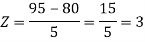
So that-
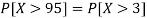
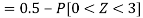

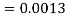

2. X = 72,
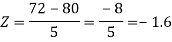
So that-
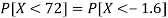
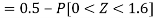

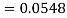

3. X = 85,
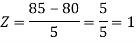
X = 97,

So that-
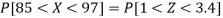


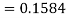

Q24) If a continuous random variable X has the following probability density function:
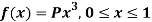
Then find-
1. P[0.2 < X < 0.5]
A24)
Here f(x) is the probability density function, then-
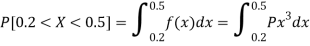
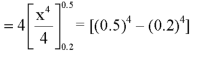
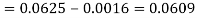
Q25) The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 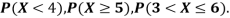
(ii) What will be e minimum value of k so that 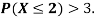
A25)
(i) If X is a random variable then
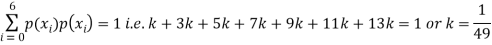
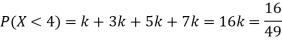
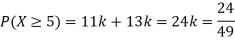
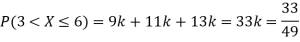
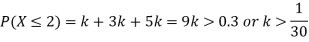
(ii)Thus minimum value of k=1/30.