Unit - 2
Vector Calculus
Q1) A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. Then find the velocity and acceleration at time t = 0 and t = π/2.
And find the magnitudes of the velocity and acceleration at time t.
A1)
Suppose 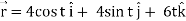
Now,
At t = 0 | 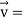 4 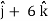 |
At t = π/2 | 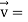 - 4  |
At t = 0 | |v|=  |
At t = π/2 | |v|= 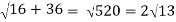 |
Again acceleration-
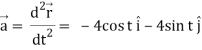
Now-
At t = 0 | 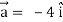 |
At t = π/2 | 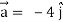 |
At t = 0 | |a|= (- 4 )2 = 4 |
At t = π/2 | |a|=(- 4 )2 = 4 |
Q2) Show that 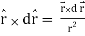 where
where 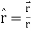
A2)
Here it is given-
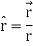
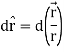
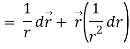
Therefore-
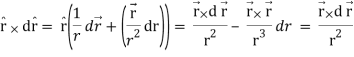
Note- 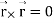
Hence proved.
Q3) Write the properties of gradient?
A3)
Properties of gradient-
Property-1:
(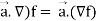
Proof:
First we will take left hand side
L.H.S = (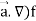
= ({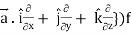
= ({
= 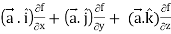
Now taking R.H.S,
R.H.S. =  (
(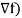
= 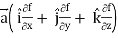
= 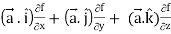
Here- L.H.S. = R.H.S.
Hence proved.
Property-2: Gradient of a constant (𝛁∅ = 0)
Proof:
Suppose ∅(x, y, z) = c
Then ∅/x = ∅/y = ∅/z = 0
We know that the gradient-


= 0
Property-3: Gradient of the sum and difference of two functions-
If f and g are two scalar point functions, then
∇(f ± g) = ∇f ± ∇g
Proof:
∇(f ± g) = 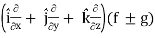
L.H.S
= 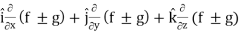
= 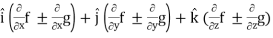
= 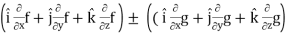
∇(f ± g) = ∇f ± ∇g
Hence proved
Property-4: Gradient of the product of two functions
If f and g are two scalar point functions, then
∇(fg) = f∇g + g∇f
Proof:
∇(fg) = 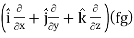
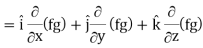
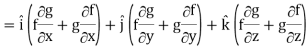
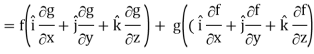
So that-
∇(fg) = f∇g + g∇f
Hence proved.
Property-5: Gradient of the quotient of two functions-
If f and g are two scalar point functions, then-
∇(f/g) = 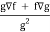
Proof:
∇(f/g) = 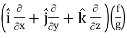
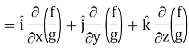
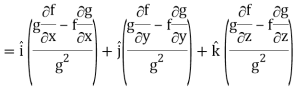
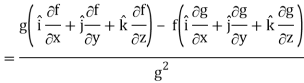
So that-
∇(f/g) = 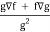
Q4) If 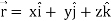 , then show that
, then show that
1. ∇(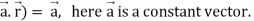
2. Grad r = 
A4)
Suppose 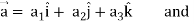
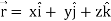
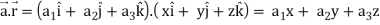
Now taking L.H.S,
∇(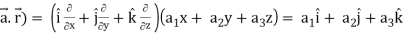
Which is 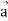
Hence proved.
2. Grad r = r = 
So that
Grad r = 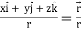
Q5) If f = 3x2y – y3z2 then find grad f at the point (1,-2,-1).
A5)
Grad f = 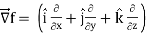 (3x2y – y3z2)
(3x2y – y3z2)
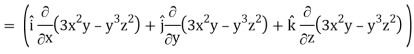
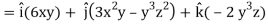
Now grad f at (1 , -2, -1) will be-
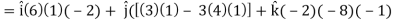
= - 12 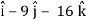
Q6) If u = x+ y+ z, v = x2 + y2 + z2 and w = yz + zx + xy then prove that grad u , grad v and grad w are coplanar.
A6)
Here- grad u = 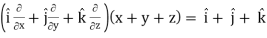
Grad v = 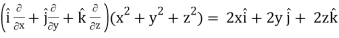
Grad w = 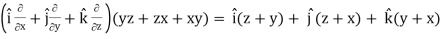
Now-
Grad u (grad v grad w) = 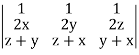
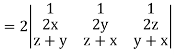
Apply R2 R2 + R3
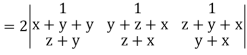
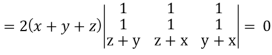
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Q7) What is Divergence and curl?
A7)
Divergence (Definition)-
Suppose 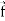 (x, y, z) is a given continuous differentiable vector function then the divergence of this function can be defined as-
(x, y, z) is a given continuous differentiable vector function then the divergence of this function can be defined as-
∇.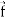 =
= 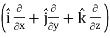 .
.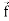 =
= 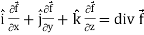
Curl (Definition)-
Curl of a vector function can be defined as-
Curl 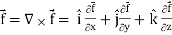
Note- Irrotational vector-
If curl 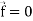 then the vector is said to be irrotational.
then the vector is said to be irrotational.
Q8) Write Vector identities.
A8)
Vector identities:
Identity-1: grad uv = u grad v + v grad u
Proof:
Grad (uv) = ∇ (uv)
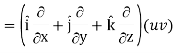
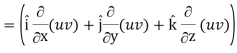
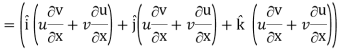
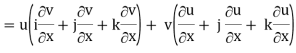
So that
Grad uv = u grad v + v grad u
Identity-2: grad(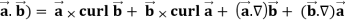 .
.
Proof:
Grad(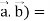
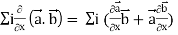
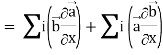
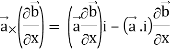
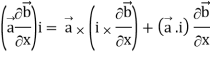
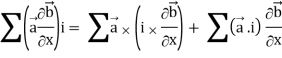
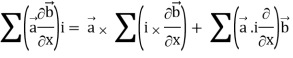
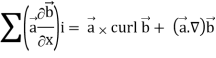
Interchanging 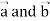 , we get-
, we get-
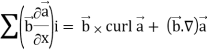
We get by using above equations-
Grad(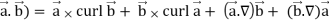
Identity-3 div (u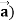 = u div
= u div 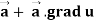
Proof: div  = ∇.(u
= ∇.(u 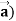
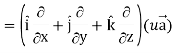
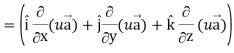
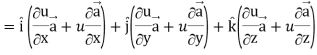
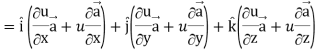
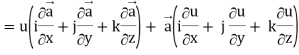
So that-
Div(u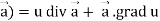
Identity-4 div (
Proof:
Div (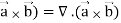
= 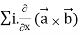
= 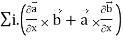
= 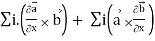
= 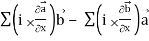
= ( curl  ) .
) .  - (curl
- (curl  ).
). 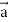
So that,
Div (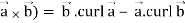
Identity-5 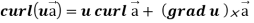
Proof:
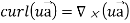
= 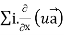
= 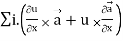
= 
= (grad u) 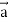 + u curl
+ u curl 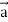
So that
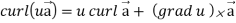
Identity-6: div curl 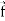 = 0
= 0
Proof:
Div curl 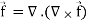

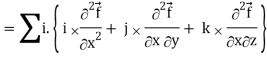
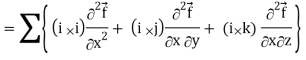
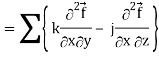
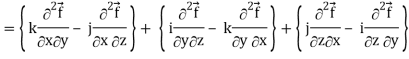
So that-
Div curl 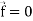
Identity-7: div grad f = ∇ . (∇f) = 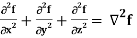
Proof:
Div grad f = ∇ . (∇f)
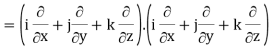
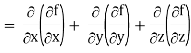
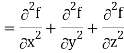
So that-
Divgrad f = ∇2 f
Q9) Show that-
1. Div 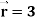
2. Curl 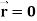
A9)
We know that-
Div 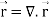
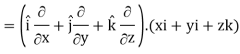
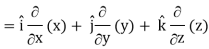
= 1 + 1 + 1 = 3
2. We know that
Curl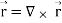

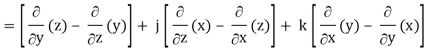
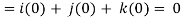
Q10) If 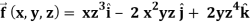 then find the divergence and curl of
then find the divergence and curl of  .
.
A10)
We know that-
Div 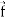 =
= 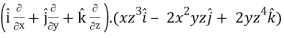
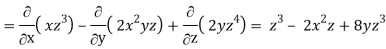
Now-
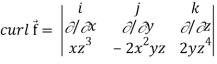

= I (2 z4 + 2x2y) – j (0 – 3z2x) + k(-4xyz – 0)
= 2 (x2y + z4) I + 3z2xj – 4 xyz.k
Q11) Prove that 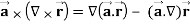
Note- here 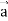 is a constant vector and
is a constant vector and 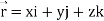
A11)
Here 
So that
∇ 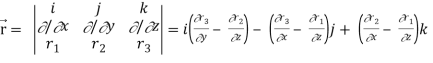
Now-
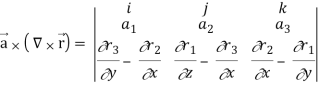
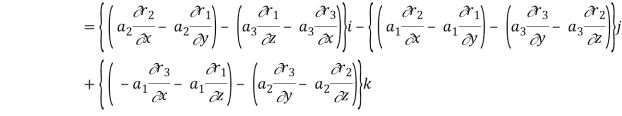
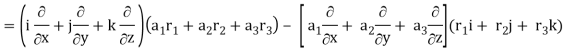
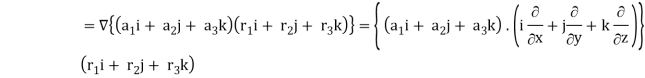
So that-
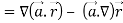
Q12) Evaluate 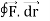 where F= cos y.i-x siny j and C is the curve y= 1 – x2 in the xy plane from (1,0) to (0,1)
where F= cos y.i-x siny j and C is the curve y= 1 – x2 in the xy plane from (1,0) to (0,1)
A12)
The curve y=1 – x2 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
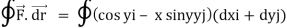
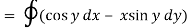
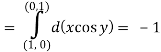
Q13) Evaluate 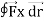 where
where 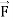 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A13)
F x dr = 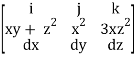
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr = 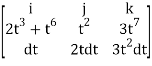
=(3t4-6t8) dt i – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=  t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
= [(3/5 -2/3)I + (1/1 + 1/3 – 3/8)j + (4/5 + 1/4 – 1/3)k]
= - 1/15 i + 23/24 j + 43/60 k
Q14) Evaluate 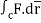 where
where 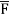 =yzi+zx j+xy k and C is the position of the curve.
=yzi+zx j+xy k and C is the position of the curve.
 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
A14)
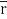 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)
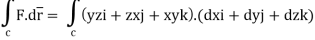

Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
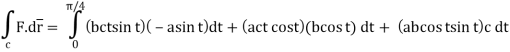
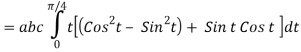
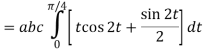
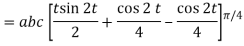
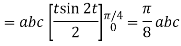
Q15) Evaluate 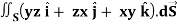 , where S is the surface of the sphere x2 + y2 + z2 = a2 in the first octant.
, where S is the surface of the sphere x2 + y2 + z2 = a2 in the first octant.
A15)
Here-
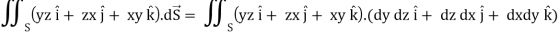
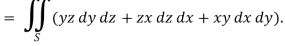

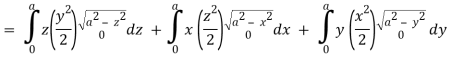
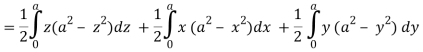

Which becomes-
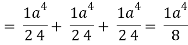
Q16) Evaluate  , where ∅ = 45 x2y and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
, where ∅ = 45 x2y and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
A16)
Here- 4x + 2y + z = 8
Put y = 0 and z = 0 in this, we get
4x = 8 or x = 2
Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x
And z varies from 0 to 8 – 4x – 2y
So that-
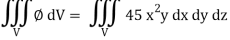
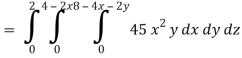
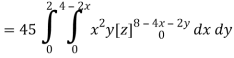
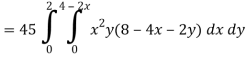
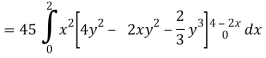
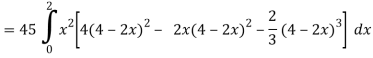
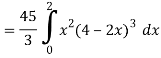
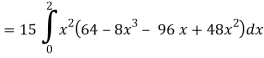
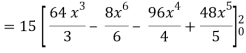
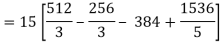
= 128
So that-
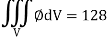
Q17) Evaluate 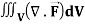 if V is the region in the first octant bounded by y2 + z2 = 9 and the plane x = 2 and
if V is the region in the first octant bounded by y2 + z2 = 9 and the plane x = 2 and 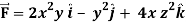 .
.
A17)

x varies from 0 to 2
The volume will be-


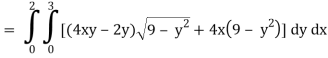
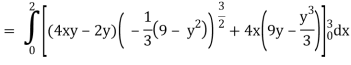
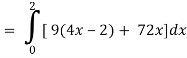
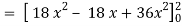
= 180
Q18) Apply Green’s theorem to evaluate 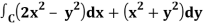 where C is the boundary of the area enclosed by the x-axis and the upper half of circle x2 + y2 = a2.
where C is the boundary of the area enclosed by the x-axis and the upper half of circle x2 + y2 = a2.
A18)
We know that by Green’s theorem-
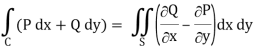
And it it given that-
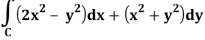
Now comparing the given integral-
P = 2x2 – y2 and Q = x2 + y2
Now-
Q/x = 2x and P/x = -2y
So that by Green’s theorem, we have the following integral-

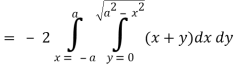
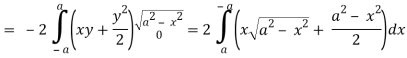
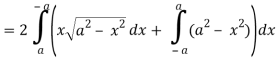

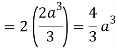
Q19) Evaluate 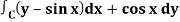 by using Green’s theorem, where C is a triangle formed by y = 0, x = π/2, y = 2x/π
by using Green’s theorem, where C is a triangle formed by y = 0, x = π/2, y = 2x/π
A19)
First we will draw the figure-

Here the vertices of triangle OED are (0,0), (π/2 , 0) and (π/2, π/2)
Now by using Green’s theorem-

Here P = y – sinx, and Q =cosx
So that-
Q/x = - sin x and P/x = 1
Now-
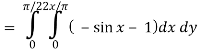
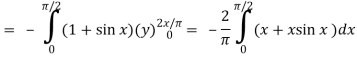

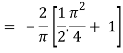

Which is the required answer.
Q20) Verify green’s theorem in xy-plane for  where C is the boundary of the region enclosed by y = x2 and y2 = x
where C is the boundary of the region enclosed by y = x2 and y2 = x
A20)
On comparing with green’s theorem,
We get-
P = 2xy – x2 and Q = x2 + y2
Q/x = 2x and P/x = 2x
By using Green’s theorem-

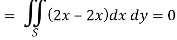
And left hand side = 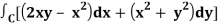
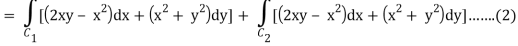
Now,
Along C1 : y = x2 that means dy = 2x dx where x varies from 0 to 1
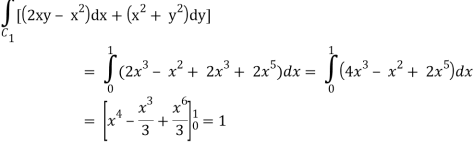
Along C2 : x2 = x that means 2ydy = dx or dy = dx/2x1/2 where x varies from 0 to
1
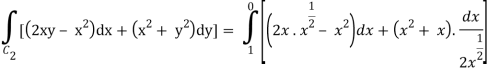
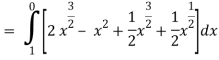
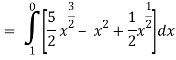
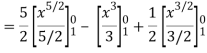

Put these values in (2), we get-
L.H.S. = 1 – 1 = 0
So that the Green’s theorem is verified.
Q21) Prove the following by using Gauss divergence theorem-
1. 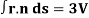
2. 
Where S is any closed surface having volume V and r2 = x2 + v2 + z2
A21)
Here we have by Gauss divergence theorem-

Where V is the volume enclose by the surface S.
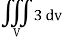
We know that-
Div r = 3
= 3V
2. 
Because 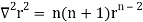

Q22) Show that 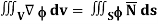
A22)
By divergence theorem,  ..…(1)
..…(1)
Comparing this with the given problem let

Hence, by (1)
 ………….(2)
………….(2)
Now, ∇ . 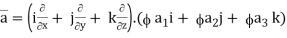
 ,
,
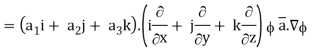
Hence, from (2), We get,
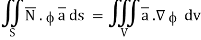
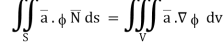
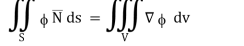
Q23) Show that

A23)
We have Gauss Divergence Theorem
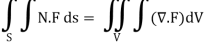
By data, F = rnr ∇.F = ∇.(rn. r)
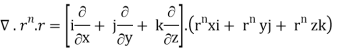
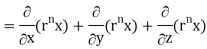
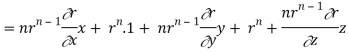
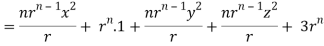
= nrn – 2 ( n2 + y2 + z2) + 3rn
= nrn – 2r2 + 3rn
∇. rn. r = nrn + 3rn
=(n+3)rn
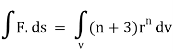
Q24) Prove that 
A24)
By Gauss Divergence Theorem,

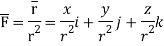
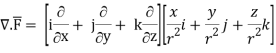
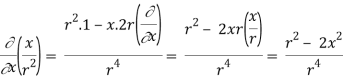
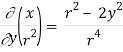
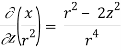
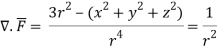
Q25) Verify stokes theorem when 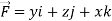 and surface S is the part of sphere x2 + y2 + z2 = 1 , above the xy-plane.
and surface S is the part of sphere x2 + y2 + z2 = 1 , above the xy-plane.
A25)
We know that by stoke’s theorem,
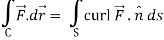
Here C is the unit circle-x2 + y2 = 1, z = 0
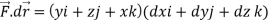

So that-
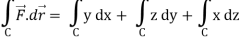
Now again on the unit circle C, z = 0
Dz = 0
Suppose, x = cos ∅ so that dx = - sin ∅. d∅
And y = sin ∅ so that dy = cos ∅. d∅
Now
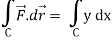

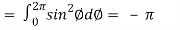 ……………… (1)
……………… (1)
Now-
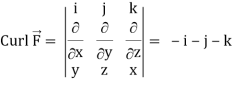
Using spherical polar coordinates-
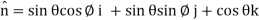
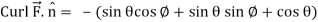
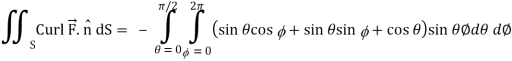

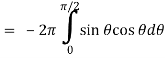
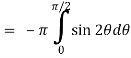
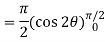
= - π ………………… (2)
From equation (1) and (2), stokes theorem is verified.
Q26) If 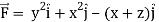 and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate 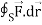 by using Stoke’s theorem.
by using Stoke’s theorem.
A26)
Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 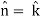
Now,
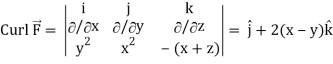
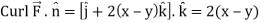

The equation of the line OB is y = x
Now by stokes theorem,
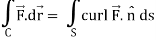
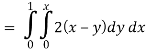

Q27) Verify Stoke’s theorem for the given function-
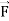 = (x+2y) dx + (y + 3x) dy
= (x+2y) dx + (y + 3x) dy
Where C is the unit circle in the xy-plane.
A27)
Suppose-
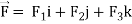
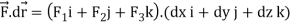
= F1dx + F2 dy + F3 dz
Here F1 = x+2y, F2 = y+ 3x, F3 = 0
We know that unit circle in xy-plane-
Or
x = cos ∅, dx = - sin ∅ d∅
y = sin ∅, dy = cos ∅ d∅
So that,
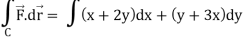
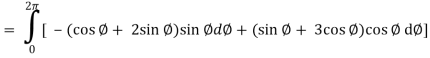
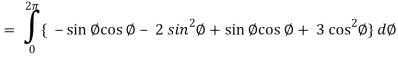
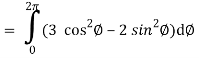

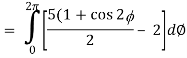
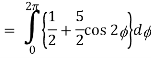
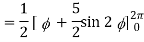
= ½ [ 2π + 0] = π
Now
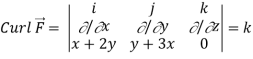
Now,
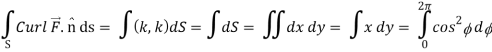
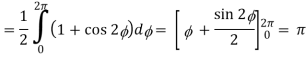
Hence the Stokes theorem is verified.
Unit - 2
Vector Calculus
Q1) A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. Then find the velocity and acceleration at time t = 0 and t = π/2.
And find the magnitudes of the velocity and acceleration at time t.
A1)
Suppose 
Now,
At t = 0 |  4 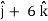 |
At t = π/2 |  - 4  |
At t = 0 | |v|= 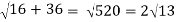 |
At t = π/2 | |v|= 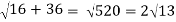 |
Again acceleration-
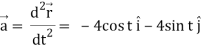
Now-
At t = 0 | 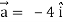 |
At t = π/2 | 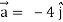 |
At t = 0 | |a|= (- 4 )2 = 4 |
At t = π/2 | |a|=(- 4 )2 = 4 |
Q2) Show that 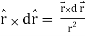 where
where 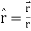
A2)
Here it is given-
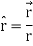
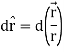
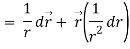
Therefore-
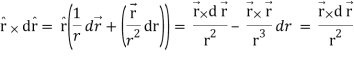
Note- 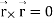
Hence proved.
Q3) Write the properties of gradient?
A3)
Properties of gradient-
Property-1:
(
Proof:
First we will take left hand side
L.H.S = (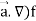
= ({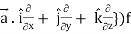
= ({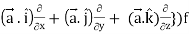
= 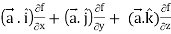
Now taking R.H.S,
R.H.S. = 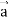 (
(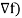
= 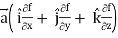
= 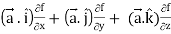
Here- L.H.S. = R.H.S.
Hence proved.
Property-2: Gradient of a constant (𝛁∅ = 0)
Proof:
Suppose ∅(x, y, z) = c
Then ∅/x = ∅/y = ∅/z = 0
We know that the gradient-
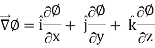

= 0
Property-3: Gradient of the sum and difference of two functions-
If f and g are two scalar point functions, then
∇(f ± g) = ∇f ± ∇g
Proof:
∇(f ± g) = 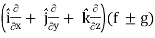
L.H.S
= 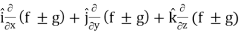
= 
= 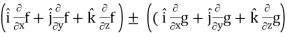
∇(f ± g) = ∇f ± ∇g
Hence proved
Property-4: Gradient of the product of two functions
If f and g are two scalar point functions, then
∇(fg) = f∇g + g∇f
Proof:
∇(fg) = 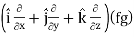
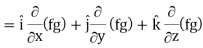
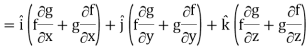
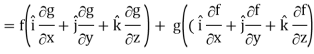
So that-
∇(fg) = f∇g + g∇f
Hence proved.
Property-5: Gradient of the quotient of two functions-
If f and g are two scalar point functions, then-
∇(f/g) = 
Proof:
∇(f/g) = 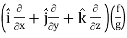

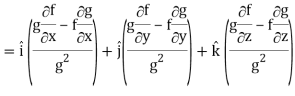
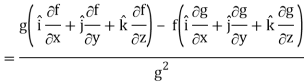
So that-
∇(f/g) = 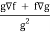
Q4) If 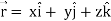 , then show that
, then show that
1. ∇(
2. Grad r = 
A4)
Suppose 
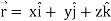
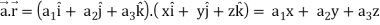
Now taking L.H.S,
∇(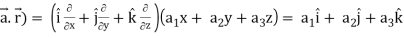
Which is 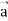
Hence proved.
2. Grad r = r = 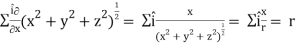
So that
Grad r = 
Q5) If f = 3x2y – y3z2 then find grad f at the point (1,-2,-1).
A5)
Grad f = 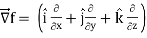 (3x2y – y3z2)
(3x2y – y3z2)
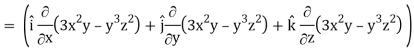
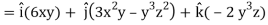
Now grad f at (1 , -2, -1) will be-
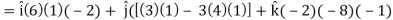
= - 12 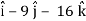
Q6) If u = x+ y+ z, v = x2 + y2 + z2 and w = yz + zx + xy then prove that grad u , grad v and grad w are coplanar.
A6)
Here- grad u = 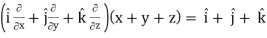
Grad v = 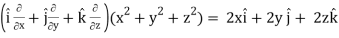
Grad w = 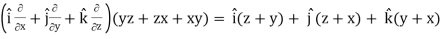
Now-
Grad u (grad v grad w) = 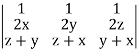

Apply R2 R2 + R3
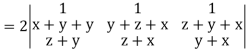
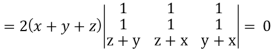
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Q7) What is Divergence and curl?
A7)
Divergence (Definition)-
Suppose  (x, y, z) is a given continuous differentiable vector function then the divergence of this function can be defined as-
(x, y, z) is a given continuous differentiable vector function then the divergence of this function can be defined as-
∇.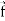 =
= 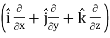 .
.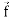 =
= 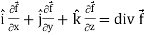
Curl (Definition)-
Curl of a vector function can be defined as-
Curl 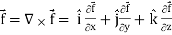
Note- Irrotational vector-
If curl 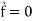 then the vector is said to be irrotational.
then the vector is said to be irrotational.
Q8) Write Vector identities.
A8)
Vector identities:
Identity-1: grad uv = u grad v + v grad u
Proof:
Grad (uv) = ∇ (uv)
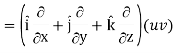
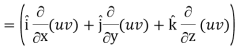

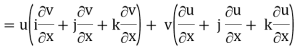
So that
Grad uv = u grad v + v grad u
Identity-2: grad(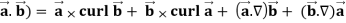 .
.
Proof:
Grad(
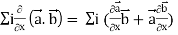

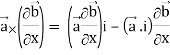
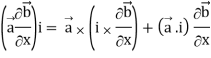
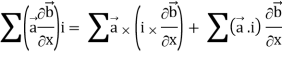
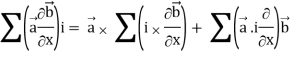
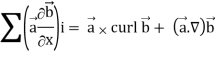
Interchanging 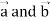 , we get-
, we get-

We get by using above equations-
Grad(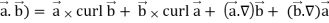
Identity-3 div (u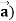 = u div
= u div 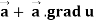
Proof: div 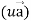 = ∇.(u
= ∇.(u 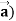
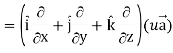
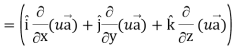
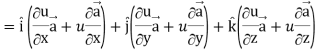
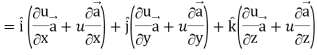
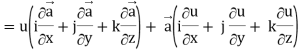
So that-
Div(u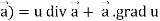
Identity-4 div (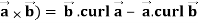
Proof:
Div (
= 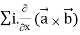
= 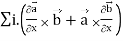
= 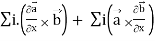
= 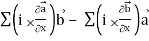
= ( curl 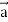 ) .
) . 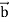 - (curl
- (curl 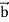 ).
). 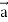
So that,
Div (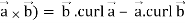
Identity-5 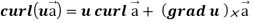
Proof:
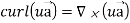
= 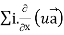
= 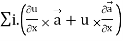
= 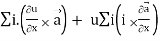
= (grad u)  + u curl
+ u curl 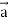
So that
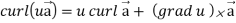
Identity-6: div curl  = 0
= 0
Proof:
Div curl 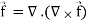
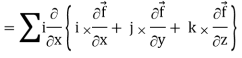
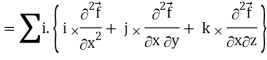
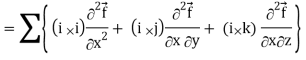
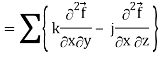
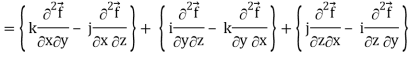
So that-
Div curl 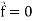
Identity-7: div grad f = ∇ . (∇f) = 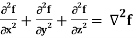
Proof:
Div grad f = ∇ . (∇f)

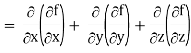
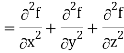
So that-
Divgrad f = ∇2 f
Q9) Show that-
1. Div 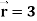
2. Curl 
A9)
We know that-
Div 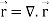
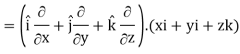
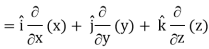
= 1 + 1 + 1 = 3
2. We know that
Curl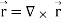
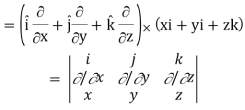
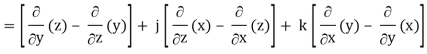
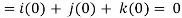
Q10) If 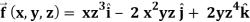 then find the divergence and curl of
then find the divergence and curl of 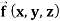 .
.
A10)
We know that-
Div 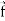 =
= 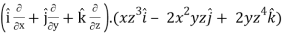
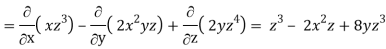
Now-
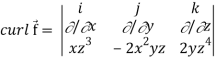

= I (2 z4 + 2x2y) – j (0 – 3z2x) + k(-4xyz – 0)
= 2 (x2y + z4) I + 3z2xj – 4 xyz.k
Q11) Prove that 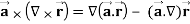
Note- here 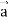 is a constant vector and
is a constant vector and 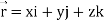
A11)
Here 
So that
∇ 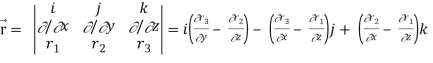
Now-
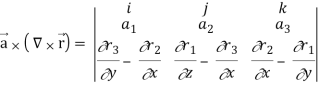
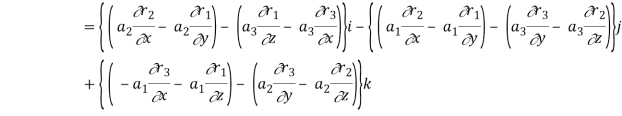
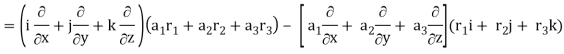
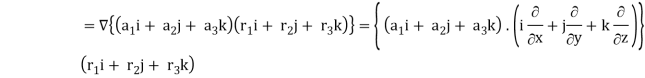
So that-
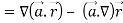
Q12) Evaluate 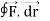 where F= cos y.i-x siny j and C is the curve y= 1 – x2 in the xy plane from (1,0) to (0,1)
where F= cos y.i-x siny j and C is the curve y= 1 – x2 in the xy plane from (1,0) to (0,1)
A12)
The curve y=1 – x2 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
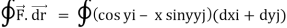
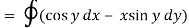
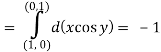
Q13) Evaluate 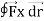 where
where  = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A13)
F x dr = 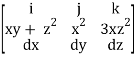
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr = 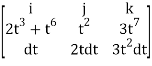
=(3t4-6t8) dt i – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
= 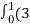 t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
= [(3/5 -2/3)I + (1/1 + 1/3 – 3/8)j + (4/5 + 1/4 – 1/3)k]
= - 1/15 i + 23/24 j + 43/60 k
Q14) Evaluate 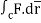 where
where 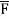 =yzi+zx j+xy k and C is the position of the curve.
=yzi+zx j+xy k and C is the position of the curve.
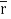 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
A14)
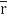 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)
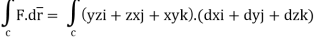

Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
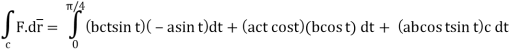
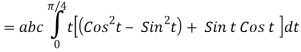
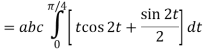
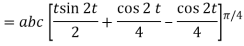
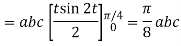
Q15) Evaluate  , where S is the surface of the sphere x2 + y2 + z2 = a2 in the first octant.
, where S is the surface of the sphere x2 + y2 + z2 = a2 in the first octant.
A15)
Here-


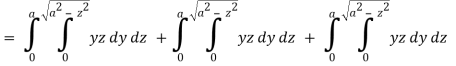
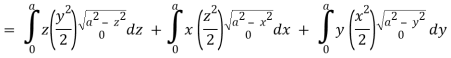
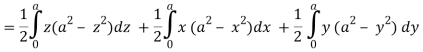
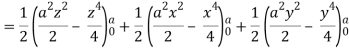
Which becomes-
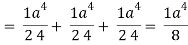
Q16) Evaluate  , where ∅ = 45 x2y and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
, where ∅ = 45 x2y and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
A16)
Here- 4x + 2y + z = 8
Put y = 0 and z = 0 in this, we get
4x = 8 or x = 2
Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x
And z varies from 0 to 8 – 4x – 2y
So that-
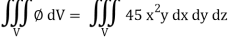
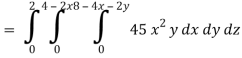
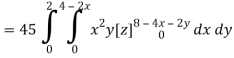
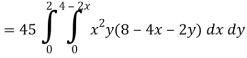
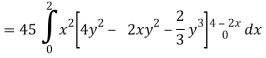
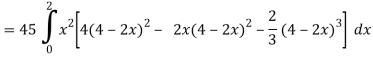
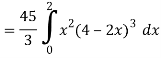
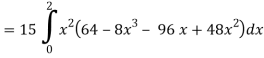
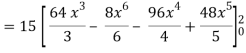
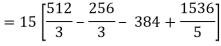
= 128
So that-
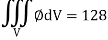
Q17) Evaluate 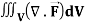 if V is the region in the first octant bounded by y2 + z2 = 9 and the plane x = 2 and
if V is the region in the first octant bounded by y2 + z2 = 9 and the plane x = 2 and  .
.
A17)
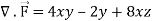
x varies from 0 to 2
The volume will be-
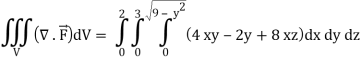
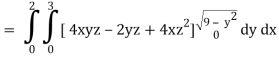
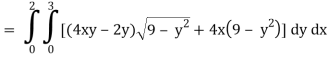

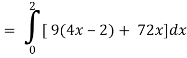
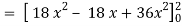
= 180
Q18) Apply Green’s theorem to evaluate  where C is the boundary of the area enclosed by the x-axis and the upper half of circle x2 + y2 = a2.
where C is the boundary of the area enclosed by the x-axis and the upper half of circle x2 + y2 = a2.
A18)
We know that by Green’s theorem-
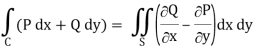
And it it given that-
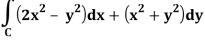
Now comparing the given integral-
P = 2x2 – y2 and Q = x2 + y2
Now-
Q/x = 2x and P/x = -2y
So that by Green’s theorem, we have the following integral-
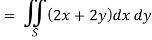


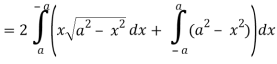
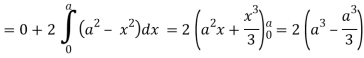

Q19) Evaluate 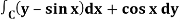 by using Green’s theorem, where C is a triangle formed by y = 0, x = π/2, y = 2x/π
by using Green’s theorem, where C is a triangle formed by y = 0, x = π/2, y = 2x/π
A19)
First we will draw the figure-
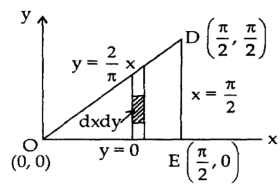
Here the vertices of triangle OED are (0,0), (π/2 , 0) and (π/2, π/2)
Now by using Green’s theorem-
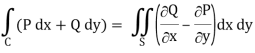
Here P = y – sinx, and Q =cosx
So that-
Q/x = - sin x and P/x = 1
Now-
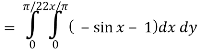
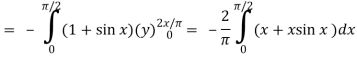
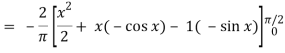
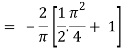

Which is the required answer.
Q20) Verify green’s theorem in xy-plane for 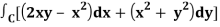 where C is the boundary of the region enclosed by y = x2 and y2 = x
where C is the boundary of the region enclosed by y = x2 and y2 = x
A20)
On comparing with green’s theorem,
We get-
P = 2xy – x2 and Q = x2 + y2
Q/x = 2x and P/x = 2x
By using Green’s theorem-
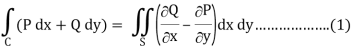
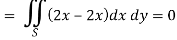
And left hand side = 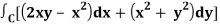
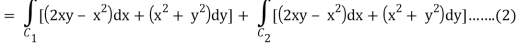
Now,
Along C1 : y = x2 that means dy = 2x dx where x varies from 0 to 1

Along C2 : x2 = x that means 2ydy = dx or dy = dx/2x1/2 where x varies from 0 to
1

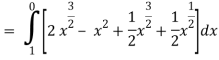
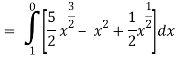
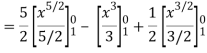
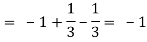
Put these values in (2), we get-
L.H.S. = 1 – 1 = 0
So that the Green’s theorem is verified.
Q21) Prove the following by using Gauss divergence theorem-
1. 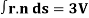
2. 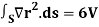
Where S is any closed surface having volume V and r2 = x2 + v2 + z2
A21)
Here we have by Gauss divergence theorem-
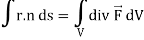
Where V is the volume enclose by the surface S.

We know that-
Div r = 3
= 3V
2. 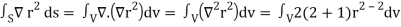
Because 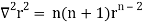

Q22) Show that 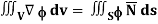
A22)
By divergence theorem, 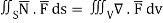 ..…(1)
..…(1)
Comparing this with the given problem let
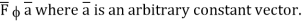
Hence, by (1)
 ………….(2)
………….(2)
Now, ∇ . 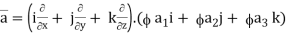
 ,
,
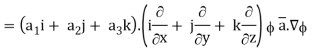
Hence, from (2), We get,
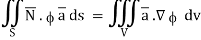

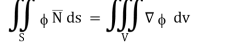
Q23) Show that

A23)
We have Gauss Divergence Theorem
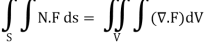
By data, F = rnr ∇.F = ∇.(rn. r)
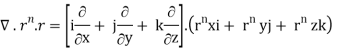
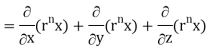
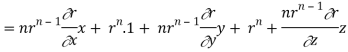
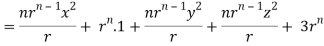
= nrn – 2 ( n2 + y2 + z2) + 3rn
= nrn – 2r2 + 3rn
∇. rn. r = nrn + 3rn
=(n+3)rn
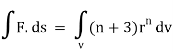
Q24) Prove that 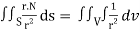
A24)
By Gauss Divergence Theorem,
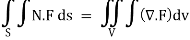

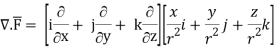
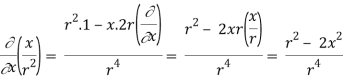
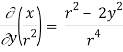
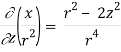

Q25) Verify stokes theorem when 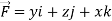 and surface S is the part of sphere x2 + y2 + z2 = 1 , above the xy-plane.
and surface S is the part of sphere x2 + y2 + z2 = 1 , above the xy-plane.
A25)
We know that by stoke’s theorem,
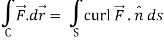
Here C is the unit circle-x2 + y2 = 1, z = 0
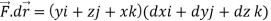

So that-
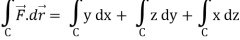
Now again on the unit circle C, z = 0
Dz = 0
Suppose, x = cos ∅ so that dx = - sin ∅. d∅
And y = sin ∅ so that dy = cos ∅. d∅
Now
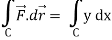

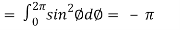 ……………… (1)
……………… (1)
Now-
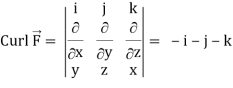
Using spherical polar coordinates-
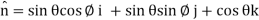
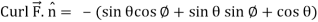
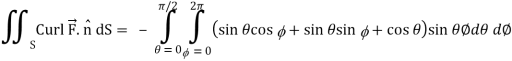
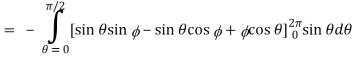
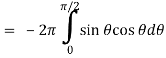
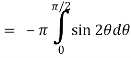
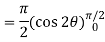
= - π ………………… (2)
From equation (1) and (2), stokes theorem is verified.
Q26) If 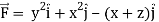 and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate 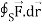 by using Stoke’s theorem.
by using Stoke’s theorem.
A26)
Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 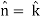
Now,
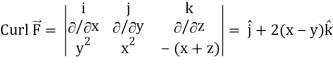
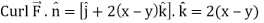
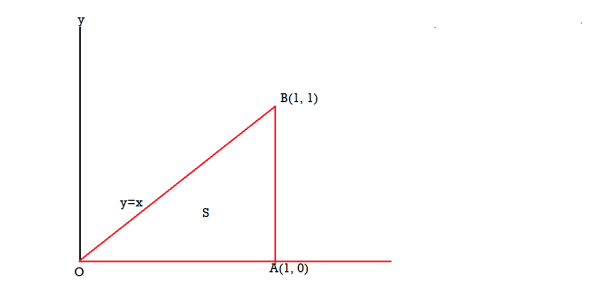
The equation of the line OB is y = x
Now by stokes theorem,
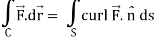
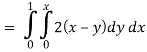
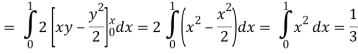
Q27) Verify Stoke’s theorem for the given function-
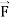 = (x+2y) dx + (y + 3x) dy
= (x+2y) dx + (y + 3x) dy
Where C is the unit circle in the xy-plane.
A27)
Suppose-
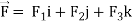
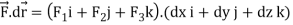
= F1dx + F2 dy + F3 dz
Here F1 = x+2y, F2 = y+ 3x, F3 = 0
We know that unit circle in xy-plane-
Or
x = cos ∅, dx = - sin ∅ d∅
y = sin ∅, dy = cos ∅ d∅
So that,


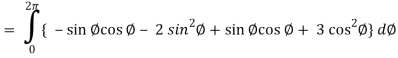
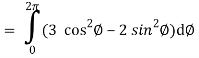
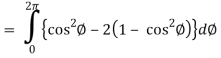
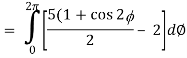
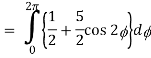
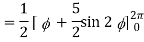
= ½ [ 2π + 0] = π
Now
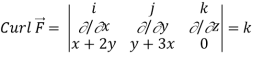
Now,
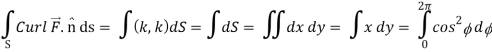
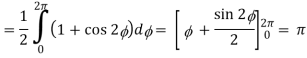
Hence the Stokes theorem is verified.
Unit - 2
Unit - 2
Unit - 2
Unit - 2
Unit - 2
Vector Calculus
Q1) A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. Then find the velocity and acceleration at time t = 0 and t = π/2.
And find the magnitudes of the velocity and acceleration at time t.
A1)
Suppose 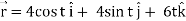
Now,
At t = 0 | 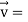 4 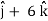 |
At t = π/2 | 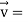 - 4 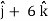 |
At t = 0 | |v|= 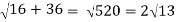 |
At t = π/2 | |v|= 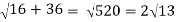 |
Again acceleration-
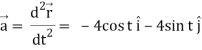
Now-
At t = 0 | 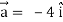 |
At t = π/2 | 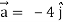 |
At t = 0 | |a|= (- 4 )2 = 4 |
At t = π/2 | |a|=(- 4 )2 = 4 |
Q2) Show that 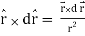 where
where 
A2)
Here it is given-

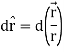
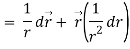
Therefore-
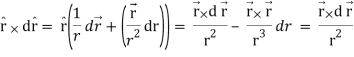
Note- 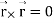
Hence proved.
Q3) Write the properties of gradient?
A3)
Properties of gradient-
Property-1:
(
Proof:
First we will take left hand side
L.H.S = (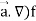
= ({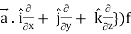
= ({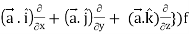
= 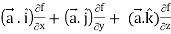
Now taking R.H.S,
R.H.S. = 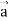 (
(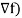
= 
= 
Here- L.H.S. = R.H.S.
Hence proved.
Property-2: Gradient of a constant (𝛁∅ = 0)
Proof:
Suppose ∅(x, y, z) = c
Then ∅/x = ∅/y = ∅/z = 0
We know that the gradient-
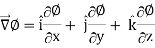
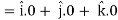
= 0
Property-3: Gradient of the sum and difference of two functions-
If f and g are two scalar point functions, then
∇(f ± g) = ∇f ± ∇g
Proof:
∇(f ± g) = 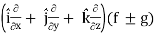
L.H.S
= 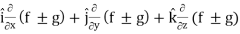
= 
= 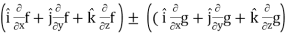
∇(f ± g) = ∇f ± ∇g
Hence proved
Property-4: Gradient of the product of two functions
If f and g are two scalar point functions, then
∇(fg) = f∇g + g∇f
Proof:
∇(fg) = 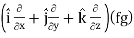
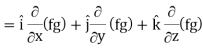
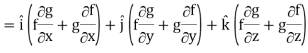
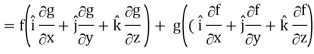
So that-
∇(fg) = f∇g + g∇f
Hence proved.
Property-5: Gradient of the quotient of two functions-
If f and g are two scalar point functions, then-
∇(f/g) = 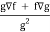
Proof:
∇(f/g) = 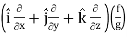
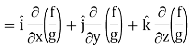
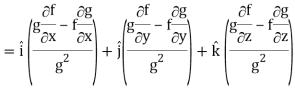
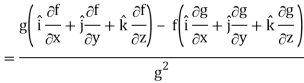
So that-
∇(f/g) = 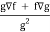
Q4) If 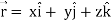 , then show that
, then show that
1. ∇(
2. Grad r = 
A4)
Suppose 

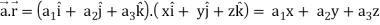
Now taking L.H.S,
∇(
Which is 
Hence proved.
2. Grad r = r = 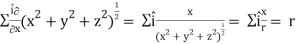
So that
Grad r = 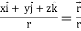
Q5) If f = 3x2y – y3z2 then find grad f at the point (1,-2,-1).
A5)
Grad f = 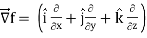 (3x2y – y3z2)
(3x2y – y3z2)


Now grad f at (1 , -2, -1) will be-
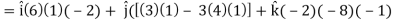
= - 12 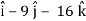
Q6) If u = x+ y+ z, v = x2 + y2 + z2 and w = yz + zx + xy then prove that grad u , grad v and grad w are coplanar.
A6)
Here- grad u = 
Grad v = 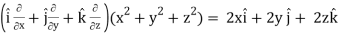
Grad w = 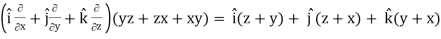
Now-
Grad u (grad v grad w) = 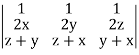
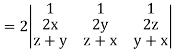
Apply R2 R2 + R3
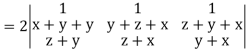
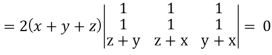
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Q7) What is Divergence and curl?
A7)
Divergence (Definition)-
Suppose 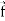 (x, y, z) is a given continuous differentiable vector function then the divergence of this function can be defined as-
(x, y, z) is a given continuous differentiable vector function then the divergence of this function can be defined as-
∇.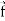 =
= 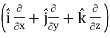 .
.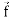 =
= 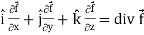
Curl (Definition)-
Curl of a vector function can be defined as-
Curl 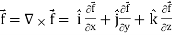
Note- Irrotational vector-
If curl  then the vector is said to be irrotational.
then the vector is said to be irrotational.
Q8) Write Vector identities.
A8)
Vector identities:
Identity-1: grad uv = u grad v + v grad u
Proof:
Grad (uv) = ∇ (uv)
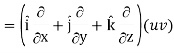

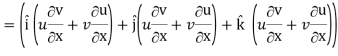
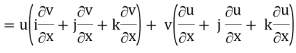
So that
Grad uv = u grad v + v grad u
Identity-2: grad( .
.
Proof:
Grad(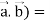
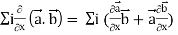
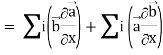
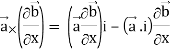
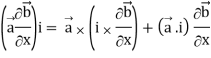


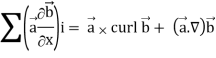
Interchanging 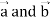 , we get-
, we get-
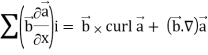
We get by using above equations-
Grad(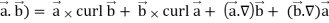
Identity-3 div (u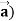 = u div
= u div 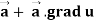
Proof: div  = ∇.(u
= ∇.(u 

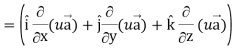
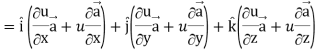

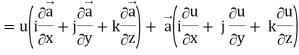
So that-
Div(u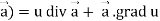
Identity-4 div (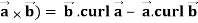
Proof:
Div (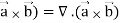
= 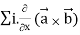
= 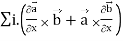
= 
= 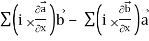
= ( curl  ) .
) . 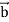 - (curl
- (curl 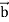 ).
). 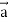
So that,
Div (
Identity-5 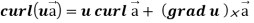
Proof:

= 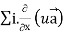
= 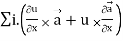
= 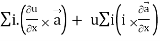
= (grad u) 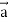 + u curl
+ u curl 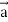
So that
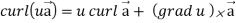
Identity-6: div curl 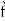 = 0
= 0
Proof:
Div curl 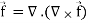
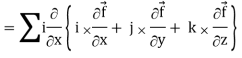
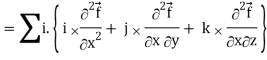

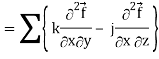
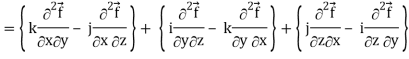
So that-
Div curl 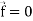
Identity-7: div grad f = ∇ . (∇f) = 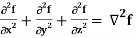
Proof:
Div grad f = ∇ . (∇f)
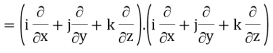

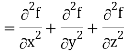
So that-
Divgrad f = ∇2 f
Q9) Show that-
1. Div 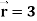
2. Curl 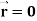
A9)
We know that-
Div 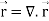
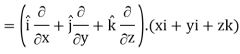

= 1 + 1 + 1 = 3
2. We know that
Curl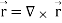
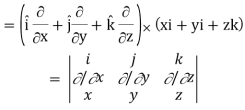
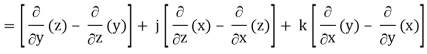
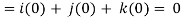
Q10) If  then find the divergence and curl of
then find the divergence and curl of 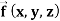 .
.
A10)
We know that-
Div 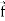 =
= 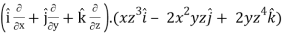

Now-
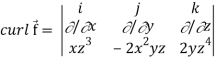
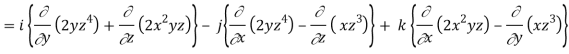
= I (2 z4 + 2x2y) – j (0 – 3z2x) + k(-4xyz – 0)
= 2 (x2y + z4) I + 3z2xj – 4 xyz.k
Q11) Prove that 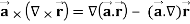
Note- here 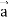 is a constant vector and
is a constant vector and 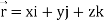
A11)
Here 
So that
∇ 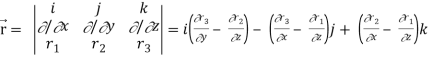
Now-
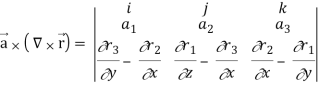

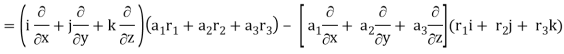
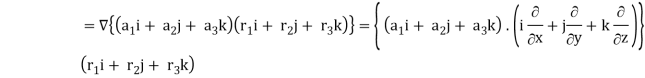
So that-
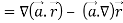
Q12) Evaluate 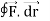 where F= cos y.i-x siny j and C is the curve y= 1 – x2 in the xy plane from (1,0) to (0,1)
where F= cos y.i-x siny j and C is the curve y= 1 – x2 in the xy plane from (1,0) to (0,1)
A12)
The curve y=1 – x2 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
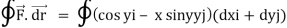
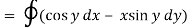
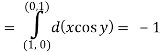
Q13) Evaluate 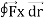 where
where 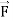 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A13)
F x dr = 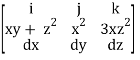
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr = 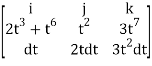
=(3t4-6t8) dt i – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=  t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
= [(3/5 -2/3)I + (1/1 + 1/3 – 3/8)j + (4/5 + 1/4 – 1/3)k]
= - 1/15 i + 23/24 j + 43/60 k
Q14) Evaluate 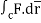 where
where 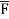 =yzi+zx j+xy k and C is the position of the curve.
=yzi+zx j+xy k and C is the position of the curve.
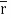 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
A14)
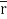 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)
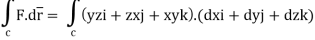
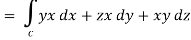
Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
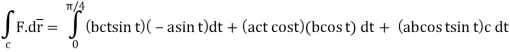

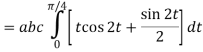
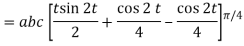
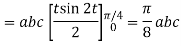
Q15) Evaluate 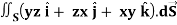 , where S is the surface of the sphere x2 + y2 + z2 = a2 in the first octant.
, where S is the surface of the sphere x2 + y2 + z2 = a2 in the first octant.
A15)
Here-
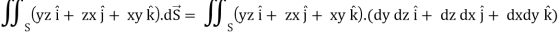
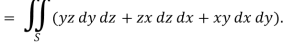
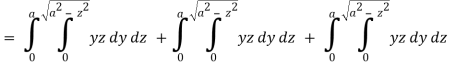
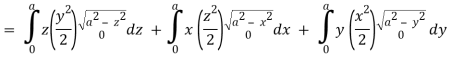
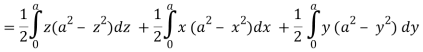
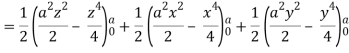
Which becomes-
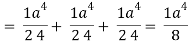
Q16) Evaluate 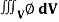 , where ∅ = 45 x2y and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
, where ∅ = 45 x2y and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
A16)
Here- 4x + 2y + z = 8
Put y = 0 and z = 0 in this, we get
4x = 8 or x = 2
Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x
And z varies from 0 to 8 – 4x – 2y
So that-
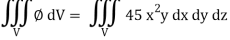
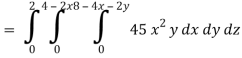

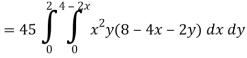
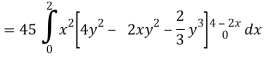
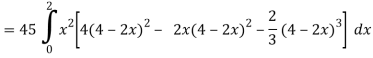
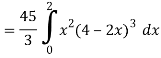
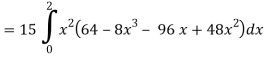
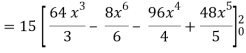
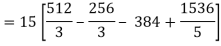
= 128
So that-
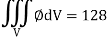
Q17) Evaluate  if V is the region in the first octant bounded by y2 + z2 = 9 and the plane x = 2 and
if V is the region in the first octant bounded by y2 + z2 = 9 and the plane x = 2 and 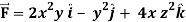 .
.
A17)
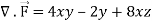
x varies from 0 to 2
The volume will be-
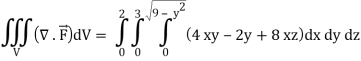
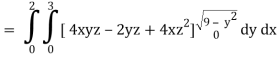
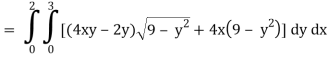
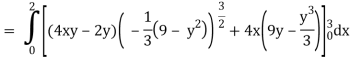
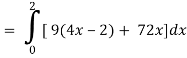
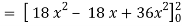
= 180
Q18) Apply Green’s theorem to evaluate 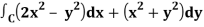 where C is the boundary of the area enclosed by the x-axis and the upper half of circle x2 + y2 = a2.
where C is the boundary of the area enclosed by the x-axis and the upper half of circle x2 + y2 = a2.
A18)
We know that by Green’s theorem-

And it it given that-

Now comparing the given integral-
P = 2x2 – y2 and Q = x2 + y2
Now-
Q/x = 2x and P/x = -2y
So that by Green’s theorem, we have the following integral-
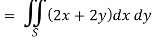
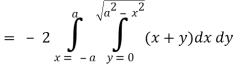
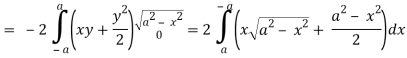
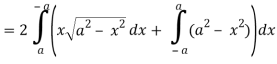
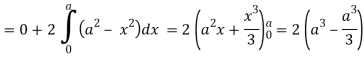
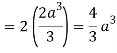
Q19) Evaluate 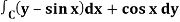 by using Green’s theorem, where C is a triangle formed by y = 0, x = π/2, y = 2x/π
by using Green’s theorem, where C is a triangle formed by y = 0, x = π/2, y = 2x/π
A19)
First we will draw the figure-
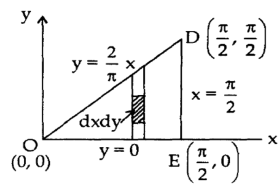
Here the vertices of triangle OED are (0,0), (π/2 , 0) and (π/2, π/2)
Now by using Green’s theorem-
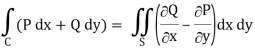
Here P = y – sinx, and Q =cosx
So that-
Q/x = - sin x and P/x = 1
Now-
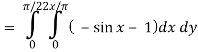
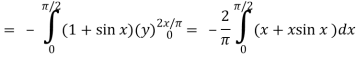

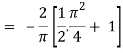

Which is the required answer.
Q20) Verify green’s theorem in xy-plane for 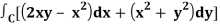 where C is the boundary of the region enclosed by y = x2 and y2 = x
where C is the boundary of the region enclosed by y = x2 and y2 = x
A20)
On comparing with green’s theorem,
We get-
P = 2xy – x2 and Q = x2 + y2
Q/x = 2x and P/x = 2x
By using Green’s theorem-
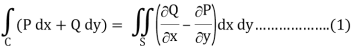
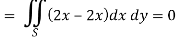
And left hand side = 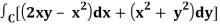

Now,
Along C1 : y = x2 that means dy = 2x dx where x varies from 0 to 1
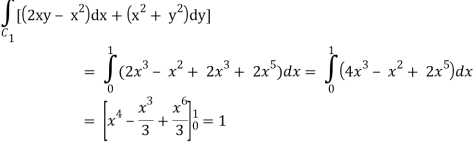
Along C2 : x2 = x that means 2ydy = dx or dy = dx/2x1/2 where x varies from 0 to
1
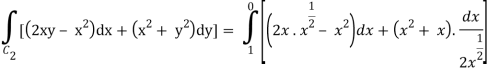
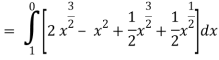
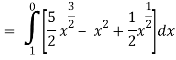
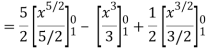

Put these values in (2), we get-
L.H.S. = 1 – 1 = 0
So that the Green’s theorem is verified.
Q21) Prove the following by using Gauss divergence theorem-
1. 
2. 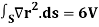
Where S is any closed surface having volume V and r2 = x2 + v2 + z2
A21)
Here we have by Gauss divergence theorem-
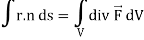
Where V is the volume enclose by the surface S.
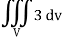
We know that-
Div r = 3
= 3V
2. 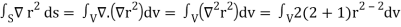
Because 
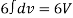
Q22) Show that 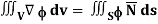
A22)
By divergence theorem, 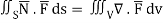 ..…(1)
..…(1)
Comparing this with the given problem let

Hence, by (1)
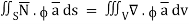 ………….(2)
………….(2)
Now, ∇ . 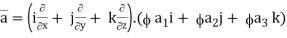
 ,
,

Hence, from (2), We get,
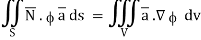

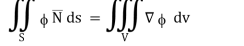
Q23) Show that

A23)
We have Gauss Divergence Theorem
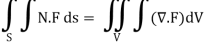
By data, F = rnr ∇.F = ∇.(rn. r)
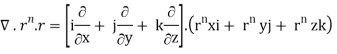
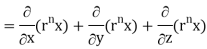
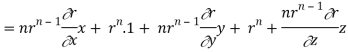
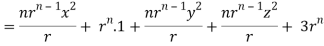
= nrn – 2 ( n2 + y2 + z2) + 3rn
= nrn – 2r2 + 3rn
∇. rn. r = nrn + 3rn
=(n+3)rn

Q24) Prove that 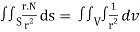
A24)
By Gauss Divergence Theorem,
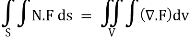
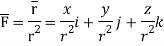


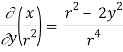

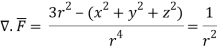
Q25) Verify stokes theorem when  and surface S is the part of sphere x2 + y2 + z2 = 1 , above the xy-plane.
and surface S is the part of sphere x2 + y2 + z2 = 1 , above the xy-plane.
A25)
We know that by stoke’s theorem,
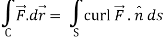
Here C is the unit circle-x2 + y2 = 1, z = 0
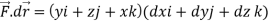
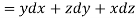
So that-
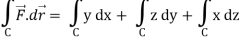
Now again on the unit circle C, z = 0
Dz = 0
Suppose, x = cos ∅ so that dx = - sin ∅. d∅
And y = sin ∅ so that dy = cos ∅. d∅
Now
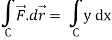
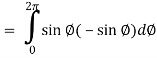
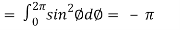 ……………… (1)
……………… (1)
Now-
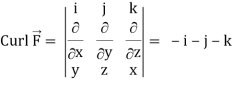
Using spherical polar coordinates-
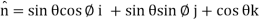
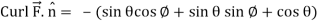
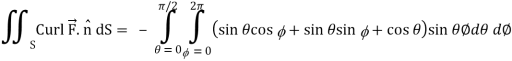
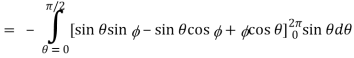


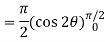
= - π ………………… (2)
From equation (1) and (2), stokes theorem is verified.
Q26) If 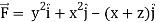 and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate  by using Stoke’s theorem.
by using Stoke’s theorem.
A26)
Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 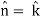
Now,
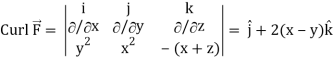

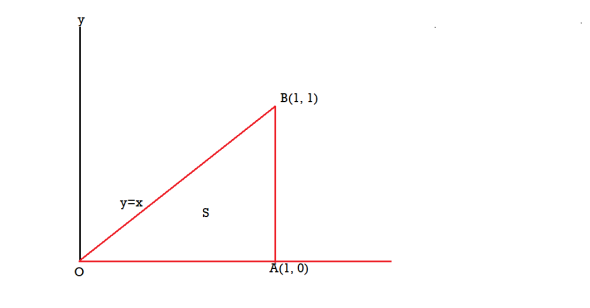
The equation of the line OB is y = x
Now by stokes theorem,
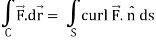
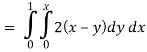
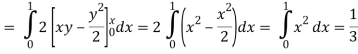
Q27) Verify Stoke’s theorem for the given function-
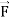 = (x+2y) dx + (y + 3x) dy
= (x+2y) dx + (y + 3x) dy
Where C is the unit circle in the xy-plane.
A27)
Suppose-
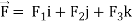

= F1dx + F2 dy + F3 dz
Here F1 = x+2y, F2 = y+ 3x, F3 = 0
We know that unit circle in xy-plane-
Or
x = cos ∅, dx = - sin ∅ d∅
y = sin ∅, dy = cos ∅ d∅
So that,
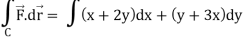
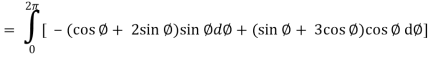

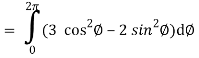

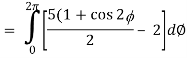
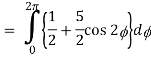
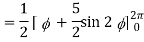
= ½ [ 2π + 0] = π
Now
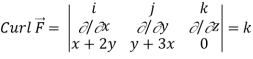
Now,
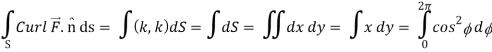
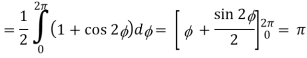
Hence the Stokes theorem is verified.