Unit - 4
Electrostatics
Q1) Explain LAPLACE’S AND POISSON’S equations for electrostatic potential.
A1) A useful approach to the calculation of electric potentials is to relate that potential to the charge density which gives rise to it. The electric field is related to the charge density by the divergence relationship
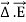 =
= 
E = Electric field
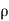 = Charge density
= Charge density
 = Permittivity
= Permittivity
And the electric field is related to the electric potential by a gradient relationship
E = 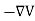
Therefore the potential is related to the charge density by Poisson's equation
 =
=  2V =
2V = 
In a charge-free region of space, this becomes Laplace's equation
 2V = 0
2V = 0
This mathematical operation, the divergence of the gradient of a function, is called the Laplacian. Expressing the Laplacian in different coordinate systems to take advantage of the symmetry of a charge distribution helps in the solution for the electric potential V.
For example, if the charge distribution has spherical symmetry, you use the Laplacian in spherical polar coordinates.
Since the potential is a scalar function, this approach has advantages over trying to calculate the electric field directly. Once the potential has been calculated, the electric field can be computed by taking the gradient of the potential.
Q2) Explain Laplace’s equations in one dimension.
A2) In one dimension the electrostatic potential V depends on only one variable x. The electrostatic potential V(x) is a solution of the one-dimensional Laplace equation
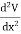 =0
=0
The general solution of this equation is
V(x) = sx + b
Where s and b are arbitrary constants. These constants are fixed when the value of the potential is specified at two different positions.
Q3) Consider a one-dimensional world with two point conductors located at x = 0 m and at x = 10 m. The conductor at x = 0 m is grounded (V = 0 V) and the conductor at x = 10 m is kept at a constant potential of 200 V. Determine V.
A3) The boundary conditions for V are
V(0) = b = 0V
And
V(10) = 10s +b =200V
The first boundary condition shows that b = 0 V. The second boundary condition shows that s = 20 V/m. The electrostatic potential for this system of conductors is thus
V(x) = 20x
The corresponding electric field can be obtained from the gradient of V
E(x) = 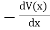 = -20 V/m
= -20 V/m
The boundary conditions used here, can be used to specify the electrostatic potential between x = 0 m and x = 10 m but not in the region x < 0 m and x > 10 m.
If the solution obtained here was the general solution for all x, then V would approach infinity when x approaches infinity and V would approach minus infinity when x approaches minus infinity. The boundary conditions therefore provide the information necessary to uniquely define a solution to Laplace's equation, but they also define the boundary of the region where this solution is valid (in this example 0 m < x < 10 m).
Q4) Explain property 1 of the one-dimensional Laplace equation.
A4) V(x) is the average of V(x + R) and V(x - R) for any R as long as x + R and x - R are located in the region between the boundary points. This property is easy to proof:
This property immediately suggests a powerful analytical method to determine the solution of Laplace's equation. If the boundary values of V are
V(x=a) =Va
And
V(x=b) =Vb
Then property 1 can be used to determine the value of the potential at (a + b)/2:
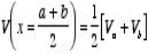
Next we can determine the value of the potential at x = (3 a + b)/4 and at
x = (a + 3 b)/4:
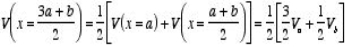
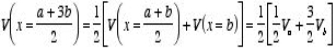
This process can be repeated and V can be calculated in this manner at any point between x = a and x = b (but not in the region x > b and x < a).
Q5) Explain Property 2 in one-dimensional Laplace’s equation.
A5) The solution of Laplace's equation cannot have local maxima or minima. Extreme values must occur at the end points (the boundaries). This is a direct consequence of property 1.
Property 2 has an important consequence: a charged particle cannot be held in stable equilibrium by electrostatic forces alone (Earnshaw's Theorem). A particle is in a stable equilibrium if it is located at a position where the potential has a minimum value.
A small displacement away from the equilibrium position will increase the electrostatic potential of the particle, and a restoring force will try to move the particle back to its equilibrium position.
There can be no local maxima or minima in the electrostatic potential.
The particle cannot be held in stable equilibrium by just electrostatic forces.
Q6) Explain Laplace’s equation in two dimension.
A6) In two dimensions the electrostatic potential depends on two variables x and y. Laplace's equation now becomes
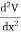 +
+  =0
=0
This equation does not have a simple analytical solution as the one-dimensional Laplace equation does. However, the properties of solutions of the one-dimensional Laplace equation are also valid for solutions of the two-dimensional Laplace equation:
Property 1:
The value of V at a point (x, y) is equal to the average value of V around this point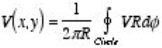
Where the path integral is along a circle of arbitrary radius, centered at (x, y) and with radius R.
Property 2:
V has no local maxima or minima; all extremes occur at the boundaries.
Q7) Explain Laplace’s equation in three dimension.
A7) In three dimensions the electrostatic potential depends on three variables x, y, and z. Laplace's equation now becomes
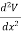 +
+  =0
=0
This equation does not have a simple analytical solution as the one-dimensional Laplace equation does. However, the properties of solutions of the one-dimensional Laplace equation are also valid for solutions of the three-dimensional Laplace equation:
Property 1:
The value of V at a point (x, y, z) is equal to the average value of V around this point

Where the surface integral is across the surface of a sphere of arbitrary radius, centered at (x,y,z) and with radius R.

Proof of property 1
To proof this property of V consider the electrostatic potential generated by a point charge q located on the z axis, a distance r away from the center of a sphere of radius R (see Figure 3.1). The potential at P, generated by charge q, is equal to
Vp= 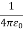

Where d is the distance between P and q. Using the cosine rule we can express d in terms of r, R and θ
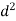 =
= +
+ -2Rrcosθ
-2Rrcosθ
The potential at P due to charge q is therefore equal to
Vp= 

The average potential on the surface of the sphere can be obtained by integrating Vp across the surface of the sphere. The average potential is equal to

Which is equal to the potential due to q at the center of the sphere. Applying the principle of superposition it is easy to show that the average potential generated by a collection of point charges is equal to the net potential they produce at the center of the sphere.
Q8) Explain property 2 in three dimensions.
A8) Property 2:
The electrostatic potential V has no local maxima or minima; all extremes occur at the boundaries.
Example:
Find the general solution to Laplace's equation in spherical coordinates, for the case where V depends only on r. Then do the same for cylindrical coordinates.
Laplace's equation in spherical coordinates is given by

If V is only a function of r then
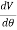 =0
=0
And
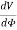 =0
=0
Therefore, Laplace's equation can be rewritten as
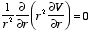
The solution V of this second-order differential equation must satisfy the following first-order differential equation:
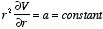
This differential equation can be rewritten as
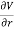 =
=
The general solution of this first-order differential equation is
V(r) =  +b
+b
Where b is a constant. If V = 0 at infinity then b must be equal to zero, and consequently
V(r)=
Laplace's equation in cylindrical coordinates is
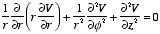
If V is only a function of r then
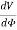 =0
=0
And
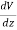 =0
=0
Therefore, Laplace's equation can be rewritten as
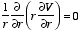
The solution V of this second-order differential equation must satisfy the following first-order differential equation:
r = a = constant
= a = constant
This differential equation can be rewritten as
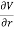 =
= 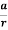
The general solution of this first-order differential equation is
V(r) = aln(r) +b
Where b is a constant. The constants a and b are determined by the boundary conditions.
Q9) Explain First Uniqueness theorem.
A9) Consider a volume within which the charge density is equal to zero. Suppose that the value of the electrostatic potential is specified at every point on the surface of this volume. The first uniqueness theorem states that in this case the solution of Laplace's equation is uniquely defined.

To proof the first uniqueness theorem we will consider what happens when there are two solutions V1 and V2 of Laplace's equation in the volume shown in Figure. Since V1 and V2 are solutions of Laplace's equation we know that
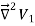 =0
=0
 =0
=0
Since both V1 and V2 are solutions, they must have the same value on the boundary. Thus V1 = V2 on the boundary of the volume. Now consider a third function V3, which is the difference between V1 and V2
 =
= -
-
The function V3 is also a solution of Laplace's equation. This can be demonstrated easily:
 =
=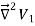 -
-  =0
=0
The value of the function V3 is equal to zero on the boundary of the volume since V1 = V2 there. However, property 2 of any solution of Laplace's equation states that it can have no local maxima or minima and that the extreme values of the solution must occur at the boundaries. Since V3 is a solution of Laplace's equation and its value is zero everywhere on the boundary of the volume, the maximum and minimum value of V3 must be equal to zero. Therefore, V3 must be equal to zero everywhere. This immediately implies that
V1 = V2
This proves that there can be no two different functions V1 and V2 that are solutions of Laplace's equation and satisfy the same boundary conditions. Therefore, the solution of Laplace's equation is uniquely determined if its value is a specified function on all boundaries of the region. This also indicates that it does not matter how you come by your solution: if (a) it is a solution of Laplace's equation, and (b) it has the correct value on the boundaries, then it is the right and only solution.

The first uniqueness theorem can only be applied in those regions that are free of charge and surrounded by a boundary with a known potential (not necessarily constant). In the laboratory the boundaries are usually conductors connected to batteries to keep them at a fixed potential.
In many other electrostatic problems we do not know the potential at the boundaries of the system. Instead we might know the total charge on the various conductors that make up the system (note: knowing the total charge on a conductor does not imply a knowledge of the charge distribution ρ since it is influenced by the presence of the other conductors).
In addition to the conductors that make up the system, there might be a charge distribution ρ filling the regions between the conductors. For this type of system the first uniqueness theorem does not apply.
Q10) Explain Second uniqueness theorem.
A10) The second uniqueness theorem states that the electric field is uniquely determined if the total charge on each conductor is given and the charge distribution in the regions between the conductors is known.
The proof of the second uniqueness theorem is similar to the proof of the first uniqueness theorem.
Suppose that there are two fields 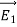 and
and 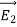 that are solutions of Poisson's equation in the region between the conductors. Thus
that are solutions of Poisson's equation in the region between the conductors. Thus
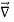 .
. =
= 
 .
. =
= 
Where ρ is the charge density at the point where the electric field is evaluated. The surface integrals of  and
and 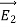 , evaluated using a surface that is just outside one of the conductors with charge Qi, are equal to
, evaluated using a surface that is just outside one of the conductors with charge Qi, are equal to  . Thus
. Thus
 =
= 
 =
= 
The difference between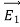 and
and 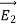 , So
, So
 =
= 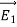 -
- 
Satisfies the following equations:
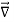 .
. =
=  .
. -
-  .
.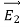
 -
-  =0
=0
 =
=  -
-  =
=  -
-  =0
=0
Consider the surface integral of  , integrated over all surfaces (the surface of all conductors and the outer surface). Since the potential on the surface of any conductor is constant, the electrostatic potential associated with
, integrated over all surfaces (the surface of all conductors and the outer surface). Since the potential on the surface of any conductor is constant, the electrostatic potential associated with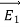 and
and 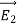 , must also be constant on the surface of each conductor.
, must also be constant on the surface of each conductor.
Therefore, 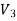 =
=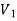 -
- will also be constant on the surface of each conductor.
will also be constant on the surface of each conductor.
The surface integral of 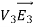 over the surface of conductor i can be written as
over the surface of conductor i can be written as
 =
= 
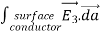 =0
=0
Since the surface integral of 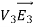 over the surface of conductor i is equal to zero,
over the surface of conductor i is equal to zero,
The surface integral of  over all conductor surfaces will also be equal to zero. The surface integral of
over all conductor surfaces will also be equal to zero. The surface integral of  over the outer surface will also be equal to zero since
over the outer surface will also be equal to zero since 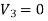 on this surface. Thus
on this surface. Thus
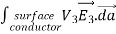 =0
=0
The surface integral 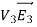 of can be rewritten using Green's identity as
of can be rewritten using Green's identity as
0 = 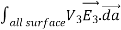 = -
= -  =
= 
= - 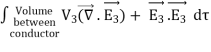 = -
= - 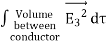 =0
=0
Where the volume integration is over all space between the conductors and the outer surface. Since is always positive, the volume integral of
is always positive, the volume integral of 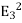 can only be equal to zero if
can only be equal to zero if 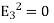 everywhere. This implies immediately that
everywhere. This implies immediately that 
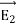 , everywhere, and proves the second uniqueness theorem.
, everywhere, and proves the second uniqueness theorem.
Q11) Explain electric polarization.
A11) Electric polarization refers to the separation of center of positive charge and the center of negative charge in a material. The separation can be caused by a sufficiently high-electric field.
It occurs when a non-polar substance is placed between two parallel plates with an applied electric field. The electric field tends to attract the negatively charged electron particles or clouds towards the positive plate and the positive charge nucleus towards the negative plate. Therefore, in the presence of an electric field or current, there will be observed an electrical distortion or polarized molecule to form an electrical dipole. In learning chemistry or physics, such type of distortion process in the molecules is called the electric polarization but the polarization disappears as soon as the polarized field is withdrawn and the polarizing molecule comes back to its original state.
Q12) Explain the relation between D, E and P.
A12) The permittivity εo of free space is 8.854×10-12 farads/meter, where
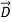 =εo
=εo 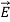 .
.
The permittivity ε of any material deviates from εo for free space if applied electric fields induce electric dipoles in the medium; such dipoles alter the applied electric field seen by neighbouring atoms.
Electric fields generally distort atoms because 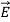 pulls on positively charged nuclei (f=q
pulls on positively charged nuclei (f=q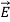 [N]) and repels the surrounding negatively charged electron clouds. The resulting small offset d of each atomic nucleus of charge +q relative to the center of its associated electron cloud produces a tiny electric dipole in each atom, as suggested in Figure a.
[N]) and repels the surrounding negatively charged electron clouds. The resulting small offset d of each atomic nucleus of charge +q relative to the center of its associated electron cloud produces a tiny electric dipole in each atom, as suggested in Figure a.
In addition, most asymmetric molecules are permanently polarized, such as H2O or NH3, and can rotate within fluids or gases to align with an applied field. Whether the dipole moments are induced, or permanent and free to rotate, the result is a complete or partial alignment of dipole moments as suggested in
These polarization charges generally cancel inside the medium, as suggested in Figure b, but the immobile atomic dipoles on the outside surfaces of the medium are not fully cancelled and therefore contribute the surface polarization charge ρsp

Above figure suggests how two charged plates might provide an electric field  that polarizes a dielectric slab having permittivity ε > εo. The electric field
that polarizes a dielectric slab having permittivity ε > εo. The electric field 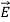 is the same in vacuum as it is inside the dielectric (assuming no air gaps) because the path integral of
is the same in vacuum as it is inside the dielectric (assuming no air gaps) because the path integral of  from plate to plate equals their voltage difference V in both cases. The electric displacement vector
from plate to plate equals their voltage difference V in both cases. The electric displacement vector  e =ε
e =ε  and therefore differs.] We associate the difference between
and therefore differs.] We associate the difference between 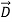 o =εo
o =εo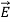 (vacuum) and
(vacuum) and 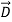 ε=ε
ε=ε (dielectric) with the electric polarization vector P, where:
(dielectric) with the electric polarization vector P, where:
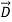 = ε
= ε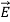 =εo
=εo  +
+ = εo
= εo  (1+
(1+ ) (8)
) (8)
The polarization vector 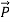 is defined by (8) and is normally parallel to
is defined by (8) and is normally parallel to 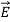 in the same direction, as shown in Figure: c ; it points from the negative surface polarization charge to the positive surface polarization charge (unlike
in the same direction, as shown in Figure: c ; it points from the negative surface polarization charge to the positive surface polarization charge (unlike 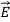 , which points from positive charges to negative ones).
, which points from positive charges to negative ones).
As suggested in (8),  = εo
= εo  ,
,
Where χ is defined as the dimensionless susceptibility of the dielectric. Because nuclei are bound rather tightly to their electron clouds, χ is generally less than 3 for most atoms, although some molecules and crystals, particularly in fluid form, can exhibit much higher values.
Electric displacement, also known as dielectric displacement and usually denoted by D, is a vector field in a non-conducting medium, a dielectric.
In a dielectric material, the presence of an electric field E causes the bound positive and negative charges in the material to slightly separate, inducing a local electric dipole moment. The electric displacement field "D" is defined as
D= 𝜺0E+P
E = External electric field in which the dielectric is placed
𝜺0 = the permittivity of the free space
P = Polarization Density
In S.I. System, Unit of Electric displacement is C/m2.
D = 𝜺0E+P
D= 𝜺E and P = XeE