UNIT 1
INTRODUCTION TO MECHANICS
1Question: Discuss the fundamental forces in nature?
Solution:
A fundamental force of nature is an attraction or repulsion between objects as described through interactions between fields and particles.
Physics has identified four basic types of these interactions, which together describe every action we see in the Universe, from the decay of atomic particles to the drift of entire galaxies.
From walking on the street, to launching a rocket into space, to sticking a magnet on your refrigerator, physical forces are acting all around us. But all the forces that we experience every day (and many that we don't realize we experience every day) can be whittled down to just four fundamental forces:
- Electromagnetic Force
- Gravitational Force
- Strong Nuclear Force
- Weak Nuclear Force
These are called the four fundamental forces of nature, and they govern everything that happens in the universe.
- Electromagnetic Force
This is the second strongest force after the strong force and it acts on electrically charged particles. It has strength of 1/137 relative to the strong force but has an infinite range. However, this force has both attractive and repulsive properties due to the two charges it possesses; negative and positive. Objects of like charge will have a repulsive effect on each other, while objects of unlike charges will have an attractive effect and this can be demonstrated with a simple magnet or electric charges.
This is the force that's most obvious in our day-to-day lives. Thanks to the interactions of negatively-charged electrons and positively-charged protons, it allows single atoms to combine into different materials. The force is also carried through the electromagnetic field by a particle called a photon, which thanks to chemical changes in our eyes our bodies sense as light.
For the sake of convenience, we distinguish the two different kinds of charges by associating an algebraic sign with q, and for this reason we talk about negative and positive charges. The electrostatic force Fb on charge qb due to charge qa is given by Coulomb's law: k is a constant of proportionality and rab is a unit vector which points from a to b. If qa and qb are both negative or both positive, the force is repulsive, but if the charges are of different sign, Fb is attractive.
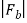 = -
= - 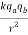
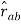
In the SI system, the unit of charge is the coulomb, abbreviated C. (The coulomb is defined in terms of electric currents and magnetic forces.) In this system, k is found by experiment to be
k = 8.99 x 109 N·m2/C2
2. Gravitational Force
This force is the weakest but has an infinite range. It has strength of 6 × 10-39 in comparison to the strength of the strong force. This force is always attractive acts between any two pieces of matter in nature. The effect of this gravitational force is dependent upon the mass of the two bodies and the distance between them.
Gravity is an attractive force between masses, which according to general relativity occurs as a result of the effect of energy acting on a space-time field. While theory suggests it could have a mediating particle - called a graviton - experiments are yet to support its existence.
While gravity might appear to be a strong force, responsible for holding entire galaxies together and squeezing the literal daylight out of stars, it's approximately 1029 times weaker than the weak nuclear force. That means it has virtually no observable effect on the scale of tiny particles, becoming relevant only on a more cosmic level.
Consider two particles, a and b, with masses Ma and Mb, respectively, separated by distance r. Let Fb be the force exerted on particle b by particle a.
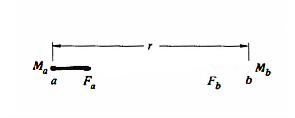
Figure 1
Our verbal description of the magnitude of the force is summarized by
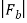 =
= 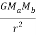
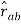
G is a constant of proportionality called the gravitational constant. Its value is found by measuring the force between masses in a known geometry. The first measurements were performed by Henry Cavendish in 1771 using a torsion balance.
The modern value of G is 6.67 X 10-11 N·m2/kg2. (G is the least accurately known of the fundamental constants. Perhaps you can devise a new way to measure it more precisely.) Experimentally, G is the same for all materials-aluminum, lead, neutrons, or what have you. For this reason, the law is called the universal law of gravitation.
3. Strong Nuclear Force
The strong nuclear force is what holds together the nuclei of atoms. This force holds the nucleus of an atom together. It is the strongest of the forces, but it is very short ranged. It acts over a range of about 10-15m, which is the average diameter of a medium sized nucleus. This force is attractive.
The protons and neutrons making up an atom's nucleus are themselves made up of a trio of simpler particles called quarks. A particle called a gluon acts on a property of quarks called colour, creating the force's pull.
Unlike the other three fundamental forces, the further the gluon needs to travel, the stronger the nuclear force gets. On the scale of protons and neutrons, this spring-like effect makes it incredibly hard to pull quarks apart. This helps explain why the strong force is so, well, strong.
On a scale of an atom's entire nucleus, the force also binds whole protons and neutrons to each other. Protons also push each other away thanks to the electromagnetic force, putting atomic nuclei into a delicate balance.
4. Weak Nuclear Force
This force is weak compared to the strong force as the name implies and has the shortest range of 10-18m, which is 0.1% of the diameter of a proton. It is responsible for radioactive decay especially nuclear beta decay. All particles experience this force.
Of all the fundamental forces, the weak nuclear force is the trickiest to grasp. It describes how the quarks that make up nuclear particles can change from one form into another. The force is carried by particles called W and Z bosons.
The weak force acts over an incredibly short distance, equal to about 0.1 percent of the diameter of a proton. When a particle such as a neutrino comes right up close to a quark, the weak force causes the quark to change by sending out a W boson. This can turn a neutron into a proton (creating a whole new element in the process), and the neutrino into an electron.
So We have studied that every pair of particles in the universe had its own special interaction, the task would be impossible. Fortunately, nature is kinder than this. As far as we know, there are only four fundamentally different types of interactions in the universe: gravity, electromagnetic interactions, the so-called weak interaction, and the strong interaction. Gravity and the electromagnetic interactions can act over a long range because they decrease only as the inverse square of the distance. However, the gravitational force always attracts, whereas electrical forces can either attract or repel. In large systems, electrical attraction and repulsion cancel to a high degree, and gravity alone is left. For this reason, gravitational forces dominate the cosmic scale of our universe. In contrast, the world immediately around us is dominated by the electrical forces, since they are far stronger than gravity on the atomic scale. Electrical forces are responsible for the structure of atoms, molecules, and more complex forms of matter, as well as the existence of light. The weak and strong interactions have such short ranges that they are important only at nuclear distances, typically 10-16 m.
They are negligible even at atomic distances, 10-10 m. As its name implies, the strong interaction is very strong, much stronger than the electromagnetic force at nuclear distances. It is the "glue" that binds the atomic nucleus, but aside from this it has little effect in the everyday world. The weak interaction plays a less dramatic role; it mediates in the creation and destruction of neutrinos-particles of no mass and no charge which are essential to our understanding of matter but which can be detected only by the most arduous experiments. Our object in the remainder of the chapter is to become familiar with the forces which are important in everyday mechanics. Two of these, the forces of gravity and electricity, are fundamental and cannot be explained in simpler terms. The other forces we shall discuss, friction, the contact force, and the viscous force, can be understood as the macroscopic manifestation of interatomic forces.
2 Question: Discuss the transformation of scalars and vectors under rotation transformation?
Solution:
Certain physical quantities such as mass or the absolute temperature at some point in space only have magnitude. A single number can represent each of these quantities, with appropriate units, which are called scalar quantities. There are, however, other physical quantities that have both magnitude and direction. Force is an example of a quantity that has both direction and magnitude (strength). Three numbers are needed to represent the magnitude and direction of a vector quantity in a three dimensional space. These quantities are called vector quantities.
Vector quantities also satisfy two distinct operations, vector addition and multiplication of a vector by a scalar. We can add two forces together and the sum of the forces must satisfy the rule for vector addition. We can multiply a force by a scalar thus increasing or decreasing its strength. Position, displacement, velocity, acceleration, force, and momentum are all physical quantities that can be represented mathematically by vectors. The set of vectors and the two operations form what is called a vector space. There are many types of vector spaces but we shall restrict our attention to the very familiar type of vector space in three dimensions that most students have encountered in their mathematical courses.
Vectors are sets of three quantities that transform in the same manner as the coordinates of a point P.
- Having a magnitude and direction is not sufficient to define a vector.
- Some transformations cannot be written in terms of a series of rotations. An example is an inversion. These are called improper rotations.
- Transformations that can be written in terms of a series of rotations are called proper rotations.
The laws of Physics are invariant'' under rotations of the coordinate system.
Rotational symmetry of laws of Physics implies conservation of Angular Momentum.
We will work with Passive Rotations'' where we rotate the coordinate axes rather than active rotations'' where we rotate the physical system and keep the axes fixed. These are essentially the same thing except the rotation angle changes sign.
A vector is a mathematical object that transforms in a particular way under rotations.
We know there are also physical quantities called scalars that are invariant under rotations.
Very often in practical problems, the components of a vector are known in one coordinate system but it is necessary to find them in some other coordinate system.
The relationship between the components in one coordinate system and the components in a second coordinate system are called the transformation equations. Any change of Cartesian coordinate system will be due to a translation of the base vectors and a rotation of the base vectors. A translation of the base vectors does not change the components of a vector.
Rotation of object relative to FIXED axis:
Basic equations you can get by looking at the diagram above:
x1= rcosα…………(1)
x2=rcos(θ+α)…………(2)
y1=rsinα…………(3)
y2=rsin(θ+α)…………(4)
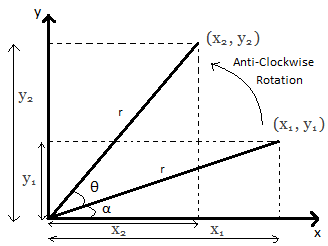
Figure: 1
Using trigonometric results the equations (2) and (4) become
x2=rcos(θ+α)
=rcosθcosα–rsinθsinα
=(rcosα)cosθ–(rsinα)sinθ
=x1cosθ–y1sinθ…………(5)
y2=rsin(θ+α)
=rsinθcosα+rcosθsinα
=(rcosα)cosθ+(rsinα)cosθ
=x1sinθ+y1cosθ…………(6)
Hence, For an anti-clockwise rotation,
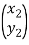 =
= 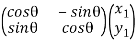 …………(7)
…………(7)
Is called the rotation matrix. Its determinant is 1.
To find the clockwise rotation matrix, you can do the calculations again. OR you can just transpose the above matrix OR you can substitute −θ into the matrix.
Hence, the clockwise rotation matrix is: 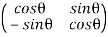
Note: Since clockwise rotation means rotating in the anti-clockwise direction by −θ, you can just substitute −θ into the anti-clockwise matrix to get the clockwise matrix. Since cos is an even function, it will not be affected by the −θ. (- cos x = cos x)
Rotation of coordinate axes:
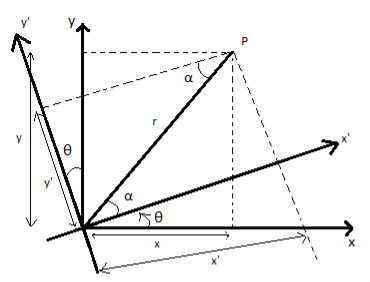
Figure: 2
Basic equations:
x′=rcosα…………(8)
x=rcos(θ+α) …………(9)
y′=rsin…………(10)
y=rsin(θ+α) …………(11)
Using trigonometric results the equations (9) and (11) become
x=rcos(θ+α)
=rcosθcosα–rsinθsinα
=x′cosθ–y′sinθ…………(12)
y=rsin(θ+α)
=rsinθcosα+rcosθsinα
=x′sinθ+y′cosθ…………(13)
From equation (13) So we have
x′=  …………(14)
…………(14)
y′= 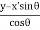 …………(15)
…………(15)
Substitute the above (14) and (15) equations into equation (12) and you will get:
y′=−xsinθ+ycosθ
x′=xcosθ+ysinθ
Hence,
 =
= 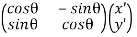 …………(16)
…………(16)
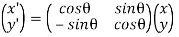 …………(17)
…………(17)
3 Question: State Newton’s first law of motion? Discuss it by giving some example?
Solution:
How do the forces that act on a body affect its motion? To begin to answer this question, let’s first consider what happens when the net force on a body is zero. You would almost certainly agree that if a body is at rest, and if no net force acts on it (that is, no net push or pull), that body will remain at rest. But what if there is zero net force acting on a body in motion? To see what happens in this case, suppose you slide a hockey puck along a horizontal table top, applying a horizontal force to it with your hand (Figure 2).
Figure 2: Table: puck stops short
After you stop pushing, the puck does not continue to move indefinitely; it slows down and stops. To keep it moving, you have to keep pushing (that is, applying a force). You might come to the “common sense” conclusion that bodies in motion naturally come to rest and that a force is required to sustain motion.
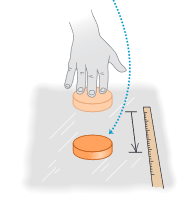
Figure 3: Table: Ice: puck slides farther
But now imagine pushing the puck across a smooth surface of ice (Figure 3). After you quit pushing, the puck will slide a lot farther before it stops. Put it on an air-hockey table, where it floats on a thin cushion of air, and it moves still farther (Figure 4).
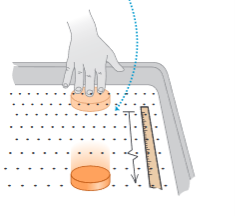
Figure 4: Air-hockey table: puck slides even farther
In each case, what slows the puck down is friction, an inter-action between the lower surface of the puck and the surface on which it slides. Each surface exerts a friction force on the puck that resists the puck’s motion; the difference in the three cases is the magnitude of the friction force. The ice exerts less friction than the table top, so the puck travels farther. The gas molecules of the air-hockey table exert the least friction of all.
If we could eliminate friction completely, the puck would never slow down, and we would need no force at all to keep the puck moving once it had been started. Thus the “common sense” idea that a force is required to sustain motion is incorrect. Experiments like the ones we’ve just described show that when no net force acts on a body, the body either remains at rest or moves with constant velocity in a straight line. Once a body has been set in motion, no net force is needed to keep it moving. We call this observation Newton’s first law of motion.
Newton’s First law can also be written as
A body acted on by no net force has a constant velocity (which may be zero) and zero acceleration
The tendency of a body to keep moving once it is set in motion is called inertia.
It’s important to note that the net force is what matters in Newton’s first law
Example
Suppose a hockey puck rests on a horizontal surface with negligible friction, such as an air-hockey table or a slab of wet ice.

Figure 5: (a) A hockey puck accelerates in the direction of a net applied force 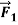 . (b) When the net force is zero, the acceleration is zero, and the puck is in equilibrium.
. (b) When the net force is zero, the acceleration is zero, and the puck is in equilibrium.
If the puck is initially at rest and a single horizontal force 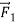 acts on it (Figure 5a), the puck starts to move. If the puck is in motion to begin with, the force changes its speed, its direction, or both, depending on the direction of the force. In this case the net force is equal to
acts on it (Figure 5a), the puck starts to move. If the puck is in motion to begin with, the force changes its speed, its direction, or both, depending on the direction of the force. In this case the net force is equal to 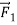 which is not zero. (There are also two vertical forces: the earth’s gravitational attraction and the upward normal force exerted by the surface. But as we mentioned earlier, these two forces cancel.)
which is not zero. (There are also two vertical forces: the earth’s gravitational attraction and the upward normal force exerted by the surface. But as we mentioned earlier, these two forces cancel.)
Now suppose we apply a second force, 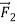 (Figure 5b), equal in magnitude to
(Figure 5b), equal in magnitude to 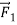 but opposite in direction. The two forces are negatives of each other,
but opposite in direction. The two forces are negatives of each other,
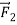
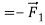 ,and their vector sum is zero
,and their vector sum is zero

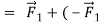
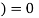
Again, we find that if the body is at rest at the start, it remains at rest; if it is initially moving, it continues to move in the same direction with constant speed. These results show that in Newton’s first law, zero net force is equivalent to no force at all. This is just the principle of superposition of forces.
When a body is either at rest or moving with constant velocity (in a straight line with constant speed), we say that the body is in equilibrium. For a body to be in equilibrium, it must be acted on by no forces, or by several forces such that their vector sum that is, the net force is zero.
4 Question: Derive Newton’s equations of motion in polar coordinates?
Solution:
Although Newton’s 2nd law takes a simple form in Cartesian coordinates, there are many circumstances where the symmetry of the problem lends itself to other coordinates.
To illustrate this, let’s take a look at 2-d polar coordinates. You should already have some familiarity with these, but we will see that certain complexities arise that require a bit of care.
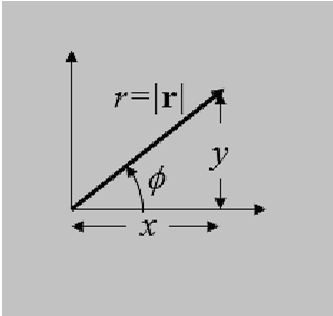
Figure 9
First of all you can go back and forth between Cartesian and polar coordinates by the familiar
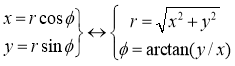
We now wish to introduce unit vectors for these new polar coordinates, (r, ϕ), which we will write 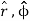 . Remember, these have to be 1 unit long, and point in the direction of r and ϕ.
. Remember, these have to be 1 unit long, and point in the direction of r and ϕ.
One way to construct a unit vector is to take any vector r and divide by its length |r|. Clearly, such a unit vector is in the direction of r but has unit length.
There is a major difference between the behavior of the cartesian unit vectors and the corresponding ones for polar coordinates.

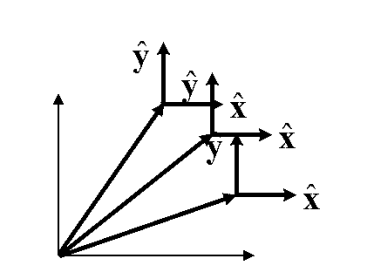
Figure 10: Cartesian unit vectors are constant
Figure 11: Polar coordinate unit vectors change (direction) with time
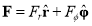 Since
Since 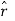 and
and  are perpendicular vectors in our two-dimensional space, any vector can be split into components in terms of them. For instance, the force F can be written:
are perpendicular vectors in our two-dimensional space, any vector can be split into components in terms of them. For instance, the force F can be written:
Imagine twirling a stone at the end of a string. Then the force Fr on the stone is just the tension in the string, and Fϕ might be the force of air resistance as the stone flies through the air.
The position vector is then particularly simple: r =r
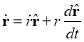 But to solve Newton’s 2nd law, F =m
But to solve Newton’s 2nd law, F =m , we need the second derivative of r. Let’s just take the derivative using the product rule:
, we need the second derivative of r. Let’s just take the derivative using the product rule:
Where we keep the second term because now the unit vector 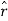 is not constant.
is not constant.
To see what the derivative of the unit vector is, let’s look at how 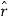 changes.
changes.
As the coordinate r changes from time t1 to time t2= t1 + Dt, the unit vector changes by:
We know that arc length = rθ
In this case, θ = 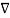 ϕ and r =
ϕ and r = 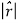 =1
=1
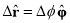

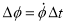 We can rewrite
We can rewrite
Hence
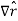 =
= 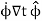
Or, after taking the limit as  t approaches zero, we have
t approaches zero, we have
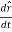 =
=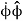
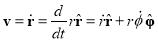 Thus, our first derivative is
Thus, our first derivative is
So the components of v are
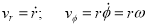
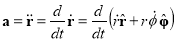 Now we need to take another derivative to get
Now we need to take another derivative to get
This is going to involve a time derivative of the  unit vector, for which we use much the same procedure as before.
unit vector, for which we use much the same procedure as before.
Since the 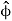 unit vector is perpendicular to the
unit vector is perpendicular to the  unit vector, we have the same geometry as before, except rotated 90 degrees.
unit vector, we have the same geometry as before, except rotated 90 degrees.
The change  is now in the
is now in the 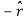 direction, and its length is again
direction, and its length is again

 ,
,
So finally we have:
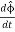 =
=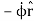
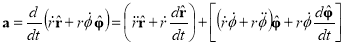 All that remains is to do a careful, term-by-term derivative to get
All that remains is to do a careful, term-by-term derivative to get
And then plug in our new-found expressions for the derivatives of the unit vectors.
And our expressions for the unit vector derivatives:
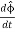 =
=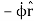
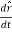 =
=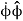
We have finally:
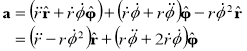
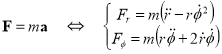 Now that we have the acceleration, we are ready to write down Newton’s 2nd law in polar coordinates.
Now that we have the acceleration, we are ready to write down Newton’s 2nd law in polar coordinates.
This is the required result.
5 Question: State Newton’s second law of motion? Discuss it by giving some example?
Solution:
Newton’s first law tells us that when a body is acted on by zero net force, the body moves with constant velocity and zero acceleration. In Figure 6(a), a hockey puck is sliding to the right on wet ice. There is negligible friction, so there are no horizontal forces acting on the puck; the downward force of gravity and the upward normal force exerted by the ice surface sum to zero. So the net force  acting on the puck is zero, the puck has zero acceleration, and its velocity is constant.
acting on the puck is zero, the puck has zero acceleration, and its velocity is constant.
But what happens when the net force is not zero?
In Figure 6 (b) we apply a constant horizontal force to a sliding puck in the same direction that the puck is moving. Then 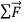 is constant and in the same horizontal direction as
is constant and in the same horizontal direction as 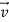 . We find that during the time the force is acting, the velocity of the puck changes at a constant rate; that is, the puck moves with constant acceleration. The speed of the puck increases, so the acceleration
. We find that during the time the force is acting, the velocity of the puck changes at a constant rate; that is, the puck moves with constant acceleration. The speed of the puck increases, so the acceleration 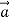 is in the same direction as
is in the same direction as 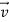 and
and 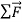 .
.
In Figure 6(c) we reverse the direction of the force on the puck so that 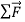 acts opposite to
acts opposite to 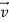 . In this case as well, the puck has acceleration; the puck moves more and more slowly to the right. The acceleration
. In this case as well, the puck has acceleration; the puck moves more and more slowly to the right. The acceleration 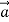 in this case is to the left, in the same direction as
in this case is to the left, in the same direction as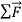 . As in the previous case, experiment shows that the acceleration is constant if
. As in the previous case, experiment shows that the acceleration is constant if 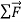 is constant. We conclude that net force acting on a body causes the body to accelerate in the same direction as the net force. If the magnitude of the net force is constant, as in Figures 6(b) and 6(c), then so is the magnitude of the acceleration.
is constant. We conclude that net force acting on a body causes the body to accelerate in the same direction as the net force. If the magnitude of the net force is constant, as in Figures 6(b) and 6(c), then so is the magnitude of the acceleration.
Figure 6: Using a hockey puck on a friction-less surface to explore the relationship between the net force  on a body and the resulting acceleration
on a body and the resulting acceleration  of the body.
of the body.
Our results mean that for a given body, the ratio of the magnitude  of the net force to the magnitude a=
of the net force to the magnitude a=  of the acceleration is constant, regardless of the magnitude of the net force. We call this ratio the inertial mass, or simply the mass, of the body and denote it by m. That is,
of the acceleration is constant, regardless of the magnitude of the net force. We call this ratio the inertial mass, or simply the mass, of the body and denote it by m. That is,
m= 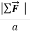 or
or 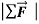 =ma or a=
=ma or a= 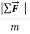
Mass is a quantitative measure of inertia. The above equations says that the greater a body’s mass, the more the body “resists” being accelerated. When you hold a piece of fruit in your hand at the supermarket and move it slightly up and down to estimate its heft, you’re applying a force and seeing how much the fruit accelerates up and down in response. If a force causes a large acceleration, the fruit has a small mass; if the same force causes only a small acceleration, the fruit has a large mass.
One newton is the amount of net force that gives an acceleration of 1 meter per second squared to a body with a mass of 1 kilogram.
For the same net force, the ratio of the masses of two bodies is the inverse of the ratio of their accelerations.
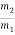 =
= 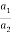 So Newton’s second law States that
So Newton’s second law States that
If a net external force acts on a body, the body accelerates. The direction of acceleration is the same as the direction of the net force. The mass of the body times the acceleration vector of the body equals the net force vector
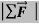 =ma
=ma
Newton’s second law is a fundamental law of nature, the basic relationship be-tween force and motion.
The statement of Newton’s second law refers to external forces. It’s impossible for a body to affect its own motion by exerting a force on itself; if it were possible, you could lift yourself to the ceiling by pulling up on your belt. That’s why only external forces are included in the sum  .
.
The design of high-performance motorcycles depends fundamentally on Newton’s second law. To maximize the forward acceleration, the designer makes the motorcycle as light as possible (that is, minimizes the mass) and uses the most powerful engine possible (thus maximizing the forward force).Light weight body (small m)Powerful engine (large F)application Blame Newton’s Second Law.
The above equations are valid only when the mass m is constant. It ’s easy to think of systems whose masses change, such as a leaking tank truck, a rocket ship, or a moving railroad car being loaded with coal. Such systems are better handled by using the concept of momentum.
Finally, Newton’s second law is valid in inertial frames of reference only, just like the first law. Thus it is not valid in the reference frame of any of the accelerating vehicles relative to any of these frames; the passenger accelerates even though the net force on the passenger is zero. We will usually assume that the earth is an adequate approximation to an inertial frame, although because of its rotation and orbital motion it is not precisely inertial.
Here is something important to discuss that m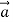 is not a force even though the vector m
is not a force even though the vector m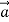 is equal to the vector sum
is equal to the vector sum  of all the forces acting on the body, the vector m
of all the forces acting on the body, the vector m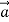 is not a force. Acceleration is a result of a nonzero net force; it is not a force itself. It’s “common sense” to think that there is a “force of acceleration” that pushes you back into your seat when your car accelerates forward from rest. But there is no such force; instead, your inertia causes you to tend to stay at rest relative to the earth, and the car accelerates around you, The “common sense” confusion arises from trying to apply Newton’s second law where it isn’t valid—in the non-inertial reference frame of an accelerating car. We will always examine motion relative to inertial frames of reference only.
is not a force. Acceleration is a result of a nonzero net force; it is not a force itself. It’s “common sense” to think that there is a “force of acceleration” that pushes you back into your seat when your car accelerates forward from rest. But there is no such force; instead, your inertia causes you to tend to stay at rest relative to the earth, and the car accelerates around you, The “common sense” confusion arises from trying to apply Newton’s second law where it isn’t valid—in the non-inertial reference frame of an accelerating car. We will always examine motion relative to inertial frames of reference only.
6 Question: State Newton’s third law of motion? Discuss it by giving some example?
Solution:
Force acting on a body is always the result of its interaction with another body, so forces always come in pairs. You can’t pull on a doorknob without the door-knob pulling back on you. When you kick a football, the forward force that your foot exerts on the ball launches it into its trajectory, but you also feel the force the ball exerts back on your foot. In each of these cases, the force that you exert on the other body is in the opposite direction to the force that body exerts on you. Experiments show that whenever two bodies interact, the two forces that they exert on each other are always equal in magnitude and opposite in direction. This fact is called Newton’s third law of motion:
If body A exerts a force on body B (an “action”), then body B exerts a force on body A (a “reaction”). These two forces have the same magnitude but are opposite in direction. These two forces act on different bodies.
Or
To every action there is equal and opposite reaction.
For example, in Figure (7)  A on B is the force applied by body A (first sub-script) on body B (second subscript), and
A on B is the force applied by body A (first sub-script) on body B (second subscript), and  B on A is the force applied by body B(first subscript) on body A (second subscript).
B on A is the force applied by body B(first subscript) on body A (second subscript).
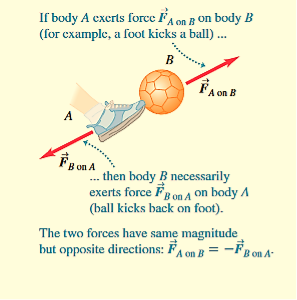
Figure 7: Newton’s third law of motion
In equation form,
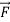 A on B =
A on B =  B on A
B on A
In the statement of Newton’s third law, “action” and “reaction” are the two opposite forces; we sometimes refer to them as an action–reaction pair. This is not meant to imply any cause-and-effect relation-ship; we can consider either force as the “action” and the other as the “reaction.” We often say simply that the forces are “equal and opposite,” meaning that they have equal magnitudes and opposite directions. The two forces in an action–reaction pair act on different bodies We stress that the two forces described in Newton’s third law act on different bodies.
The action and reaction forces are contact forces that are present only when the two bodies are touching. But Newton’s third law also applies to long-range forces that do not require physical contact, such as the force of gravitational attraction. A table-tennis ball exerts an upward gravitational force on the earth that’s equal in magnitude to the downward gravitational force the earth exerts on the ball. When you drop the ball, both the ball and the earth accelerate toward each other. The net force on each body has the same magnitude, but the earth’s acceleration is microscopically small because its mass is so great. Nevertheless, it does move.
7 Question: Prove that Newton’s second law of motion is invariant under transformation?
Solution:
Suppose there are two reference frames (systems) designated by S and S' such that the coordinate axes are parallel. In S, we have the co-ordinates {x,y,z,t} and in S' we have the co-ordinates {x’,y’,z’,t’}. S' is moving with respect to S with velocity v (as measured in S) in the x direction. The clocks in both systems were synchronised at time t=0 and they run at the same rate.
![\includegraphics[width=0.7\textwidth]{ref_frames.eps}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1650844961_9178767.png)
Figure 8 : Reference frame S' moves with velocity v (in the x direction) relative to reference frame S.
We have the intuitive relationships
x’ = x-vt
y’=y
z’=z
t’=t
This set of equations is known as the Galilean Transformation. They enable us to relate a measurement in one inertial reference frame to another. For example, suppose we measure the velocity of a vehicle moving in the in x-direction in system S, and we want to know what would be the velocity of the vehicle in S'.
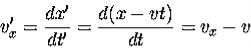 ………..(1)
………..(1)
This is the result our intuition is familiar with.
We have stated the we would like the laws of physics to be the same in all inertial reference frames, as this is indeed our experience of nature. Physically, we should be able to perform the same experiments in different reference frames, and find always the same physical laws. Mathematically, these laws are expressed by equations. So, we should be able to transform'' our equations from one inertial reference frame to the other inertial reference frame, and always find the same answer.
We will check that Newton's Second Law is the same in two different reference frames. We put one observer in the un-primed frame and the other in the primed frame, moving with velocity 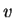 relative to the un-primed frame. Consider the vehicle of the previous case undergoing a constant acceleration in the x-direction,
relative to the un-primed frame. Consider the vehicle of the previous case undergoing a constant acceleration in the x-direction,
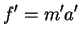

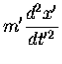

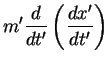

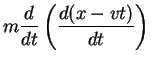

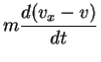
v is constant so we have

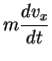

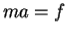
Indeed, it does not matter which inertial frame we observe from, we recover the same Second Law of Motion each time. We say the Second Law of Motion is invariant under the Galilean Transformation.
8 Question: Transform rectangular coordinates in spherical coordinates?
Solution:
Spherical coordinates are similar to the way we describe a point on the surface of the earth using latitude and longitude. By specifying the radius of a sphere and the latitude and longitude of a point on the surface of that sphere, we can describe any point in R3. To describe the latitude and longitude, we use two angles: θ (the angle from the positive x axis) and ϕ (the angle from the positive z axis). We therefore have three coordinates (ρ,θ,ϕ), where ρ is the radius of the sphere.
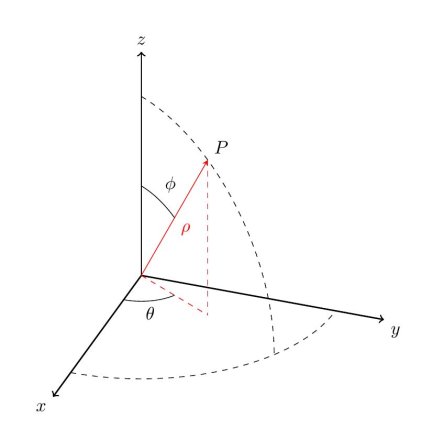
Figure 15
Where the first component is the distance from the origin to the point, the second component is the polar angle and the third component is the altitude angle measured from the positive z-axis to the line connecting the origin and the point.
Note that
0≤θ<2π
0≤ϕ≤π
ρ≥0
The formulas that we need in order to convert between rectangular and spherical coordinates are given below, without derivation
ρ=x2+y2+z2
x=ρcosθsinϕ
y=ρsinθsinϕ
z=ρcosϕ
9 Question: Convert (3, π/4, 4) in cylindrical coordinates to rectangular coordinates.
Solution:
Use the formulas, noting that r=3, θ=π/4, and z=4.
x=rcosθ=3cosπ/4= 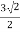
y=rsinθ=3sinπ/4= 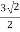
z=4
Therefore point is (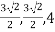 ) in rectangular coordinates.
) in rectangular coordinates.
To go in the other direction (from rectangular coordinates to cylindrical), use the following set of formulas (again, the first two are exactly what we use to convert from rectangular to polar in R2:
r=x2+y2
θ=tan−1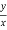
z=z
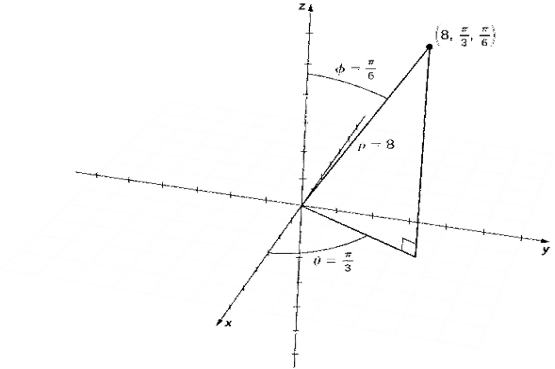
10 Question: Plot the point with spherical coordinates (8, π/3, π/6) and express its location in both rectangular and cylindrical coordinates.
Solution:
Use the equations in Note to translate between spherical and cylindrical coordinates
ρ=x2+y2+z2
x=ρcosθsinϕ = 8sin(π/6)cos(π/3) = 8(1/2)1/2=2
y=ρsinθsinϕ =8sin(π/6)sin(π/3)=8(1/2)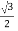 =2
=2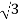
z=ρcosϕ =ρcosφ =8cos(π/6)= 8(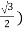 =4
=4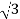
The point with spherical coordinates (8,π/3,π/6) has rectangular coordinates (2, 2 4
4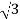 )
)
Finding the values in cylindrical coordinates is equally straightforward:
r=ρsinφ=8sinπ/6= 4
θ= θ
z=ρcosφ=8cosπ/6= 4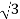
Thus, cylindrical coordinates for the point are (4,π/3, 4 )
)
.

11 Question: Define Friction
Solution:
Friction cannot be described by a simple formula, but macroscopic mechanics is hard to understand without some idea of the properties of friction. Friction arises when the surface of one body moves, or tries to move, along the surface of a second body. The magnitude of the force of friction varies in a complicated way with the nature of the surfaces and their relative velocity. In fact, the only thing we can always say about friction is that it opposes the motion which would occur in its absence.
For instance, suppose that we try to push a book across a table. If we push gently, the book remains at rest; the force of friction assumes a value equal and opposite to the tangential force we apply. In this case, the force of friction assumes whatever value is needed to keep the book at rest. However, the friction force cannot increase indefinitely. If we push hard enough, the book starts to slide. For many surfaces the maximum value of the friction is found to be equal to μN, where N is the normal force and μ is the coefficient of friction. When a body slides across a surface, the friction force is directed opposite to the instantaneous velocity and has magnitude μN.
For two given surfaces the force of sliding friction is essentially independent of the area of contact.
12 Question: A block of mass m rests on a fixed wedge of angle θ. The coefficient of friction is μ. (For wooden blocks, μ is of the order of 0.2 to 0.5.) Find the value of θ at which the block starts to slide?
Solution:

Figure 12
In the absence of friction, the block would slide down the plane; hence the friction force f Points up the plane. With the coordinates shown, we have
m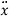 = Wsinθ – f
= Wsinθ – f
And
m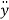 = N -Wcos
= N -Wcos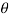 = 0.
= 0.
When sliding starts, f has its maximum value μN, and 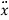 =0. The equations then give
=0. The equations then give
Wsinθmax = μN
Wcos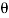 max = N
max = N
Hence
Tanθmax = μ
Notice that as the wedge angle is gradually increased from zero, the friction force grows in magnitude from zero toward its maximum value μN, since before the block begins to slide we have
f = Wsinθ θ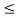 θmax
θmax
13 Question: Convert the rectangular coordinates (1,−3,5) to cylindrical coordinates?
Solution:
Use the second set of equations from Note to translate from rectangular to cylindrical coordinates:
r2=x2+y2
r = ±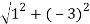 = ±
= ±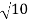
We choose the positive square root, so r = 
Now, we apply the formula to find θ. In this case, y is negative and x is positive, which means we must select the value of θ between 3π/2 and 2π
Tanθ= y/x = -3/1 =- 3
θ =arctan(−3) ≈5.03rad.
In this case, the z-coordinates are the same in both rectangular and cylindrical coordinates:
z=5.
The point with rectangular coordinates (1,−3,5) has cylindrical coordinates approximately equal to (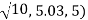 .
.
14 Question: A block of Mass M is moving with a velocity v on straight surface. What is the shortest distance and shortest time in which the block can be stopped if μ is coefficient of friction
a. v2/2μg,v/μg
b. v2/μg,v/μg
c. v2/2Mg,v/μg
d none of the above
Solution:
Force of friction opposes the motion
Force of friction=μN=μmg
Therefore retardation =μmg/m=μg
From v2=u2+2as
or
s=v2/2μg
from v=u+at
or t=v/μg
UNIT 1
INTRODUCTION TO MECHANICS
1Question: Discuss the fundamental forces in nature?
Solution:
A fundamental force of nature is an attraction or repulsion between objects as described through interactions between fields and particles.
Physics has identified four basic types of these interactions, which together describe every action we see in the Universe, from the decay of atomic particles to the drift of entire galaxies.
From walking on the street, to launching a rocket into space, to sticking a magnet on your refrigerator, physical forces are acting all around us. But all the forces that we experience every day (and many that we don't realize we experience every day) can be whittled down to just four fundamental forces:
- Electromagnetic Force
- Gravitational Force
- Strong Nuclear Force
- Weak Nuclear Force
These are called the four fundamental forces of nature, and they govern everything that happens in the universe.
- Electromagnetic Force
This is the second strongest force after the strong force and it acts on electrically charged particles. It has strength of 1/137 relative to the strong force but has an infinite range. However, this force has both attractive and repulsive properties due to the two charges it possesses; negative and positive. Objects of like charge will have a repulsive effect on each other, while objects of unlike charges will have an attractive effect and this can be demonstrated with a simple magnet or electric charges.
This is the force that's most obvious in our day-to-day lives. Thanks to the interactions of negatively-charged electrons and positively-charged protons, it allows single atoms to combine into different materials. The force is also carried through the electromagnetic field by a particle called a photon, which thanks to chemical changes in our eyes our bodies sense as light.
For the sake of convenience, we distinguish the two different kinds of charges by associating an algebraic sign with q, and for this reason we talk about negative and positive charges. The electrostatic force Fb on charge qb due to charge qa is given by Coulomb's law: k is a constant of proportionality and rab is a unit vector which points from a to b. If qa and qb are both negative or both positive, the force is repulsive, but if the charges are of different sign, Fb is attractive.
 = -
= - 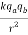

In the SI system, the unit of charge is the coulomb, abbreviated C. (The coulomb is defined in terms of electric currents and magnetic forces.) In this system, k is found by experiment to be
k = 8.99 x 109 N·m2/C2
2. Gravitational Force
This force is the weakest but has an infinite range. It has strength of 6 × 10-39 in comparison to the strength of the strong force. This force is always attractive acts between any two pieces of matter in nature. The effect of this gravitational force is dependent upon the mass of the two bodies and the distance between them.
Gravity is an attractive force between masses, which according to general relativity occurs as a result of the effect of energy acting on a space-time field. While theory suggests it could have a mediating particle - called a graviton - experiments are yet to support its existence.
While gravity might appear to be a strong force, responsible for holding entire galaxies together and squeezing the literal daylight out of stars, it's approximately 1029 times weaker than the weak nuclear force. That means it has virtually no observable effect on the scale of tiny particles, becoming relevant only on a more cosmic level.
Consider two particles, a and b, with masses Ma and Mb, respectively, separated by distance r. Let Fb be the force exerted on particle b by particle a.
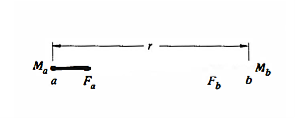
Figure 1
Our verbal description of the magnitude of the force is summarized by
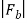 =
= 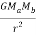
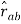
G is a constant of proportionality called the gravitational constant. Its value is found by measuring the force between masses in a known geometry. The first measurements were performed by Henry Cavendish in 1771 using a torsion balance.
The modern value of G is 6.67 X 10-11 N·m2/kg2. (G is the least accurately known of the fundamental constants. Perhaps you can devise a new way to measure it more precisely.) Experimentally, G is the same for all materials-aluminum, lead, neutrons, or what have you. For this reason, the law is called the universal law of gravitation.
3. Strong Nuclear Force
The strong nuclear force is what holds together the nuclei of atoms. This force holds the nucleus of an atom together. It is the strongest of the forces, but it is very short ranged. It acts over a range of about 10-15m, which is the average diameter of a medium sized nucleus. This force is attractive.
The protons and neutrons making up an atom's nucleus are themselves made up of a trio of simpler particles called quarks. A particle called a gluon acts on a property of quarks called colour, creating the force's pull.
Unlike the other three fundamental forces, the further the gluon needs to travel, the stronger the nuclear force gets. On the scale of protons and neutrons, this spring-like effect makes it incredibly hard to pull quarks apart. This helps explain why the strong force is so, well, strong.
On a scale of an atom's entire nucleus, the force also binds whole protons and neutrons to each other. Protons also push each other away thanks to the electromagnetic force, putting atomic nuclei into a delicate balance.
4. Weak Nuclear Force
This force is weak compared to the strong force as the name implies and has the shortest range of 10-18m, which is 0.1% of the diameter of a proton. It is responsible for radioactive decay especially nuclear beta decay. All particles experience this force.
Of all the fundamental forces, the weak nuclear force is the trickiest to grasp. It describes how the quarks that make up nuclear particles can change from one form into another. The force is carried by particles called W and Z bosons.
The weak force acts over an incredibly short distance, equal to about 0.1 percent of the diameter of a proton. When a particle such as a neutrino comes right up close to a quark, the weak force causes the quark to change by sending out a W boson. This can turn a neutron into a proton (creating a whole new element in the process), and the neutrino into an electron.
So We have studied that every pair of particles in the universe had its own special interaction, the task would be impossible. Fortunately, nature is kinder than this. As far as we know, there are only four fundamentally different types of interactions in the universe: gravity, electromagnetic interactions, the so-called weak interaction, and the strong interaction. Gravity and the electromagnetic interactions can act over a long range because they decrease only as the inverse square of the distance. However, the gravitational force always attracts, whereas electrical forces can either attract or repel. In large systems, electrical attraction and repulsion cancel to a high degree, and gravity alone is left. For this reason, gravitational forces dominate the cosmic scale of our universe. In contrast, the world immediately around us is dominated by the electrical forces, since they are far stronger than gravity on the atomic scale. Electrical forces are responsible for the structure of atoms, molecules, and more complex forms of matter, as well as the existence of light. The weak and strong interactions have such short ranges that they are important only at nuclear distances, typically 10-16 m.
They are negligible even at atomic distances, 10-10 m. As its name implies, the strong interaction is very strong, much stronger than the electromagnetic force at nuclear distances. It is the "glue" that binds the atomic nucleus, but aside from this it has little effect in the everyday world. The weak interaction plays a less dramatic role; it mediates in the creation and destruction of neutrinos-particles of no mass and no charge which are essential to our understanding of matter but which can be detected only by the most arduous experiments. Our object in the remainder of the chapter is to become familiar with the forces which are important in everyday mechanics. Two of these, the forces of gravity and electricity, are fundamental and cannot be explained in simpler terms. The other forces we shall discuss, friction, the contact force, and the viscous force, can be understood as the macroscopic manifestation of interatomic forces.
2 Question: Discuss the transformation of scalars and vectors under rotation transformation?
Solution:
Certain physical quantities such as mass or the absolute temperature at some point in space only have magnitude. A single number can represent each of these quantities, with appropriate units, which are called scalar quantities. There are, however, other physical quantities that have both magnitude and direction. Force is an example of a quantity that has both direction and magnitude (strength). Three numbers are needed to represent the magnitude and direction of a vector quantity in a three dimensional space. These quantities are called vector quantities.
Vector quantities also satisfy two distinct operations, vector addition and multiplication of a vector by a scalar. We can add two forces together and the sum of the forces must satisfy the rule for vector addition. We can multiply a force by a scalar thus increasing or decreasing its strength. Position, displacement, velocity, acceleration, force, and momentum are all physical quantities that can be represented mathematically by vectors. The set of vectors and the two operations form what is called a vector space. There are many types of vector spaces but we shall restrict our attention to the very familiar type of vector space in three dimensions that most students have encountered in their mathematical courses.
Vectors are sets of three quantities that transform in the same manner as the coordinates of a point P.
- Having a magnitude and direction is not sufficient to define a vector.
- Some transformations cannot be written in terms of a series of rotations. An example is an inversion. These are called improper rotations.
- Transformations that can be written in terms of a series of rotations are called proper rotations.
The laws of Physics are invariant'' under rotations of the coordinate system.
Rotational symmetry of laws of Physics implies conservation of Angular Momentum.
We will work with Passive Rotations'' where we rotate the coordinate axes rather than active rotations'' where we rotate the physical system and keep the axes fixed. These are essentially the same thing except the rotation angle changes sign.
A vector is a mathematical object that transforms in a particular way under rotations.
We know there are also physical quantities called scalars that are invariant under rotations.
Very often in practical problems, the components of a vector are known in one coordinate system but it is necessary to find them in some other coordinate system.
The relationship between the components in one coordinate system and the components in a second coordinate system are called the transformation equations. Any change of Cartesian coordinate system will be due to a translation of the base vectors and a rotation of the base vectors. A translation of the base vectors does not change the components of a vector.
Rotation of object relative to FIXED axis:
Basic equations you can get by looking at the diagram above:
x1= rcosα…………(1)
x2=rcos(θ+α)…………(2)
y1=rsinα…………(3)
y2=rsin(θ+α)…………(4)
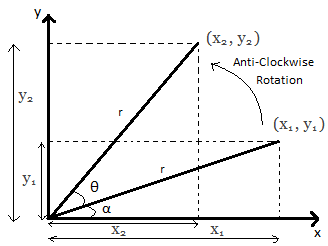
Figure: 1
Using trigonometric results the equations (2) and (4) become
x2=rcos(θ+α)
=rcosθcosα–rsinθsinα
=(rcosα)cosθ–(rsinα)sinθ
=x1cosθ–y1sinθ…………(5)
y2=rsin(θ+α)
=rsinθcosα+rcosθsinα
=(rcosα)cosθ+(rsinα)cosθ
=x1sinθ+y1cosθ…………(6)
Hence, For an anti-clockwise rotation,
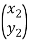 =
= 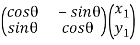 …………(7)
…………(7)
Is called the rotation matrix. Its determinant is 1.
To find the clockwise rotation matrix, you can do the calculations again. OR you can just transpose the above matrix OR you can substitute −θ into the matrix.
Hence, the clockwise rotation matrix is: 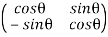
Note: Since clockwise rotation means rotating in the anti-clockwise direction by −θ, you can just substitute −θ into the anti-clockwise matrix to get the clockwise matrix. Since cos is an even function, it will not be affected by the −θ. (- cos x = cos x)
Rotation of coordinate axes:
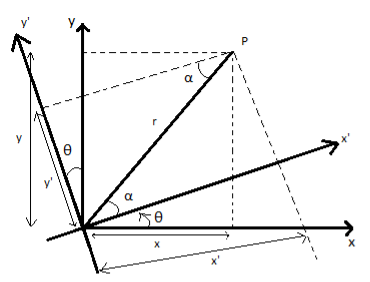
Figure: 2
Basic equations:
x′=rcosα…………(8)
x=rcos(θ+α) …………(9)
y′=rsin…………(10)
y=rsin(θ+α) …………(11)
Using trigonometric results the equations (9) and (11) become
x=rcos(θ+α)
=rcosθcosα–rsinθsinα
=x′cosθ–y′sinθ…………(12)
y=rsin(θ+α)
=rsinθcosα+rcosθsinα
=x′sinθ+y′cosθ…………(13)
From equation (13) So we have
x′= 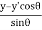 …………(14)
…………(14)
y′=  …………(15)
…………(15)
Substitute the above (14) and (15) equations into equation (12) and you will get:
y′=−xsinθ+ycosθ
x′=xcosθ+ysinθ
Hence,
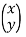 =
= 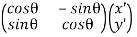 …………(16)
…………(16)
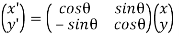 …………(17)
…………(17)
3 Question: State Newton’s first law of motion? Discuss it by giving some example?
Solution:
How do the forces that act on a body affect its motion? To begin to answer this question, let’s first consider what happens when the net force on a body is zero. You would almost certainly agree that if a body is at rest, and if no net force acts on it (that is, no net push or pull), that body will remain at rest. But what if there is zero net force acting on a body in motion? To see what happens in this case, suppose you slide a hockey puck along a horizontal table top, applying a horizontal force to it with your hand (Figure 2).
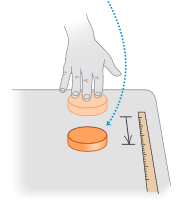
Figure 2: Table: puck stops short
After you stop pushing, the puck does not continue to move indefinitely; it slows down and stops. To keep it moving, you have to keep pushing (that is, applying a force). You might come to the “common sense” conclusion that bodies in motion naturally come to rest and that a force is required to sustain motion.
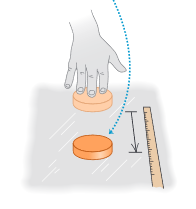
Figure 3: Table: Ice: puck slides farther
But now imagine pushing the puck across a smooth surface of ice (Figure 3). After you quit pushing, the puck will slide a lot farther before it stops. Put it on an air-hockey table, where it floats on a thin cushion of air, and it moves still farther (Figure 4).
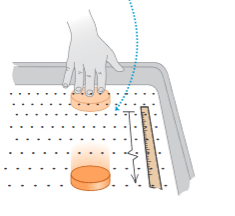
Figure 4: Air-hockey table: puck slides even farther
In each case, what slows the puck down is friction, an inter-action between the lower surface of the puck and the surface on which it slides. Each surface exerts a friction force on the puck that resists the puck’s motion; the difference in the three cases is the magnitude of the friction force. The ice exerts less friction than the table top, so the puck travels farther. The gas molecules of the air-hockey table exert the least friction of all.
If we could eliminate friction completely, the puck would never slow down, and we would need no force at all to keep the puck moving once it had been started. Thus the “common sense” idea that a force is required to sustain motion is incorrect. Experiments like the ones we’ve just described show that when no net force acts on a body, the body either remains at rest or moves with constant velocity in a straight line. Once a body has been set in motion, no net force is needed to keep it moving. We call this observation Newton’s first law of motion.
Newton’s First law can also be written as
A body acted on by no net force has a constant velocity (which may be zero) and zero acceleration
The tendency of a body to keep moving once it is set in motion is called inertia.
It’s important to note that the net force is what matters in Newton’s first law
Example
Suppose a hockey puck rests on a horizontal surface with negligible friction, such as an air-hockey table or a slab of wet ice.

Figure 5: (a) A hockey puck accelerates in the direction of a net applied force 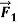 . (b) When the net force is zero, the acceleration is zero, and the puck is in equilibrium.
. (b) When the net force is zero, the acceleration is zero, and the puck is in equilibrium.
If the puck is initially at rest and a single horizontal force 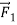 acts on it (Figure 5a), the puck starts to move. If the puck is in motion to begin with, the force changes its speed, its direction, or both, depending on the direction of the force. In this case the net force is equal to
acts on it (Figure 5a), the puck starts to move. If the puck is in motion to begin with, the force changes its speed, its direction, or both, depending on the direction of the force. In this case the net force is equal to  which is not zero. (There are also two vertical forces: the earth’s gravitational attraction and the upward normal force exerted by the surface. But as we mentioned earlier, these two forces cancel.)
which is not zero. (There are also two vertical forces: the earth’s gravitational attraction and the upward normal force exerted by the surface. But as we mentioned earlier, these two forces cancel.)
Now suppose we apply a second force, 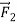 (Figure 5b), equal in magnitude to
(Figure 5b), equal in magnitude to 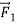 but opposite in direction. The two forces are negatives of each other,
but opposite in direction. The two forces are negatives of each other,
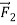
 ,and their vector sum is zero
,and their vector sum is zero
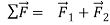
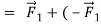

Again, we find that if the body is at rest at the start, it remains at rest; if it is initially moving, it continues to move in the same direction with constant speed. These results show that in Newton’s first law, zero net force is equivalent to no force at all. This is just the principle of superposition of forces.
When a body is either at rest or moving with constant velocity (in a straight line with constant speed), we say that the body is in equilibrium. For a body to be in equilibrium, it must be acted on by no forces, or by several forces such that their vector sum that is, the net force is zero.
4 Question: Derive Newton’s equations of motion in polar coordinates?
Solution:
Although Newton’s 2nd law takes a simple form in Cartesian coordinates, there are many circumstances where the symmetry of the problem lends itself to other coordinates.
To illustrate this, let’s take a look at 2-d polar coordinates. You should already have some familiarity with these, but we will see that certain complexities arise that require a bit of care.
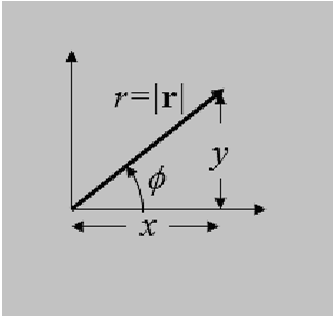
Figure 9
First of all you can go back and forth between Cartesian and polar coordinates by the familiar
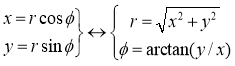
We now wish to introduce unit vectors for these new polar coordinates, (r, ϕ), which we will write  . Remember, these have to be 1 unit long, and point in the direction of r and ϕ.
. Remember, these have to be 1 unit long, and point in the direction of r and ϕ.
One way to construct a unit vector is to take any vector r and divide by its length |r|. Clearly, such a unit vector is in the direction of r but has unit length.
There is a major difference between the behavior of the cartesian unit vectors and the corresponding ones for polar coordinates.

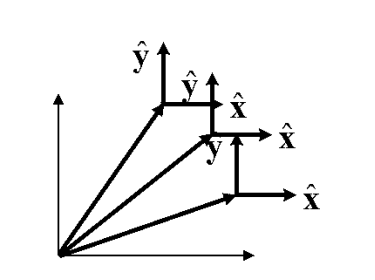
Figure 10: Cartesian unit vectors are constant
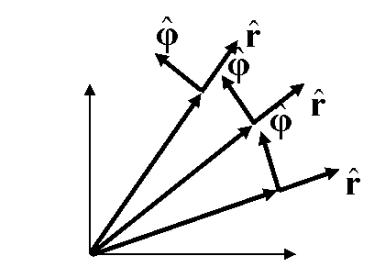
Figure 11: Polar coordinate unit vectors change (direction) with time
 Since
Since 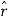 and
and 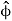 are perpendicular vectors in our two-dimensional space, any vector can be split into components in terms of them. For instance, the force F can be written:
are perpendicular vectors in our two-dimensional space, any vector can be split into components in terms of them. For instance, the force F can be written:
Imagine twirling a stone at the end of a string. Then the force Fr on the stone is just the tension in the string, and Fϕ might be the force of air resistance as the stone flies through the air.
The position vector is then particularly simple: r =r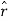
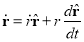 But to solve Newton’s 2nd law, F =m
But to solve Newton’s 2nd law, F =m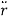 , we need the second derivative of r. Let’s just take the derivative using the product rule:
, we need the second derivative of r. Let’s just take the derivative using the product rule:
Where we keep the second term because now the unit vector 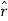 is not constant.
is not constant.
To see what the derivative of the unit vector is, let’s look at how 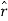 changes.
changes.
As the coordinate r changes from time t1 to time t2= t1 + Dt, the unit vector changes by:
We know that arc length = rθ
In this case, θ = 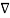 ϕ and r =
ϕ and r = 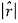 =1
=1
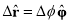

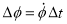 We can rewrite
We can rewrite
Hence
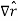 =
= 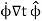
Or, after taking the limit as 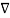 t approaches zero, we have
t approaches zero, we have
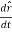 =
=
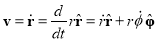 Thus, our first derivative is
Thus, our first derivative is
So the components of v are

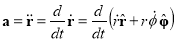 Now we need to take another derivative to get
Now we need to take another derivative to get
This is going to involve a time derivative of the 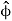 unit vector, for which we use much the same procedure as before.
unit vector, for which we use much the same procedure as before.
Since the 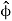 unit vector is perpendicular to the
unit vector is perpendicular to the 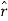 unit vector, we have the same geometry as before, except rotated 90 degrees.
unit vector, we have the same geometry as before, except rotated 90 degrees.
The change 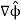 is now in the
is now in the 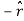 direction, and its length is again
direction, and its length is again
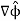
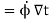 ,
,
So finally we have:
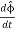 =
=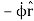
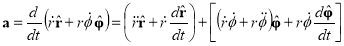 All that remains is to do a careful, term-by-term derivative to get
All that remains is to do a careful, term-by-term derivative to get
And then plug in our new-found expressions for the derivatives of the unit vectors.
And our expressions for the unit vector derivatives:
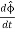 =
=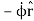
 =
=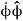
We have finally:

 Now that we have the acceleration, we are ready to write down Newton’s 2nd law in polar coordinates.
Now that we have the acceleration, we are ready to write down Newton’s 2nd law in polar coordinates.
This is the required result.
5 Question: State Newton’s second law of motion? Discuss it by giving some example?
Solution:
Newton’s first law tells us that when a body is acted on by zero net force, the body moves with constant velocity and zero acceleration. In Figure 6(a), a hockey puck is sliding to the right on wet ice. There is negligible friction, so there are no horizontal forces acting on the puck; the downward force of gravity and the upward normal force exerted by the ice surface sum to zero. So the net force 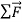 acting on the puck is zero, the puck has zero acceleration, and its velocity is constant.
acting on the puck is zero, the puck has zero acceleration, and its velocity is constant.
But what happens when the net force is not zero?
In Figure 6 (b) we apply a constant horizontal force to a sliding puck in the same direction that the puck is moving. Then 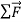 is constant and in the same horizontal direction as
is constant and in the same horizontal direction as 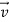 . We find that during the time the force is acting, the velocity of the puck changes at a constant rate; that is, the puck moves with constant acceleration. The speed of the puck increases, so the acceleration
. We find that during the time the force is acting, the velocity of the puck changes at a constant rate; that is, the puck moves with constant acceleration. The speed of the puck increases, so the acceleration 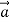 is in the same direction as
is in the same direction as 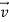 and
and 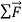 .
.
In Figure 6(c) we reverse the direction of the force on the puck so that 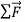 acts opposite to
acts opposite to  . In this case as well, the puck has acceleration; the puck moves more and more slowly to the right. The acceleration
. In this case as well, the puck has acceleration; the puck moves more and more slowly to the right. The acceleration 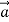 in this case is to the left, in the same direction as
in this case is to the left, in the same direction as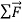 . As in the previous case, experiment shows that the acceleration is constant if
. As in the previous case, experiment shows that the acceleration is constant if 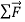 is constant. We conclude that net force acting on a body causes the body to accelerate in the same direction as the net force. If the magnitude of the net force is constant, as in Figures 6(b) and 6(c), then so is the magnitude of the acceleration.
is constant. We conclude that net force acting on a body causes the body to accelerate in the same direction as the net force. If the magnitude of the net force is constant, as in Figures 6(b) and 6(c), then so is the magnitude of the acceleration.
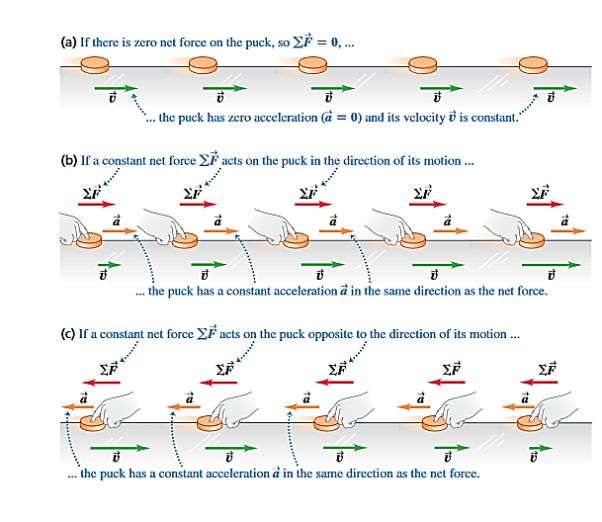
Figure 6: Using a hockey puck on a friction-less surface to explore the relationship between the net force 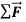 on a body and the resulting acceleration
on a body and the resulting acceleration 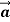 of the body.
of the body.
Our results mean that for a given body, the ratio of the magnitude  of the net force to the magnitude a=
of the net force to the magnitude a= 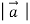 of the acceleration is constant, regardless of the magnitude of the net force. We call this ratio the inertial mass, or simply the mass, of the body and denote it by m. That is,
of the acceleration is constant, regardless of the magnitude of the net force. We call this ratio the inertial mass, or simply the mass, of the body and denote it by m. That is,
m=  or
or 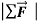 =ma or a=
=ma or a= 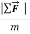
Mass is a quantitative measure of inertia. The above equations says that the greater a body’s mass, the more the body “resists” being accelerated. When you hold a piece of fruit in your hand at the supermarket and move it slightly up and down to estimate its heft, you’re applying a force and seeing how much the fruit accelerates up and down in response. If a force causes a large acceleration, the fruit has a small mass; if the same force causes only a small acceleration, the fruit has a large mass.
One newton is the amount of net force that gives an acceleration of 1 meter per second squared to a body with a mass of 1 kilogram.
For the same net force, the ratio of the masses of two bodies is the inverse of the ratio of their accelerations.
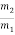 =
= 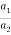 So Newton’s second law States that
So Newton’s second law States that
If a net external force acts on a body, the body accelerates. The direction of acceleration is the same as the direction of the net force. The mass of the body times the acceleration vector of the body equals the net force vector
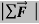 =ma
=ma
Newton’s second law is a fundamental law of nature, the basic relationship be-tween force and motion.
The statement of Newton’s second law refers to external forces. It’s impossible for a body to affect its own motion by exerting a force on itself; if it were possible, you could lift yourself to the ceiling by pulling up on your belt. That’s why only external forces are included in the sum 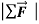 .
.
The design of high-performance motorcycles depends fundamentally on Newton’s second law. To maximize the forward acceleration, the designer makes the motorcycle as light as possible (that is, minimizes the mass) and uses the most powerful engine possible (thus maximizing the forward force).Light weight body (small m)Powerful engine (large F)application Blame Newton’s Second Law.
The above equations are valid only when the mass m is constant. It ’s easy to think of systems whose masses change, such as a leaking tank truck, a rocket ship, or a moving railroad car being loaded with coal. Such systems are better handled by using the concept of momentum.
Finally, Newton’s second law is valid in inertial frames of reference only, just like the first law. Thus it is not valid in the reference frame of any of the accelerating vehicles relative to any of these frames; the passenger accelerates even though the net force on the passenger is zero. We will usually assume that the earth is an adequate approximation to an inertial frame, although because of its rotation and orbital motion it is not precisely inertial.
Here is something important to discuss that m is not a force even though the vector m
is not a force even though the vector m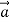 is equal to the vector sum
is equal to the vector sum  of all the forces acting on the body, the vector m
of all the forces acting on the body, the vector m is not a force. Acceleration is a result of a nonzero net force; it is not a force itself. It’s “common sense” to think that there is a “force of acceleration” that pushes you back into your seat when your car accelerates forward from rest. But there is no such force; instead, your inertia causes you to tend to stay at rest relative to the earth, and the car accelerates around you, The “common sense” confusion arises from trying to apply Newton’s second law where it isn’t valid—in the non-inertial reference frame of an accelerating car. We will always examine motion relative to inertial frames of reference only.
is not a force. Acceleration is a result of a nonzero net force; it is not a force itself. It’s “common sense” to think that there is a “force of acceleration” that pushes you back into your seat when your car accelerates forward from rest. But there is no such force; instead, your inertia causes you to tend to stay at rest relative to the earth, and the car accelerates around you, The “common sense” confusion arises from trying to apply Newton’s second law where it isn’t valid—in the non-inertial reference frame of an accelerating car. We will always examine motion relative to inertial frames of reference only.
6 Question: State Newton’s third law of motion? Discuss it by giving some example?
Solution:
Force acting on a body is always the result of its interaction with another body, so forces always come in pairs. You can’t pull on a doorknob without the door-knob pulling back on you. When you kick a football, the forward force that your foot exerts on the ball launches it into its trajectory, but you also feel the force the ball exerts back on your foot. In each of these cases, the force that you exert on the other body is in the opposite direction to the force that body exerts on you. Experiments show that whenever two bodies interact, the two forces that they exert on each other are always equal in magnitude and opposite in direction. This fact is called Newton’s third law of motion:
If body A exerts a force on body B (an “action”), then body B exerts a force on body A (a “reaction”). These two forces have the same magnitude but are opposite in direction. These two forces act on different bodies.
Or
To every action there is equal and opposite reaction.
For example, in Figure (7) 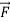 A on B is the force applied by body A (first sub-script) on body B (second subscript), and
A on B is the force applied by body A (first sub-script) on body B (second subscript), and 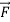 B on A is the force applied by body B(first subscript) on body A (second subscript).
B on A is the force applied by body B(first subscript) on body A (second subscript).

Figure 7: Newton’s third law of motion
In equation form,
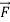 A on B =
A on B = 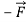 B on A
B on A
In the statement of Newton’s third law, “action” and “reaction” are the two opposite forces; we sometimes refer to them as an action–reaction pair. This is not meant to imply any cause-and-effect relation-ship; we can consider either force as the “action” and the other as the “reaction.” We often say simply that the forces are “equal and opposite,” meaning that they have equal magnitudes and opposite directions. The two forces in an action–reaction pair act on different bodies We stress that the two forces described in Newton’s third law act on different bodies.
The action and reaction forces are contact forces that are present only when the two bodies are touching. But Newton’s third law also applies to long-range forces that do not require physical contact, such as the force of gravitational attraction. A table-tennis ball exerts an upward gravitational force on the earth that’s equal in magnitude to the downward gravitational force the earth exerts on the ball. When you drop the ball, both the ball and the earth accelerate toward each other. The net force on each body has the same magnitude, but the earth’s acceleration is microscopically small because its mass is so great. Nevertheless, it does move.
7 Question: Prove that Newton’s second law of motion is invariant under transformation?
Solution:
Suppose there are two reference frames (systems) designated by S and S' such that the coordinate axes are parallel. In S, we have the co-ordinates {x,y,z,t} and in S' we have the co-ordinates {x’,y’,z’,t’}. S' is moving with respect to S with velocity v (as measured in S) in the x direction. The clocks in both systems were synchronised at time t=0 and they run at the same rate.
![\includegraphics[width=0.7\textwidth]{ref_frames.eps}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1650892698_3990486.png)
Figure 8 : Reference frame S' moves with velocity v (in the x direction) relative to reference frame S.
We have the intuitive relationships
x’ = x-vt
y’=y
z’=z
t’=t
This set of equations is known as the Galilean Transformation. They enable us to relate a measurement in one inertial reference frame to another. For example, suppose we measure the velocity of a vehicle moving in the in x-direction in system S, and we want to know what would be the velocity of the vehicle in S'.
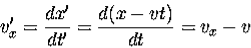 ………..(1)
………..(1)
This is the result our intuition is familiar with.
We have stated the we would like the laws of physics to be the same in all inertial reference frames, as this is indeed our experience of nature. Physically, we should be able to perform the same experiments in different reference frames, and find always the same physical laws. Mathematically, these laws are expressed by equations. So, we should be able to transform'' our equations from one inertial reference frame to the other inertial reference frame, and always find the same answer.
We will check that Newton's Second Law is the same in two different reference frames. We put one observer in the un-primed frame and the other in the primed frame, moving with velocity 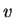 relative to the un-primed frame. Consider the vehicle of the previous case undergoing a constant acceleration in the x-direction,
relative to the un-primed frame. Consider the vehicle of the previous case undergoing a constant acceleration in the x-direction,
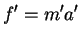

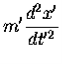

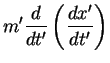



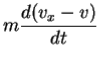
v is constant so we have

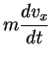

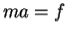
Indeed, it does not matter which inertial frame we observe from, we recover the same Second Law of Motion each time. We say the Second Law of Motion is invariant under the Galilean Transformation.
8 Question: Transform rectangular coordinates in spherical coordinates?
Solution:
Spherical coordinates are similar to the way we describe a point on the surface of the earth using latitude and longitude. By specifying the radius of a sphere and the latitude and longitude of a point on the surface of that sphere, we can describe any point in R3. To describe the latitude and longitude, we use two angles: θ (the angle from the positive x axis) and ϕ (the angle from the positive z axis). We therefore have three coordinates (ρ,θ,ϕ), where ρ is the radius of the sphere.
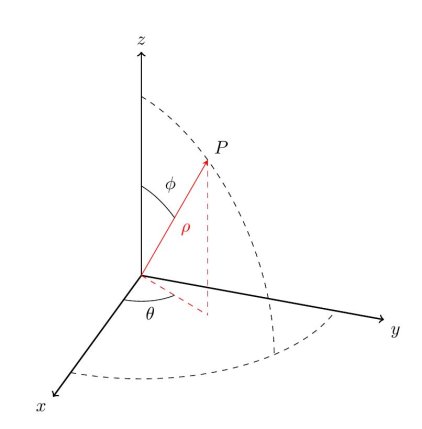
Figure 15
Where the first component is the distance from the origin to the point, the second component is the polar angle and the third component is the altitude angle measured from the positive z-axis to the line connecting the origin and the point.
Note that
0≤θ<2π
0≤ϕ≤π
ρ≥0
The formulas that we need in order to convert between rectangular and spherical coordinates are given below, without derivation
ρ=x2+y2+z2
x=ρcosθsinϕ
y=ρsinθsinϕ
z=ρcosϕ
9 Question: Convert (3, π/4, 4) in cylindrical coordinates to rectangular coordinates.
Solution:
Use the formulas, noting that r=3, θ=π/4, and z=4.
x=rcosθ=3cosπ/4= 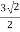
y=rsinθ=3sinπ/4= 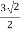
z=4
Therefore point is (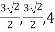 ) in rectangular coordinates.
) in rectangular coordinates.
To go in the other direction (from rectangular coordinates to cylindrical), use the following set of formulas (again, the first two are exactly what we use to convert from rectangular to polar in R2:
r=x2+y2
θ=tan−1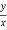
z=z
10 Question: Plot the point with spherical coordinates (8, π/3, π/6) and express its location in both rectangular and cylindrical coordinates.
Solution:
Use the equations in Note to translate between spherical and cylindrical coordinates
ρ=x2+y2+z2
x=ρcosθsinϕ = 8sin(π/6)cos(π/3) = 8(1/2)1/2=2
y=ρsinθsinϕ =8sin(π/6)sin(π/3)=8(1/2)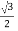 =2
=2
z=ρcosϕ =ρcosφ =8cos(π/6)= 8(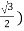 =4
=4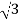
The point with spherical coordinates (8,π/3,π/6) has rectangular coordinates (2, 2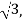 4
4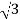 )
)
Finding the values in cylindrical coordinates is equally straightforward:
r=ρsinφ=8sinπ/6= 4
θ= θ
z=ρcosφ=8cosπ/6= 4
Thus, cylindrical coordinates for the point are (4,π/3, 4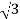 )
)
.
11 Question: Define Friction
Solution:
Friction cannot be described by a simple formula, but macroscopic mechanics is hard to understand without some idea of the properties of friction. Friction arises when the surface of one body moves, or tries to move, along the surface of a second body. The magnitude of the force of friction varies in a complicated way with the nature of the surfaces and their relative velocity. In fact, the only thing we can always say about friction is that it opposes the motion which would occur in its absence.
For instance, suppose that we try to push a book across a table. If we push gently, the book remains at rest; the force of friction assumes a value equal and opposite to the tangential force we apply. In this case, the force of friction assumes whatever value is needed to keep the book at rest. However, the friction force cannot increase indefinitely. If we push hard enough, the book starts to slide. For many surfaces the maximum value of the friction is found to be equal to μN, where N is the normal force and μ is the coefficient of friction. When a body slides across a surface, the friction force is directed opposite to the instantaneous velocity and has magnitude μN.
For two given surfaces the force of sliding friction is essentially independent of the area of contact.
12 Question: A block of mass m rests on a fixed wedge of angle θ. The coefficient of friction is μ. (For wooden blocks, μ is of the order of 0.2 to 0.5.) Find the value of θ at which the block starts to slide?
Solution:
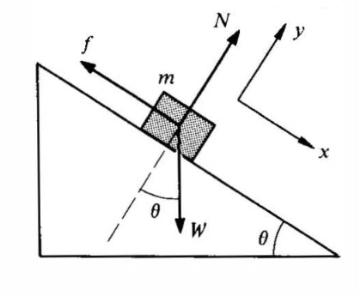
Figure 12
In the absence of friction, the block would slide down the plane; hence the friction force f Points up the plane. With the coordinates shown, we have
m = Wsinθ – f
= Wsinθ – f
And
m = N -Wcos
= N -Wcos = 0.
= 0.
When sliding starts, f has its maximum value μN, and 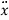 =0. The equations then give
=0. The equations then give
Wsinθmax = μN
Wcos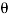 max = N
max = N
Hence
Tanθmax = μ
Notice that as the wedge angle is gradually increased from zero, the friction force grows in magnitude from zero toward its maximum value μN, since before the block begins to slide we have
f = Wsinθ θ θmax
θmax
13 Question: Convert the rectangular coordinates (1,−3,5) to cylindrical coordinates?
Solution:
Use the second set of equations from Note to translate from rectangular to cylindrical coordinates:
r2=x2+y2
r = ±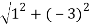 = ±
= ±
We choose the positive square root, so r = 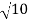
Now, we apply the formula to find θ. In this case, y is negative and x is positive, which means we must select the value of θ between 3π/2 and 2π
Tanθ= y/x = -3/1 =- 3
θ =arctan(−3) ≈5.03rad.
In this case, the z-coordinates are the same in both rectangular and cylindrical coordinates:
z=5.
The point with rectangular coordinates (1,−3,5) has cylindrical coordinates approximately equal to (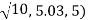 .
.
14 Question: A block of Mass M is moving with a velocity v on straight surface. What is the shortest distance and shortest time in which the block can be stopped if μ is coefficient of friction
a. v2/2μg,v/μg
b. v2/μg,v/μg
c. v2/2Mg,v/μg
d none of the above
Solution:
Force of friction opposes the motion
Force of friction=μN=μmg
Therefore retardation =μmg/m=μg
From v2=u2+2as
or
s=v2/2μg
from v=u+at
or t=v/μg