UNIT-1
INTRODUCTORY MECHANICS & THEORY OF RELATIVITY
QUESTION BANK
1 Question: Calculate the time interval of the signal using Lorentz transformation when a spacecraft S’ is crossed by another spacecraft S at a speed of c/2 on their way to Alpha Centauri. When spacecraft S crosses S’, the captain of S’ sends a signal that lasts for 1.2s.What is the fine time interval of the single.
Solution:
Given:
Δt’ = t‘2−t‘1 = 1.2s
Δx’ = x‘2−x‘1 = 0
The time signal starts and ends at (x’, t‘1)
Using the first Lorentz transformation equation we get,
Δt = t2 – t1
Δx = x2 – x1
Δt= 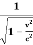 (
( 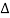 t’ +
t’ + 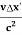 )
)
As the time interval of S’ is fixed, we can consider Δx’ = 0 and the time interval δt becomes:
Δt=
Substituting Δt’ = 1.2s we get
Δt=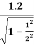
Δt = 1.6s
2 Question: A certain process requires 10-6 sec to occur in an atom at rest in laboratory. How much time will this process require to an observer in the laboratory? When the atom is moving with speed of 5 x107 m/sec.
Solution:
Given Δt = 10-6 sec
v = 5 x109 cm/sec
∆t= 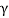 (∆t')
(∆t')
∆t' = ∆t /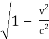
∆t' =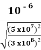 = 1.028 x10-6 sec
= 1.028 x10-6 sec
3 Question: Compute the contracted length of an object whose initial length 10m and travel with a velocity 0.75c?
Solution:
Given parameters are,
L0 = 10m
v = 0.75c
c = Speed of light (3.0 x 108 m/s)
The formula for length contraction is
l0 = 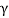 l
l
Or L0 = 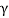 L
L
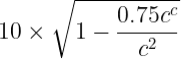
L = 10 × √1- (0.75)2
L = 10 × √(o.438)
L = 6.618 m.
4 Question: A observer on earth sees a rocket zoom by at .95c. If the rocket is measured to be 5.5 m in length, how long is the rocket ship as measure by the astronaut inside the rocket?
Solution:
The formula for length contraction is
l0 = 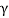 l
l
Or
L0 = 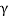 L
L
L = 5.5 m
v = .95c
L0 = ?
5.5 = L0×(1- 0.95c2/c2)
5.5 = L0×(0.312)
L0 = 5.5/(0.312) = 17.6 m
5 Question: Difference between inertial & non-inertial frames?
Solution:
Inertial frame of reference
An inertial frame is defined as one in which Newton’s law of inertia holds that is anybody which isn’t being acted on by an outside force stays at rest if it is initially at rest, or continues to move at a constant velocity if that’s what it was doing to begin with.
Non-inertial frame of reference
A frame that is accelerated with respect to the assumed inertial frame of reference. Newton’s law will not hold true in these frames.
6 Question: The Hypersonic Technology Vehicle 2 (HTV-2) is an experimental rocket vehicle capable of traveling at 21,000 km/h (5830 m/s). If an electronic clock in the HTV-2 measures a time interval of exactly 1-s duration, what would observers on Earth measure the time interval to be?
Solution:
Given
Δτ=1s
v=5830m/s.
Δt =?
We know ∆t= t1 – t2 = 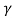 (∆t')
(∆t')
Δt=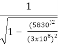 = 1.000000000189s
= 1.000000000189s
7 Question: What are Galilean Transformations? How velocity and acceleration transform?
Solution:
Galilean Coordinate Transformations: For simplicity: - Let coordinates in both references equal at (t = 0). Use Cartesian coordinate systems.
Newton’s laws are only applicable at inertial reference frames. According to Galilean transformations, Newton’s laws are invariant at any inertial reference frame. In other words, the mechanical movement of a particle is exactly the same at two different reference frames, If both of them are inertial (i.e. one moves with constant velocity w.r.t the other & vice versa).
There is no mechanical experiment by which one can distinguish whether a system is at rest or is moving with a constant speed in a straight line (Galilean relativity).
Suppose we know from experiment that these laws of mechanics are true in one frame of reference. How do they look in another frame, moving with respect to the first frame?
To find out, we have to figure out how to get from position, velocity and acceleration in one frame to the corresponding quantities in the second frame.
Obviously, the two frames must have a constant relative velocity, otherwise the law of inertia won’t hold in both of them. Let’s choose the coordinates so that this velocity is along the x-axis of both of them.
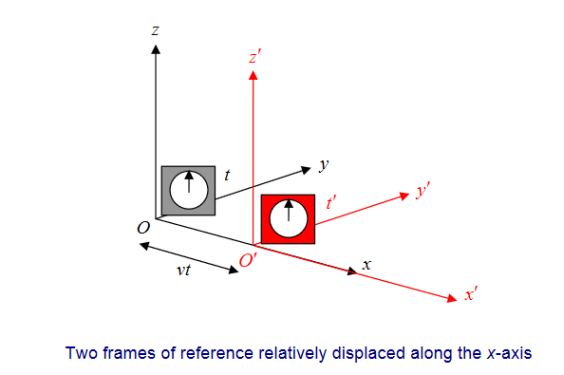
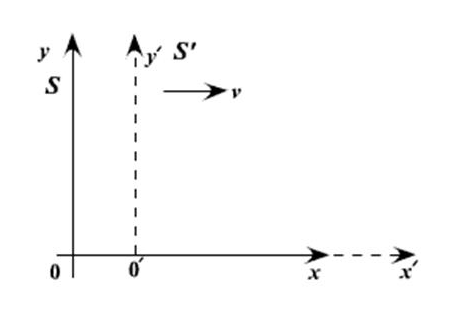
Notice we also throw in a clock with each frame. Suppose S′ is moving relative to S at speed v along the x-axis. For convenience, let us label the moment when O′ passes O as the zero point of timekeeping. That mean at t=0 O and O’ coincide with each other.
Now let us try to find the coordinates of the event (x, y, z, t) in S′
It’s easy to see t′ = t
We synchronized the clocks when O′ passed O. Also, evidently, y′ = y and z′ = z, from the figure.
We can also see that x = x′ +vt.
Thus (x, y, z, t) in S corresponds to (x′, y′, z′, t′) in S′, where
x = x′ +vt.
y = y’
z = z’
t =t’
That’s how positions transform; these are known as the Galilean Transformations.
- Velocity
The velocity in S′ in the x′ direction is given by u’x
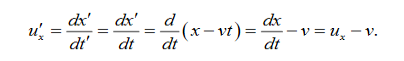
This is obvious anyway it’s just the addition of velocities formula.
ux = u’x +v
- Acceleration
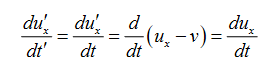
Since v is constant. That is to say,
a’x =ax
The acceleration is the same in both frames. This again is obvious as the acceleration is the rate of change of velocity, and the velocities of the same particle measured in the two frames differ by a constant factor-the relative velocity of the two frames.
8 Question: Explain construction, working and conclusion of Michelson Morley experiment?
Solution:
The experiment was devised to determine the absolute velocity of earth with respect to ether frame. The simplified plan of the experiment is shown in figure.
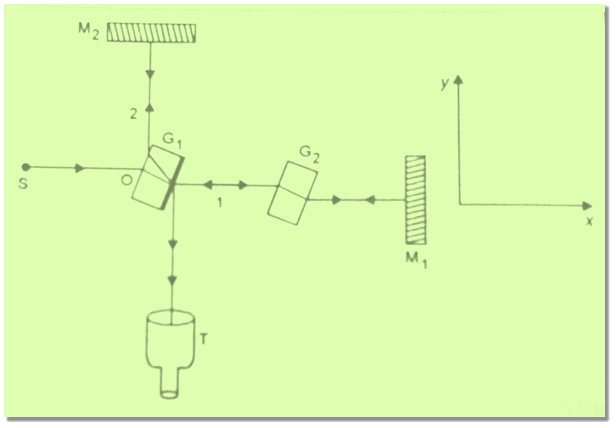
Figure: Michelson Morley Experiment
- Construction
Light from a source S falls on a glass plate G1 inclined at an angle of 45° to the incident beam. The back surface of the plate G1 is half silvered. This plate divides the incident beam into two beams 1 and 2 of equal intensity. The beam 1 (transmitted by the plate G1) goes straight to another glass plate G2 of the same thickness as G1 and inclined at an angle of 45° to the beam. This beam after crossing G2 falls normally on the plate mirror M1 and is reflected back towards glass plate G1. On reaching the back surface of G1 it again suffers 50% reflection. The reflected part enters the telescope T.
The beam 2 (reflected by the glass plate G1) moves towards the mirror M2, to fall normally on it. It retraces its path after reflection from M2. When it reaches the back surface of G1, it suffers 50% transmission. The transmitted part goes into the telescope and interferes with the reflected part of the beam 1. Interference fringes are therefore observed in the telescope.
Since the two glass plates G1 and G2 are identical then the path of the two beams are equal in glass. Each beam passes three times through a glass plate in its journey from the source to the telescope. If the mirrors M1 and M2 are at the same distance from 0, then the optical path lengths of two beams shall be equal say l.
- Working
We know that the earth moves around the sun with an orbital velocity of Since the earth is moving through ether with velocity v it experiences an ether wind of velocity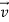 . Suppose the velocity of the earth is along positive x-direction. Let the apparatus be oriented in such a way that incident beam travels parallel to the velocity of earth. Then the velocity of beam is along positive x-axis. When this incident beam travels in the positive x direction, it faces an ether wind blowing in negative x direction.
. Suppose the velocity of the earth is along positive x-direction. Let the apparatus be oriented in such a way that incident beam travels parallel to the velocity of earth. Then the velocity of beam is along positive x-axis. When this incident beam travels in the positive x direction, it faces an ether wind blowing in negative x direction.
- Time for round trip of light beam 1 travelling in x direction.
When the beam 1 transmitted by G1 travels along the positive x direction from 0 to M1, its effective velocity v1 in earth’s frame is
v1 = c - v
Because the ether wind is opposed to the direction of motion of the beam. The time taken by the light to travel from 0 to M1 is
t1 = 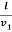 =
= 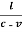
In the return journey from M1 to 0 the ether wind is supporting the beam of light. Therefore its effective velocity v2 in earth's frame is
v2 = c + v
The time taken by the light for its return journey M1O is
t2=  =
= 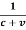
Thus the time of the round trip OM1O is
T1 = t1 + t2
T1 =  +
+ 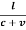 +
+ 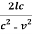
T1 = 2lc (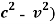 – 1 =
– 1 = 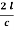 (1 -
(1 - 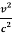 ) – 1
) – 1
Since  =
= 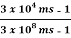 = 10-4<< 1
= 10-4<< 1
We can expand the above expression by Binomial theorem. This gives
T1 = 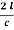 (1 -
(1 - 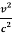 )
)
- Time for round trip of light beam 2 travelling in y direction.
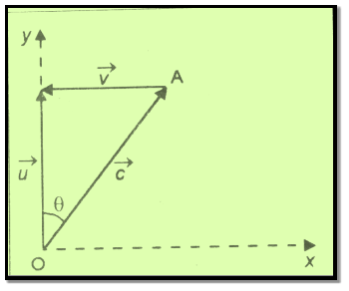
The beam 2 travels from O to the mirror M2 parallel to y direction. Since it to moving parallel to y direction its effective velocity must be in the y direction.
Suppose  is the effective velocity of beam 2 in y direction as shown in figure. The ether wind velocity is in the negative x direction and is shown by vector
is the effective velocity of beam 2 in y direction as shown in figure. The ether wind velocity is in the negative x direction and is shown by vector 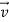 . Therefore the actual velocity of beam 2 should be in OA direction. From figure.
. Therefore the actual velocity of beam 2 should be in OA direction. From figure.
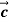 +
+  =
= 
 =
= 
The square of magnitude of  is
is
c2 = u2 + v2 – 2 u v cos 90°
c2 = u2 + v2
Or u2 = c2 - v2
u = 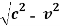
The effective velocity u of the beam is the same during its return journey from M2 to O. Thus time taken to travel from M2 to O is
t2' = t1' = 
Thus the time of round trip for the beam 2 is
T2 = 2t1' = 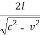
T2 = 2l (c2 – v2)-1/2 = 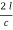 (1 -
(1 - 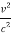 )-1/2
)-1/2
Since  << 1 we can expand by Binomial theorem. This gives
<< 1 we can expand by Binomial theorem. This gives
T2 =  ( 1 +
( 1 +  )
)
- Expected Fringe shift
The time difference between the two beams for their round trips is
T = T1 – T2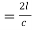 ( 1 +
( 1 + 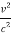 ) -
) - 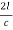 ( 1 +
( 1 + 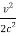 )
)
T= 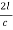 [( 1 +
[( 1 + 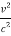 - 1 -
- 1 - 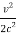 )]
)]
T= 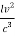
Thus the optical path difference  between two beams corresponding to the time difference T is
between two beams corresponding to the time difference T is
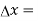 cT =
cT =
Now suppose this whole apparatus is turned through 90° so that the two beams interchange their paths. Thus path OM2, becomes parallel to the incident beam and OM1 becomes perpendicular to the incident beam. Then the two times T1 and T2 will interchange and the path difference between two beams changes from  to -
to - 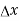 . Thus the path difference between two beams in the second position is
. Thus the path difference between two beams in the second position is
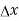 = -
= - 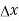 = -
= -
The change in the optical path difference between the two beams due to 90° rotation of the apparatus
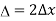 =
= 
This path difference should lead to the shift of fringes.
- Order of Fringe Shift
Suppose λ is the wavelength of light used. We know that a path difference of one wavelength λ corresponds to shift of one fringe across a cross wire in the field of view of telescope. If  n is the number of fringes which shift on turning the apparatus through 90° then
n is the number of fringes which shift on turning the apparatus through 90° then
 n =
n =
In Michelson Morely experiment the distance l= 11 meters,
λ = 5900Å = 5.9 x 10-7 m
v/c = 10-4. Thus
 n = 0 37
n = 0 37
Thus a fringe shift was expected in this experiment if the concept of the ether frame was valid. In actual experiment no fringe shift was observed.
- CONCLUSION
The negative result of Michelson Morley experiment led to the following conclusion.
The motion of earth through the ether could not to be detected experimentally. Thus the concept of a preferred ether frame must be discarded.
The speed of light in vacuum is same in all frames of reference which are in uniform relative motion.
This experiment paved the way for the development of the special theory of relativity by Einstein in the year 1905.
9 Question:What are conservative and non-conservative forces?
Solution:
A conservative force may be defined as one for which the work done in moving between two points A and B is independent of the path taken between the two points. The implication of "conservative" in this context is that you could move it from A to B by one path and return to A by another path with no net loss of energy - any closed return path to A takes net zero work.
A further implication is that the energy of an object which is subject only to that conservative force is dependent upon its position and not upon the path by which it reached that position. This makes it possible to define a potential energy function which depends upon position only.
A conservative force is a force that does zero work done in a closed path. If only these forces act then the mechanical energy of the system remains conserved. Examples of conservative force: Gravitational force, spring force etc.
On the other hand, non-conservative forces are those forces which cause loss of mechanical energy from the system. In the above case friction is the non-conservative force. But as we know energy can neither be created nor destroyed hence these forces convert mechanical energy into heat, sound, light etc.
Now, Conservative force has one more property that works done by it is independent of the path taken.
Forces are either conservative or non-conservative. Conservative forces we already discussed. A non-conservativeforce is one for which work depends on the path taken. Friction is a good example of a non-conservative force. As illustrated in Figure 11,
11 Figure
Work done against friction depends on the length of the path between the starting and ending points. Because of this dependence on path, there is no potential energy associated with non-conservative forces. An important characteristic is that the work done by a non-conservative force adds or removes mechanical energy from a system. Friction, for example, creates thermal energythat dissipates, removing energy from the system. Furthermore, even if the thermal energy is retained or captured, it cannot be fully converted back to work, so it is lost or not recoverable in that sense as well.
In Figure 11. The amount of the happy face erased depends on the path taken by the eraser between points A and B, as does the work done against friction. Less work is done and less of the face is erased for the path in (a) than for the path in (b). The force here is friction, and most of the work goes into thermal energy that subsequently leaves the system (the happy face plus the eraser). The energy expended cannot be fully recovered.
10 Question:Derive Lorentz Transformation equation?
Solution:
Lorentz transformation is the relationship between two different coordinate frames that move at a constant velocity and are relative to each other. The name of the transformation comes from a Dutch physicist Hendrik Lorentz.
The Galilean transformation nevertheless violates Einstein’s postulates, because the velocity equations state that a pulse of light moving with speed c along the x-axis would travel at speed c−v in the other inertial frame.
Specifically, the spherical pulse has radius r=ct at time t in the unprimed frame, and also has radius r′=ct′ at time t' in the primed frame.
Expressing these relations in Cartesian coordinates gives
x2+y2+z2−c2t2 =0………..(1)
x′2+y′2+z′2−c2t′2=0………..(2)
The left-hand sides Equations and can be set equal because both are zero.
Because y=y′ and z=z′ so, we obtain
x2−c2t2 =x′2−c2t′2………..(3)
However this cannot be satisfied for nonzero relative velocity v of the two frames if we assume the Galilean transformation results in t=t′ with x=x′+vt′.
To find the correct set of transformation equations, assume the two coordinate systems S and S′
The laws of mechanics are invariant under Galilean transformations, whereas electrodynamics and Maxwell’s equations are varying under this transformation. This shows that the velocity of light will have different values for different observers moving with different uniform velocities. But the speed of light is invariant in all inertial frames of reference; hence, Galilean transformations need to be modified.
Lorentz deduced the transformation equations, which are in agreement with the results of Michelson–Morley experiment. The Lorentz transformations are deduced as given below.
Lorentz transformation equations are developed. Let x, y, z and t be the space and time coordinate in rest system or standard system. The system with x', y', z' moves with velocity 'v' along the x-axis.
The origins at t=t'=0 coincide. The most general transformation equations relating the coordinates of an event in two systems can be written as,
x’ = Ax +Bt………..(4)
y’ = y………..(5)
z’ = z………..(6)
t’ = Cx +Dt………..(7)

The transformations are linear.
If they are not linear one system would predict acceleration while in other system velocity was even constant.
Because of symmetry, y' and z' axes are left unchanged by the transformation.
Constant can be calculated by using the following boundary conditions.
- Observers in S and S' see (O') the origin of S' as
x = vt
x’ = 0
Substituting values of x and x' in equation (4) We get
0 = Avt +Bt
i.e. B =- Av………..(8)
- Observer in S' and S see the origin (O) of S as
x' = vt
x = 0
Substituting values of x and x' in equation (4) we get
-vt’ =Bt………..(9)
Substituting the value of B from equation (8), we get
-vt’ =- Avt………..(10)
In equation (7) put x=0 we get
t’ = Dt
So equation (10) become
-v Dt =- Avt
A =D ………..(11)
- A light pulse is sent out from the origin of S towards x at t=0, its location is given by
x= ct
x’ = ct’
Substituting values of x and x' in equation (4), we get
Ct’ = Act +Bt
Substituting the value of B from equation (8), we get
Ct’ = Act +(- Avt) ………..(12)
Substituting values of x and D from eq no (11) in eq no.(7) , we get
t’ = Cct +At
Substituting above value of t' in eq no.(12) , we get
c(Cct +At) = Act - Avt
Or
Cc2t +Act =Act - Avt
Cc2t =Avt
Or
C =-A  ………..(13)
………..(13)
- A light pulse is emitted along y axis in S system at t=0, its coordinate in both systems are
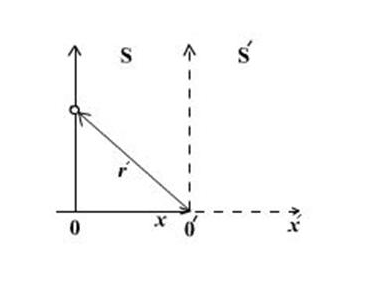
y= ct, x=0
r’=ct’ where
Using equation (5)
r’2 = x’2+y’2
Using equation (5)
y’= y= ct
And from equation (4) and (7)
x’ = Bt = -Avt
t’= Dt =-At
Therefore r’2 = x’2+y’2 become
c2t’2 = (-Avt)2 +(ct)2
Substituting value of t' above equation became
c2A2t2 = A2v2t2 +c2t2
(c2 - v2)A2t2 = c2t2
A2 = 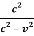
A = 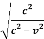
A = 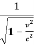 ………..(14)
………..(14)
Substituting the Values of A, B, C, D in equation (1) and (4)
So the Lorentz transformation equations would be,
x’=  -
-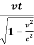
x’= 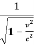 (x-vt)
(x-vt)
x’=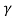 (x-vt)
(x-vt)
Where 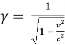
And
t’ = - 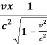 +
+ 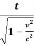
t’=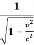 ( t -
( t - 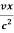 )
)
Lorentz transformation equations therefore are
x’= 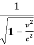 (x - vt)
(x - vt)
y’ =y
z’ = z
t’=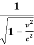 ( t -
( t -  )
)
Or these can be written as
x’= 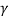 (x-vt)
(x-vt)
y’ =y
z’ = z
t’=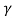 ( t -
( t - 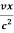 )
)
Where 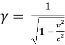
This set of equations, relating the position and time in the two inertial frames, is known as the Lorentz transformation. They are named in honour of H.A. Lorentz (1853–1928), who first proposed them. Interestingly, he justified the transformation on what was eventually discovered to be a fallacious hypothesis.
The reverse transformation expresses by the following equations. Simply interchanging the primed and unprimed variables and substituting gives:
x= 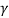 (x’+ vt)
(x’+ vt)
y =y’
z = z’
t= (t’ +
(t’ +  )
)
11 Question: What do you meant by length contraction?
Solution:
Consider a frame S' moving with respect to S with a uniform speed v along x direction figure. Let the rod AB lie along the O'x' axis. The rod is at rest in the frame S' and its length as measured by an observer in S' shall be called the rest length of the rod. To calculate this length the observer in S' will measure the x' coordinates of the two ends A and B. These coordinates shall be independent of the time of observation. If x1' and x2' are the x' coordinates of two ends A and B then the rest length l0 of the rod is
l0 = x'2 – x'1
In the coordinate system S the x coordinates of ends A and B will change with time. In order to measure the length of the rod, the observer in S will have to measure simultaneously the coordinates of the ends A and B. If x1 and x2 are the coordinates of ends A and B at the time of observation t then the length of rod as observed in frame S is
l= x2 – x1
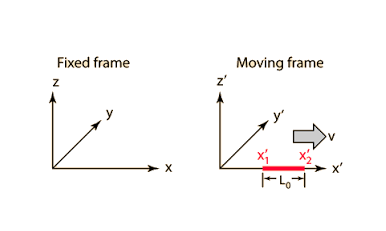
Figure: Length Contraction
From Lorentz equations we have
x'2 = 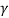 (x2 – v t)
(x2 – v t)
x1' = 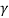 (x1 – v t)
(x1 – v t)
Subtracting these equations we obtain
x2' - x1' = 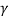 (x2 — x1)
(x2 — x1)
Using eq. (6.57) and (6.58) it becomes
l0 = 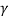 l
l
I = 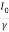
Since 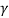 is always greater than one, therefore
is always greater than one, therefore
l<l0
Thus the length of the rod measured from the frame in which it is moving is smaller than its length in a frame in which it is at rest by a factor  or
or  Hence the length of a moving rod appears shortened by a factor
Hence the length of a moving rod appears shortened by a factor 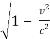
Note the following points
- The length contraction is significant only if the speed of rod approaches the velocity of light.
- The shortening of rod occurs only along the line of motion. The length of meter stick oriented perpendicular to the direction of motion is not changed.
12 Question: What do you meant by time dilation?
Solution:
Consider a frame S' moving with velocity v with respect to frame S along the x direction Fig (6.6). Suppose the clock is located in the system S' at the point x'. The clock is stationary with respect to S'. Let t1 ' and t2' are two instants of time recorded on this clock by an observer in S'. Then the interval of time as observed in S' is
∆t' = t2' – t1'
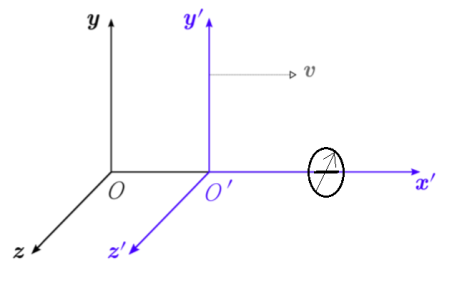
Figure: Time dilation
Now we wish to find how this time interval appears to an observer in S. This can be done by applying a Lorentz transformation from S' to S with the same value of x'. The transformation equation required is (6.51 d). From this we can write
t1 =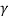 (t1' + v x' / c2)
(t1' + v x' / c2)
t2 = 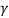 (t'2 + v x' / c2)
(t'2 + v x' / c2)
Subtracting eq. (6.64) from eq. (6.63) we obtain
∆t= t1 – t2 = 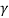 (t1' – t2')
(t1' – t2')
Using eq. (6.62) it becomes
∆t= t1 – t2 = 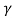 (∆t')
(∆t')
Since 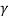 > 1 so
> 1 so
∆t > ∆t'
This means that the time interval as observed in the moving frame of clock is greater than the One observed in the rest frame of the clock. We can express the same thing by saying that a moving clock appears to run slow. We often say that time has been dilated or lengthened in the moving observer frame. The time as observed by an observer moving with the clock is less than the one observed by a moving observer.
We highlight the following points
- Time intervals are affected by relative motion.
A stationary clock measures a longer time interval between events occurring in a moving frame of reference than does a clock in the moving frame.
13 Question: Discuss velocity addition theorem?
Solution:
Let S and S’ be two frames of reference such that S’ is moving with respect to S with a uniform speed v in the positive x direction Figure. Consider a particle P which is moving in the frame S. Suppose its position coordinates at time t are (x,y,z).
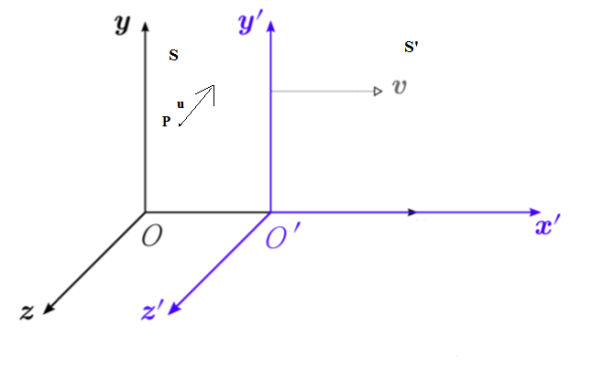
Figure
Then its velocity components in the frame S are
ux =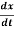 uy =
uy = uz =
uz =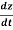 ………….(1)
………….(1)
We wish to find how do these velocity components appear to the observer in the frame S’. If (x’,y’,z’) are the instantaneous position coordinates of the particle P at time t’, then its velocity components in frame S’ are
u’x =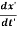 u’y =
u’y =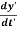 u’z =
u’z = ………….(2)
………….(2)
Consider the Lorentz transformation equations (2) i.e.
x’= 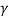 (x-vt)
(x-vt)
y’ =y
z’ = z
t’=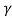 ( t -
( t - 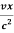 )
)
Where 
Take the differentials of both sides of above equations. This gives
dx’= 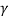 (dx- vdt)………….(3)
(dx- vdt)………….(3)
Dy’ =dy………….(4)
Dz’ = dz………….(5)
Dt’=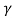 (dt -
(dt - 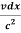 )………….(6)
)………….(6)
Divide equation (3) by (6)
u’x = =
= 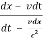
u’x = 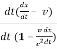
Using equation (1) it becomes
u’x = 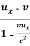
Nowdivide equation (4) by (6)
u’y =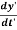 =
= 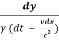
=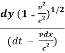
=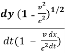
Using equation (1) it becomes
u’y =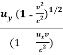
Nowdivide equation (4) by (6)
u’z =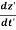 =
=
=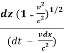
=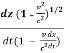
Using equation (1) it becomes
u’z =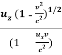
Collecting together equations for u’x ,u’y ,u’z we have
u’x = 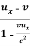 ………….(7)
………….(7)
u’y =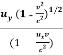 ………….(8)
………….(8)
u’z =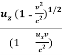 ………….(9)
………….(9)
These equation allow us to observe the observed velocity in frame S and S’ which is in uniform translation motion.
To obtain inverse transformation from S and S’ change dashed quantities to undashed one and vice versa and change v to –v in equation (7), (8) and (9) we get
ux= 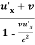 ………….(10)
………….(10)
uy =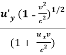 ………….(11)
………….(11)
uz =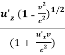 ………….(12)
………….(12)
14 Question:Discuss the variation of mass with velocity?
Solution:
To explain the variation of mass with velocity, consider two frames of references S and S'. S' is moving with constant velocity v along X-direction.
Let us consider two exactly similar balls A and B each of mass m. Both these balls A and B are moving in opposite direction along X-axis with equal speed u' in frame S'.
After collision they merge into one body.
Applying the law of conservation of momentum on the collision of the balls in frame S', we have
Momentum of balls before collision = Momentum of balls after collision
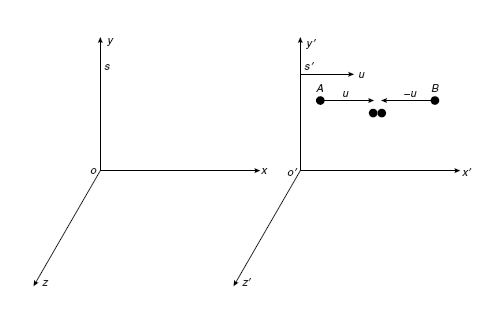
After collision, the merged mass must be at rest in frame S'. Hence, it moves with velocity v in frame S.
Let u1, u2 be the velocities and m1, m2 be the masses of balls A and B, respectively, in frame S.
Using the law of addition of velocities, the above velocities can be written as
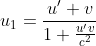 ………(1)
………(1)
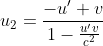 ………(2)
………(2)
Applying the law of conservation of momentum on the collision of the balls in frame s, we have
m1u1 + m2u2 = (m1 + m2)v ………(3)
Substituting u1 and u2 values from Equations (1) and (2), we have
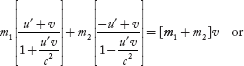
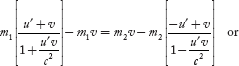
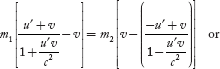
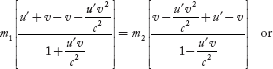

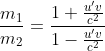 ………(4)
………(4)
The above equation makes a relationship between the masses of balls in frame S and their velocities in frame S'.
Now, to obtain relation between masses of balls and their velocities in frame S, we proceed as follows. Squaring Equation (1)
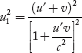
And using the above equation, the value 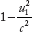 is
is

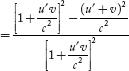
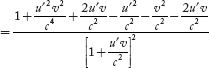
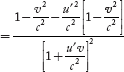
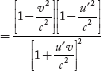
Therefore,
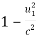 =
= 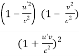 ………(5)
………(5)
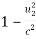 =
= 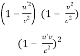 ………(6)
………(6)
Dividing Equation (6) by Equation (5) and taking square root throughout, we have
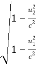 =
= ………(7)
………(7)
Now from equation (4) and (7) we get
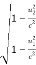 =
=  ……… (8)
……… (8)
Suppose, m2 is at rest in frame S, then u2 = 0 and m2 = m0 (say) where m0 is the rest mass of the ball B, then Equation (8) becomes
 =
= 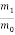 ………(9)
………(9)
As both the balls are similar, hence the rest masses of both balls are the same, so we can write the rest mass of m2 is equal to rest mass of m1, that is equal to mo. Then, Equation (9) becomes
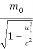 =
= 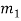 ………(10)
………(10)
Here, m1 is the mass of ball A when it is moving with velocity u1 in frame S. After collision, the merged mass containing mass of ball A moves with velocity v in frame S.
In general, if we take the mass of ball A as m, when it is moving with velocity v in frame S, then
 = m ………(11)
= m ………(11)
Where m0 is the rest mass of the body and m is the effective mass.
Equation (11) is the relativistic formula for the variation of mass with velocity. Here, we see some special cases:
- Case (i)
When the velocity of the body, v is very small compared to velocity of height, c and then  is negligible compared to one. Therefore,
is negligible compared to one. Therefore,
m = m*0
- Case (ii)
If the velocity of the body vis comparable to the velocity of light c, then 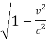 is less than one, so m > mo.
is less than one, so m > mo.
The mass of a moving body appears greater than its rest mass.
- Case (iii)
Suppose the velocity of a body is equal to velocity of light c, then it possess infinite mass.
The effective mass of particles has been experimentally verified by using particle accelerators in case of electrons and protons by increasing their velocities very close to velocity of light.
15 Question: What is Einstein’s mass energy relation?
Solution:
Mass-energy equivalence implies that even though the total mass of a system changes, the total energy and momentum remain constant. Consider the collision of an electron and a proton. It destroys the mass of both particles but generates a large amount of energy in the form of photons.
Mass-energy equivalence states that every object possesses certain energy even in a stationary position.
A stationary body does not have kinetic energy. It only possesses potential energy and probable chemical and thermal energy.
According to the field of applied mechanics, the sum of all these energies is smaller than the product of the mass of the object and square of the speed of light.
Mass-energy equivalence means mass and energy are the same and can be converted into each other.
Einstein put this idea forth but he was not the first to bring this into the light. He described the relationship between mass and energy accurately using his theory of relativity. The equation is known as Einstein's mass-energy equation and is expressed as,
E = mc2
Where E= equivalent kinetic energy of the object.
The mass–energy equivalence gives the relation between the mass and energy.
16 Question: Derive mass energy equation?
Solution:
Derivation of mass energy equation
We know that according to classical mechanics, the rate of change of momentum is proportional to force acting upon the body in the direction of motion.
F = 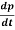 =
= 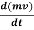 …...... (1)
…...... (1)
According to the theory of relativity, mass and velocity are variable so equation (1) after become.
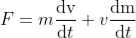 …...... (2)
…...... (2)
The force F acting on the body makes a displacement dx.
We know that work done dw is given by product of force and displacement
And also the work is stored as kinetic energy (dε) in the body. So work done can be written as
Dw = dε = Fdx ...........(3)
Substituting force F from Equation (2) in Equation (3). We get
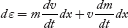
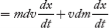
dε = mvdv + v2dm...........(4)
And also velocity v = 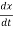
The relativistic mass m is given by
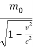 = m
= m
Squaring on both sides, we get
m2 =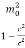 =
= 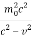
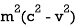 =
=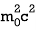 ........... (5)
........... (5)
Differentiating Equation (5), we get
2mc2dm − 2mv2dm − 2m2vdv = 0
c2dm = v2dm + mvdv …........ (6)
Comparing Equations (4) and (6), we get
dε = c2dm ............(7)
By applying force, the mass of a body increases from m0 to m and hence the kinetic energy. The total energy acquired by the body is obtained by integrating Equation (7)
ε = 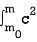 dm =
dm =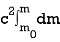 =
=  (m - m0)............ (8)
(m - m0)............ (8)
Therefore increase in kinetic energy is due to the increase in mass of the body. The total energy (E) of the body is the sum of increase in kinetic energy of the body due to motion and the energy at rest (moc2):
∴ E = ε + moc2
Using Equation (8)
E = mc2 − moc2 + moc2 = mc2
E = mc2 …………. (9)
This shows that increase in energy equivalent to increase in mass. In other words anything that increase energy will increase its relativistic mass.
The above equation shows the equivalence between mass and energy also known as Einstein’s mass–energy relation.
17 Question:What do you mean by equipotential surface? Also discuss need of equipotential surface?
Solution:
We already studied about Electric field lines help us to understand electric fields, because they give us a "visual" representation of an Electric field. Each of those lines represents the "direction" of the electric field, because the electric field (vector) is tangent to each point of those lines.
In a similar way, the potential at points inside of an electric field can be represented "graphically" using equipotential surfaces.
An Equipotential surface is a surface where the potential is the same (equal) for any point on top of that surface.
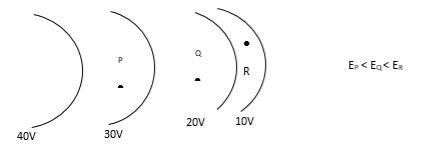
In an area where an electric field exists we can construct an equipotential surface that passes through any point. In the diagrams we only show some equipotential lines, mostly with the same potential difference between neighbouring surfaces. And lasty, no point can have two or more different potentials and so equipotential lines can never be tangent and can never intersect.
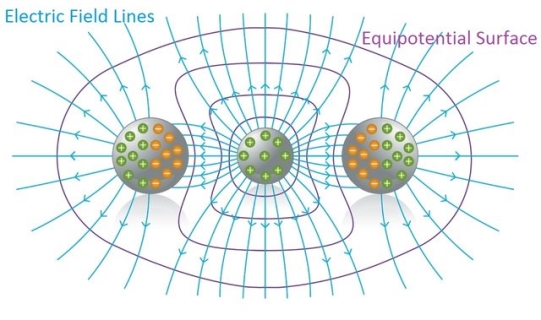
5 Figure
NEED OF EQUIPOTENTIAL SURFACES
When moving "along" an equipotential surface the potential is the same for any point where a test charge passes by. Which means that the electric field E doesn't produce Work to the test charge on top of an equipotential surface. More specifically the electric field E can't have a vector component tangent to that surface, so that this component can produce Work to the motion of the moving charge on top of the surface.
So, the electric field is vertically across to any point of the equipotential surface and to the equipotential surface as a whole. Something which gets us to the conclusion thatElectric field lines and Equipotential surfaces are always vertically across to each other.
Generally, electric field lines are curved lines and equipotential surfaces are curved surfaces. In the special case of a uniform field where the electric field lines are parallel to each other, the equipotential surfaces are parallel surfaces vertically across to the electric field's lines.
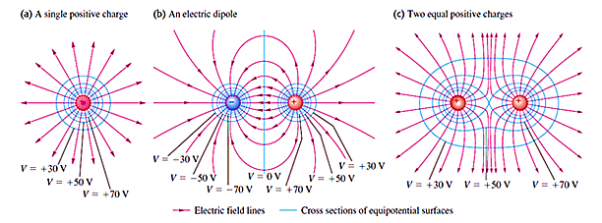
6 Figure: Cross Sections of equipotential surfaces (blue lines) and electric field lines (red lines) for assemblies of point charges. There are equal potentials differences between adjacent surfaces.
When the charges inside of a conductor are not moving (are at "rest") then the electric field directly outside of the conductor must be vertically across to every point on top of it's surface.
Of course the electric field E = 0 in every point inside of the conductor (electrostatics), cause else the charges would be moving. This means that the component of E that is tangent to the surface, inside of the conductor, is zero at every point. Therefore the tangent component of E directly outside of the conductor is also zero. If that was not true then we would violate the laws of electrostatics. And so, the electric field is vertically across to every point of the conductor's surface. As a result, a conductive surface is always an equipotential surface.
When the charges inside of a conductor are not moving (are at "rest") then the electric field directly outside of the conductor must be vertically across to every point on top of it's surface.
Of course the electric field E = 0 in every point inside of the conductor (electrostatics), cause else the charges would be moving. This means that the component of E that is tangent to the surface, inside of the conductor, is zero at every point. Therefore the tangent component of E directly outside of the conductor is also zero. If that was not true then we would violate the laws of electrostatics. And so, the electric field is vertically across to every point of the conductor's surface. As a result an conductive surface is always an equipotential surface.
So we concluded that any surface over which the potential is constant is called an equipotential surface. In other words, the potential difference between any two points on an equipotential surface is zero.No work is required to move a charge from one point to another on the equipotential surface. In other words, any surface with the same electric potential at every point is termed as an equipotential surface.
18 Question:Discuss important properties of equipotential surfaces?
Solution:
- Work done in moving a charge over an equipotential surface is zero.
- The electric field is always perpendicular to an equipotential surface.
- The spacing between equipotential surfaces enables us to identify regions of strong and weak fields.
- Two equipotential surfaces can never intersect. If two equipotential surfaces could intersect, then at the point of intersection there would be two values of electric potential which is not possible.
- For a point charge, the equipotential surfaces are concentric spherical shells.
- For a uniform electric field, the equipotential surfaces are planes normal to the x-axis
- The direction of the equipotential surface is from high potential to low potential.
- Inside a hollow charged spherical conductor the potential is constant. This can be treated as equipotential volume. No work is required to move a charge from the centre to the surface.
- For an isolated point charge, the equipotential surface is a sphere. i.e. Concentric spheres around the point charge are different equipotential surfaces.
- In a uniform electric field, any plane normal to the field direction is an equipotential surface.
- The spacing between equipotential surfaces enables us to identify regions of a strong and weak field i.e. E= −dV/dr ⇒ E ∝ 1/dr
19 Question:What do you meant by gradient? Discuss its physical significance?
Solution:
The gradient is a fancy word for derivative, or the rate of change of a function. It’s a vector (a direction to move) that
- Points in the direction of greatest increase of a function
- Is zero at a local maximum or local minimum (because there is no single direction of increase)
The term "gradient" is typically used for functions with several inputs and a single output (a scalar field). Yes, you can say a line has a gradient (its slope), but using "gradient" for single-variable functions is unnecessarily confusing. Keep it simple.
“Gradient” can refer to gradual changes of colour, but we’ll stick to the math definition. You’ll see the meanings are related.
PHYSICAL SIGNIFICANCE OF GRADIENT
A scalar field may be represented by a series of level surfaces each having a stable value of scalar point function θ. The θ changes by a stable value as we move from one surface to another. These surfaces are known as Gaussian surfaces. Now let the two such surfaces are very close together, be represented by two scalar point functions and (θ + d θ). Let ‘r’ and (r + d θ) be the position vectors of points A and B, on the surfaces θ and (θ + d θ) correspondingly with respect to an origin 0 as shown in Figure. Clearly, the vector AB will be dr. Let the least detachment between the two surfaces ‘dn’ be in the direction of unit usual vector n at A.
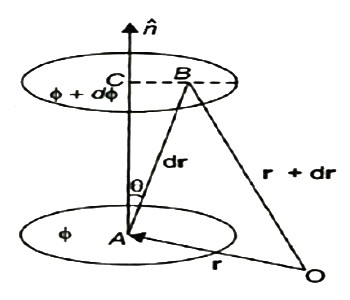
9 Figure
Dn = dr cos θ
= | n | dr | cos θ =n .dr
Dϕ = ∂ϕ/ dn =∂ϕ/dn n .dr…… (1)
Since the continuous scalar function defining the level surfaces (Gaussian surfaces) has a value θ at point A (x, y, z) and (θ + dθ) at point (x + dx, y + dy, z + dz), we have
dϕ = ∂ ϕ/dx dx +dϕ/∂y + ∂ϕ/∂x dz
= (I ∂ϕ/∂x +j ∂ϕ/vy +k ∂ϕ/∂z) .(idx +jdy +kdz)
= ∆ ϕ. Dr … … (2)
From equations (1) and (2), equating the values of d θ,
We obtain ∆θ .dr =∆ϕ= ∂ϕ/ ∂n n .dr
As dr is an arbitrary vector, we have
∆ϕ =∂ϕ/∂ n
Grad ϕ = ∂ ϕ/∂n n
Therefore, the gradient an of a scalar field at any point is a vector field, the scale of which is equal to the highest rate of increase of θ at that point and the direction of it is similar as that of usual to the level surface at that point.
Its physical significance of grad can be understand in terms of the graph of some function z = f(x, y), where f is a reasonable function – say with continuous first partial derivatives. In this case we can think of the graph as a surface whose points have variable heights over the xy – plane. An illustration is given below.
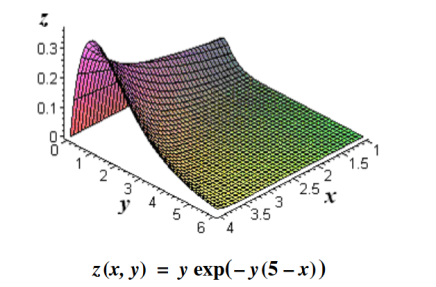
10 Figure
If, say, we place a marble at some point (x, y) on this graph with zero initial force, its motion will trace out a path on the surface, and in fact it will choose the direction of steepest descent. This direction of steepest descent is given by the negative of the gradient of f. One takes the negative direction because the height is decreasing rather than increasing.
Using the language of vector fields, we may restate this as follows: For the given function f(x, y), gravitational force defines a vector field F over the corresponding surface z = f(x, y), and the initial velocity of an object at a point (x, y) is given mathematically by –∇f(x, y). The gradient also describes directions of maximum change in other contexts. For example, if we think off as describing the temperature at a point(x, y), then the gradient gives the direction in which the temperature is increasing most rapidly.
20 Question: Calculate the Distance Travelled by 65.0-kg baseball player slides, given that his initial speed is 6.00 m/s and the force of friction against him is a constant 450 N ?The situation shown in Figure 13. What do you observe from result?
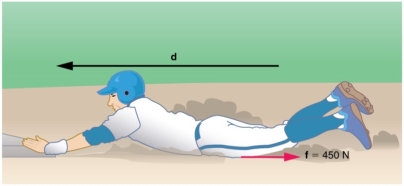
Figure 13
Solution:
The baseball player slides to a stop in a distance d. In the process, friction removes the player’s kinetic energy by doing an amount of work equal to the initial kinetic energy.
Friction stops the player by converting his kinetic energy into other forms, including thermal energy. The work done by friction, which is negative, is added to the initial kinetic energy to reduce it to zero. The work done by friction is negative, because f is in the opposite direction of the motion (that is, θ = 180º, and so cos θ= −1). Thus Wnc = −fd. The equation simplifies to
 mvi2−fd=0
mvi2−fd=0
Or
Fd= 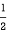 mvi2
mvi2
.
Solving the previous equation for d and substituting known values yields
d= 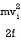 ==
== 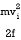
d =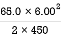 =2.60 m
=2.60 m
The most important point of this example is that the amount of non-conservative work equals the change in mechanical energy. For example, you must work harder to stop a truck, with its large mechanical energy, than to stop a mosquito.
21 Question: Explain Central Forces and Derive equations of motion for a particle in a central force field?
Solution:
Suppose that force acting on a particle of mass m has the properties that:
•the force is always directed from m toward, or away, from a fixed point O,
•the magnitude of the force only depends on the distance r from O
Forces having these properties are called central forces. The particle is said to move in a central force field.
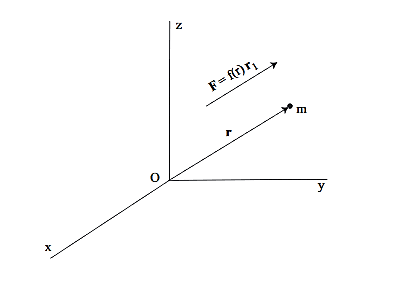
Figure 16:
Mathematically, F is a central force if and only if:
F=f(r)r1= f(r)  ………..(1)
………..(1)
Where r1=  is a unit vector in the direction of r.
is a unit vector in the direction of r.
If f(r) <0 the force is said to be attractive towards O. If f(r)>0 the force is said to be repulsive from O.
For example, the gravitational force of attraction between two point masses is a central force. The Coulomb force of attraction and repulsion between charged particles is a central force.
Properties of a Particle Moving under the Influence of a Central Force
If a particle moves in a central force field then the following properties hold:
1. The path of the particle must be a plane curve, i.e., it must lie in a plane.
2. The angular momentum of the particle is conserved, i.e., it is constant in time.
3. The particle moves in such a way that the position vector (from the point O) sweeps out equal areas in equal times. In other words, the time rate of change in area is constant. This is referred to as the Law of Areas.
Equations of Motion for a Particle in a Central Force Field
Now we will derive the basic equations of motion for a particle moving in a central force field. From Property 1 above, the motion of the particle must occur in a plane, which we take as the xy plane and the center of force is taken as the origin. In Fig. 2 we show the xy plane, as well as the polar coordinate system in the plane.
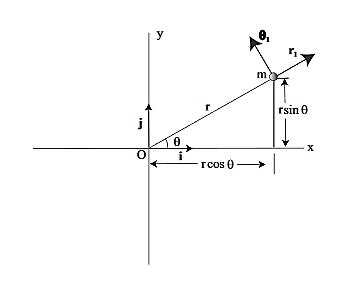
Figure 17: Polar coordinate system associated with a particle moving in the xy plane.
Since the vectorial nature of the central force is expressed in terms of a radial vector from the origin it is most natural (though not required!) to write the equations of motion in polar coordinates. In earlier lectures we derived the expression for the acceleration of a particle in polar coordinates:
 ………..(2)
………..(2)
Then, using Newton’s second law, and the mathematical form for the central force given in (1), we have:
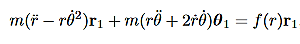 ………..(3)
………..(3)
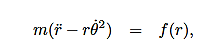 ………..(4)
………..(4)
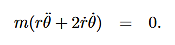 ………..(5)
………..(5)
These are the basic equations of motion for a particle in a central force field. They will be the starting point for many of our investigations. From these equations we can derive a useful constant of the motion. This is done as follows. From (5) we have:
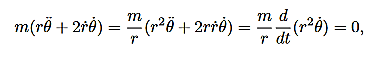
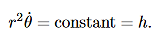 ……….. (6)
……….. (6)
This is an interesting relation that, we will see, is related to properties 2 and 3 above. However, one use for it should be apparent. If you know the r component of the motion it allows you to compute the θcomponent by integration. This is another example of how constants of the motion allow us to “integrate” the equations of motion. It also explains why constants of the motion are often referred to as integrals of the motion. Now, let us return to property 3 above and derive the Law of Areas
Suppose that in time ∆t the position vector moves from r to r+∆r. Then the area swept out by the position vector in this time is approximately half the area of a parallelogram with sides r and ∆r. We give a proof of this:
Area of parallelogram = height×|r|=|∆r|sinθ|r|,
=|r×∆r|,

Figure 18:
Hence,
∆A= |r×∆r|
|r×∆r|
Dividing this expression by ∆t, and letting ∆t→0, gives:
Lim∆t→0

Now we need to evaluate r×v. Using 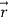 =rr1, we have
=rr1, we have
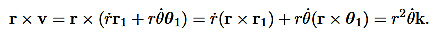
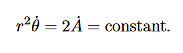 ……….. (7)
……….. (7)

Is called the areal velocity.
Alternative Forms to the Basic Equations of Motion for a Particle in a Central Force Field
Recall the basic equations of motion as they will be our starting point:
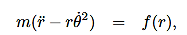 ……….. (8)
……….. (8)
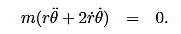 ……….. (9)
……….. (9)
We derived the following constant of the motion:
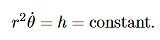 ……….. (10)
……….. (10)
This constant of the motion will allow you to determine the θcomponent of motion, provided you know the r component of motion. However, (8) and (9) are coupled (nonlinear) equations for the r and θcomponents of the motion. How could you solve them without solving for both the r and θcomponents? This is where alternative forms of the equations of motion are useful. Let us rewrite (8) in the following form (by dividing through by the mass m):
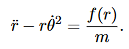 ……….. (11)
……….. (11)
Now, using (10), (11) can be written entirely in terms of r:
 ……….. (12)
……….. (12)
We can use (12) to solve for r(t), and the use (10) to solve for θ(t).Equation (12) is a non-linear differential equation. There is a useful change of variables, which for certain important central forces, turns the equation into a linear differential equation with constant coefficients and these can always be solved analytically. Here we describe this coordinate transformation.
Let r = 
This is part of the coordinate transformation. We will also use θas a new “time” variable. Coordinate transformation are effected by the chain rule, since this allows us to express derivatives of “old” coordinates in terms of the “new” coordinates. We have:
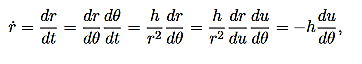 ……….. (13)
……….. (13)
And
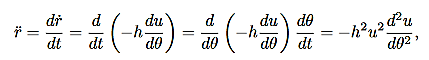 ……….. (14)
……….. (14)
Where, in both expressions, we have used the relation r2 =h at strategic points. Now
=h at strategic points. Now
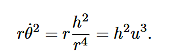 ……….. (15)
……….. (15)
Substituting this relation, along with (14) into (8), gives:
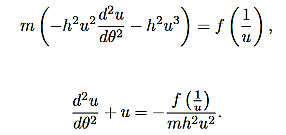 ……….. (16)
……….. (16)
Now if f(r) = 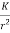 , where K is some constant, (16) becomes a linear, constant coefficient equation
, where K is some constant, (16) becomes a linear, constant coefficient equation
22 Question: How relativistic energy and momentum are related to each other?
Solution:
If m is the relativistic mass of a given particle moving with velocity v then its energy is given by
E = mc2………. (1)
Substitute the value of mass m= 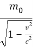 in equation (1)
in equation (1)
E = 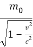 c2………. (2)
c2………. (2)
Squaring both sides we get
E2 = 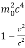 ………. (3)
………. (3)
The magnitude of momentum of a particle is given by
p =mv = 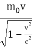
Squaring both sides we get
p2= = 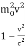 ………. (4)
………. (4)
Multiply both sides by c2 equation (4) become
p2c2 = 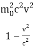 ………. (5)
………. (5)
Subtract equation (5) from equation (3) we get
E2 - p2c2 = 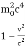 -
- 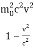
E2 - p2c2 = 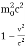 (
(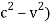
E2 - p2c2 =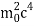
E2 = p2c2 - 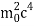
This is energy momentum relation for a free particle.\
23 Question: Discuss examples from nuclear physics?
Solution:
High-energy Physics:
In high-energy collisions, it is common for particles to appear or disappear completely. This seems to violate what we have learnt in school that matter cannot be created or destroyed. The explanation comes from the energy-mass relation, which allows a particle's mass to be entirely converted to other forms of energy and vice versa. Of course, a quick calculation will show that you need large amounts of energy to create even a light particle such as the electron, hence these processes are observed only in high-energy experiments. High-energy physicists therefore find it convenient to express the masses of particles in terms of their equivalent energy. For instance, the mass of an electron is about 0.511 MeV /c2, (about 9.109 x 10-31 kg in conventional terms), and the mass of a proton is about 938 MeV / c2 (about 1.673 x 10-27 kg).
Modern particle accelerators such as the Tevatron in Fermilab near Chicago can co11ide protons and antiprotons with a total energy of 2 million MeV. In fact, the name Tevatron comes from teraelectron volt (TeV), which is equal to a million MeV. With such an energy, one can create a particle which is two thousand times more massive than a proton. In 2007, a more powerful accelerator called the LHC (Large Hadron Collider) will begin working in Geneva; this will collide protons with protons with a total energy of 14 million MeV.
Muon Decay:
There is an unstable particle called the muon which decays into other particles with a time constant of T = 2 microseconds. These particles are created when cosmic rays hit the upper atmosphere, at a distance of tens of kilometres above the Earth's surface. The particles are created at speeds of up to 0.99 c, but even at such high speeds, one would expect that they travel only about 600 meters (in 2 microseconds) be-fore decaying. However, some muons are found near the Earth's surface.
The explanation for this observation comes from the phenomenon of time dilation. The lifetime of 2 microseconds for the muon is true in its rest frame. In the Earth-bound frame, the muon is moving at a speed of 0.99 c, hence its lifetime is given by 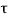 /
/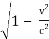 ~ 7
~ 7  ~ 14 microseconds. The average distance that they travel in
~ 14 microseconds. The average distance that they travel in
Fission and Fusion:
In general, the mass of an atom is less than the sum of the masses of the neutrons, protons and electrons contained in it. The mass difference is due to the binding energy; when particles come together to form a bound state, they lose the binding energy EB and therefore a mass given by EB /c2. Most of the binding energy of an atom is due to the nuclear forces which bind neutrons and protons together to form the nucleus; the binding energy of the electrons to the nucleus is about a million times smaller. Roughly speaking, this means that chemical interactions (involving electrons) are a million times weaker than nuclear interactions.
If we look at the binding energy of a nucleus and divide it by the total number of nucleons, we get an average value of the binding energy called the binding energy per nucleon. This is obviously different for different nuclei, but we find that it is largest for an isotope of iron, namely ~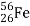 . In this notation,
. In this notation, 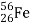 means that the nucleus of the iron atom (Fe) contains 26 protons and 56 -26 =30 neutrons. The binding energy per nucleon for this nucleus is 8.8 million electron volts (MeV), and becomes progressively smaller both for larger and smaller nuclei.
means that the nucleus of the iron atom (Fe) contains 26 protons and 56 -26 =30 neutrons. The binding energy per nucleon for this nucleus is 8.8 million electron volts (MeV), and becomes progressively smaller both for larger and smaller nuclei.
For example, the binding energy per nucleon for the alpha particle (~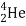 ) is 7.1 MeV. Thus, heavy nuclei are comparatively less stable and can be split into lighter nuclei that are more stable. This process is called fission. Similarly, very light nuclei can be joined together to form more stable heavier nuclei. This process is called fusion. In both processes, the difference in binding energy is released in the form of kinetic energy of the daughter particles. An example of a fission process is the decay of uranium. When a neutron strikes a uranium nucleus, the 'latter can decay into a cesium nucleus and a rubidium nucleus emitting three neutrons and some energy,
) is 7.1 MeV. Thus, heavy nuclei are comparatively less stable and can be split into lighter nuclei that are more stable. This process is called fission. Similarly, very light nuclei can be joined together to form more stable heavier nuclei. This process is called fusion. In both processes, the difference in binding energy is released in the form of kinetic energy of the daughter particles. An example of a fission process is the decay of uranium. When a neutron strikes a uranium nucleus, the 'latter can decay into a cesium nucleus and a rubidium nucleus emitting three neutrons and some energy,
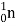 +
+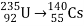 +
+ +3
+3
Since the process starts with one neutron and results in three neutrons being produced, this can have a multiplicative effect in that each of the daughter neutrons can cause further fission of a uranium nucleus, setting off what is called a chain reaction. This is the reaction used in most nuclear power plants today. The fission of 1 kg of uranium releases 18.7 million kilowatt-hours as heat.
An example of a fusion process is the reaction by which two nuclei of a heavy isotope of hydrogen (called the deuteron) join to form a helium nucleus, thereby emitting one neutron and some energy,
 +
+
This is one of the main processes that is responsible for the production of energy in most stars including the sun. Some of this energy eventually reaches the Earth and makes life possible here.
24 Question: Discuss arrival of  meson on the surface of earth as evidence of time dilation?
meson on the surface of earth as evidence of time dilation?
Solution:
 Meson
Meson
There are many unstable fundamental particles in nature such as neutron,  mesons,
mesons, 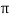 mesons etc. The life time of a
mesons etc. The life time of a 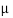 mesons at rest is known from experimental measurements to be equal to 2
mesons at rest is known from experimental measurements to be equal to 2 10-6s. These particles are created by primary cosmic rays at about 10km above the surface of earth and travel with a speed of 0.998c where c is the speed of light. If we assume that the life time of a moving
10-6s. These particles are created by primary cosmic rays at about 10km above the surface of earth and travel with a speed of 0.998c where c is the speed of light. If we assume that the life time of a moving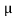 mesons is about 2
mesons is about 2 10-6s, then the distance travelled by the before decaying is
10-6s, then the distance travelled by the before decaying is
l = 0.998c 2
2 10-6
10-6
l = 0.998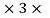 108
108 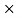 2
2 10-6
10-6 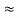 600m
600m
From this argument we can conclude that 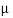 mesons cannot reach the surface of earth as
mesons cannot reach the surface of earth as 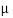 meson must decay during the flight. However experiments have shown that
meson must decay during the flight. However experiments have shown that  mesons do reach the surface of the earth in large numbers. The explanation for this can be obtained from relativistic considerations,
mesons do reach the surface of the earth in large numbers. The explanation for this can be obtained from relativistic considerations,
First explanations, Let us view the situation from the point of view of an observer on the earth, The 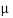 meson is in motion relative to this observer. Thus the life time
meson is in motion relative to this observer. Thus the life time 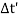 of
of 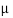 meson while in motion is
meson while in motion is
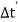 =
= 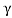 (∆t) =
(∆t) =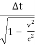
Where ∆t is the life time of 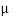 meson at rest , thus
meson at rest , thus
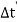 =
= 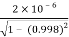 = 31.7
= 31.7  sec
sec
The distance  travelled by
travelled by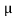 meson in this time is
meson in this time is
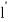 = 31.7
= 31.7 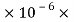 0.998
0.998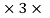 108 = 9500m
108 = 9500m
This is indeed of the order of 10km, thus we concluded that the arrival of  meson on the surface of earth.
meson on the surface of earth.
25 Question: What is Twin Paradox?
Solution:
Twin Paradox
An intriguing consequence of time dilation is that a space traveller moving at a high velocity relative to Earth would age less than the astronaut’s earthbound twin. This is often known as the twin paradox. Imagine the astronaut moving at such a velocity that γ=30.0, as in Figure 33.
A trip that takes 2.00 years in her frame would take 60.0 years in the earthbound twin’s frame. Suppose the astronaut travels 1.00 year to another star system, briefly explores the area, and then travels 1.00 year back. An astronaut who was 40 years old at the start of the trip would be would be 42 when the spaceship returns. Everything on Earth, however, would have aged 60.0 years. The earthbound twin, if still alive, would be 100 years old.
The situation would seem different to the astronaut in Figure 33. Because motion is relative, the spaceship would seem to be stationary and Earth would appear to move. (This is the sensation you have when flying in a jet.) Looking out the window of the spaceship, the astronaut would see time slow down on Earth by a factor of γ=30.0. Seen from the spaceship, the earthbound sibling will have aged only 2/30, or 0.07, of a year, whereas the astronaut would have aged 2.00 years.
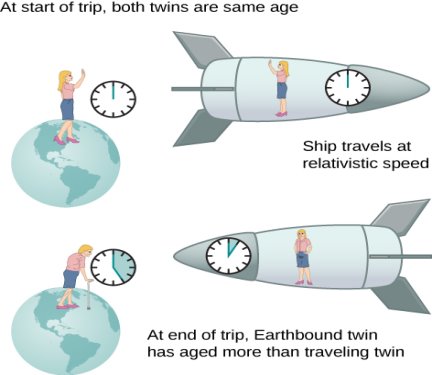
Figure 33: The twin paradox consists of the conflicting conclusions about which twin ages more as a result of a long space journey at relativistic speed.
The paradox here is that the two twins cannot both be correct. As with all paradoxes, conflicting conclusions come from a false premise. In fact, the astronaut’s motion is significantly different from that of the earthbound twin. The astronaut accelerates to a high velocity and then decelerates to view the star system. To return to Earth, she again accelerates and decelerates. The spacecraft is not in a single inertial frame to which the time dilation formula can be directly applied. That is, the astronaut twin changes inertial references. The earthbound twin does not experience these accelerations and remains in the same inertial frame. Thus, the situation is not symmetric, and it is incorrect to claim that the astronaut observes the same effects as her twin. The lack of symmetry between the twins will be still more evident when we analyze the journey later in this chapter in terms of the path the astronaut follows through four-dimensional space-time.
In 1971, American physicists Joseph Hafele and Richard Keating verified time dilation at low relative velocities by flying extremely accurate atomic clocks around the world on commercial aircraft. They measured elapsed time to an accuracy of a few nanoseconds and compared it with the time measured by clocks left behind. Hafele and Keating’s results were within experimental uncertainties of the predictions of relativity. Both special and general relativity had to be taken into account, because gravity and accelerations were involved as well as relative motion.
26 Question: What is meant by divergence, curl and their physical significance?
Solution:
Divergence and curl are two measurements of vector fields that are very useful in a variety of applications. Both are most easily understood by thinking of the vector field as representing a flow of a liquid or gas; that is, each vector in the vector field should be interpreted as a velocity vector.
Divergence measures the tendency of the fluid to collect or disperse at a point, and curl measures the tendency of the fluid to swirl around the point. Divergence is a scalar, that is, a single number, while curl is itself a vector. The magnitude of the curl measures how much the fluid is swirling, the direction indicates the axis around which it tends to swirl.
DIVERGENCE
Consider water flowing through a large pipe. Now, it has smaller pipes joined to it. Hence, as the water flows, more water is added along the way by the smaller pipes. Hence, the mass flow rate increases as the water flows.
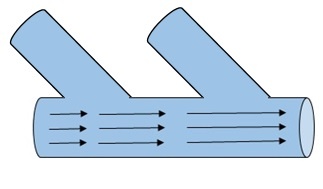
11 Figure
In another case, consider that there is a leakage in the pipe. Hence the mass flow rate decreases as it flows. This change in the flow rate through the pipe, whether it increases or decreases, is called as divergence. Divergence denotes only the magnitude of change and so, it is a scalar quantity. It does not have a direction.
When the initial flow rate is less than the final flow rate, divergence is positive (divergence > 0). If the two quantities are same, divergence is zero. If the initial flow rate is greater than the final flow rate divergence is negative (divergence <0).
Recall that if f is a function, the gradient of f is given by
∇f=⟨∂f/∂x, ∂f/∂y, ∂f/∂z⟩
Where
∇=⟨∂/∂x, ∂/∂y, ∂/∂z⟩
The divergence can be defined in terms of this same odd vector ∇ by using the dot product. The divergence of a vector field F=⟨f,g,h⟩ is


12 Figure
Physical Interpretation of the Divergence
For an electric field:∇·E= ρ/ε, that is there are sources of electric field. Consider a vector field F that represents a fluid velocity: The divergence of F at a point in a fluid is a measure of the rate at which the fluid is flowing away from or towards that point.
A positive divergence is indicating a flow away from the point. ƒ Physically divergence means that either the fluid is expanding or that fluid is being supplied by a source external to the field. ƒ The lines of flow diverge from a source and converge to a sink.
If there is no gain or loss of fluid anywhere then div F= 0. Such a vector field is said to be solenoidal.
Air leaving a punctured tire: Divergence is positive, as closed surface (tire) exhibits net outflow.
CURL
Imagine pouring water in a cup. The water won’t just low linearly but rather, as it reaches the end of the cup, it will flow in a rotational motion before settling in the cup. Or consider water draining down the sink, it will swirl in a rotational motion before going out. If we plot this rotational flow of water as vectors and measure it, it will denote the Curl.

13 Figure
Curl is a measure of how much a vector field circulates or rotates about a given point. when the flow is counter-clockwise, curl is considered to be positive and when it is clock-wise, curl is negative. Sometimes, curl isn’t necessarily flow around a single time. It can also be any rotational or curled vector.
For example, curl can help us predict the voracity, which is one of the causes of increased drag. By using curl, we can calculate how intense it is and reduce it effectively. Calculating divergence helps us understand the flow rate and correct it to suit our needs.
The curl can be defined in terms of this same odd vector ∇ by using the cross product. The curl of a vector field F=⟨f,g,h⟩ is
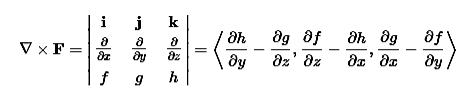
Physical Interpretation of the Curl
Consider a vector field F that represents a fluid velocity:
The curl of F at a point in a fluid is a measure of the rotation of the fluid.
If there is no rotation of fluid anywhere then ∇x F= 0. Such a vector field is said to be irrotational or conservative.
An electrostatic field (denoted by E) has the property ∇x E= 0, an irrotational (conservative) field.