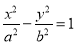Question Bank
Unit 3
1. List out different conics section?
Ans –
Conic sections:
The section obtained by intersection of a right circular cone by a plane in different positions relative to the axis of the cone are called conics.
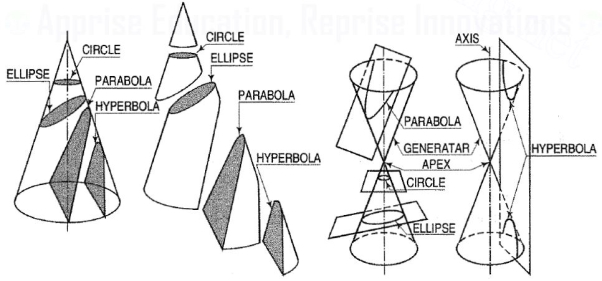
Figure 1
(i) When the section plane is inclined to the axis and cuts all the generators onone side of the apex, the section is an ellipse [fig. 1].
(ii) When the section plane is inclined to the axis and is parallel to one of the generators, the section is a parabola [fig. 1].
(iii) A hyperbola is a plane curve having two separate parts or branches, formedwhen two cones that point towards one another are intersected by a planethat is parallel to the axes of the cones.
Conic sections are always "smooth". More precisely, they never contain any inflection points. This is important for many applications, such as aerodynamics, civil engineering, mechanical engineering, etc.
2. List out conics based on eccentricity.
Ans –
The conic may be defined as the locus of a point in a plane, wherein the ratio of its distance from a fixed point and a fixed straight line is always constant. The fixed point is called the focus and the fixed line, the directrix.
The ratio 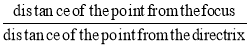 is called eccentricity and is denoted by ‘e’. It is always less the 1 for ellipse, equal to 1 for parabola and greater than 1 for hyperbola i.e.
is called eccentricity and is denoted by ‘e’. It is always less the 1 for ellipse, equal to 1 for parabola and greater than 1 for hyperbola i.e.
(i) ellipse: e < 1
(ii) parabola: e = 1
(iii) hyperbola: e > 1
3. List out steps for construction of ellipse by arcs of circles method.
Ans –
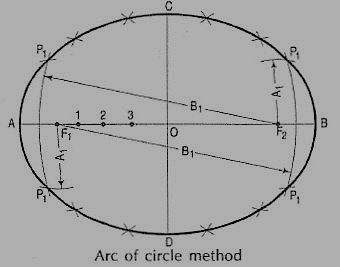
(i) Draw a line AB equal to themajor axis and a line CO equalto the minor axis, bisecting eachother at right angles at O.
(ii) With centre C and radius equal to half AB (i.e. AO) draw arcscutting AB at F1 and F2, thefoci of the ellipse.
(iii) Mark many points 1, 2,3 etc. on AB.
(iv) With centres F1 and F2 andradius equal to A1, draw arcson both sides of AB.
(v) With same centres and radius equal to 81, draw arcs intersecting theprevious arcs at four points marked P1.
(vi) Similarly, with radii A2 and B2, A3 and B3 etc. obtain more points.
(vii) Draw a smooth curve through these points. This curve is the required ellipse.
4. List out steps for drawing ellipse based on concentric circles method.
Ans –
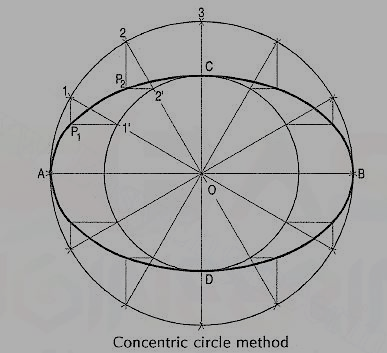
(i) Draw the major axis AB and the minor axis CD intersecting each other at O.
(ii) With centre O and diameters AB and CD respectively, draw two circles.
(iii) Divide the major-axis-circle into many equal divisions, say 12 andmark points 1, 2 etc. as shown.
(iv) Draw lines joining these points with the centre O and cutting the minor-axis-circleat points 1', 2' etc.
(v) Through point 1 on the major-axis-circle, draw a line parallel to CD, the minor axis.
(vi) Through point 1' on the minor-axis-circle, draw a line parallel to AB, the majoraxis. The point P1, where these two lines intersect is on the required ellipse.
(vii) Repeat the construction through all the points. Draw the ellipse through A,P1, P2 …etc.
5. List out steps for drawing ellipse based on Oblong method.
Ans –
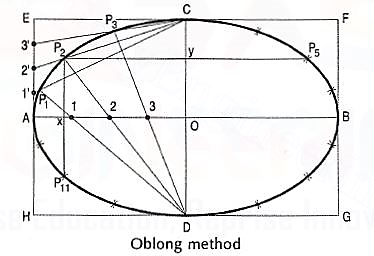
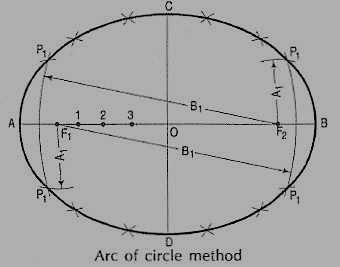
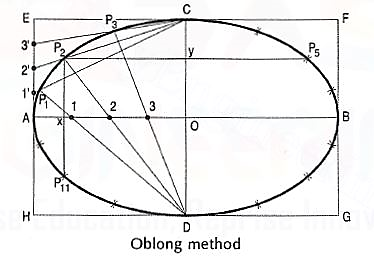
(i) Draw the two axes AB and CD intersecting each other at O.
(ii) Construct the oblong EFGH having its sides equal to the two axes.
(iii) Divide the semi-major-axis AO into many equal parts, say 4, and AE into the same number of equal parts, numbering them from A as shown.
(iv) Draw lines joining 1 ', 2' and 3' with C.
(v) From D, draw lines through 1, 2 and 3 intersecting C'1, C'2 and C'3 at points P1, P2 and P3 respectively.
(vi) Draw the curve through A, P1..... C. It will be one quarter of the ellipse.
(vii) Complete the curve by the same construction in each of the three remaining quadrants.
As the curve is symmetrical about the two axes, points in the remaining quadrantsmay be located by drawing perpendiculars and horizontals from P1, P2 etc. andmaking each of them of equal length on both the sides of the two axes.
6. Explain Tangent method to draw Parabola.
Ans –
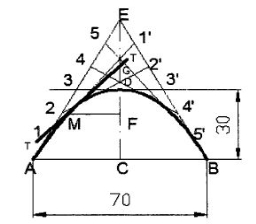
1. Draw the base AB and locate its mid-point C.
2. Through C, draw CD perpendicular to AB forning the axis
3. Produce CD to E such that DE = CD
4. Join E-A and E-B. These are the tangents to the parabola at A and B.
5. Divide AE and BE into the same number of equal parts and number the points as shown.
6. Join 1-1' ,2- 2' ,3- 3' , etc., forming the tangents to the required parabola.
7. A smooth curve passing through A, D and B and tangential to the above lines is therequired parabola.
7. Explain directrix and focus method for construction of parabola.
Ans –
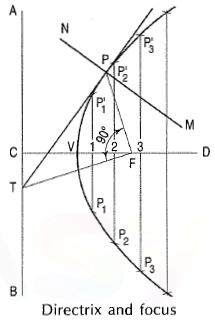
To construct a parabola, when the distance of the Focusfrom the directrix is 50 mm.
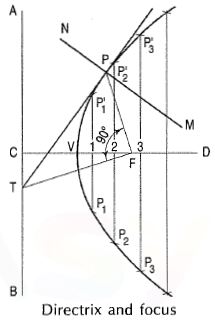 (i) Draw the directrix AB and the axis CD.
(i) Draw the directrix AB and the axis CD.
(ii) Mark focus Fon CD, 50 mm from C.
(iii) Bisect CF in V the vertex (because eccentricity = 1).
(iv) Mark many points 1, 2, 3 etc. on the axisand through them, draw perpendiculars to it.
(v) With centre F and radius equal to C1, draw arcs cutting the perpendicular through 1 at P1 and P’1.
(vi) Similarly, locate points P2 and P’2, P3 and P’3 etc. on both the sides of the axes.
(vii) Draw a smooth curve through these points. This curve is the required parabola. It is an open curve.
8. Rectangular Hyperbola.
Ans –
It is a curve traced out by a point moving in such away that the product of its distances from two fixed lines at right angles to eachother is a constant. The fixed lines are called asymptotes.
This curve graphically represents the Boyle's Law, viz. P x V = a, P = pressure,V = volume and a is constant. It is also useful in design of water channels.
General method of construction of a hyperbola:
Mathematically, we can describe a hyperbola by
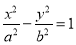
Question Bank
Unit 3
Question Bank
Unit 3
1. List out different conics section?
Ans –
Conic sections:
The section obtained by intersection of a right circular cone by a plane in different positions relative to the axis of the cone are called conics.

Figure 1
(i) When the section plane is inclined to the axis and cuts all the generators onone side of the apex, the section is an ellipse [fig. 1].
(ii) When the section plane is inclined to the axis and is parallel to one of the generators, the section is a parabola [fig. 1].
(iii) A hyperbola is a plane curve having two separate parts or branches, formedwhen two cones that point towards one another are intersected by a planethat is parallel to the axes of the cones.
Conic sections are always "smooth". More precisely, they never contain any inflection points. This is important for many applications, such as aerodynamics, civil engineering, mechanical engineering, etc.
2. List out conics based on eccentricity.
Ans –
The conic may be defined as the locus of a point in a plane, wherein the ratio of its distance from a fixed point and a fixed straight line is always constant. The fixed point is called the focus and the fixed line, the directrix.
The ratio  is called eccentricity and is denoted by ‘e’. It is always less the 1 for ellipse, equal to 1 for parabola and greater than 1 for hyperbola i.e.
is called eccentricity and is denoted by ‘e’. It is always less the 1 for ellipse, equal to 1 for parabola and greater than 1 for hyperbola i.e.
(i) ellipse: e < 1
(ii) parabola: e = 1
(iii) hyperbola: e > 1
3. List out steps for construction of ellipse by arcs of circles method.
Ans –
(i) Draw a line AB equal to themajor axis and a line CO equalto the minor axis, bisecting eachother at right angles at O.
(ii) With centre C and radius equal to half AB (i.e. AO) draw arcscutting AB at F1 and F2, thefoci of the ellipse.
(iii) Mark many points 1, 2,3 etc. on AB.
(iv) With centres F1 and F2 andradius equal to A1, draw arcson both sides of AB.
(v) With same centres and radius equal to 81, draw arcs intersecting theprevious arcs at four points marked P1.
(vi) Similarly, with radii A2 and B2, A3 and B3 etc. obtain more points.
(vii) Draw a smooth curve through these points. This curve is the required ellipse.
4. List out steps for drawing ellipse based on concentric circles method.
Ans –

(i) Draw the major axis AB and the minor axis CD intersecting each other at O.
(ii) With centre O and diameters AB and CD respectively, draw two circles.
(iii) Divide the major-axis-circle into many equal divisions, say 12 andmark points 1, 2 etc. as shown.
(iv) Draw lines joining these points with the centre O and cutting the minor-axis-circleat points 1', 2' etc.
(v) Through point 1 on the major-axis-circle, draw a line parallel to CD, the minor axis.
(vi) Through point 1' on the minor-axis-circle, draw a line parallel to AB, the majoraxis. The point P1, where these two lines intersect is on the required ellipse.
(vii) Repeat the construction through all the points. Draw the ellipse through A,P1, P2 …etc.
5. List out steps for drawing ellipse based on Oblong method.
Ans –
(i) Draw the two axes AB and CD intersecting each other at O.
(ii) Construct the oblong EFGH having its sides equal to the two axes.
(iii) Divide the semi-major-axis AO into many equal parts, say 4, and AE into the same number of equal parts, numbering them from A as shown.
(iv) Draw lines joining 1 ', 2' and 3' with C.
(v) From D, draw lines through 1, 2 and 3 intersecting C'1, C'2 and C'3 at points P1, P2 and P3 respectively.
(vi) Draw the curve through A, P1..... C. It will be one quarter of the ellipse.
(vii) Complete the curve by the same construction in each of the three remaining quadrants.
As the curve is symmetrical about the two axes, points in the remaining quadrantsmay be located by drawing perpendiculars and horizontals from P1, P2 etc. andmaking each of them of equal length on both the sides of the two axes.
6. Explain Tangent method to draw Parabola.
Ans –

1. Draw the base AB and locate its mid-point C.
2. Through C, draw CD perpendicular to AB forning the axis
3. Produce CD to E such that DE = CD
4. Join E-A and E-B. These are the tangents to the parabola at A and B.
5. Divide AE and BE into the same number of equal parts and number the points as shown.
6. Join 1-1' ,2- 2' ,3- 3' , etc., forming the tangents to the required parabola.
7. A smooth curve passing through A, D and B and tangential to the above lines is therequired parabola.
7. Explain directrix and focus method for construction of parabola.
Ans –
To construct a parabola, when the distance of the Focusfrom the directrix is 50 mm.
 (i) Draw the directrix AB and the axis CD.
(i) Draw the directrix AB and the axis CD.
(ii) Mark focus Fon CD, 50 mm from C.
(iii) Bisect CF in V the vertex (because eccentricity = 1).
(iv) Mark many points 1, 2, 3 etc. on the axisand through them, draw perpendiculars to it.
(v) With centre F and radius equal to C1, draw arcs cutting the perpendicular through 1 at P1 and P’1.
(vi) Similarly, locate points P2 and P’2, P3 and P’3 etc. on both the sides of the axes.
(vii) Draw a smooth curve through these points. This curve is the required parabola. It is an open curve.
8. Rectangular Hyperbola.
Ans –
It is a curve traced out by a point moving in such away that the product of its distances from two fixed lines at right angles to eachother is a constant. The fixed lines are called asymptotes.
This curve graphically represents the Boyle's Law, viz. P x V = a, P = pressure,V = volume and a is constant. It is also useful in design of water channels.
General method of construction of a hyperbola:
Mathematically, we can describe a hyperbola by