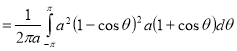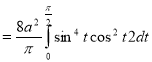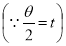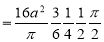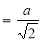Unit - 5
Multiple Integrals
- Evaluate

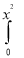 ey/x dy dx.
ey/x dy dx.
Soln. :
Given : I = 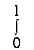
 ey/x dy dx
ey/x dy dx
Here limits of inner integral are functions of y therefore integrate w.r.t y,
I = 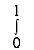
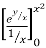
 dx
dx
= 
= 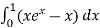
I = 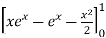
= 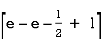 =
= 
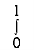
 ey/x dy dx =
ey/x dy dx = 
2. Evaluate 
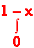 x
x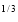 y
y (1 – x –y)
(1 – x –y)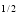 dx dy.
dx dy.
Soln. :
Given : I = 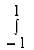
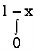 x
x y
y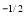 (1 – x –y)
(1 – x –y) dx dy.
dx dy.
Here the limits of inner integration are functions of y therefore first integrate w.r.t y.
I =  x
x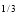 dx
dx 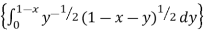
Put 1 – x = a (constant for inner integral)
I = 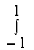 x
x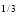 dx
dx 
Put y = at dy = a dt
y | 0 | a |
t | 0 | 1 |
I =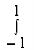 x
x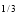 dx
dx 
I = 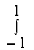 x
x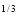 dx
dx 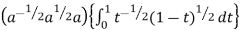
I =  x
x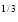 a dx
a dx 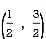
I = 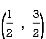
 x
x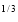 (1 – x) dx =
(1 – x) dx = 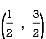
 (x
(x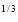 – x4/3) dx
– x4/3) dx
I = 

= 
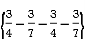
I = 
 =
= 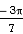
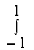
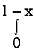 x
x y
y (1 – x –y)
(1 – x –y)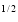 dx dy =
dx dy = 
3. Evaluate 


Soln. :
Let, I = 


Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.
I = 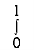 dy
dy 
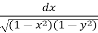
I = 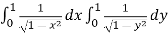
= 
= 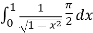
= 
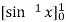
= 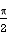
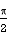
= 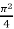
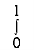
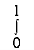
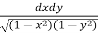 =
= 
4. Evaluate 
 e–x2 (1 + y2) x dx dy.
e–x2 (1 + y2) x dx dy.
Soln. :
Let I = 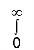
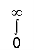 e–x2 (1 + y2) x dy =
e–x2 (1 + y2) x dy =  dy
dy 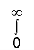 e–x2 (1 + y2) x dy
e–x2 (1 + y2) x dy
= 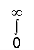 dy
dy  e– x2 (1 + y2)
e– x2 (1 + y2)  dx
dx
= 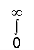
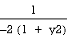 dy
dy  [∵ f (x) ef(x) dx = ef(x) ]
[∵ f (x) ef(x) dx = ef(x) ]
= 
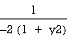 (–1) dy (∵ e– = 0)
(–1) dy (∵ e– = 0)
= 
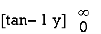 =
= 
 =
= 
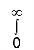
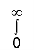 e–x2 (1 + y2) xdx dy =
e–x2 (1 + y2) xdx dy = 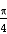
5. Evaluate y dx dy over the area bounded by x= 0 y =  and x + y = 2 in the first quadrant
and x + y = 2 in the first quadrant
Soln. :
The area bounded by y = x2 (parabola) and x + y = 2 is as shown in Fig.6.2
The point of intersection of y = x2 and x + y = 2.
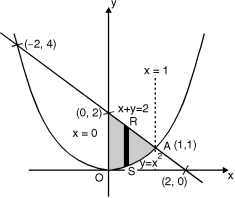
x + x2 = 2 x2 + x – 2 = 0
x = 1, – 2
At x = 1, y = 1 and at x = –2, y = 4
Fig. 6.2
(1, 1) is the point of intersection in Ist quadrant. Take a vertical strip SR, Along SR x constant and y varies from S to R i.e. y = x2 to y = 2 – x.
Now slide strip SR, keeping IIel to y-axis, therefore y constant and x varies from x = 0 to x = 1.
I = 
= 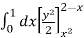
= 
= 
 (4 – 4x +
(4 – 4x +  –
– 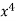 ) dx
) dx
= 
 =
= 
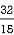
I = 16/15
6. Evaluate  over x 1, y
over x 1, y 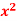
Soln. :
 Let I =
Let I = 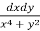 over x 1, y
over x 1, y 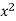
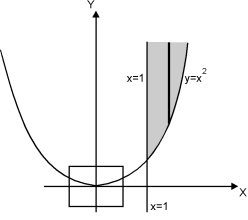
The region bounded by x 1 and y 
Is as shown in Fig. 6.3.
Fig. 6.3
Take a vertical strip along strip x constant and y varies from y = 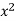
To y = . Now slide strip throughout region keeping parallel to y-axis. Therefore y constant and x varies from x = 1 to x = .
I = 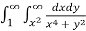
= 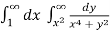
= 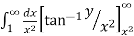 [ ∵
[ ∵ dx =
dx =  tan–1 (x/a)]
tan–1 (x/a)]
= 
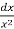
 =
= 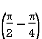
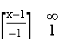
= – 
 =
= 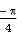 (0 – 1)
(0 – 1)
I = 
7. Change the order of integration for the integral 
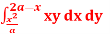 and evaluate the same with reversed order of integration.
and evaluate the same with reversed order of integration.
Soln. :
Given, I = 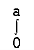
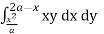 …(1)
…(1)
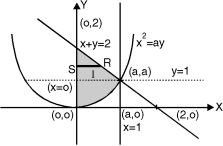 In the given integration, limits are
In the given integration, limits are
y =  , y = 2a – x and x = 0, x = a
, y = 2a – x and x = 0, x = a
The region bounded by x2 = ay, x + y = 2a Fig.6.5
And x = 0, x = a is as shown in Fig. 6.5
Here we have to change order of Integration. Given the strip is vertical.
Now take horizontal strip SR.
To take total region, Divide region into two parts by taking line y = a.
1 st Region :
Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIel to x-axis therefore y varies from y = a to y = 2a.
I1 = 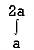 dy
dy  xy dx …(2)
xy dx …(2)
2nd Region :
Along strip, y constant and x varies from x = 0 to x = 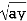 . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
. Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
I2 = 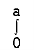 dy
dy 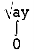 xy dx …(3)
xy dx …(3)
From Equation (1), (2) and (3),
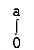
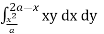 =
=  dy
dy 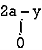 xy dx +
xy dx + 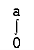 dy
dy 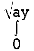 xy dx
xy dx
= 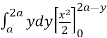 +
+ 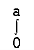 y dy
y dy 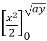
=
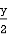
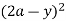 dy +
dy + 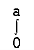
 (ay) dy =
(ay) dy = 
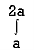 y (4a2 – 4ay + y2) dy +
y (4a2 – 4ay + y2) dy + 
 ay2 dy
ay2 dy
= 
 (4a2 y – 4ay2 + y3) dy +
(4a2 y – 4ay2 + y3) dy + 
 y2 dy
y2 dy
= 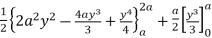
= 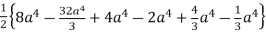 +
+ 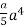
=  a4
a4
8. Evaluate
Soln. :
The region of integration bounded by
y = 0, y = 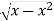 and x = 0, x = 1
and x = 0, x = 1
y = 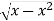 x2 + y2 = x
x2 + y2 = x
The region bounded by these is as shown in Fig. 6.8.
Convert the integration in polar co-ordinates by using x = r cos , y = r sin and dx dy = r dr d
x2 + y2 = x becomes r = cos
y = 0 becomes r sin = 0 = 0
x = 0 becomes r cos = 0 = 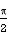
And x = 1 becomes r = sec Fig. 6.8
Take a radial strip SR with angular thickness , Along strip constant and r varies from r = 0 to r = cos . Turning strip throughout region therefore varies from = 0 to = 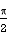
I = 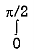

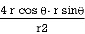
 r dr d
r dr d
=  4 cos sin d r
4 cos sin d r 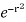 dr
dr
= 4  cos sin d
cos sin d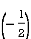 [–
[–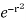 ]
]
= – 2 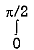 cos sin [
cos sin [ +1] d
+1] d
= – 2 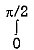 [cos sin
[cos sin 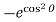 – cos sin ] d
– cos sin ] d
= –2  + 2
+ 2 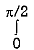 cos sin d
cos sin d
= –  + 2
+ 2 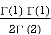
= 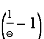 + 1 =
+ 1 = 
9. Evaluate r4 cos3 dr d over the interior of the circle r = 2a cos
Soln. :
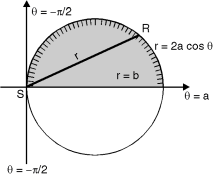 The region of the integration is as shown in Fig. 6.10.Take a radial strip SR, along strip constant and r varies from r = 0 to r = 2a cos. Now turning this strip throughout region therefore varies from =
The region of the integration is as shown in Fig. 6.10.Take a radial strip SR, along strip constant and r varies from r = 0 to r = 2a cos. Now turning this strip throughout region therefore varies from =  to =
to = 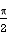
I = 
 r4 cos3 dr d
r4 cos3 dr d
= 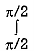 cos3 d
cos3 d
= 
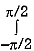 cos3 cos5 d
cos3 cos5 d
= 
 cos8 d Fig. 6.10
cos8 d Fig. 6.10
= 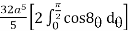
=  2
2 

I = 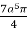
r4 cos3 dr d = 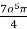
10. Find the area between the curves 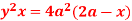 and its asymptote.
and its asymptote.
Solution: The curve is symmetrical about x axis not passing through origin. Also 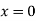 is the asymptote to the curve and intersect x axis at
is the asymptote to the curve and intersect x axis at 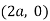 for
for 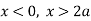 curve doesn’t exists. And for
curve doesn’t exists. And for 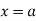 and
and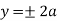 . Because of symmetry
. Because of symmetry
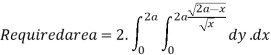
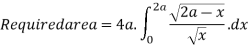
Put 
x | 0 | 2a |
t | 0 | 1 |
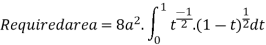

11. Evaluate

Solution : Let
I = 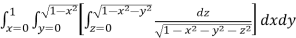
= 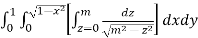
(Assuming m = 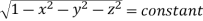 )
)
= 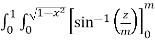 dxdy
dxdy
= 
=
= 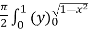 dx
dx
=  dx
dx
= 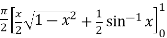
=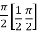
I =
12. Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane
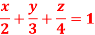
Solution: Volume =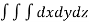 ………. (1)
………. (1)
Put  ,
, 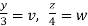
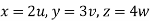
From equation (1) we have
V = 
=24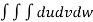
=24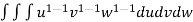 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 
=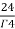 =
= = 4
= 4
Volume =4
13. 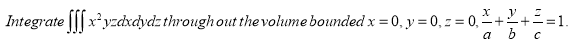

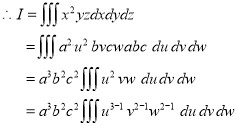
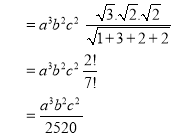
14. Find mean value and R.M.S. Value of the ordinate of cycloid
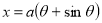 ,
, 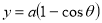 over the range
over the range 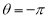 to
to 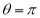 .
.
Sol Let P(x,y) be any point on the cycloid . Its ordinate is y.

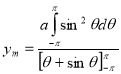
= 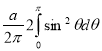
=
=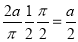
R.M.S.Value=