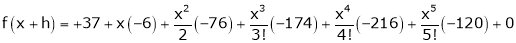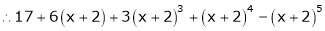Unit - 3
Applications of Partial differentiation
- Find Maclaurin’s Expansion’s for log sec x.
Solution:
Let f(x) = log sec x
 By Maclaurin’s Expansion’s,
By Maclaurin’s Expansion’s,
 (1)
(1)

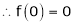
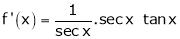
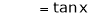

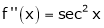
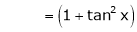

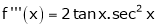
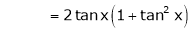

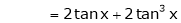
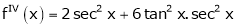
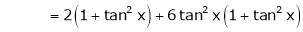
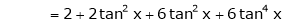

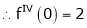
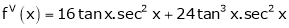
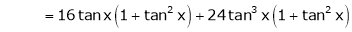
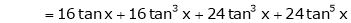

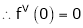
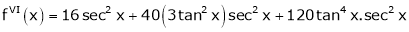
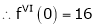
 By equation (1)
By equation (1)
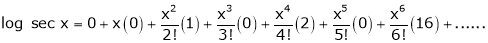
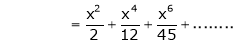
2. Prove that 
Solution:
Here f(x) = x cosec x
= 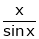
Now we know that
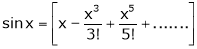


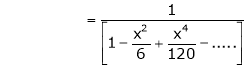
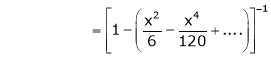
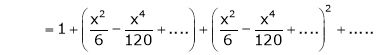
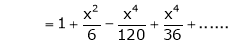

3. Expand  upto x6
upto x6
Solution:
Here 
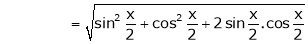
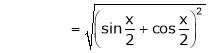
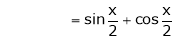
Now we know that
 … (1)
… (1)
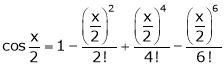 … (2)
… (2)
Adding (1) and (2) we get
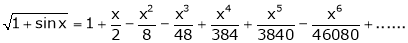
4. Show that 
Solution:
Here 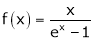
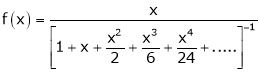
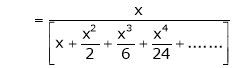
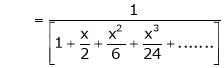
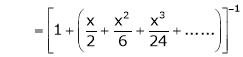

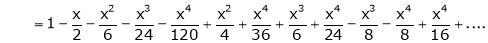
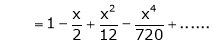
Thus

5. Expand 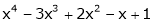 in power of (x – 3)
in power of (x – 3)
Solution:
Let 
Here a = 3
Now by Taylor’s series expansion,
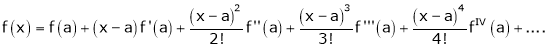 … (1)
… (1)
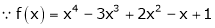
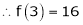
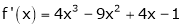
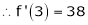
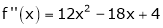
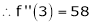
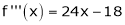
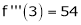

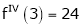
 equation (1) becomes.
equation (1) becomes.

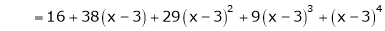
6. Using Taylors series method expand
 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here 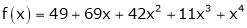
a = -2
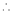 By Taylors series,
By Taylors series,
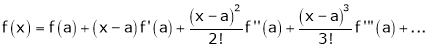 … (1)
… (1)
Since
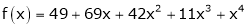
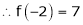

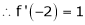
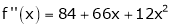
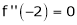
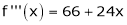
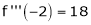
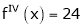
 ,
, 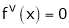 , …..
, …..
Thus equation (1) becomes
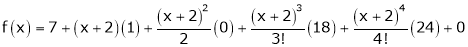
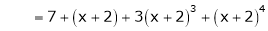
7. Expand  in ascending powers of x.
in ascending powers of x.
Solution:
Here

i.e. 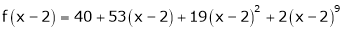
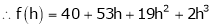
Here h = -2
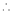 By Taylors series,
By Taylors series,
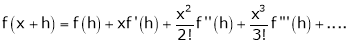 … (1)
… (1)
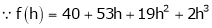
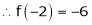
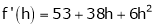

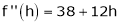
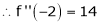
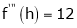
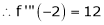
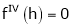
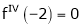
 equation (1) becomes,
equation (1) becomes,
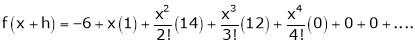
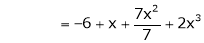
Thus

8. Decampere a positive number ‘a’ in to three parts, so their product is maximum
Solution:
Let x, y, z be the three parts of ‘a’ then we get.
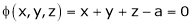 … (1)
… (1)
Here we have to maximize the product
i.e. 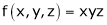
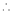 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,
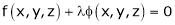
 … (2)
… (2)
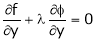 … (3)
… (3)
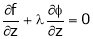 … (4)
… (4)
i.e.
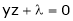 … (2)’
… (2)’
 … (3)’
… (3)’
 … (4)
… (4)
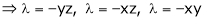
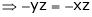
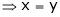
And 
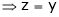
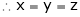
From (1)
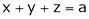

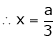
Thus  .
.
Hence their maximum product is 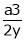 .
.
9. Find the point on plane 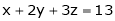 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let 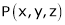 be the point on sphere
be the point on sphere  which is nearest to the point
which is nearest to the point  . Then shortest distance.
. Then shortest distance.
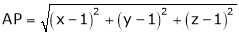
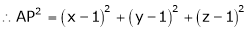
 Let
Let 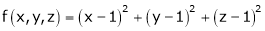
Under the condition  … (1)
… (1)
 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
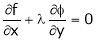
 … (2)
… (2)
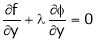
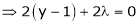 … (3)
… (3)
i.e. 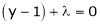 &
&
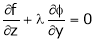
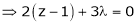 … (4)
… (4)
From (2) we get 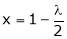
From (3) we get 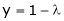
From (4) we get 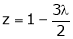
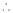 Equation (1) becomes
Equation (1) becomes

i.e. 
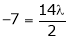
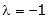

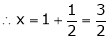
y = 2

If 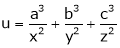 where x + y + z = 1.
where x + y + z = 1.
Prove that the stationary value of u is given by,
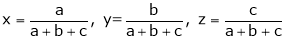
10. Expand 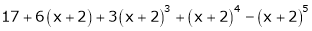 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
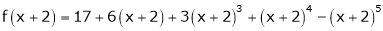
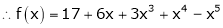
i.e. 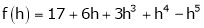
Here
h = 2
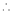 By Taylors series
By Taylors series
 … (1)
… (1)

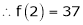
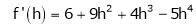


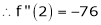

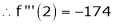
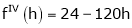
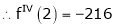



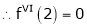
 By equation (1)
By equation (1)