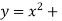Unit-2
Multivariable Calculus-II
Q1: Evaluate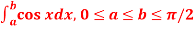 .
.
A1. Here we notice that f:x→cos x is a decreasing function on [a , b],
Therefore by the definition of the definite integrals-
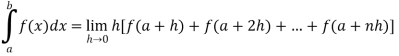
Then
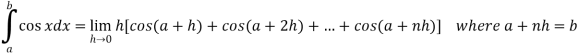
Now,
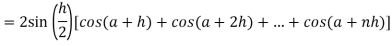
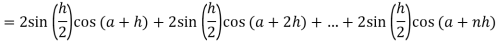
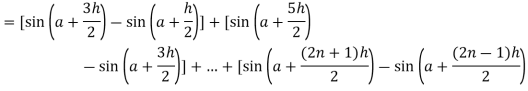
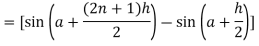
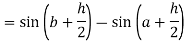
Here 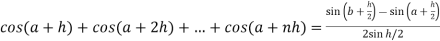
Thus
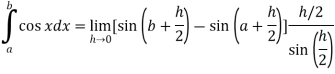
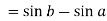
Q2: Evaluate 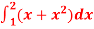
A2. Here 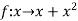 is an increasing function on [1 , 2]
is an increasing function on [1 , 2]
So that,
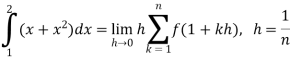
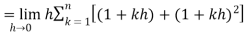
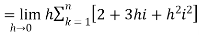
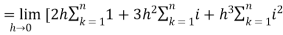 …. (1)
…. (1)
We know that-
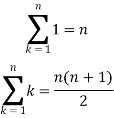
And 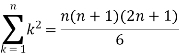
Then equation (1) becomes-
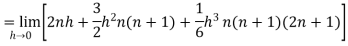
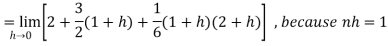

Q3: Find out the integral 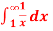 is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
A3. Here we will convert the integral into limit ,
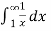 =
= 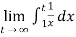
= 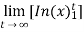
= 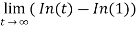
= ∞
As we can see, here limit does not exist. i.e. that is infinity.
So we can say that the given integral is divergent.
Q4: Find out the integral  is convergent or divergent. Find the value in case of convergent.
is convergent or divergent. Find the value in case of convergent.
A4. Follow the same process as we did above,
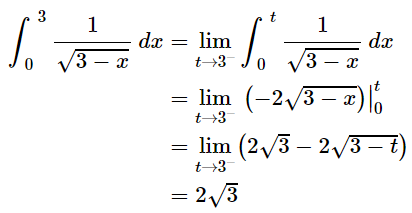
Here limit exists and finite , so that the integral is convergent. And its value is 2√3.
Q5: Evaluate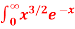 dx
dx
A5: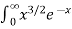 dx =
dx = 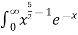 dx
dx
= γ(5/2)
= γ(3/2+ 1)
= 3/2 γ(3/2 )
= 3/2. ½ γ(½ )
= 3/2. ½ π
= ¾ π
Q6: Evaluate 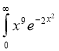 dx.
dx.
A6: Let 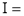
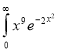 dx.
dx.
x | 0 |
|
t | 0 |
|
Put 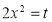 or
or 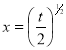 ; 4x dx = dt
; 4x dx = dt
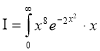 dx
dx

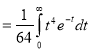
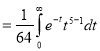
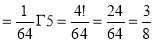
Q7: Evaluate I = 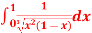
A7:

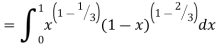
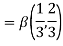
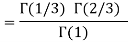
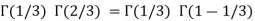
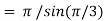
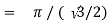
= 2 π/3
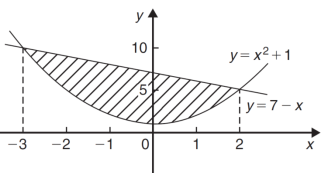
Q8: Determine the area enclosed by the curves-

A8:. We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-
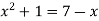
Which gives-
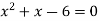
By factorization,
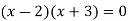
Which means,
x = 2 and x = -3
By determining the intersection points the range the values of x has been found-
x | -3 | -2 | -1 | 0 | 1 | 2 |
| 10 | 5 | 2 | 1 | 2 | 5 |
And
x | -3 | 0 | 2 |
y = 7 - x | 10 | 7 | 5 |
We get the following figure by using above two tables-
Area of shaded region = 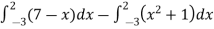
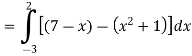
= 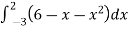
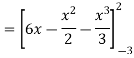
= ( 12 – 2 – 8/3 ) – (-18 – 9/2 + 9)
= 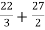
= 125/6 square unit
Q9: Find the area enclosed by the curves  and if the area is rotated
and if the area is rotated  about the x-axis then determine the volume of the solid of revolution.
about the x-axis then determine the volume of the solid of revolution.
A9: We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-
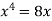
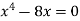
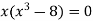
We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
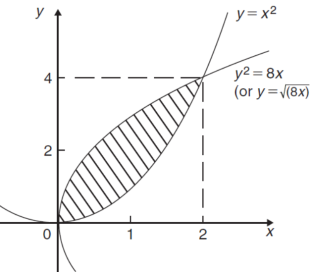
Then,
The area of the shaded region will be-
A = 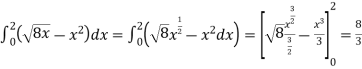
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving  – (volume produced by revolving
– (volume produced by revolving 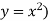
= 
Q10: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0 , 2].
A 10:. The graph of the function f(x) = 2x - x² will be-
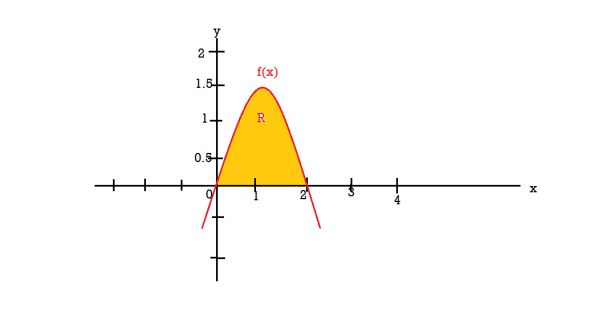
The volume of the solid is given by-
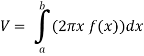
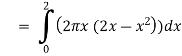
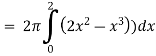
=