Unit-3
Design of one way slab
Q1) Explain one way slab
A1) The slab which is supported on two opposite support is called as one way slab.
When the aspect ratio (ly / lx) is greater than 2, the slab is called as one way slab.
Aspect ratio =ly /LX > 2
Where, lx = length of shorter span
ly= length of longer span
It bends in one direction only.
Main reinforcement is provided to the shorter span only.
Distribution steel is provided is along the transverse direction to hold the main steel in position and take care of shrinkage and temperature stresses.
General Specifications for Slabs in I S 456: 2000
1) Effective Span:
The effective span of a slab depends upon the boundary condition as per IS456: 2000: clause No. 222 page No. 34.
Simply supported slab or beam which is not built integrally with its support
l = Clear span + effective depth
l = Clear span + width of support, …….. whichever is less
Cantilever slab.
Effective span = length to the face of support + effective depth
Le = L + d/2
2) Modification Factor (M.F):
Span to effective depth ratio: (Ref. IS456: 2000: clause page No, 37)
Basic value of span to effective depth ratio for spa 10 m.
b) For spans above 10 m. the value in (a) may be multiple by 10/span is meters, except for cantilever.
c) Depending on the area and the stress of steel for tension reinforcement, the value in (a) and (b) shall be modified by multiple with modification factor
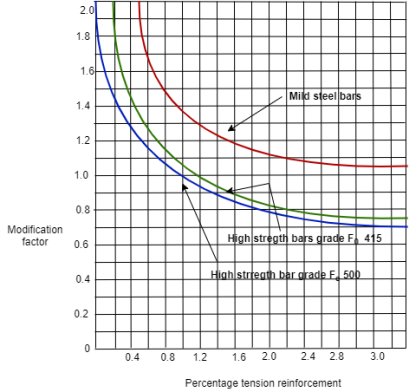
Fig no 1 Percentage tensile reinforcement
d = …….. For simply supported slab (one way)
d = …….. For cantilever slab
Reinforcement requirements for slab
1. Minimum reinforcement
2. Maximum diameter of reinforcing bar
3. Maximum distance between bar in tension (spacing)
4. Control of deflection
1) Minimum reinforcement:
As per clause 26.5.2.1, page no. 48 of IS456: 2000, reinforcement in each direction should not exceed as given below,
Type of reinforcement | Percentage steel |
Mild steel | 0.15% of total cross section area |
Hysd | 0.12% of total cross section area |
2) Maximum diameter of reinforcing bar (clause 26.5.2.2):
Diameter of bar <
3) Maximum distance between bar in tension (spacing)
As per clause 26.3.3(b), page no. 46 of IS456: 2000, spacing of reinforcement in each direction should not exceed as given below
Main reinforcement < 3 x effective depth of slab or 300 mm whichever is less.
Steel for shrinkage and temperature (distribution steel) < 5 x effective depth of slab or 450 mm whichever is less.
4) Control of deflection:
As per clause 23.2(b), page no. 37 of IS456: 2000, deflection of slab should not exceed span /350 or 20 mm whichever is less.
Q2) What are steps of design simply supported one way slab
A2)
Design steps of Simply Supported One-way Slab
One-way slab is designed as a rectangular beam of one metre width in cross-section; as a balanced section to satisfy the requirements of limit state of collapse in flexure.
Step 1: Type of slab
(i) Aspect ratio =l y /lx > 2, it is one way slab
(ii) According to support condition, it may be simply supported, cantilever or continuous slab.
Step 2: Depth of slab based on deflection criteria (cl. 23.2, page No. 37).
Sr no | Type of slab | Basic value |
1 | Cantilever | 7 |
2 | Simply support | 20 |
3 | Continuous | 26 |
Assume percentage of steel find out modifications Factor for given of steel.
Grade of steel | Design stress | Percentage steel |
Fe 250 | 145 | 0.7% to 1% |
Fe 415 | 240 | 0.25% to 0.45% |
Fe 500 | 290 | 0.2% to 0.35% |
Depending on the area and the stress of steel for tension reinforcement, the values in (a) and (b) shall be modified by multiplying with modification factor obtained as per below figure.

Fig no 2 Percentage tension reinforcement
Depending on the area of compression reinforcement the value of span to depth ratio be further modified by multiplying with the modification factor obtained as per below figure.

Fig no 3 Percentage compression reinforcement
d = …….. For simply supported slab (one way)
d = …….. For cantilever slab
Step 3: Find the effective span of the slab (Clause 22.2 of IS456: 2000 page 34)
The effective span of a member that is not built integrally with its supports shall be taken as clear span plus the effective depth of slab or to centre of supports whichever is less.
L effective= clear span + effective depth
OR
L effective= centre to centre of supports. ..........whichever is less.
Step 4: Load calculation
1) Dead load: refer IS875: 1984 (Part 1)
The self weight of slab may be found by considering unit area of slab and thickness of slab.
Self weight of slab = unit weight of concrete x depth of slab
Live load: refer IS875 : 1984 (Part 2)
Total load to be supported by slab per unit length along the short span is obtained.
3) Floor Finish (FF)
In addition to this also consider the weight of floor finish i.e. 0.6 to 1 kN/m2
Total load w = (DL + LL+ FF)
Factored load wu = Load factor x Total load
= 1.5 w
Step 5: Design factored moment
For cantilever slab,
Mu = 0.87fyAst(d – 0.42xu)
For simply supported slab,
Mu =
Step 6: check for depth of slab
Grade of steel | Mu limiting |
Fe 250 | 0.148 f CK b d2 |
Fe 415 | 0.138 f CK b d2 |
Fe 500 | 0.133 f CK b d2 |
(OR) using relation Mu = 0.36fck• xu • b (d - 0.42 xu) where xu = xulim
Equate factored bending moment of Mu lim
If drequired<dassumed safe for flexure.
Overall depth = depth + clear cover
Step 7: Main reinforcement
Ast = 0.5 fck/ fy (1- √ 1- ((4.6 Mu)/(f CK b d 2)) b d
Or
Ast is calculated from the equation.
Mu = 0.87 fyAst(d – 0.42xu)
Step 7.1: check for minimum reinforcement
Type of reinforcement | Percentage steel | Ast min per meter |
Mild steel | 0.15% of total cross sectional area = 0.15 % bD | 1.5 D |
HYSD | 0.12 % of total cross section area = 0.12% b D | 1.2 D |
Where D = overall depth of slab
Step 7.2: Maximum diameter
Ref. Clause 26.5.2.2 of IS456: 2000, page number 48
d should not be less than
Assume diameter of bar 8 mm or 10 mm or 12
Step 7.3: Spacing of main reinforcement
Spacing, s = 1000 ast/Ast
Where ,ast = Area of one bar.
Check or maximum spacing for main reinforcement
Spacing , s = 3d Or 300 mm ………………..whichever is smaller
Step 8: Check for serviceability
Calculate actual percentage of steel provided.
Pt = x 100
Find actual modification factor corresponding to given grade of steel and point actul
Depth required ( for deflection) =
Depth required must be less than d provided. If not then the effective depth must be increased.
Step 9: Distribution steel
Minimum area of steel in tension is provided as distribution steel.
Assume diameter of bar 6 mm for Mild steel or 8 mm for HYSD bar.
Spacing = 1000 ast/Ast
Check spacing < 5d or 450 mm whichever is less.
Step 10: Check for development length
Provided development length L d and value of from cl.26.2.1, page No. 42 of IS456.
Ld= Lo + d/2
Where , d = diameter of bar
The value of 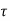 bdis increased by 60 % for deformed bar.
bdis increased by 60 % for deformed bar.
Permissible development length :
L d ≤ 1.3 + Lo
Reinforcement should be extend from the face of support by length equal to.( Ref. cl. 26.2.3.3a).
M1 = Moment of resistance of remaining bar at support
= Tu1 x z = 0.87 fy Ast1 (d - 0.42 xu)
Ast= area of bar at supports (half of the area at the centre).
Vu = Shear force at centre of support.
Provided development should not exceed with limited development
Step 11: Check for shear
Calculate, 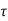 v =
v =
From Table 19 of IS456 : 2000 page 73 find the design shear strength of concrete considering grade of concrete and percentage of steel.
Further multiply this design shear strength by k (clause 40.2.1.1 page 72 of IS456 : 2000) to get exact design shear strength. This should not be less than 𝜏v calculated above.
Note:
The shear force in slab is very small and there is no need to provide shear reinforcement in slab.
Step 12: Details of reinforcement
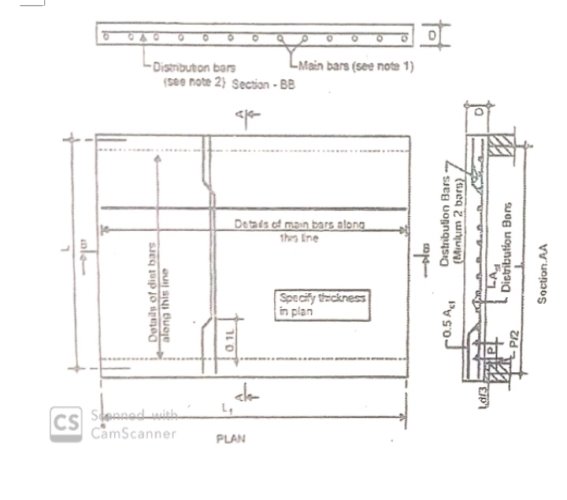
Fig no 4 Reinforcement
Note:
Diameter 8 mm for deformed bars 10 mm for plain bars: spacing not more than 3d or 300 mm
Diameter 6 mm spacing not more than 5d or 450 mm ( Typical details of a slab spanning in one direction i.e. one way slab)
Q3) Design of simply supported slab one way slab:
Design a simply supported slab for a room with clear inner size 3 mx 7 m. The slab is supported by beams of width 230 mm along all the edges. The slab is subjected to floor finish of 1 kN/m2and live load 4 kN/m2.Use concrete of grade M20 and Fe 500 reinforcement. Draw details of reinforcement. Check for shear is not required. (Use LSM).
A3)
Step 1: Aspect ratio = ly/LX = 2.33 > 2 ……….It is a one way slab
Step 2: Trial depth of the slab
For shorter span 3m > 3.5m, Ref. Clause 23.2.1 of IS 456:2000
Assume percentage steel 0.3 %, modification factor is 1.25 For Fe500
D required = 120 mm
Assuming cover 15 mm and diameter of bar 10 mm
D = d + c + d/2
= 120 + 15 + 10/2
= 140 mm
Step 3: Calculate efficiency span l effective
L effective= L + d
= 3 + 0.12 = 3.12 m
L effective= L + b
= 3 + 0.23 = 3.23 m
L effective = 3.12 m ………… whichever is less
Step 4: Load calculation:
Self weight = 0.14 x 1 x 25 = 3.5 KN/m
F.F = 1 KN/m
L.L = 4 KN/m
Total = 8.5 KN/m
Factored load = 1.5 x 8.5 = 12.75 KN/m
Step 5: Factored moment:
Mu = 15.51 KN m
Factored shear force
Vu = 19.89 KN
Step 6: Determine required depth of bendng:
For Fe500
Mu.lim = 0.133fckbd2
15.51 x 106= 0.133x 20 x 1000d2
d = 76.35 mm < 120 mm
If d required<d assumed …………….. safe for flexure.
Step 7: Determine main steel:
A s t = 0.5fck/f y(1-√1-((4.6Mu)/(fCKbd2))b d
A s t = 318.39 mm2
Spacing of 10 mm diameter of bar
Spacing, s = 1000 a s t/A s t
s = 246.67 = 240 mm c/c
Check, s < 3d
240 < 300 ………………..ok
Provided main reinforcement of 10 mm diameter of bar @ 240 mm c/c
Pt actual = 0.26 % >0.12 %
Step 8: Determination of distribution steel:
Assuming 6 mm diameter bar is used for distribution steel
Ast d = 0.12 % of A gross = 0.12 % bD
Ast d = 0.12 x 1000 x 140
= 168 mm2
Spacing of distribution steel
Spacing, s = 1000 a s t/A s t
s = 168.299 = 160 mm c/c
Check for max spacing
S < 5d = 5 x 120 = 600 mm
S = 160 mm ……………. Ok
Provided distribution reinforcement of 6 mm diameter of bar @ 160 mm c/c
Step 9: Check for deflection
F s = 0.58 f y
A s t required = 318.39 mm2
A s t provided = 327.08 mm2
F s = 0.58 x 500 x
= 282. 29 mm2
Actual modification factor for pt = 0.26 % and for Fe500 is 1.2 ( as per fig 0f modification factor of tension reinforcement)
Depth required (For deflection) = span/20 MF
Depth required (For deflection) = 125 mm
As D required for deflection < D required
125 mm< 140 mm ……………..ok
Q4) Design a cantilever chajja slab projecting 1.5 m, from the support using M-20 grade concrete and Fe415 steel. Take L.L as 2kN/m2. And F.F is 2 kN/m2
A4)
Step 1: Trial depth of slab 'D'
Assuming M.F. = 1.5
D required =142.8 mm
Assuming cover 15 mm and diameter of bar 8 mm
D = d + c + d/2
= 142.8 + 15 + 8/2
= 161.85 mm = 170 mm
Effective depth d = D – c – d/2
= 170 – 15 – 8/2
= 151 mm
Step 2: Load calculation:
Self weight = 0.17 x 1 x 25 = 4.25 KN/m
F.F = 2 KN/m
L.L = 2 KN/m
Total = 8.25 KN/m
Factored load = 1.5 x 8.25 = 12.375 KN/m
Step 3: Factored moment:
Mu = 13.92KN.m
Step 4: Determine required depth of bendng:
For Fe415
Mu.lim = 0.138fckbd2
13.92 x 106= 0.138x 20 x 1000d2
d = 71mm < 151 mm
If drequired<dassumed …………….. safe for flexure.
Step 5: Determine main steel:
As t = 265.11 mm2
A s t d = 0.15 % of A gross = 0.15 % bD
A s t d =0.15 x 1000 x 170
A s t d= A s t min = 255 mm2
Spacing of 8 mm diameter of bar
Spacing, s = 1000 a s t/ A s t
s = 189.35 = 180 mm c/c
Provided main reinforcement of 8 mm diameter of bar @ 180 mm c/c
check , s < 3d
180 < 453 ………………..ok
Provided main reinforcement of 8 mm diameter of bar @ 180 mm c/c
Step 6: Determination of distribution steel:
Assuming 6 mm diameter bar is used for distribution steel
A s t d = 0.15 % of A gross = 0.15 % bD
A s td = 0.15x 1000 x 170
= 255 mm2
Spacing of distribution steel
Spacing, s = 1000 a s t /A s t
s = 110.8 = 150 mm c/c
Check for max spacing
S < 5d
S = 150 mm ……………. Ok
Provided distribution reinforcement of 6 mm diameter of bar @ 150 mm c/c
Step 7: Check for deflection
F s = 0.58 f y A s t required/A s t provided
A s t required = 265.11 mm2
A s t provided = 278.88 mm2
F s = 0.58 x 415 x 265.11/278.88
= 228.8 mm2
Pt actual = 0.186 % > 0.12 %
Actual modification factor for pt = 0.185% and for Fe415 is 1.8( as per fig 0f modification factor of tension reinforcement)
Depth required (for deflection) = 119 mm
As D required for deflection < D required
119 mm< 151 mm ……………..ok
Step 8: check for development L d
L d= 1.92 N/mm2for M20 concrete
Ld= 376 mm
L d = 1.3 + Lo
Providing 90° bend and clear cover of 25 mm at side end
Assume support width = 300mm
Lo = – side cover – 3 x diameter of bar
= – 25 – 3 x 8
= 149 mm
Md = 13.92 x 106 N.mm
Vd = Wu x L
= 12.375 x 1.5 = 18.56 KN
L d = 1.3 + Lo
L d = 1.3 +149
L d =1779.5 mm
L d ≤ 1.3 + Lo
376 ≤ 1779.5 mm …………….ok
Fig no 5 Detailing
Q5) Explain the design steps of one way continuous slab
A5) Design Step for Continuous Slab
Continuous slab are design by using moment and shear coefficients given in table 12 and 13 page no.36 of IS456:2000.
Step 1: Effective span
As per clause 22.2., Page no. 34 and 35 of IS456: 2000
When b w<
Effective span L = Clear span + effective depth
L = Clear span + width of support …………. whichever is less
When b w>or 600 mm whichever is less, effective 12 span for end span with one end fixed and the other end is continuous or for intermediate spans shall be taken as
Effective span = Clear span between supports
Step 2: Load calculation
W d = Factored dead load
= 1.5 (Dead load + floor finish)
WL = Factored live load
= 1.5 LL
Step 3: Factored bending moment
Clause 22.5.1, Table 12 Page No. 36 of IS456: 2000
Note:
For obtaining the bending moment, the coefficient shall be multiplied by the load design load and effective span.
(A) Span moment:
1) B. M. near middle of end span M1
M1 = w d Le2 + w L Le2
2) B. M. at middle of interior span M2
M2 = w d Le2 + w L Le2
(B) Support moment:
B. M. at support next to end support
M3 = - w d Le2 – w L Le2
B. M. at other interior support
M4 = - w d Le2 – w L Le2
Step 4: Check for required depth
Equating maximum B.M. to Mu limiting
Step 5: Main Reinforcements
A s t= 0.5fck/f y (1-√1-((4.6Mu)/ (fCKbd2))b d
Step 6: Distribution Reinforcements
Type of reinforcement
Mild steel = 0.15 % of total cross sectional area = 0.15 % b D
HYSD = 0.12 % of total cross sectional area = 0.12 % b D
Step 7: Check for deflection:
Pt actual=FS x 100
F s = 0.58 f y A s t required/ A s t provided
Based on percentage steel and design stress from Fig. 4 page no.38, of IS456: 2000, Actual Modification factor is calculated.

Fig no 6 Percentage tension reinforcement
Depth required (for deflection) =
As D required for deflection < D required
Step 8: check the shear:
Note:
For obtaining the shear force the coefficient shall be multiplied by the total design load.
Shear force at end:
Vu = 0.4 w d Le + 0.45 WL L e
2) Shear force at support next to the end support:
a) Outer side
Vu = 0.6wd Le + 0.6 WL L e
b) Inner side
Vu = 0.55wd Le + 0.6 WL L e
3) Shear force at all interior supports:
Vu = 0.5 w d Le + 0.6 WL L e
Select the maximum shear force calculated
Nominal shear stress  v =
v =
From Table 19 of IS456: 2000 page 73 find the design shear strength of concrete considering grade of concrete and percentage of steel.
Further multiply this design shear strength by k (clause 40.2.1.1 page 72 of IS456: 2000) to get exact design shear strength. This should not be less than 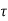 v calculated above.
v calculated above.
Q6) Design a continuous slab to cover a hall 8 m x 17.5 m. The live load on a slab is 3.5 k N/m2 floor finish 0.8 k N/m2. Use M20 concrete and Fe415 steel. The slab is monolithically construction with beams & spaced at 3.5 m centre to centre.
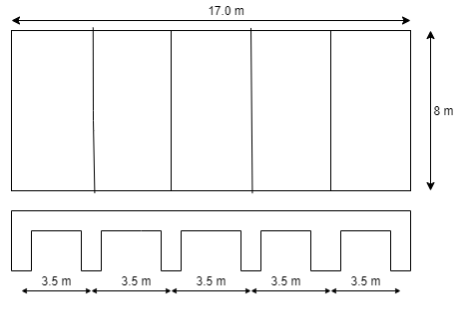
Fig no 7 Given figure
A6)
Step 1: Aspect ratio = 2.29> 2 ……….It is a one way slab
Step 2: Trial depth of the slab
Assume percentage steel 0.35%, modification factor is 1.4 For continuous slab
D required = 96.15 mm
Assuming cover 15 mm and diameter of bar 10 mm
D = d + c + d/2
= 96.15+ 15 + 10/2
= 120 mm
D = 120 – 20 = 100mm
Step 3: Effective span:
Assume support width is 300mm
= 250mm <bw>
L = Clear span + width of support
L = 3500 – 300
= 3200 mm
Step 4: Load calculation:
Consider load per unit width
D.L = 25D = 25 x 0.12 = 3 KN/m
F.F = 0.8 KN/m
DL + imposed fixed load = 3.8 KN/m
Factored load wd = 1.5 x 3.8 = 5.7 KN/m
LL (imposedl s not fixed) = 3.5 KN/m
Factored load wL = 1.5 x 3.5= 5.25 KN/m
Step 5: Factored bending moment:
(A) Span moment:
1) B. M. near middle of end span M1
M1 = w d Le2 + wL Le2
M1 = 5.71 x 3.32 + 5.25 x 3.22
M1 = 10.25 KN m
2) B. M. at middle of interior span M2
M2 = w d Le2 + wL Le2
M2 = 5.71 x 3.32 + 5.25 x 3.22
M2 = 8.13 KN m
(B) Support moment:
B. M. at support next to end support
M3 = - w d Le2 – w L Le2
M3 = - 5.71 x 3.32 - 5.25 x 3.22
M3 = 11.81 KN m
B. M. at other interior support
M4 = - wd Le2 – wL Le2
M4 = - x 5.71 x 3.32 - 5.25 x 3.22
M4 = 10.84 KN m
Maximum B.M, BM max = 11.31 x 106 N.mm
Step 6: Check depth:
For Fe415
Mu.lim = 0.138fckbd2
11.81 x 106= 0.138x 20 x 1000d2
d = 65.4 mm < d provided ……………ok
Step 7: steel reinforcement:
Xulimiting= 0.48d = 0.48 x 100 = 48 mm
Mulimiting = 0.36 fckxulimiting .b ( d – 0.42 xulimiting)
= 0.36 x 20 x 48 x 1000 ( 100 – 0.42 x 48)
= 27.6 x 106 > 11.81 x 106
Hence design slab as singly reinforced under reinforced
A s t d = 0.12 % of A gross = 0.12% bD
A s t d = 0.12 x 1000 x 120
= 144mm2
A s t for mid of end span for M1
Ast1 = 302.78 mm2
Spacing of 8 mm diameter of bar
Spacing,
s = 166 = 160 mm c/c < (3d or 300mm) ………ok
A s t provided = 314.3 mm2
A s t for middle of interior span for M2
Ast2= 236.94 mm2
Spacing of 8 mm diameter of bar
Spacing, s = 1000 A s t/ A s t
s = 212 = 210 mm c/c < (3d or 300mm) ………ok
A s t provided = 239 mm2
As t for at support next to end support for M3
Ast3 = 353 mm2
The alternate bar for mid span will bent up at 0.25 L
= 0.25 x 3500 = 875 mm from centre of support
Extended for length = 0.3L = 0.3 x 3500 = 1050 mm from face of support
Area of bent up bar =
Area of steel available bent up bar = 276.5 mm2
Required A s t = A s t 3= A s t available = 353 – 276.5 = 76.5 mm2
Spacing of 8 mm diameter of bar
Spacing,
s = 657 = 600 mm c/c < n ( 3d or 300mm) ………ok
A s t for interior support for M4
Ast3 = 322mm2
Steel available due to alternate bent up bar
Area of bent up bar =
Area of steel available bent up bar = 239 mm2
Required A s t= A s t 3 = A s t available = 322 – 239 = 83mm2
Spacing of 8 mm diameter of bar
Spacing,
s = 605.5 = 600 mm c/c <( 3d or 300mm) ………ok
Provided 8 mm diameter extra bar at 600 mm c/c for length pf 0.3 L = 0.3 x 3500 = 1050 mm from the face on both sides of support
Step 8: Determination of distribution steel:
Assuming 6 mm diameter bar is used for distribution steel
A s t d = 0.12 % of A gross = 0.12 % bD
A s t d = 0.12 x 1000 x 120
= 144 mm2
Spacing of distribution steel
Spacing, s= 1000 a s t/ A s t
s = 196.3 mm = 190 mm c/c
Check for max spacing
S < 5d
S = 190 mm ……………. Ok
Provided distribution reinforcement of 6 mm diameter of bar @ 190 mm c/c
Step 9: Check for serviceability:
Actual modification factor for pt = 0.3% and for Fe415 is 1.3 (as per fig 0f modification factor of tension reinforcement)
Depth required (for deflection) = 94.32 mm
As D required for deflection < D required
94.32 mm< 100 mm ……………..ok
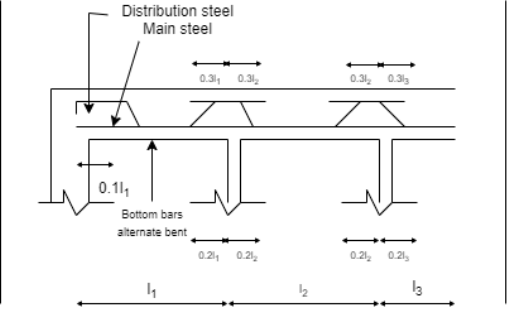
Fig no 8 Detailing reinforcement
Q7) Design the first flight of a dog legged staircase for the following data:
(a) Centre line dimensions of staircase room = 2.5 m x 4.75 m;
(b) Floor to floor height = 3.0 m;
(c) Rise = 150 mm; Tread = 300 mm
(d) Width of landing = 1.25 m;
(e) Live load = 3 k N/m2 and Floor Finish = 1 k N/m2
(f) Material M 20, Fe 500.
Draw neat sketch showing details of reinforcement.
A7)
Step 1: Preliminary data:
Height of each flight H: = 1500 mm
Number of riser R = floor to floor height / 0.15 = 10
Number of treads T: R – 1 = 10 – 1 = 9
Going G = Number of tread x tread = 9 x 300 = 2700 mm
Landing on each side = 1.025 m
Length of first flight:
L1 = Going + landing = 2700 + 1025 = 3725 mm
Step 2: Depth of waist slab based on serviceability:
Assume percentage steel 0.4 %, modification factor is 1.1 For Fe 500(Ref fig 4, page 38 of IS 456 – 2000)
Fs = 0.58 fy = 0.58 x 500 = 290 mpa
L/ d = 20 M.F
D required = 169.3 mm
Assuming cover 15 mm and diameter of bar 10 mm
D = d + c + d/2
= 169.3 + 15 + 10/2
= 189.3 mm, say 200 mm
d = D – c – d/2 = 200– 15 – 10/2 = 180mm
Step 3: Calculate efficiency span l effective
L effective = Lx + d or l effective = Lx + b ……………. whichever is less
L effective= Lx + d
= 3.725 + 0.180= 3.9 m
L effective= 3.9 m ………… whichever is less
Step 4: Load calculation:
D.L of waist slab = D x γ
= 0.2 x 20
= 4.47 kN/m2
L.L= 3 kN/m2
F.F = 1 kN/m2
Total (w1)= D.L of waist slab + L.L + F.F
= 4.47 + 3 + 1
= 8.47 kN/m2
Self weight of step = γxload
= 20 * load
= 1.5 kN/m2
Total (w2) = w1+ Self weight of step
= 8.47 + 1.5
= 9.97 kN/m2
Step 5: Factored load:
Wu1 = 1.5 x w1 = 1.5 x 8.47 = 12.7 kN/m
Wu2 = 1.5 x w2 = 1.5 x 9.97 = 12.7 kN/m
Step 6: Factored bending moment:
Consider maximum loading throughout the span:
Mu = 28.52 KN m
Step 7: Depth required for maximum bending moment:
Mu= Mu.lim
For Fe500
Mu.lim = 0.133fckbd2
28.52 x 106= 0.133x 20 x 1000d2
d = 103.54 mm < 180mm
If drequired<dassumed …………….. safe for flexure
Step 8: Determine main steel:
A s t= 385 mm2
Check of minimum A s t
A s t min = 0.12 % of A gross = 0.12 % bD
A s t min = 0.12 x 1000 x 200
= 240 mm2
A s t>A s t min ………….….ok
Spacing required for A s t
Spacing of 10 mm diameter of bar
Spacing, s = 3 d or 300 mm
s = 204 mm = 200 mm c/c
Check, s < 3d or 300mm
200 < 540 ………………..ok
Provided main reinforcement of 10 mm diameter of bar @ 200 mm c/c
Step 9: Distribution steel:
A s t min = 0.12 % of A gross = 0.12 % bD
A s t min = 0.12 x 1000 x 200
= 240 mm2
Spacing required for A s t min
Spacing of 6 mm diameter of bar
Spacing, s = 1000 a s t/ A s t
s = 117.8 mm = 110 mm c/c
Check, s < 5d or 450mm
110 < 900………………..ok
Provided distribution reinforcement of 6 mm diameter of bar @ 110 mm c/c
Step 10: Check for deflection
F s = 0.58 f y A s t required /A s t provided
A s trequired = 385mm2
A s tprovided = 0.12 % b D
A s tprovided = 392.7 mm2
Service stress:
F s = 0.58 f y
F s = 0.58 x 500
= 284 mm2
Percentage of steel:
Pt actual = 0.22% > 0.12 %
Modification factor
Actual modification factor for pt = 0.22% and for Fe500 is 1.4(as per fig 0f modification factor of tension reinforcement)
Depth required for deflection
B M max = 0.138 f c k bd2
Depth required (for deflection) = 139.3 mm
As D required for deflection < D required
139.3 mm< 180 mm ……………..ok
Safe in deflection
Q8) What are the design steps of lintel and chjjas
A8)
DESIGN OF LINTEL AND CHAJJAS
The steps of RCC lintel design (single span or continuous with a few openings) are same as the design of a simple beam
1. The lintel width is equal to the wall thickness
2. Consider a suitable depth of the lintel
3. Choose the effective span of the lintel (consider reasonable end bearing and effective depth)
4. Let W be the aggregate weight of the masonry work encased in the triangle in the event that conditions warrant load of the workmanship on the lintel
5. Calculate the maximum bending moment (M1) at the centre of the lintel (due to the triangular load)
M1 = WL/6
6. Now calculate the maximum bending moment (M2) due to the self weight (w) of the lintel per meter length
M2 =w l^2/8
7. Total maximum bending moment at the center of the lintel is
M = M1 +M2 = WL/6 + w l^2 /8
8. Find out the effective depth (d) of the lintel by using the given formula
d = (M/Q ×b)
9. Now calculate the area of steel (A s t)
A s t = M/t × JD
Give this zone in a type of appropriate diameter bars .Twist around 40% -50% steel rods up at 1/7 distance from lintel end
10. Calculate maximum shear force= W/2 + WL/2
11. Finally, check the lintel in shear and development length
12. Give 6 mm  two legged ostensible stirrups at most extreme c/c spacing of the lever arm (JD)
two legged ostensible stirrups at most extreme c/c spacing of the lever arm (JD)
Q9) Design a RC slab for a store room having clear dimensions as 4.77m x 3.77 m. The slab is to be casted monolithically over the 230mm wide beam with corners of slab held down. The slab carries live load of 3 k N/m2 and floor finish of 1 k N/m2Use M20 grade of concrete and Fe415 grade of steel. Also show details of reinforcement.
A9)
Given:
Longer span l y = 4.77 m.
Support beam width b s = 230 mm.
Shorter beam lx = 3.77 m.
Condition: corners of slab held down
Live load LL = 3 k N/m2,
M20 Fe 415
Floor finish FF = 1 k N/m2
F c k = 20 N/mm2
F y = 415 N/mm2
Solution
Step 1: Aspect ratio: =l y /LX = 1.265 < 2 ……….It is a two way slab
Step 2: Trial depth of the slab
For shorter span 3.77> 3.5m, Ref. Clause 23.2.1 of fig – 4, of IS 456:2000 so that lx/d ratio given in clause 24.1 is not applicable.
Assume percentage steel 0.3 %, modification factor is 1.45 For Fe500
Fs = 9.58 f y = 0.58 x 415 = 240 m pa
D required = Span /20 MF
D required = 130 mm
Assuming cover 15 mm and diameter of bar 8 mm
D = d + c + d/2
= 130 + 15 + 8/2
= 149 mm
d = D – c – d/2 = 150 – 15 – 8/2 = 131mm
Step 3: Calculate efficiency span l effective
L effective = Lx + d
= 3.77 + 0.131= 3.901 m
L effective = Lx + b
= 3.77 + 0.23 = 4 m
L effective = 3.9 m ………… whichever is less
Step 4: Load calculation:
Self weight = 0.15 x 1 x 25 = 3.75 KN/m
F.F = 1 KN/m
L.L = 3 KN/m
Total = 7.75 KN/m
Factored load = 1.5 x 7.75 = 11.625 KN/m
Step 5: Factored moment:
M x = α x w L2x
My = α y w L2x
Since the slab is monolithically casted with corners of slab held down ( Ref : IS 456 – 2000 , table 26 , case 9 )
Four edges discontinuous
Ly/ lx |
|
|
1.2 | 0.072 | 0.056 |
1.3 | 0.079 | 0.056 |
 x= 0.072 + ((0.079- 0.072)/ (1.3- 1.2)) (1.265 – 1.2 ) = 0.076
x= 0.072 + ((0.079- 0.072)/ (1.3- 1.2)) (1.265 – 1.2 ) = 0.076
Α y = 0.056
Mu x = 0.076 x 11.625 x (3.9)2= 13.54 KN m
M u y = 0.056 x 11.625 x (3.9)2= 9.89 KN m
Mu max = 13.54 KN m
Step 6: Determine required depth of bending:
For Fe415
Mu.lim = 0.138fckbd2
13.54 x 106= 0.138x 20 x 1000d2
d = 70 mm < 131mm
If d required<d assumed…………….. safe for flexure.
Step 7: Determine main steel:
Shorter span:
A s t x = 0.5 f c k/ f y (1- √ 1- ((4.6 Mu)/(f CK b d 2)) b d
A s t x = 300 mm2
Longer span:
d = (131 – 8) = 123 mm
A s t y= 0.5fck/f y(1-√1-((4.6Mu)/(fCKbd2))b d
A s t y = 232 mm2
Minimum area of steel in tension for HYSD
A s t min = 0.12 % of A gross = 0.12 % b D
A s t min = 0.12 x 1000 x 150
= 180 mm2
Both A s t x and A s t y>A s t min ………….….ok
Step 8: Spacing:
Spacing required for A s t x
Spacing of 8 mm diameter of bar
Spacing, s = 1000 a s t / A s t
s = 167.6 = 160 mm c/c
check, s < 3d or 300mm
160 <393………………..ok
Provided main reinforcement of 8 mm diameter of bar @ 160 mm c/c
Spacing required for A s t y
Spacing of 8 mm diameter of bar
Spacing, s = 1000 a s t / A s t
s = 216.6 = 210 mm c/c
Check, s < 3d 04 300mm
210 < 393 ………………..ok
Provided main reinforcement of 8 mm diameter of bar @ 210 mm c/c
Step 9: Torsion steel:
Clause D – 1.8 page no. 90. IS 456: 2000
As the corner of the slab held down (I e torsion restrained at corner), corner reinforcement has to provided in form meshes at top and bottom at each corner.
Side of mesh = LX / 5=3900/5 = 780 mm
Area of steel in each layer = 3/7 A s t x= 3/7 x 300 = 225 mm2
Spacing, s = 1000 a s t /A s t
s = 125 mm c/c
Provided 4 – 8 mm diameter bar both at top and bottom at each corner
Step 10: Check for deflection
F s = 0.58 f y area of steel required/ area of steel provided
A s t required = 300mm2
A s t provided = 1000 a s t / S required
A s t provided = 314.16 mm2
F s = 0.58 x 415 x (300/314.16)
= 230 mm2
Pt actual= x 100
Pt actual = A s t /BD x 100
Pt actual = 0.24% > 0.12 %
Actual modification factor for pt = 0.24% and for Fe415 is 1.65 (as per fig 0f modification factor of tension reinforcement)
Depth required (for deflection) = span /20 MF
Depth required (for deflection) = 118.2 mm
As D required for deflection < D required
118.2 mm< 131 mm ……………..ok
Slab is safe in deflection
Fig no 9 Reinforced detailing
Q10) Explain cracking and vibration
A10) CRACKING
1. Decreased plastic cracking of the plastic
When the concrete is in its plastic state (before hardening), it is filled with water. When that fluid finally leaves the sieve, it leaves behind large gaps between the solid particles. These blank spaces make the concrete fragile and more prone to cracking. This type of cracking occurs more frequently and is called "plastic shrinkage cracking".
While sloping plastic cracks can occur anywhere on the slab or wall, they almost always occur in intersecting corners (corners pointing to the slab) or with circular objects between slides (pipes, plumbing fixtures, drains and holes). Since the concrete will not sink into the corner, the pressure will cause the concrete to crack from the location of that corner cracks in plastic shrinkage
Decreased plastic cracks are usually very small in width and invisible. While it is almost invisible, it is important to remember that cracks in plastic shrinkage not only affect the surface, they extend to the entire size of the lab.
Excessive wet mixing is a contributing factor to the reduction of concrete. While water is an important ingredient in any concrete mix, there is such a thing as too much water. When the mixture contains too much water, the slab will shrink beyond the use of the right amount of water. The hot weather is another major cause of cracks in plastic decay.
Control joints can be inserted into the slide to prevent shrinkage cracking. The joints will open as the concrete lump becomes smaller.
2. Expansion of concrete cracks
Expansion cracks
Like a balloon, heat causes the concrete to expand. As the concrete expands, it presses on anything in its path (a brick wall or a nearby slab). When there is no flexibility, growing strength may be enough to cause concrete.
Extension joints are used as a point of separation (or separation), among other fixed areas. Often made of compact materials such as asphalt, rubber, or wood, the expansion joints must act as shock absorbers to relieve stress extensions that include concrete and prevent cracks.
3. Reduction of concrete cracks
Cracks burst
When the soil is cold, you can sometimes lift several inches before melting and sitting down. The movement of the earth brought about by the cycle of freezing and thawing is a major factor in the cracking of concrete. If the slab does not have freedom of movement, the slab will crack.
The roots of large trees can have a similar effect on a slide. If the tree is too close to the slab, the growing roots can lift and crack the concrete. Always keep this in mind when you put the label on.
4. Repairing concrete cracks
To repair cracks
On the other hand, sitting on a concrete slide can also cause cracks.
Fixing cracks occurs in cases where a gap is created in the soil beneath the concrete. Imagine when a large tree is removed near the roots begin to rot or when the company used to dig a trench for their ropes, pipes, etc. repairing cracks is possible.
5. Crack of concrete caused by overcrowding of the slide
Overloading cracks
Although concrete is a very durable material, it has its limitations. Putting too much weight on a concrete slide can cause cracks. If you feel the concrete mix is stronger than 2000, 3000, 4000, or 5000 + PSI, it refers to the kilograms per square inch that can take to crush that concrete slab.
When it comes to concrete tabs that reside, real overload slides are not all that. Instead, it is likely to occur in excess of the ground under the slide.
After heavy rain or snow when the ground below is soft and wet, excess weight in the container can compress the concrete on the ground and lead to cracking. Homeowners who live there who park their luxury cars or garbage dumps on their driveways often see this kind of cracking.
6. Concrete cracks are caused by premature drying
Cracks for premature drying
There are two common types of cracks caused by premature drying.
Cracking cracks are very good, more cracks like spider webs or cracked glass. When the surface of the concrete slide loses moisture very quickly, cracks may form. While unsightly, sector fragmentation is not a construction concern.
Splitting cracks occur during the concrete installation process, which is a way to add texture or pattern to concrete areas. On hot or windy days when the top of the slide dries faster than the bottom, the top of the concrete surface can bend. When the stamp is embedded, it pulls the surface farther away from the sealed joints and creates small cracks around the outer edges of the “stones”. And, although they may not look good, splitting spears is not a structural problem to consider.
It is often difficult to pinpoint exactly what caused an explosion. Proper site preparation, quality mixing, and good concrete finishing practices can go a long way in reducing the appearance of cracks and producing a more enjoyable concrete project.
We cannot stress the importance of quality design in concrete control. Read the Concrete Checklist: Find the Best Mix for Your Project, which will show you and your concrete provider how to create the right mix for your integration project.
VIBRATION