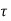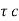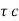Unit-2
Behavior of RC beam in Shear
Q1) Explain behavior of RC beam in shear
A1) Shear in Structural Members
Shear Stress in Homogenous Beams
The beam subjected to transfers is subjected to shear force and bending moment.
The shear stress induced in the member to resist shear force.
As per elastic theory of bending, shear stress distribution across the section is given by equation.
 = V (A y)/ I b
= V (A y)/ I b
Where,
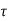 = Shear stress
= Shear stress
I = Moment of inertia of section
b = Width of the section
V = shear force at the section.
Shear stress induced in rectangular section is parabolic in nature with zero at top and bottom and the maximum shear stress at neutral axis.
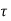 max = 3/2 V /b d
max = 3/2 V /b d
Shear Stresses in R.C.C. Beams
In reinforced concrete beam, the concrete below the neutral axis is neglected and shear force is resisted by the bound between the steel and concrete.
The shear stress in RC beam is parabolic with zero at top and maximum at neutral axis.
The shear stress below the neutral axis is constant in tensile zone.
Total shear force in the section V is given by
V = Area of stress diagram x breadth of the beam
= [Area of parabolic part + area of rectangular part] x breadth of the beam.
= [2/3 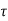 +
+ 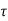 (d – x)] b
(d – x)] b
= [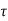 d -
d - 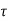 x/3] b
x/3] b
= 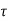 [d – x/3] b
[d – x/3] b
= 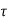 [d – k d/3] b
[d – k d/3] b
=  d [1 – k/3] b
d [1 – k/3] b
V = 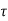 b j d
b j d
 = V / b j d
= V / b j d
Nominal Shear Stress
The shear stress occurs along with the flexural stress. The inclined cracking effects due to resultant tension are complex and concrete in tension also contributes in retesting shear up to some extent, hence the evaluation of shear stress is very complex.
In IS 456 : 2000, the equation of shear stress is simplified by replacing lever arm factor (j d) by the effective depth, the shear stress obtained is called as nominal shear stress
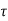 v = V /b d
v = V /b d
Where,
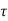 v = nominal shear stress
v = nominal shear stress
b = breadth of member
d = effective depth
Nominal shear stress in beams of varying depth
Beams of varying depth this case is formed then the nominal shear stress is calculated by
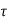 v = V +- M/d tan
v = V +- M/d tan 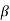 /b d
/b d
Where,
M = bending moment at the section
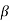 = Angle between the top and bottom edge of the beam
= Angle between the top and bottom edge of the beam
Negative sign is applied when moment M increases numerically in the same direction as effective depth increases and positive sign when M, decreases in this direction.
Cantilever beam, continuous beam with haunches at support are the common example of beans with varying depth.
Q2) What are the types of shear reinforcement
A2) Types of Shear Reinforcement
Vertical stirrups
Inclined stirrups
Bent up bars
This types are explain as follows,
Vertical stirrups
Steel bars vertically placed around the tensile reinforcement at suitable spacing along the span of beam to prevent diagonal cracks.
Diameter of stirrups varies from 6 mm to 16 mm.
The free end of stirrup is tree in compression zone only.
Inclined stirrups
Inclined stirrups are provided to resists diagonal tension. Inclination of stirrup are provided 45°.
Bent up bars
The longitudinal bars are bent up near the support to resist diagonal tension.
Bars are bent-up near the support where bending moment is very less.
Equal numbers of bars are bent up to maintain symmetry.
Shear resistance by bent up bars is not greater than half of the total shear reinforcement.
Form of Vertical Stirrups
Depending upon the magnitude of shear force the vertical stirrups used in any form as given
Single legged stirrup
Two legged stirrup
Four legged stirrup
Six legged stirrup
Q3) How to design shear reinforcement
A3) Design of shear reinforcement
When shear force Vu (or shear stress 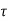 v) at a section is less than the shear resistance of concrete V (or design shear stress in concrete
v) at a section is less than the shear resistance of concrete V (or design shear stress in concrete 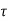 c), No shear reinforcement is required.
c), No shear reinforcement is required.
 v <
v <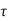 c, No shear reinforcement required
c, No shear reinforcement required
When nominal shear stress 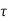 v is greater than design shear stress, shear reinforcement is required to prevent formation of cracks
v is greater than design shear stress, shear reinforcement is required to prevent formation of cracks
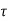 v >
v >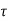 c, shear reinforcement is required.
c, shear reinforcement is required.
When nominal shear stress  v, greater than maximum shear stress in concrete, the section is not suitable so redesign of section.
v, greater than maximum shear stress in concrete, the section is not suitable so redesign of section.
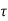 v >
v >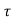 c max Redesign the section
c max Redesign the section
Shear strength of section
Vu = (shear capacity of concrete) + (shear resistance by stirrups) + (shear resistance by bent up bars)
= V u c + V a s + V u s b
Shear capacity of concrete
V u c = 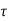 c b d
c b d
For vertical stirrups
V u s =
For inclined stirrups or series of bars bent up at different section.
V u s = (Sin 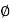 + Cos
+ Cos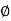 )
)
For single bent up or all bent up bar at same level
V u s = 0.87 f y A s v sin 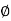
Where,
A s v = Area of stirrups legs effective in shear
S v = Spacing of stirrups
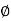 = Angle between inclined stirrups or bent-up bar, not less than 45°
= Angle between inclined stirrups or bent-up bar, not less than 45°
d = effective depth
f y= characteristic strength of stirrup reinforcement which shall not be greater than 415 N/mm2
Spacing of stirrup should be minimum of following conditions
S v should not be greater than 0.75 d
S v should not be greater than 300 mm
Q4) 1) A reinforced concrete rectangular beam has width 230 mm and total depth 600 mm with clear cover of 25 mm. The beam is reinforced with 3 bars with 16 mm diameter at support section at tension side. Calculate shear strength of the support section if 8 mm diameter two legged stirrups are provided at spacing 150 mm c/c. Use M20 grade of concrete and Fe415 grade of steel. Use LSM.
A4)
Given:
b = 230 mm
D = 600 mm
Clear cover = 25 mm
A s t = 3-16 mm diameter
A s v = 8 mm diameter 2 legged stirrups.
To find: Shear resistance Vu
Solution:
Area of steel tension A s t = n • d2 = 3 • 162 = 603.2 mm2
Area of vertical stirrups A s v = n • d2 = 2 • 82 = 100.5 mm2
Spacing of stirrups S v = 150 mm
Effective depth d = D – c – d/2
= 600 – 25 – 16/2
= 567 mm
Step 1: Design shear strength in concrete ( c) :
c) :
% pt = 0.46
Refer table 19, page no 73 of IS 456 – 2000
For M20 and = 0.46, 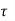 c by interpolation
c by interpolation
|
|
0.25 | 0.36 |
0.5 | 0.48 |
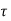 c = 0.36 + (0.46 – 0.25)
c = 0.36 + (0.46 – 0.25)
= 0.462 N/mm2
Step 2: Shear capacity of concrete ( Vu c)
V u c =  b d
b d
= 0.462 x 230 x 567
= 60250 N
= 60.25 KN
Step 3: Shear resistance by vertical stirrups:
V u s =
= 137160 N
= 137.16 KN
Step 4: Total shear capacity of RC beam:
Vu = V u c + V u s
= 60.25 + 137.16
= 197.41 KN
Q5) Determine the shear capacity of RC beam 300 x 550 mm effective reinforced with 4 bars tension reinforcement and 8 mm diameter two legged stirrups @ 150 mm c/c throughout the beam, if (1) no bent up bars are provided and (2) 2 bars are bent up. Use M20 and Fe415 grade materials.
A5)
Given
b = 300 mm
d = 550 mm
A s t = 4 – 25 mm diameter of bar
Stirrups - 2 legged 8 mm diameter of bar @ 150 mm c/c
To find: Shear capacity Vu
Solution:
Area of steel tension A s t = n • d2 = 4 • 252 = 1963.5 mm2
Area of stirrups A s v = n • d2 = 2 • 82 = 100.5 mm2
Spacing of stirrups S v = 150 mm
Case 1: No bent up bar are provided
Step 1: Design shear strength in concrete ( c ) :
c ) :
% pt = 1.196 = 1.2
Refer table 19, page no 73 of IS 456 – 2000
For M20 and = 1.2, 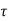 c by interpolation
c by interpolation
|
|
1 | 0.62 |
1.25 | 0.67 |
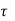 c = 0.62 + (1.2 – 1.0)
c = 0.62 + (1.2 – 1.0)
= 0.66 N/mm2
Step 2: Shear capacity of concrete (V u c)
V u c = 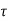 b d
b d
= 0.66 x 300 x 550
= 108900 N
= 108.9 KN
Step 3: Shear resistance by vertical stirrups:
V u s =
= 133.05 x 103 N
= 133.05 KN
Step 4: Total shear capacity of RC beam:
Vu = V u c + V u s
= 108.9 + 133.05
= 241.95 KN
Case 2: Two bent up bar are provided
Step 1: Design shear strength in concrete (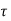 c):
c):
A s t at support is only for 2 bars out of 4 bars, because 2 bars are bent up,
Area of steel tension A s t = n • d2 = 2 • 252 = 981.75 mm2
% pt = 0.595 = 0.6
Refer table 19, page no 73 of IS 456 – 2000
For M20 and = 0.6, 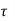 c by interpolation
c by interpolation
|
|
0.5 | 0.48 |
0.75 | 0.56 |
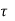 c = 0.48 + (0.6 – 0.5)
c = 0.48 + (0.6 – 0.5)
= 0.512 N/mm2
Step 2: Shear capacity of concrete (V u c)
V u c = 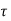 b d
b d
= 0.512 x 300 x 550
= 84480 N
= 84.48 KN
Step 3: Shear resistance by vertical stirrups:
V u s =
= 133.05 x 103 N
= 133.05 KN
Step 4: Shear resistance by bent up bars:
V u s v = 0.87 f y A s v sin
= 0.87 x 415 x (2 • 252) x sin 45°
= 250640 N
= 250.64 KN
Step 5: Total shear capacity of RC beam:
Vu = V u c + V u s+ V u s v
= 84.48 + 133.05 + 250.64
= 468.17 KN
Q6) Explain minimum and maximum shear reinforcement
A6) MINIMUM AND MAXIMUM SHEAR REINFORCEMENT
Maximum Shear Stress
The nominal shear stress (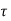 v) in the beam with shear reinforcement shall not exceed maximum shear stress (
v) in the beam with shear reinforcement shall not exceed maximum shear stress (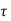 c max)
c max)
Maximum shear stress in concrete is given in Table 20, page no, 72 of IS 456: 2000
Concrete Grade | M15 | M20 | M25 | M30 | M35 | M40 And above |
| 2.5 | 2.8 | 3,1 | 3.5 | 3.7 | 4.0 |
If nominal shear stress is greater than the maximum shear stress (𝜏r >𝜏c ma ) the section is to be redesign.
Minimum Shear Reinforcement
When the nominal shear stress 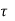 r is less than the design shear strength of concrete (
r is less than the design shear strength of concrete (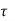 c), then no shear reinforcement is to be required.
c), then no shear reinforcement is to be required.
In such cases, minimum shear reinforcement is to be provided in the form of stirrups.
A s v / b. S v = 0.4 /0.87 f y
Where,
A s v = Total area of stirrup legs effective in shear.
S v = Spacing of stirrups along the length of members
b = breadth of member
F y = Characteristic compressive strength of the stirrup reinforcement which shall not be greater than 415 mm2
Necessity of Minimum Shear Reinforcement
To prevent failure due to shrinkage, thermal stresses and internal cracking in the beam .
Maximum Spacing of Shear Reinforcement
As per IS456: 2000, clause 26.5.1.5, page No. 47, the maximum shear reinforcement measured along the axis of member shall be as below:
Stirrups | Spacing (whichever is less ) |
Vertical stirrups | 0.75 d or 300 mm |
Inclined stirrups | D or 300 mm |
Where, d = effective depth of section.
Q7) Explain development length and anchorage bond
A7)
Development length
Development length is the minimum length required to provide a perfect bond between steel and concrete, so that steel will not slip from harden concrete.
It is denoted by L d
Tensile force in bar = d2 x f s
Bond force = 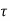 b d (d L d)
b d (d L d)
Equating bond force to tensile force
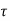 b d (d L d) = d2 x fs
b d (d L d) = d2 x fs
But f s = 0.87 f y
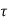 b d x L d = x 0.87 fy
b d x L d = x 0.87 fy
L d =
Where, d = diameter of bar
This is applicable for mild steel.
For HYSD, bond stress is increased by 60%
L d =
Anchorage bond
Bars in Tension (cl. 26.2.2.1 of IS456)
Bends and hooks shall conform to IS 2502.
1) Bends
Bends, conforming to standards are frequently resorted to in order to provide anchorage, contributing to the requirements of development length of bars in tension or compression.
The Code (Clause 26.2.2.1 b(1)) specifies that "the anchorage value of a bend shall be taken as 4 times the diameter of the bar for each 45° bend, subject to a maximum of 16 times the diameter of the bar".
Commonly a 'standard 90° bend' (anchorage value = 8 x diameter of bar) is adopted, including a minimum extension of 4.
2) Hooks
When the bend is turned around 180° (anchorage value = 16 x diameter of bar) and extended beyond by 4 x diameter of bar, it is called a standard U-type hook.
The minimum (internal) turning radius specified for a hook is 2 x diameter of bar for plain mild steel bars and 4 x diameter of bar for cold-worked deformed bars. Hooks are generally considered mandatory for plain bars in tension (Clause 26.2.2.1a of IS456: 2000].
In the case of stirrup (and transverse tie) reinforcement, the Code (Clause 26.2.2.4b) specifies that complete anchorage shall be deemed to have been provided if any of the following specifications is satisfied:
90° bend around a bar of diameter not less than the stirrup diameter, with an extension of at least 8 x diameter of bar
135° bend with an extension of at least 6 x diameter of bar
180° bend with an extension of at least 4 x diameter of bar
Q8) Explain flexural bond and failure of beam under shear
A8)
FLEXURAL BOND
The RCC bond is the adhesive force which is developed between concrete and reinforcing steel to transfer the axial force from a reinforcing bar to the surrounded concrete.
Bond ensures the strain compatibility of RCC.
Bond between steel and concrete can be improved due to
1) Use of rich mix
2) Perfect compaction and curing
3) Adequate cover to steel
4) Use deformed bar
Bond Stresses
The shear stress developed along the contact surface of the reinforced bar and concrete is defined as bond stress.
It is denoted by 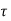 b d
b d
The main function of bond stress to prevent slipping of bar through the harden concrete.
The value of bond stress for bars in tension by clause 26.2.1.1, page no 43 of IS456: 2000 is as given in table.
Type of steel | M20 | M25 | M30 | M35 | M40 and above |
Mild steel Fe 250 | 1.2 | 1.4 | 1.5 | 1.7 | 1.9 |
Mild steel Fe 415 and Fe 500 | 1.92 | 2.24 | 2.4 | 2.72 | 3.04 |
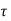 b d for bar in compression, the value of
b d for bar in compression, the value of 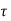 bd is increased by 25%.
bd is increased by 25%.
FAILURE OF BEAM UNDER SHEAR
When the shear pressure on an object exceeds the maximum allowable shear pressure, then the object has a failure known as shear failure. Shear failure can be defined as a failure that occurs due to insufficient stock resistance found between building materials.
Shear force is the force of an object or object that is opposed to the type of yield or structural failure where the instrument or part fails in the stock.
A shear load is a force that often produces a slippery slope in an object in a plane that is aligned with the direction of force.
In simple terms, the shear pressure is greater at 45 ° in the cross section of the beam so diagonal formation is formed at shear failure and shear failure occurs at the end of the beam where the beam connects to the column. To avoid this type of seizure failure is provided.
Shear failure can be easily detected by examining excessive deviations or crevices, which gives advance warning of possible shear failure.
It is difficult to comprehend the extent to which reinforcement and concrete will work, and predict the exact timing of shear failure.
Reasons for penind failure is failure there is
Q9) A rectangular R.C.C. beam 300 x 700 mm with effective cover 40 mm is subjected to following actions.
Factored B.M. = 190 k N-m
Factored S.F. 50 k N
Factored Torsion moment = 20 k N-m
Design the beam for flexure and shear using M20 and Fe 415.
A9)
Given:
Breadth b = 300 mm,
Overall depth D= 700 mm
Effective cover C = 40 mm,
Factored B.M. Mu = 190 k N-m
Factored S.F. Vu = 50 k N-m,
Factored Torsion T u = 20 k N-m
F c k = 20 N/mm2
F y = 415 N/mm2
To find: Reinforcement
Solution:
Effective depth d = D – c = 700 – 40 = 600 mm
Mt = T u (1 + D/b)/1.7
= 20 (1 + 700/300)/ 1.7
= 39.22 K Nm
Mu > M t, only tension reinforcement designed there is no need of compression reinforcement due to twisting moment.
Equivalent moment,
Me = Mu + Mt
= 190 +39.22
= 229.22 K Nm
Limiting moment of resistance for Fe415
Mu limiting = 0.138 f c k bd2
= 0.138 x 20 x 300 x 6602
= 30.7 x 106 N.mm = 360.7 K Nm
Since Mu e< Mu limiting, the section is designed as singly reinforced beam.
Area of tensile steel,
A s t = 0.5 f c k /f y (1 -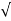 1 – ((4.6 M u)/ (f c k b d2) b d
1 – ((4.6 M u)/ (f c k b d2) b d
A s t = 1085.9 mm2
Number of bars (Assume 20 mm diameter of bar)
n =A s t/A d =1085.9/314.2 = 3.5 = 4 bars
A s t provided = n • d2 = 4 • 202 = 1256.6 mm2
Percentage of steel:
% pt = 100 A s t/b d = 100 * 1256.6/300 * 660 = 0.635 %
Provided 4 – 20 mm diameter of bar as tensile steel
Equivalent shear
V u e = Vu + 1.6 T u /b
= 50 + 1.6 (20/0.3)
= 50 + 106.67
= 156.67 K Nm
b1 = Centre to centre distance between corner bars in the direction of width of beam
= b – 2 x side cover – diameter of main bar
= 300 – 2 x 25 – 20 = 230 mm
d1 = Centre to centre distance between corner bars in the direction of depth of beam
= 600 – (2 x 25) – 20/2 – 12/2
= 594mm
Equivalent shear stress
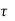 v c =V u e/b d = 156.67 * 103 /300 * 660 = 0.79 N/mm2
v c =V u e/b d = 156.67 * 103 /300 * 660 = 0.79 N/mm2
Design shear strength of concrete
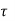 c for M20 and %pt = 0.635 %
c for M20 and %pt = 0.635 %
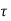 c = 0.48 + (0.635 – 0.5)
c = 0.48 + (0.635 – 0.5)
= 0.523 N/mm2
For M20, 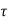 c max = 2.8 N/mm2
c max = 2.8 N/mm2
Since, 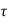 v >
v >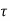 c <
c <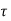 c max, transverse reinforcement is to be design for torsion
c max, transverse reinforcement is to be design for torsion
Shear capacity of concrete (V u c)
V u c = 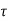 b d
b d
= 0.523 x 300 x 660
= 103.6 x 106 N
= 103.6 KN
Shear capacity of steel reinforcement:
V u s = V u e – V u c
= 156.67 – 103.6
= 53.07 KN
Use 6 mm diameter of bar – 2 legged vertical stirrups
A s t = n • d2 = 2 • 62 = 56.54 mm2
S v = 0.87 f y * b1 d1 As v /T u + 0.87 f y * 2.5 d1 /V u
= 139 mm = 130 mm c/c
Provided 6 mm diameter – 2 legged vertical stirrups @ 130 mm c/c
Q10) A rectangular RC beam of span 6 m, size 300 mm x 600 mm with effective cover 40 mm is subjected to following actions:
(a) Factored BM = 90 k Nm
(b) Factored SF = 60 k N
(c) Factored Torsion moment = 35 k Nm
Design the beam for the flexure and shear using M 25 and Fe 500 grade materials
A10)
Given:
Span L= 6 m,
Ceffective = 40 mm
Width b = 300 mm,
Depth D = 600 mm,
Vu = 60 k N M
F c k = 25 N/mm2
F y = 500 N/mm2
Mu = 90 KN. M
T u = 35 KN. M
To find: A s t , A s v
Solution:
Effective depth d = D – c = 600 – 40 = 560 mm
Step 1: Equivalent bending moment:
Mt = T u ((1 +D/b)/1.7)
= 35 (1 +600/300)/1.7)
=61.76 K Nm
Mu > M t , longitudinal reinforcement shall be provided on flexural steel side.
Equivalent moment,
Me = Mu + Mt
= 90 +61.76
=151.7 K Nm
Step 2: Check for required of depth for flexure with torsion
Limiting moment of resistance for Fe500
Mu limiting = 0.133 f c k bd2
151.7 x 106 = 0.133 x 25 x 300 x d2
= 393 mm < 560 mm ………OK
Step 3: Longitudinal reinforcement
Area of tensile steel,
A s t = 0.5 f c k /f y (1 -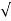 1 – ((4.6 M u)/ (f c k b d2) b d
1 – ((4.6 M u)/ (f c k b d2) b d
A s t = 678 mm2
Number of bars (Assume 16 mm diameter of bar)
n =A s t/A d = 678/201 = 3.4= 4 bars
A s t provided = n • d2 = 4 •162 = 804 mm2Hanger bars
Provided 2 – 12 mm diameter hanger bars.
Step 4: Design for shear reinforcement:
Equivalent shear
V u e = Vu + 1.6
= 60 + 1.6
=246.67 K Nm
Shear capacity of concrete V u s
% pt = 100 A s t/b d = 100 * 804 /300 * 560 = 0.478 % = 0.5 %
Shear stress in concrete ( c )
c )
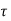 c for M25 and %pt = 0.7 %
c for M25 and %pt = 0.7 %
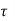 c = 0.49 N/mm2 ( % pt = 0.5 % )
c = 0.49 N/mm2 ( % pt = 0.5 % )
V u c = 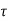 b d
b d
= 0.49 x 300 x 560
= 82.32 x 106 N
= 82.32 KN
V u e> V u c (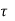 u e >
u e >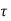 c) shear reinforcement is required.
c) shear reinforcement is required.
Assume side cover 25 mm and effective cover for top and bottom reinforcement is 40 mm c/c distance corner bars in direction of width of beam
b1 = Centre to centre distance between corner bars in the direction of width of beam
= b – 2 x side cover – diameter of main bar
= 300 – 2 x 25 – 20 = 230 mm
d1 = Centre to centre distance between corner bars in the direction of depth of beam
= 600 – (2 x 20) – 40
= 520 mm
Use 8 mm diameter of bar – 2 legged vertical stirrups
A s v = n • d2 = 2 • 82 = 100.53 mm2
S v = 0.87 f y * b1 d1 A s v /T u + 0.87 f y * 2.5 d1 /V u
= 128.4 mm = 125 mm c/c
S v = 0.87 F y * A s v d/ (V u e – V c e)
= 149 mm
Maximum spacing on shorter span:
Spacing for 8 mm diameter of bar 2 – legged stirrups @ 125 mm
Step 5: Additional longitudinal bars:
When cross sectional dimension of member exceeds 450 mm, additional longitudinal bars shall be provided to satisfy the requirements of minimum side face reinforcement and spacing.
Effective depth d = 600 mm > 450 mm
Side face reinforcement as per Is 456 – 2000
= 0.1 % (web area)
= 0.1 /100 x 300 x 600 = 180 mm2
Number of side reinforcement of 8 mm diameter
n = A s t/A d = 3.62 = 4 bars.