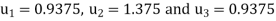Unit-5

Boundary value problems

Q1) Solve the boundary value problem defined by

by finite difference method. Compare the solution at y (0.5) by taking h=0.5 and h=0.25.

A1) Given equation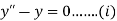

With boundary   condition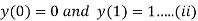   

By finite difference method

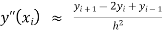       …. (iii)

Putting(iii) in (i) we get

       …. (iv)

For h=0.5, here for 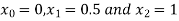which corresponds to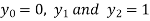

For i=1 in equation (iv) we get

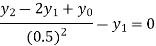
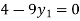
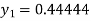
For h=0.25, here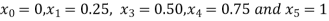

Which corresponds to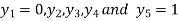 

For i=1 in equation (iv) we get

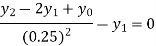
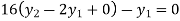
For i=2 in equation (iv) we get

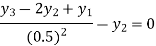
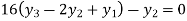
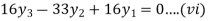
For i=3 in equation (iv) we get

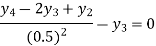
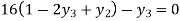
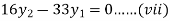
From   equation (v), (vi) and (vii) we get

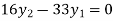
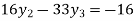
On solving above triangular   equation we get

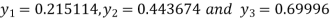
Hence for h=0.5 we   get    y (0.5) =0.44444

And for h=0.25 we get y (0.5) =0.443674

Q2) Solve the bounded value problem

With boundary condition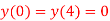 

A2) Given equation

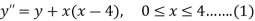
With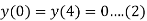 

By finite difference method

       …. (3)

Putting (3) in equation (1) we have

By finite difference method

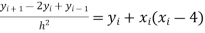…… (4)

Let h=1, we have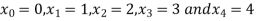

Corresponds to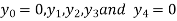 

For i=1 in equation (4) we get

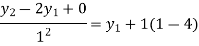
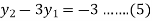
For i=2 in equation (4) we get

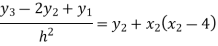
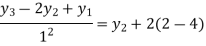
For i=3 in equation (4) we get

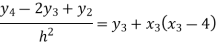
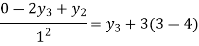
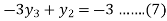
From equation (5), (6) and (7) we get

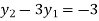
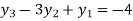
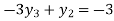
On solving we get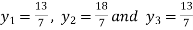

Q3) Solve the boundary value problem

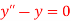
With y (0) =0 and y (2) =3.62686

A3) Given equation 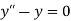  …. (1)

With boundary condition y (0) =0 and y (2) =3.62686…. (2)

   By finite difference method

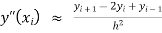       …. (3)

Substituting (3) in equation (1) we get

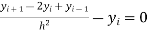…. (3)

Let h=0.5 then for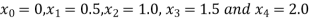 

Which corresponds   to 

For   i=1 in equation (3) we get

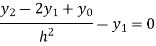
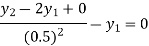
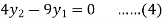
    For   i=2 in equation (3) we get

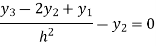
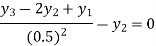
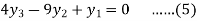
    For   i=3 in equation (3) we get

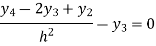
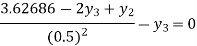
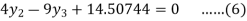
 From equation (4), (5) and (6) we get

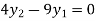
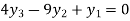
On solving we get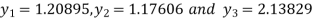 

Q4) Explain how do we find the smallest Eigen value.

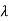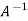A4) If is the Eigen value of A, then the reciprocal is the Eigen value of , then the reciprocal of the largest Eigen value of 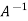will be the smallest Eigen value of A.

Q5) Explain power method.

A5) Procedure for Power method-

Step-1: First we choose an arbitrary real vector 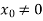, basically 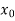is chosen as-

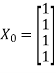
Step-2: Compute 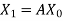, , 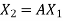, , 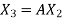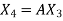………… 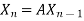Put

Step-3: compute , ,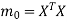

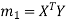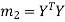
Step-4: The largest Eigen value is

The error in can be find as-

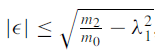
The Eigen vector corresponding to 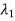is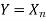

Q6) Find the largest Eigen value and the corresponding Eigen vector of the matrix

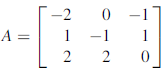
Also find the error in the value of the largest Eigen value.

A6)

Let us choose the initial vector

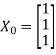
Then

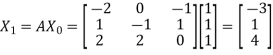
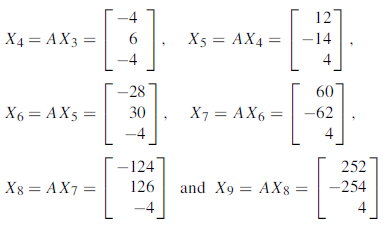
Now put 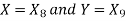, then-

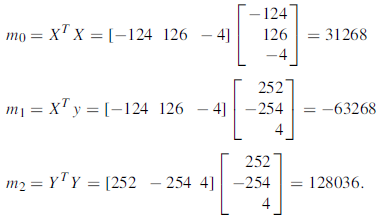
Hence the largest Eigen value is-

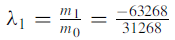
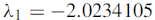
And the corresponding Eigen vector is-

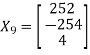
The error can be calculated as-

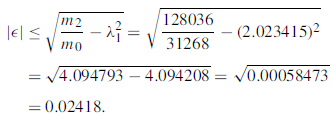
Q7) Give the classification of PDE’s.

A7) The general linear PDE of the second order in two independent variables is of the form-

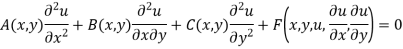
Then there are three conditions-

If

If

If

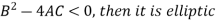
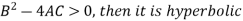
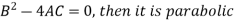
Q8) Classify the equation-

A8) Here A =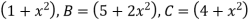

Now

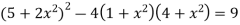
That means,

The equation is hyperbolic.

Q9) Classify the equation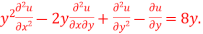

A9) Here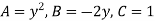

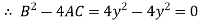
Hence the equation is parabolic

Q10) Solve the Laplace’s equation  in the domain

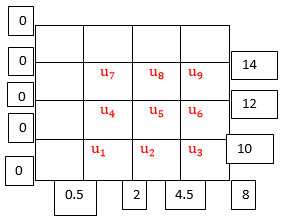
A10) The initial values using five diagonal formula we have

Here ,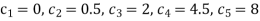 

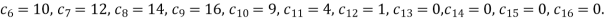
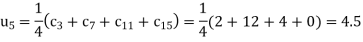
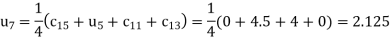
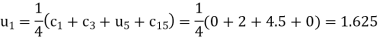
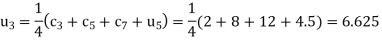
The remaining quantities are calculated by using standard five-point diagonal formulas.

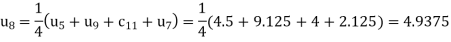
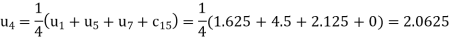
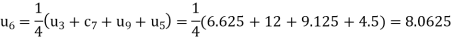
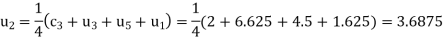
Hence 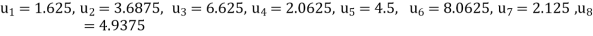and .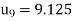

Q11) Solve the Laplace’s equation for

A11) The initial values using five diagonal formula we have

Here ,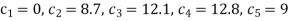 

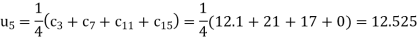
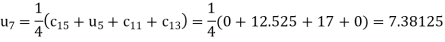
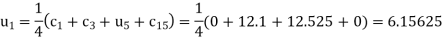
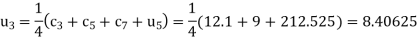
The remaining quantities are calculated by using standard five-point diagonal formulas.

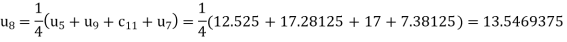
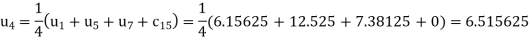
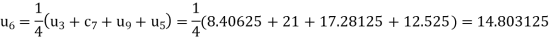
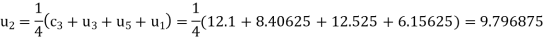
Hence 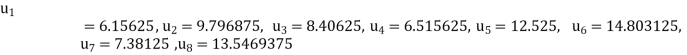and .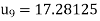

Q12) Solve the elliptical equation for

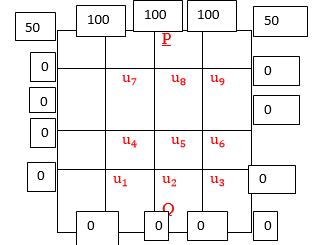
A12) The initial values using five diagonal formula we have

Here , 

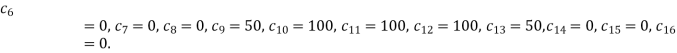
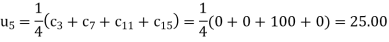
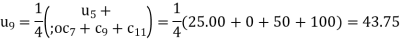
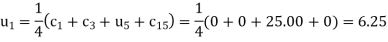
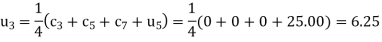
The remaining quantities are calculated by using standard five-point diagonal formulas.

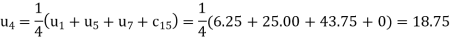
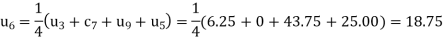
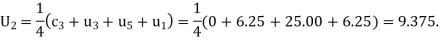
The Above is symmetric about PQ, so that .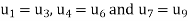

We will have iteration process using the Gauss Seidal Formula

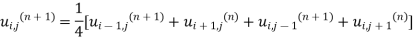
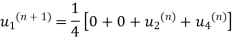
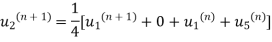
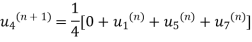
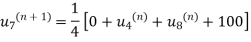
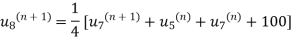
First iteration: Putting 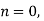we get

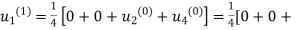
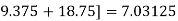
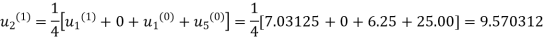
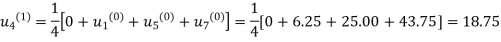
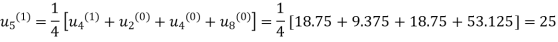
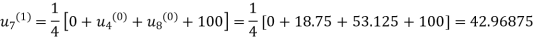
Second Iteration: Putting 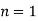, we get

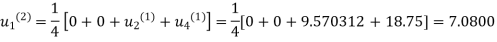
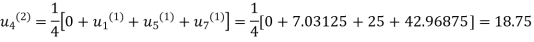
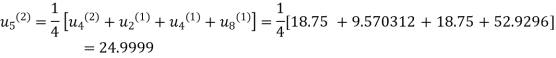
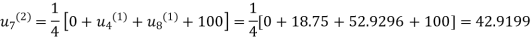
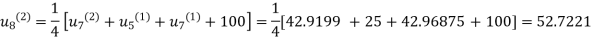
Third Iteration: Putting 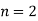, we get

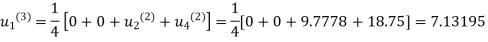
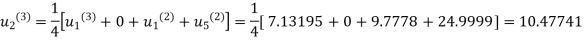
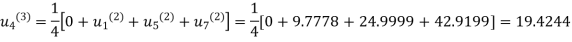
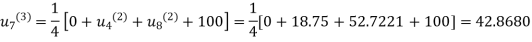
Fourth Iteration: Putting 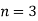, we get

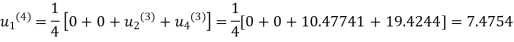
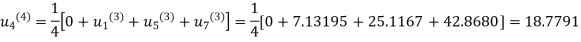
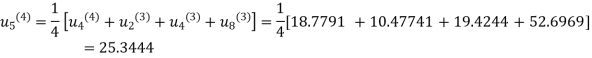
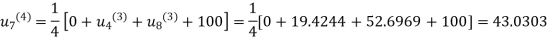
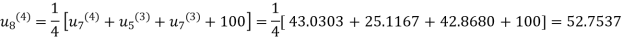
   Fifth iteration: Putting n=4 we get

.

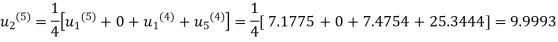
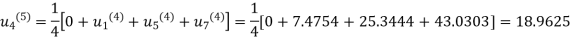
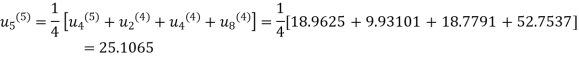
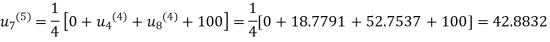
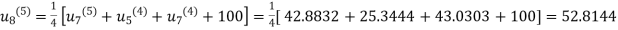Q13) Solve the Poisson equation

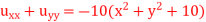
A13) Let the point be defined by At the point A, . The standard five-point formula at point A is

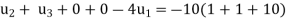
Or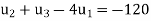  

Or 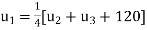      ….(i)

Again, the standard five-point formula at the point B is

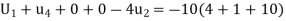
Or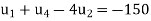 

Or 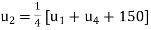  ….(ii)

Similarly, the standard five-point formula at the point C

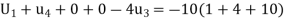
Or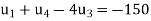

Or 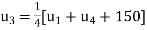    …. (iii)

Similarly, the standard five-point formula at the point D

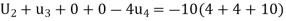
Or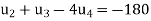

Or 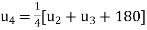     …. (iv)

From (ii) and (iii) we get 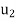=. Hence the iteration formula we have

.

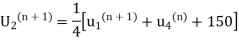
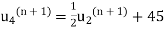First iteration: Putting 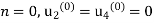. Hence, we obtain

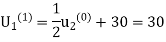
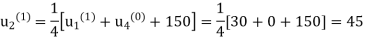
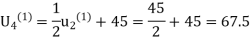
Second iteration: Putting n=1, we get

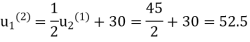
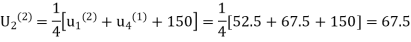
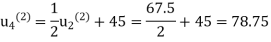
Third iteration: Putting n=2, we get

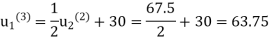
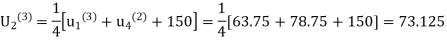
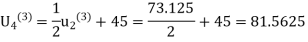
Fourth iteration: Putting n=3, we get

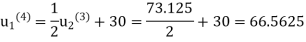
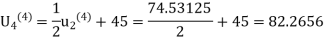
  Fifth iteration: Putting n=4, we get

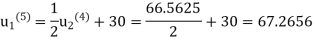
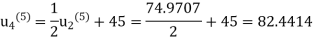
Sixth iteration: Putting n=5, we get

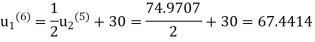
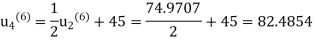
Since last two iteration are approximately equal, hence

.

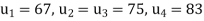Q14) Solve the equation 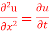with the conditions . Assume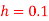. Tabulate u for 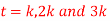choosing appropriate value of k?

A14) Here and let   ,

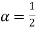Since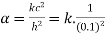

The Bendre-Schmidt recurrence formula we have

  …. (i)

Also given .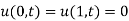

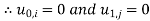for all values of j, i.e., the entries in the first and the last columns are zero.

Since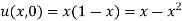

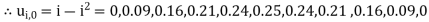  (Using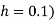

For .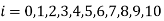

Putting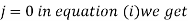

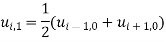
Putting 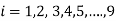successively we get

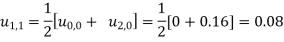
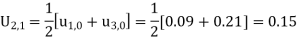
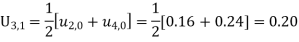
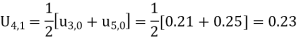
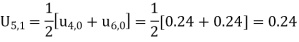
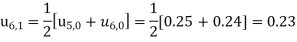
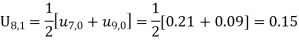
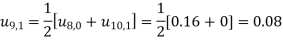
These will give the entries in the second row.

Putting in equation (i), we will get the entries of the third row.

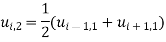
Similarly, 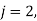successively in (i), the entries of the fourth rows are

obtained.

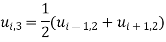
Hence the values of 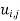 are as given in the below the table:

Q15) Solve the heat equation

Subject to the conditions 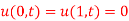and

.

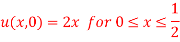
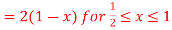A15) Take 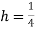and k according to Bendre-Schmidt equation.

Here 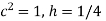and let   ,

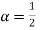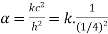
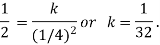
Since

The Bendre-Schmidt recurrence formula we have

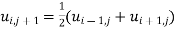  …. (i)

Also given .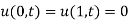

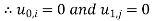for all values of j, i.e., the entries in the first and the last columns are zero.

Since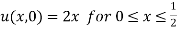  

.

.

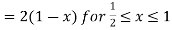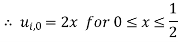
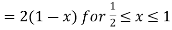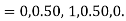
For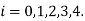  

Putting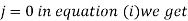

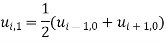
Putting successively we get

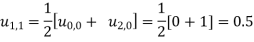
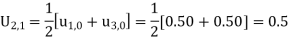
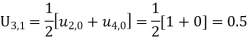
 These will give the entries in the second row.

Putting 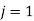in equation (i), we will get the entries of the third row.

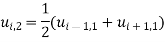
Similarly, 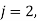successively in (i), the entries of the fourth rows are

obtained.

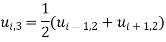
Hence the values of 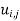 are as given in the below the table:

Q16) Use the Bendre-Schmidt formula to solve the heat conduction problem

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   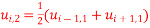With the condition 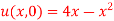and .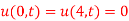

A16) Let 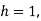we see when .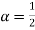

The initial condition is .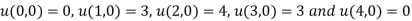

Also .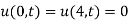

The iteration formula is

=

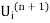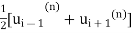
  First iteration: Putting n=0, we get

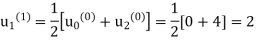
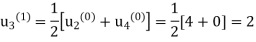
 Second iteration: Putting n=1, we get

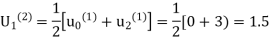
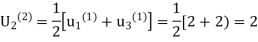
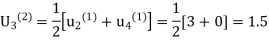
Third Iteration: putting n=3, we get

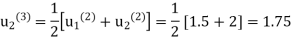
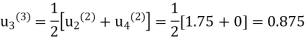
Fourth Iteration: putting n=3, we get

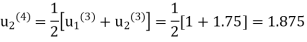
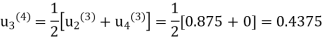
Fifth Iteration: putting n=4, we get

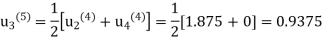
Hence the approximate solution is