Unit-1

Error and roots of Algebraic and Transcendental Equations

Q1) Describe some commonly used symbols in flow chart.

A1)

The commonly used symbols in a flow chart-

1.Terminal point

2. Input / Output-

3. Decision logic-

4. Processing operation box-

5. Connector point-

Q2) Define mean value theorem for derivatives.

A2) Mean value theorem for derivatives-

Suppose that f(x) be a function of x such that,

1. if it is continuous in [a, b]

2. if it is differentiable in (a, b)

Then there at least exists a value cϵ (a, b)

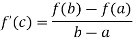
Q3) What do you understand by truncation error.

A3) The truncation errors are caused by approximated values or on replacing the infinite process to a finite value.

Example: 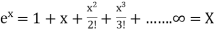is replaced by .

Then truncation error is

Q4) An approximate value of   is given by and its exact value is Find the absolute and relative errors.

A4) The absolute error is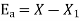

.

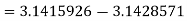
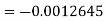The relative error is

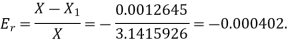
Q5) Find the difference   to three significant figures?

A5)

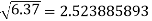
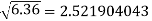
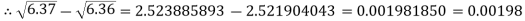
Correct to three decimal places.

Q6) Find the absolute error if the number is truncate to three decimal places?

A6) The given number is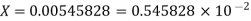

After truncate it to three decimal places the rounded value is

Therefore, the absolute error is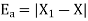

=

.

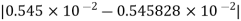
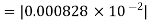
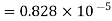Q7) Find a real root of 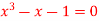using bisection method correct to five decimal places.

A7) Let 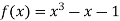then by hit and trial we have

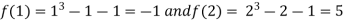
Thus 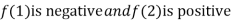.So the root of the given equation should lie between 1 and 2.

Now,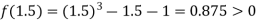

I.e., positive so the root of the given equation must lie between

Now,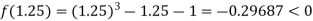

I.e., negative so the root of the given equation lies between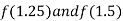

Now,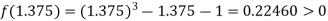

i.e., positive so the root of the given equation lies between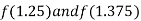

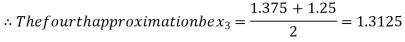
Now,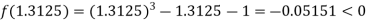

i.e., negative so that the root of the given equation lies between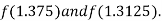

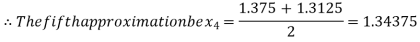
Now,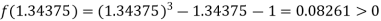

i.e., positive so that the root of the given equation lies between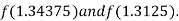

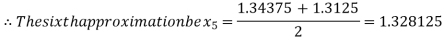
Now,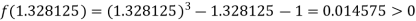

i.e., positive so that the root of the given equation lies between

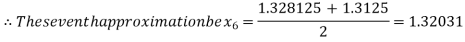
Now,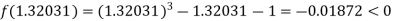

I.e., negative so that the root of the given equation lies between

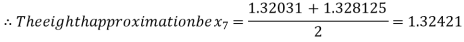
Now,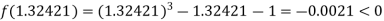

i.e., negative so that the root of the given equation lies between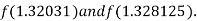

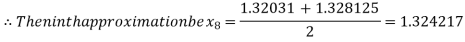
Hence the approximate root of the given equation is 1.32421

Q8) Find the root of the equation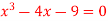, using the bisection method.

A8)  Let 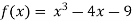then by hit and trial we have

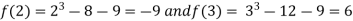
Thus 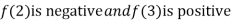.So the root of the given equation should lie between 2 and 3.

Now,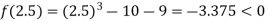

i.e., negative so the root of the given equation must lie between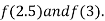

Now,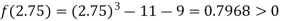

i.e., positive so the root of the given equation must lie between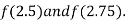

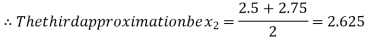
Now,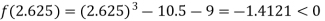

i.e., negative so the root of the given equation must lie between

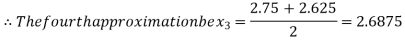
Now,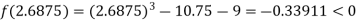

i.e., negative so the root of the given equation must lie between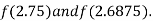

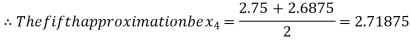
Now,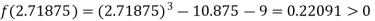

i.e., positive so the root of the given equation must lie between

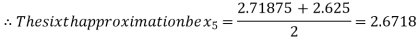
Now,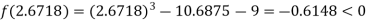

i.e., negative so the root of the given equation must lie between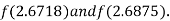

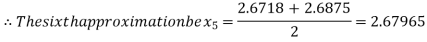
Hence the root of the given equation correct to two decimal place is 2.67965.

Q9) Find the root of the equation 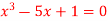  between 2 and 3, using bisection method correct to two decimal places.

A9) Let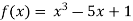

Where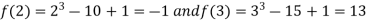

Thus 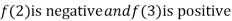.So the root of the given equation should lie between 2 and 3.

Now,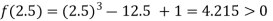

i.e., positive so the root of the given equation must lie between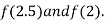

Now,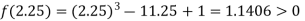

i.e., positive so the root of the given equation must lie between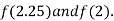

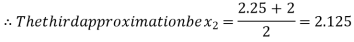
Now,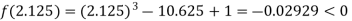

i.e., negative so the root of the given equation must lie between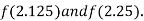

Now,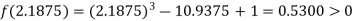

i.e., positive so the root of the given equation must lie between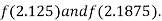

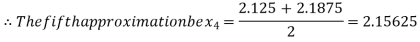
Now,

i.e., positive so the root of the given equation must lie between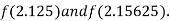

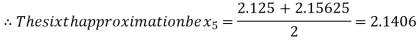
Now,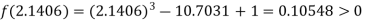

i.e., positive so the root of the given equation must lie between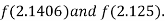

Now,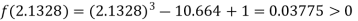

i.e., positive so the root of the given equation must lie between

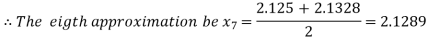
Now,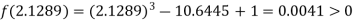

i.e., positive so the root of the given equation must lie between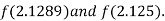

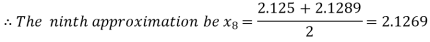
Hence the root of the given equation correct to two decimal place is 2.1269

Q10) Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.

A10) Here we have-

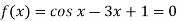
Now,

A root lies between 0 and .

We can rewrite the equation as-

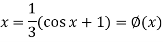
We have-

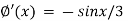
And

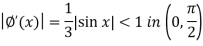
Here we can apply iteration method, starting with

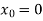
Then the successive approximation is-

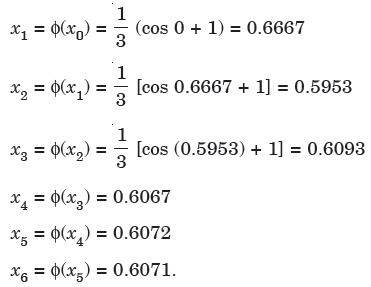
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.

Q11) Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.

A11) Here

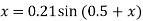
First approximation of x is gives as-

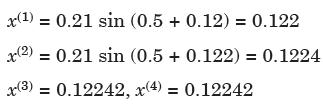
Here last two approx. are same, hence required root is 0.12242.

Q12) Define the method of false position (Regula- Falsi method)

A12) This is the oldest method of finding the approximate numerical value of a real root of an equation.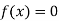

In this method we suppose that and 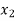are two points where 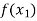and 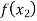are of opposite sign. Let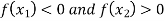

Hence the root of the equation 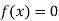lies between 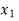and 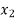and so,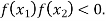

The Regula Falsi formula

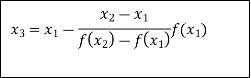
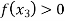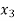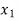Find is positive or negative. If then root lies between and or if 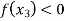then root lies between 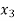and 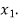 similarly we calculate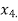

Proceed in this manner until the desired accurate root is found.

Q13) Find a real root of the equation near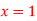, correct to three decimal places by the Regula Falsi method.

A13) Let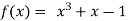

 Now,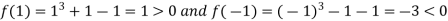

And also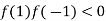

Hence the root of the equation 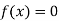lies between 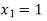and and so,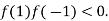

By Regula   Falsi Method

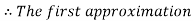
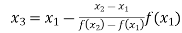
Now,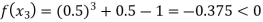

So, the root of the equation 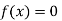lies between 1 and 0.5 and so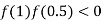

By Regula Fasli Method

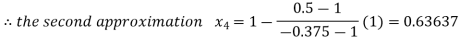
Now,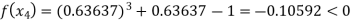

So, the root of the equation 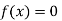lies between 1 and 0.63637 and so

By Regula Fasli Method

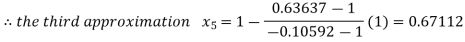
Now,

So, the root of the equation 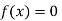lies between 1 and 0.67112 and so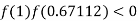

By Regula Fasli Method

Now,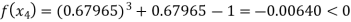

So, the root of the equation 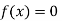lies between 1 and 0.63636 and so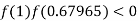

By Regula Fasli Method

Now,

So, the root of the equation 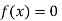lies between 1 and 0.68168 and so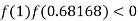

 By Regula Fasli Method

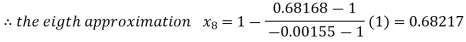
Now,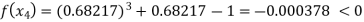

Hence the approximate root of the given equation near to 1 is 0.68217

Q14) Find the real root of the equation

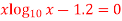
By the method of false position correct to four decimal places

A14) Let   

By hit and trail method

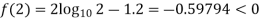
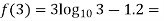0.23136 > 0

So, the root of the equation 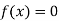lies between 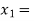2 and 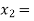3 and also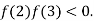

By Regula   Falsi Method

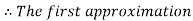
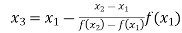
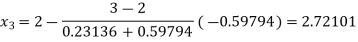
Now,

So, root of the equation 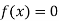  lies between 2.72101 and 3 and also

By Regula   Falsi Method

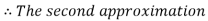
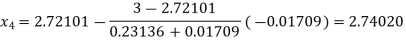
Now,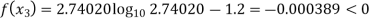

So, root of the equation 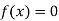  lies between 2.74020 and 3 and also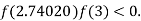

By Regula   Falsi Method

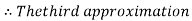
Now,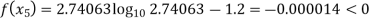

So, root of the equation 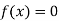  lies between 2.74063 and 3 and also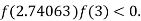

By Regula   Falsi Method

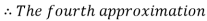
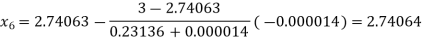
Hence the root of the given equation correct to four decimal places is 2.7406

Q15) Apply Regula Falsi Method to solve the equation

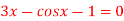
A15) Let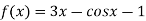 

By hit and trail

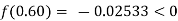
And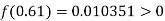

So, the root of the equation lies between 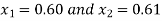and also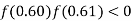

By Regula Falsi Method

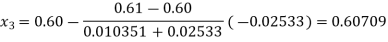
Now,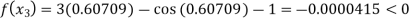

So, root of the equation 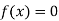  lies between 0.60709 and 0.61 and also

By Regula Falsi Method

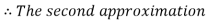
Now,

So, root of the equation 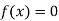  lies between 0.60710 and 0.61 and also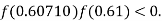

By Regula Falsi Method

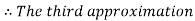
Hence the root of the given equation correct to five decimal place is 0.60710.

Q16) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: .

A16) Given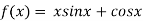

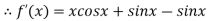
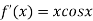
By Newton Raphson Method

= 

=

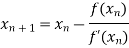
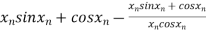
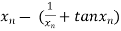
The initial approximation is 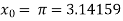in radian.

For n =0, the first approximation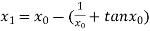

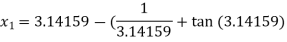
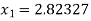
For n =1, the second approximation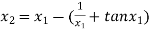

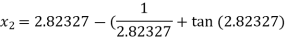
For n =2, the third approximation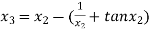

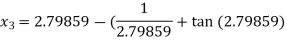
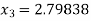
For n =3, the fourth approximation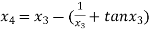

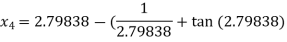
Hence the root of the given equation corrects to five decimal place 2.79838.

Q17) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 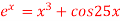near to 4.5

A17) Let

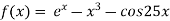
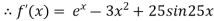
The initial approximation

By Newton Raphson Method

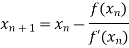
For n =0, the first approximation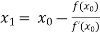

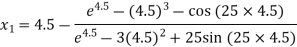
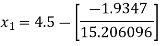
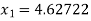
For n =1, the second approximation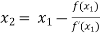

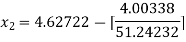
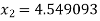
For n =2, the third approximation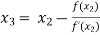

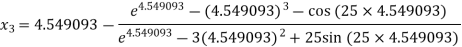
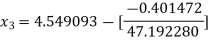
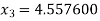
For n =3, the fourth approximation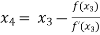

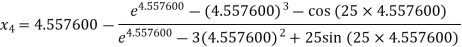
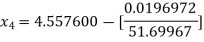
Hence the root of the equation correct to three decimal places is 4.5579

Q18) Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: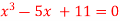

A18)

Let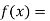

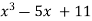
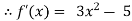
By Newton Raphson Method

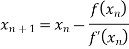
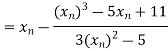
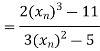
Let the initial approximation be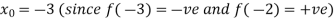

For n=0, the first approximation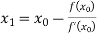

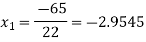
For n=1, the second approximation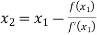

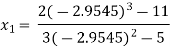
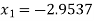
For n=2, the third approximation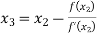

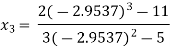
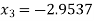
Since 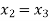therefore the root of the given equation correct to four decimal places is -2.9537

Q19) Find the root of the equation 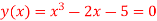which lies between 2 and 3

A19) Here let 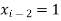, 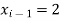and 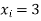. Then 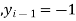and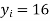

Hence

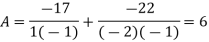
And

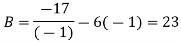
The quadratic equation is given by-

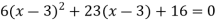
It gives the next approximation-

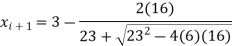
The positive sign is chosen as B is +ve,

Hence

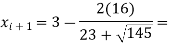
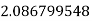
The error is calculated as-

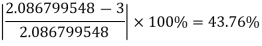
Here the error is large, so we do the next iteration-

And

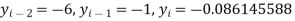
Now using these values, we get-

A = 5.086799558 and B = 10.96986336

The next approximation is-

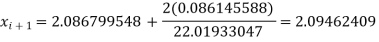
The error is 0.373553519%.

Q20) Find all the roots of polynomial equation 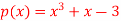rounded off to three decimal places.

Stop the iteration if |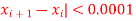

A20) The equation has three roots.

As there is only one change in the sign of the coefficient, by Descarts’ rule of sign the equation can have at most one positive real root.

The equation has no negative real roots since p(-x) = 0 has no change of sign of coefficients.

Here p(x) = 0 is of one degree, it has at least one real root.

So that the given equation has one positive real root and a complex pair.

Now let’s find the real roots by Birge-Vieta method-

The initial iteration is-

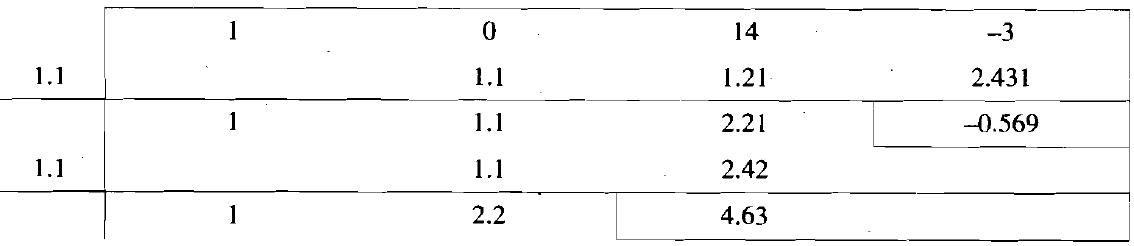
So that-

= 1.22289

Similarly

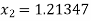
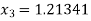
Here we see that 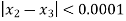so that we stop the iteration.

Hence the value of root is 1.213

Now we get the deflated polynomial of p(x).

In order to obtain deflated polynomial, we need to find the quadratic equation by using the final approximation. [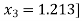

Here we notice p (1.213) = -0.0022,

That is, the magnitude of the error in satisfying p(x) = 0 is 0.0022.

We get-

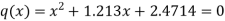
The roots of this quadratic equation are given by- [using quadratic equation]-

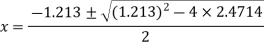
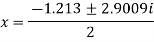
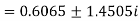
The three roots of the equation rounded off to three decimal places are 1.213, 0.6065+1.4505i and -0.6065 - 1.4505i