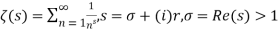UNIT 3
UNIT 3
Q1: Determine whether
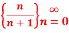
Solution: we consider,

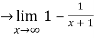 = 1-0 = 1
= 1-0 = 1
Thus the sequence converges to 1.
Q2: Determine whether  converges or diverges.If it converges, compute the limit.
converges or diverges.If it converges, compute the limit.
Solution:
Now we consider,
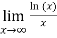
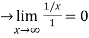
Therefore by using L’Hospital’s rule. The sequence converges to 0.
Q 3: Determine whether the following series converges or diverges
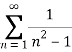
Solution: Consider the given series ie., 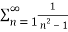
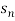 =
= 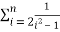 =
= -
- -
-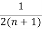
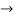
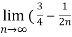 -
- ) =
) = 
Since ,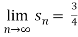
 therefore the given series is convergent.
therefore the given series is convergent.
Q 4:Determine whether the following series is diveregent or convergent
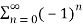
Solution: Given, 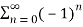
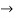 s0 =1
s0 =1
 s1 = 1-1=0
s1 = 1-1=0
 s2 = 1-1+1=1
s2 = 1-1+1=1
 s3 = 1-1+1-1=0
s3 = 1-1+1-1=0
Hence the series diverges since  doesn’t exist
doesn’t exist
Q 5: 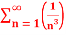 =
= 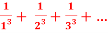
Here p = 3 so p>1 ,thus the given series converges.
 =
= 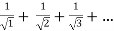
Here p= ie., p<1,thus the given series diverges
ie., p<1,thus the given series diverges
Q 6 :
=  +
+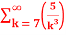
= -3. +5.
+5.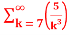
=-3. +5.
+5.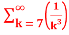
Therefore., here p=2 ,3 ie., p>1
Hence the given series converges
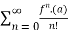 (x-a)n
(x-a)n
Q 7:Find the taylor series for the following:
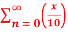
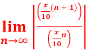 =
= 
 <1
<1
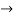 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
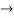 ROC =10
ROC =10
Q 8:  test for convergence
test for convergence
Solution: given f(x) = 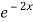
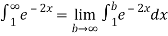
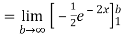
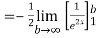
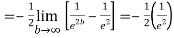
=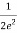
Thus, 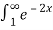 converges so by integral test
converges so by integral test 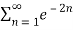 also converges.
also converges.
Q 9:Solve for convergence.
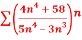
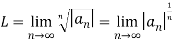

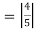
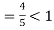
Q 10 :f’(x) = ln( ) ,
) , 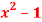 >0 x
>0 x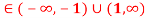
Solution:
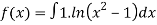
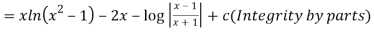
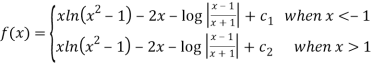
Q 11:Solve for convergence of the following
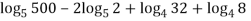
Solution: 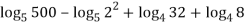
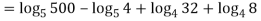
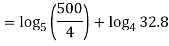

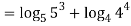
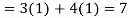
Q 12: 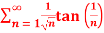 solve for convergence
solve for convergence
Given 
Note: 
For small x values ,thus for large n’s we have,
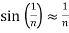
Thus,
For large n’s 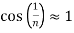
Thus, 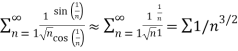
Which clearly converges
Q 13:Solve for convergence sin2x
Solution: we have sin2x =2sinx cosx…..(1)
Now ,we find the convergence for the given trigonometric function.
Let 2x=u , then x =u/2 now we substitute these values in equation (1)
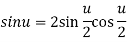
If 0<u<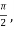 wwe can rewrite this as
wwe can rewrite this as
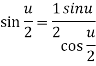
But u< , then
, then 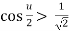 , and therefore
, and therefore
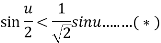
Let u=1. Since sin 1<1 , we find by using (*)
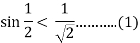
Let u = ½ . By using (*) again , and (1) we find that

Let u = 1/4 . By using(*) and (2) , we find that
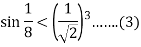
Continue .in general we have
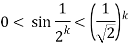
Thus
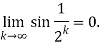
For 0 <x< , the since finction is an increasing function . It follows that
, the since finction is an increasing function . It follows that
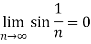
Q 14: Using complex form, find the Fourier series of the function
f(x) = sinnx = 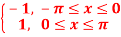
Solution:
We calculate the coefficients 
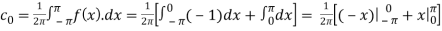
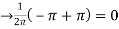

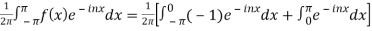
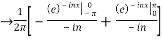 =
= 
=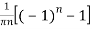
Hence the Fourier series of the function in complex form is
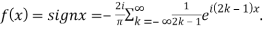
We can transform the series and write it in the real form by renaming as
n=2k-1,n=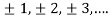
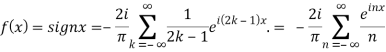
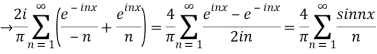
= 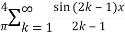
Q 15: Using complex form find the Fourier series of the function f(x) = x2, defined on the interval [-1,1]
Solution:
Here the half-period is L=1.Therefore, the co-efficient c0 is,
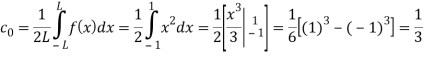
For n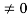
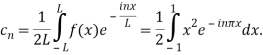
Integrating by parts twice, we obtain
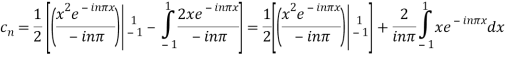
= 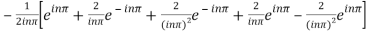
= 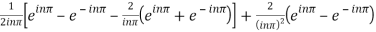
= 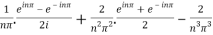 .
.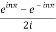
= 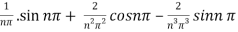 .
.
Q 16: consider 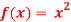 ,
, 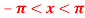
Solution: The Fourier expansion is,
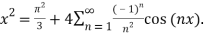
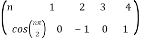
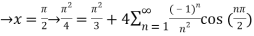
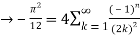
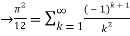
By Parseval’s formulae

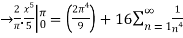
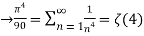
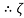 is Reiman Zeta function defined by:
is Reiman Zeta function defined by:

UNIT 3
UNIT 3
Q1: Determine whether
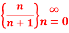
Solution: we consider,
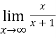
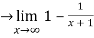 = 1-0 = 1
= 1-0 = 1
Thus the sequence converges to 1.
Q2: Determine whether 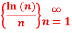 converges or diverges.If it converges, compute the limit.
converges or diverges.If it converges, compute the limit.
Solution:
Now we consider,
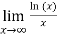
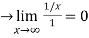
Therefore by using L’Hospital’s rule. The sequence converges to 0.
Q 3: Determine whether the following series converges or diverges
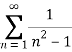
Solution: Consider the given series ie., 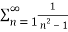
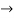
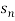 =
=  =
= -
-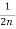 -
-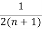
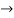
 -
-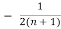 ) =
) = 
Since ,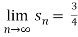
 therefore the given series is convergent.
therefore the given series is convergent.
Q 4:Determine whether the following series is diveregent or convergent

Solution: Given, 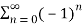
 s0 =1
s0 =1
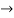 s1 = 1-1=0
s1 = 1-1=0
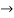 s2 = 1-1+1=1
s2 = 1-1+1=1
 s3 = 1-1+1-1=0
s3 = 1-1+1-1=0
Hence the series diverges since 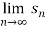 doesn’t exist
doesn’t exist
Q 5: 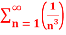 =
= 
Here p = 3 so p>1 ,thus the given series converges.
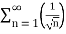 =
= 
Here p= ie., p<1,thus the given series diverges
ie., p<1,thus the given series diverges
Q 6 :
= 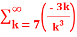 +
+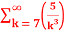
= -3.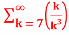 +5.
+5.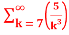
=-3.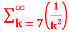 +5.
+5.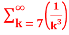
Therefore., here p=2 ,3 ie., p>1
Hence the given series converges
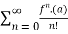 (x-a)n
(x-a)n
Q 7:Find the taylor series for the following:
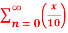
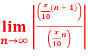 =
= 
 <1
<1
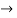 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
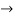 ROC =10
ROC =10
Q 8: 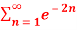 test for convergence
test for convergence
Solution: given f(x) = 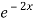
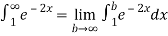
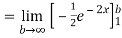

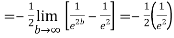
=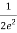
Thus, 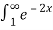 converges so by integral test
converges so by integral test 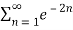 also converges.
also converges.
Q 9:Solve for convergence.
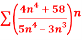
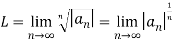



Q 10 :f’(x) = ln( ) ,
) ,  >0 x
>0 x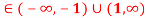
Solution:
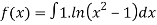
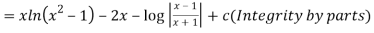
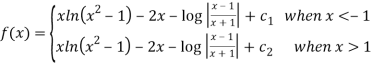
Q 11:Solve for convergence of the following
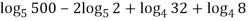
Solution: 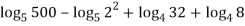
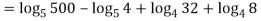



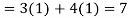
Q 12:  solve for convergence
solve for convergence
Given 
Note: 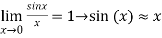
For small x values ,thus for large n’s we have,
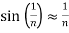
Thus,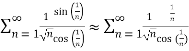
For large n’s 
Thus, 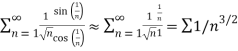
Which clearly converges
Q 13:Solve for convergence sin2x
Solution: we have sin2x =2sinx cosx…..(1)
Now ,we find the convergence for the given trigonometric function.
Let 2x=u , then x =u/2 now we substitute these values in equation (1)

If 0<u<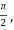 wwe can rewrite this as
wwe can rewrite this as
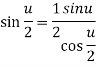
But u< , then
, then  , and therefore
, and therefore
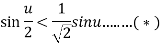
Let u=1. Since sin 1<1 , we find by using (*)
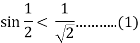
Let u = ½ . By using (*) again , and (1) we find that
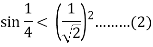
Let u = 1/4 . By using(*) and (2) , we find that
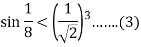
Continue .in general we have

Thus
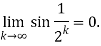
For 0 <x< , the since finction is an increasing function . It follows that
, the since finction is an increasing function . It follows that
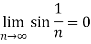
Q 14: Using complex form, find the Fourier series of the function
f(x) = sinnx = 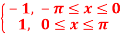
Solution:
We calculate the coefficients 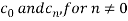
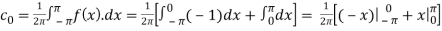
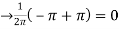
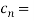

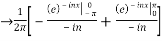 =
= 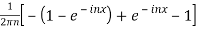
=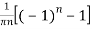
Hence the Fourier series of the function in complex form is
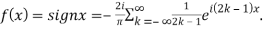
We can transform the series and write it in the real form by renaming as
n=2k-1,n=
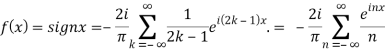
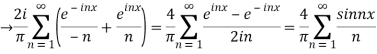
= 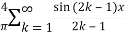
Q 15: Using complex form find the Fourier series of the function f(x) = x2, defined on the interval [-1,1]
Solution:
Here the half-period is L=1.Therefore, the co-efficient c0 is,
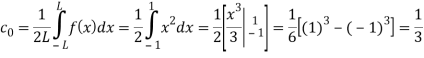
For n
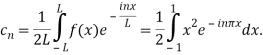
Integrating by parts twice, we obtain
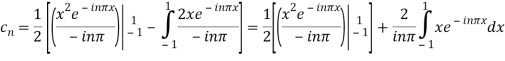
= 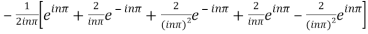
= 
= 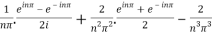 .
.
=  .
.
Q 16: consider 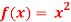 ,
, 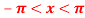
Solution: The Fourier expansion is,
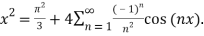
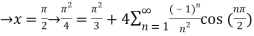
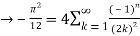
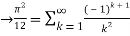
By Parseval’s formulae
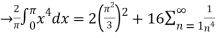
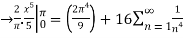
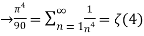
 is Reiman Zeta function defined by:
is Reiman Zeta function defined by: