Unit-5
Electrical Machines
Q1) For a p-type Ge ni = 2.1x1019m-3 density of boron =3.2x1023 atoms m-3. The electron and hole mobility are 0.4 and 0.2 m2V-1s-1. Calculate conductivity before and after addition of boron?
Sol: Before adding boron
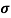 =q (p
=q (p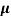 p+n
p+n n)
n)
= ni q ( p+
p+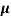 n) = 2.1x1019x1.6x10-19x(0.4+0.2)=2.016 S/m-1
n) = 2.1x1019x1.6x10-19x(0.4+0.2)=2.016 S/m-1
After adding boron
 =q p
=q p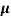 p
p
= 3.2x1023x1.6x10-19x0.2=10.24x103S/m-1
Q2) Determine the density of the donor atoms which have been added to the intrinsic Ge to make it a n-type material of resistivity 0.1x10-2ohm-m. Mobility of electron in n-type semiconductor is 0.5m2V-1s-1.
Sol: 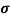 =q (n
=q (n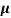 n)
n)
n= 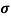 /q
/q n
n
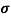 = 1/
= 1/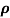
n= 1/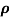 q
q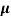 n = 1/(0.1x10-2x0.5x1.6x10-19) = 1.25x1022m-3
n = 1/(0.1x10-2x0.5x1.6x10-19) = 1.25x1022m-3
Q3) The intrinsic carrier density at room temperature in Ge is 3.4x1019m-3. If electron and hole mobilities are 0.4 and 0.2 m2V-1s-1 respectively. Calculate its resistivity?
Sol: 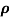 = 1/
= 1/
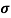 =ni q (
=ni q (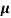 p+
p+ n) = 3.4x1019x 1.6x10-19(0.4+0.2) = 3.264S/m-1
n) = 3.4x1019x 1.6x10-19(0.4+0.2) = 3.264S/m-1
 = 1/
= 1/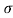 = 1/3.264 = 0.31ohm-m
= 1/3.264 = 0.31ohm-m
Q4) The electron and hole mobilities in In-Sb are 6 and 0.2m2V-1s-1 respectively. At room temperature resistivity of In-Sb is 2x10-4ohm-m. Find intrinsic carrier concentration assuming the material to be intrinsic?
Sol:  = 1/
= 1/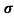
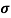 =ni q (
=ni q ( p+
p+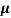 n)
n)
ni = 1/ q (
q ( p+
p+ n) = 1/2x10-4x1.6x10-19(6+0.2) = 5.04x1021m-3
n) = 1/2x10-4x1.6x10-19(6+0.2) = 5.04x1021m-3
Q5) An electric field of 90Vm-1 is applied to n-type semiconductor. Determine the current density in sample given electron mobility 0.4m2V-1s-1, n=5.9x1020m-3?
Sol: J=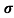 E
E
 = nq
= nq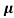 n = 5.9x1020x1.6x10-19x0.4=37.36S/m-1
n = 5.9x1020x1.6x10-19x0.4=37.36S/m-1
J=3.39x103
Q6) Determine the density of the donor atoms which have been added to the intrinsic Ge to make it a n-type material of resistivity 0.5x10-2ohm-m. Mobility of electron in n-type semiconductor is 0.8m2V-1s-1.
Sol: 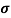 =q (n
=q (n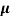 n)
n)
n= 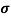 /q
/q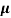 n
n
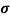 = 1/
= 1/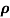
n= 1/ q
q n = 1/(0.5x10-2x0.8x1.6x10-19) = 1.56x1021m-3
n = 1/(0.5x10-2x0.8x1.6x10-19) = 1.56x1021m-3
Q7) In a CB IE= 2mA, IC=1.5mA. Calculate IB?
Sol: IE =IB+IC
2= IB+1.5
IB=0.5mA
Q8) In a CB current amplification factor is 0.9. If emitter current is 1.2mA. Determine the value of base current?
Sol: α = 0.9
IE =1.2mA
α = IC/ IE
IC = α IE =0.9 x 1.2 = 1.08mA
IE =IB+IC
1.2= IB+1.08
IB= 0.12mA
Q9) In a CB connection IC=1.0mA and IB= 0.02mA. Find the value of current amplification factor?
Sol: IE =IB+IC =1+0.02 = 1.02mA
α = IC/ IE
α = 1.0/1.02 = 0.98
Q10) In a CB connection the emitter current is 0.98mA. If the emitter circuit is open the collector current becomes 40 A. Find total collector current. α =0.92
A. Find total collector current. α =0.92
Sol: ICBO=40 A
A
IC =α IE+ICBO
= (0.92 x 0.98x10-3) + 40x10-6
IC =0.94mA
Q11) In a common base connection, α = 0.95. The voltage drop across 3 kΩ resistance which is connected in the collector is 2.5 V. Find the base current.
Sol: IC = 2.5/3000 = 0.83mA
α = IC/ IE
IE = IC/α =0.83/0.95=0.87mA
IE =IB+IC
0.87 =IB+0.83
IB=0.04mA
Q12) Find the value of β if (i) α = 0.9 (ii) α = 0.98 (iii) α = 0.99.
Sol: 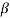 = α/1- α = 0.9/1-0.9 = 9
= α/1- α = 0.9/1-0.9 = 9
 = α/1- α = 0.98/1-0.98 = 49
= α/1- α = 0.98/1-0.98 = 49
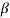 = α/1- α = 0.99/1-0.99 = 99
= α/1- α = 0.99/1-0.99 = 99
Q13) The collector leakage current in a transistor is 200 μA in CE arrangement. If nowthe transistor is connected in CB arrangement, what will be the leakage current? Given that β = 120.
Sol: ICEO=200 μA
 = 120
= 120
α =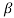 /1+
/1+ = 120/121=0.99
= 120/121=0.99
ICEO=ICBO/1- α
ICBO= 1.6μA
Q14) For a certain transistor, IB = 18 μA; IC = 2 mA and β = 60. Calculate ICBO.
Sol: IC = 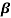 IB+ICEO
IB+ICEO
ICEO= IC -  IB= 2x10-3-(60x18x10-6) = 0.92mA
IB= 2x10-3-(60x18x10-6) = 0.92mA
α =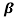 /1+
/1+ = 60/61=0.98
= 60/61=0.98
ICBO= (1- α) ICEO = (1-0.98) x 0.92=15.08μA
Q15) A single-phase half-wave rectifier is connected to a 50V RMS 50Hz AC supply. If the rectifier is used to supply a resistive load of 150 Ohms. Calculate the equivalent DC voltage developed across the load, the load current and power dissipated by the load. Assume ideal diode characteristics.
Sol: Maximum Voltage Amplitude, VM
VM = 1.414*VRMS = 1.414*50 = 70.7 volts
b) Equivalent DC Voltage, VDC
VDC = 0.318*VM = 0.318*70.7 = 22.5 volts
c) Load Current, IL
IL = VDC ÷ RL = 22.5/150 = 0.15A or 150mA
d) Power Dissipated by the Load, PL
PL = V*I or I2*RL = 22.5*0.15 = 3.4W
Q16) Four diodes are used to construct a single phase full-wave bridge rectifier circuit which is required to supply a purely resistive load of 2kΩ at 240 volts DC. Calculate the RMS value of the input voltage required, the total load current drawn from the supply, the load current passed by each diode and the total power dissipated by the load. Assume ideal diode characteristics.
Sol: Rectifier Supply Voltage, VRMS
VDC = 0.9*VRMS
VRMS = VDC/0.9 = 220/0.9 = 244.4 VRMS
b) Load Current, IL
IL = VDC/ RL = 240/1000 =120mA
c) Load Current Passed by Each Diode, ID
The load current is supplied by two diodes per cycle, thus:
ID = IL/2 = 0.12/2 =60mA
d) Power Dissipated by the Load, PL
PL = V*I or I2*RL = 240*0.12 = 28.8W