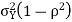Unit - 4
Bernoulli trials
Q1) What are Bernoulli trials?
A1)
Let a product is tested which may be defective or non-defective, let p be the probability of non-defective and q = 1 - p be the probability of defective product.
And let X be a random variable which takes 1 if success occurs and 0 if failure occurs.
Therefore-
P[X = 1] = p
P[X = 0] = q = 1- p
This experiment is known as a Bernoulli trial and the random variable X is a Bernoulli variable.
Conditions for Bernoulli tests
1. A finite number of tests.
2. Each trial must have exactly two results: success or failure.
3. The tests must be independent.
4. The probability of success or failure must be the same in each test.
Q2) 10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.
A2)
Probability of obtaining the head, p = 0.6
Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4
Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736
Q3) In an exam, 10 multiple-choice questions are asked where only one in four answers is correct. Find the probability of getting 5 out of 10 correct questions on an answer sheet.
A3)
Probability of obtaining a correct answer, p = 1414 = 0.25
Probability of obtaining a correct answer, q = 1 - p = 1 - 0.25 = 0.75
Probability of obtaining 5 correct answers, P (X = 5) = C105 (0.25) 5 (0.75) 5C510 (0.25) 5 (0.75) 5 = 0.05839920044
Q4) State Binomial distribution.
A4)
A discrete random variable X is said to be follow the binomial distribution with parameter n and p.
The probability of happening of an event r times exactly in n trials is-
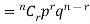
Q5) If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
A5)
Out of 10 ships one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 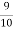
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P (5)

Q6) The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 men, now 60, at least seven will live to be 70?
A6)
The probability that a man aged 60 will live to be 70


Number of men= n = 10
Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10)
= P (7) + P (8) + P (9) + P (10) =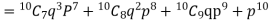
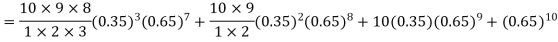
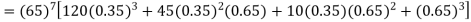
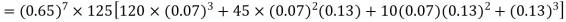
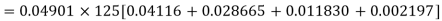

Q7) Find mean and variance of a binomial distribution with p = 1/4 and n = 10.
A7)
Here 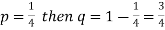
Mean = np = 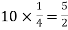
Variance = npq = 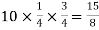
Q8) Define Poisson distribution.
A8)
Poisson distribution was derived in 1837 by a French mathematician Simeon D Poisson (1731-1840).
Poisson distribution is a particular limiting form of the Binomial distribution when p (or q) is very small and n is large enough.
Poisson distribution is
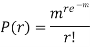
Where m is the mean of the distribution.
Q9) What is the moment generating function of Poisson distribution?
A9)
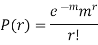
Let  be the moment generating function then
be the moment generating function then

Q10) What is the recurrence relationship of Poisson distribution?
A10)
By Poisson distribution

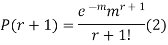
On dividing (2) by (1) we get
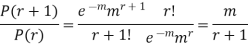
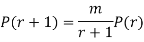
Q11) Suppose 3% of bolts made by a machine are defective, the defects occuring at random during production. If bolts are packaged 50 per box, find
(a) Exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
A11)
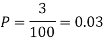
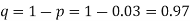
(a) Hence the probability for 5 defectives bolts in a lot of 50.
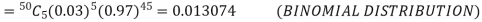
(b) To get Poisson approximation m = np =
Required Poisson approximation=
Q12) If cars arriving at workshop follow the Poisson distribution. If the average number of cars arrivals during a specified period of an hour is 2.
Find the probabilities that during the given hour-
1. No car arrive
2. At least two cars arrive.
A12)
Here the average of car arrivals is - 2
So that mean = 2
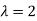
Let X be the number of cars arriving during the given hour,
By using Poisson distribution, we get-
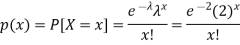
So that the required probability-
1. P [no car will arrive] = P [X = x] = 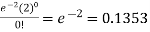
2. P [At least two cars will arrive] = P [X≥2] = P [X =2] + P [X = 3] + ……….
= 1 - P [[X =1] + P [X =0]]
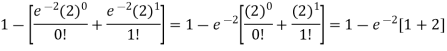

Q13) If a book has 600 pages and it has 40 printing mistakes. Assume that these mistakes are randomly distributed and x the number of mistakes per page follow Poisson distribution.
What is the probability that there will not be any mistake if 10 pages selected at random?
A13)
Here 
We get by using Poisson distribution-
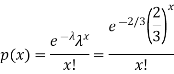
Then-
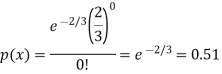
Q14) State hyper-geometric distribution.
A14)
Definition: A random variable X is said to follow the hypergeometric distribution with parameters N, M and n if it assumes only non-negative integer values and its probability mass function is given by
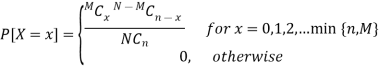
Where n, M, N are positive integers such that n ≤ N, M ≤ N.
Mean of the Hyper-geometric distribution is given as-
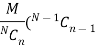
And the variance is
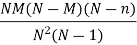
Q15) Find the mean and variance of a number on an unbiased die when thrown.
A15)
Suppose X be the number on an unbiased die when thrown,
Then X can take the values 1, 2, 3, 4, 5, 6 with
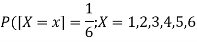
By uniform distribution, we have
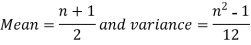
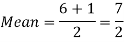
And
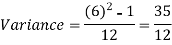
Q16) Find the coefficient of variation for the rectangular distribution in (0, 12).
A16)
Here a = 0, b = 12
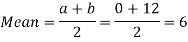

Then the SD will be-


Q17) Define normal distribution.
A17)
The concept of normal distribution was given by English mathematician Abraham De Moivre in 1733 but the concrete theory was given by Karl Gauss that is why sometime normal distribution is called Gaussian distribution.
Normal distribution is a continuous distribution. It is derived a s the limiting form of the Binomial distribution for large values of n and p and q are not very small.
The Normal distribution is given by the equation
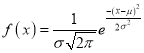 …. (1)
…. (1)
Where  mean,
mean, 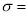 standard deviation,
standard deviation,  ,
, 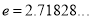

On substitution 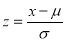 in (1), we get
in (1), we get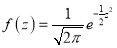 …. (2)
…. (2)
Here mean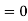 , standard deviation
, standard deviation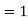
(2) is known as standard form of normal distribution.
Graph of a normal probability function-
The curve looks like bell-shaped curve. The top of the bell is exactly above the mean.
If the value of standard deviation is large then curve tends to flatten out and for small standard deviation it has sharp peak.
This is one of the most important probability distributions in statistical analysis.

Q18) What is the mean of the normal distribution?
A18)
Mean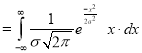 [Putting
[Putting  ]
]

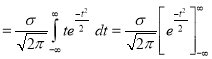

Q19) Write down the properties of normal curve.
A19)
Properties of the normal curve:
- The curve is symmetrical about the y – axis. The mean, median and mode coincide at the origin.
- The curve is drawn, if mean (origin of x) and standard deviation are given. The value of
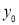 can be calculated from the fact that the area of the curve must be equal to the total number of observations.
can be calculated from the fact that the area of the curve must be equal to the total number of observations. - Y decreases rapidly as
 increases numericallu. The curve extends to infinity on either side of the origin.
increases numericallu. The curve extends to infinity on either side of the origin. - (a)
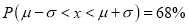
(b) 
(c) 
Hence (a) About 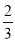 of the values will lie between
of the values will lie between 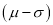 and
and 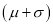 .
.
(b) About 95% of the values will lie between and
and 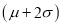 .
.
(c) About 99.7% of the values will lie between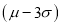 and
and 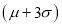 .
.
Q20) X is a normal variate with mean 30 and S.D. 5, find the probabilities that
(i) 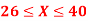
(ii) 
(iii) |X-30|≥5
A20)
We have μ =30 and 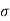 =5
=5

(i) When X = 26,z = -0.8, when X =40, z =-2
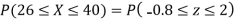

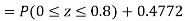
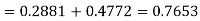
(ii) When X =45, z =3
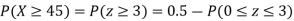

(iii) 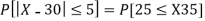
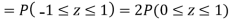

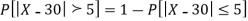
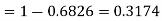
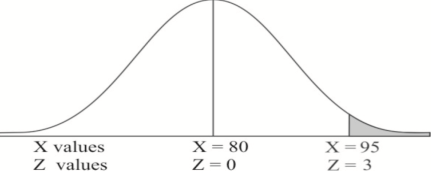
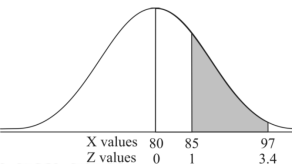
Q21) If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
A21)
The standard normal variate is – 
Now-
1. X = 95,
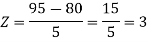
So that-

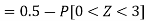


2. X = 72,

So that-
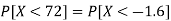
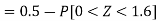
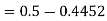
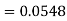

3. X = 85,
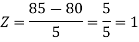
X = 97,
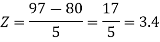
So that-
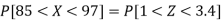


Q22) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed.
A22)
Here-

And
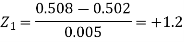
Area for non-defective washers = area between z = -1.2 to +1.2
= 2 area between z = 0 and z = 1.2
= 2 × 0.3849 = 0.7698 = 76.98%
Then percent of defective washers = 100 – 76.98 = 23.02 %
Q23) Let  be two independent N (0, 1) random variables. Define
be two independent N (0, 1) random variables. Define
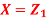
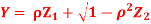
Where  is a real number in (-1, 1).
is a real number in (-1, 1).
- Show that X and Y are bivariate normal.
- Find the joint PDF of X and Y.
- Find
 (X,Y)
(X,Y)
A23)
First note that since 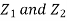 are normal and independent they are jointly normal with the joint PDF
are normal and independent they are jointly normal with the joint PDF
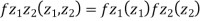
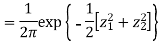
- We need to show aX + bY is normal for all. We have
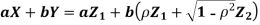
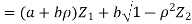
Which is the linear combination of  and thus it is normal.
and thus it is normal.
b. We can use the method of transformations (theorem 5.1) to find the joint PDF of X and Y. The inverse transformation is given by
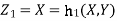
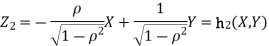
We have

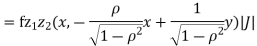
Where, 
Thus we conclude that
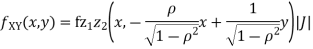
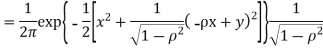
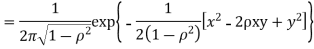
c. To find 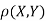 FIRST NOTE
FIRST NOTE

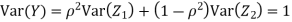
Therefore,

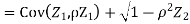

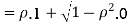
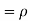
Q24) Let X and Y be jointly normal random variables with parameters  Find the conditional distribution of Y given X =x.
Find the conditional distribution of Y given X =x.
A24)
One way to solve this problem is by using the joint PDF formula since X N
N  we can use
we can use
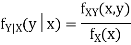
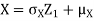

Thus given X=x, we have
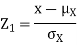
And,
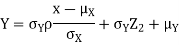
Since 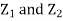 are independent, knowing
are independent, knowing 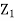 does not provide any information on
does not provide any information on  . We have shown that given X=x, Y is a linear function of
. We have shown that given X=x, Y is a linear function of  , thus it is normal. Ln particular
, thus it is normal. Ln particular


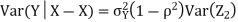
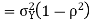
We conclude that given X=x, Y is normally distributed with mean 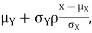 and variance
and variance