Unit - 3
Sample space & probability
Q1) Define random experiment.
A1)
An experiment in which we know all the possible outcomes but we can not say that or we can not predict that which of them will occur when we perform the experiment.
Suppose we toss a coin, we know that what are possible outcomes, it would be head or tail, but we do not know which one of these two will occur.
So tossing a coin is a random experiment.
Similarly, ‘Throwing a die’ and ‘Drawing a card from a well shuffled pack of 52 playing cards ‘are the examples of random experiment.
Q2) What are exhaustive and equally likely events?
A2)
Exhaustive Events or Sample Space: The set of all possible outcomes of a single performance of an experiment is exhaustive events or sample space. Each outcome is called a sample point.
In case of tossing a coin once, S = (H, T) is the sample space. Two outcomes - Head and Tail
- constitute an exhaustive event because no other outcome is possible.
Equally likely events: Two events are said to be ‘equally likely’, if one of them cannot be expected in preference to the other. For instance, if we draw a card from well-shuffled pack, we may get any card. Then the 52 different cases are equally likely.
Q3) 25 lottery tickets are marked with first 25 numerals. A ticket is drawn at random. Find the probability that it is a multiple of 5 or 7.
A3)
Let A be the event that the drawn ticket bears a number multiple of 5 and B be the event that it bears a number multiple of 7.
Therefore,
A = {5, 10, 15, 20, 25}
B = {7, 14, 21}
Here, as A 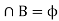
Therefore, A and B are mutually exclusive, and hence
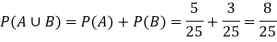
Q4) Define probability.
A4)
Classical Definition of Probability
Suppose there are ‘n’ exhaustive cases in a random experiment which is equally likely and mutually exclusive.
Let ‘m’ cases are favourable for the happening of an event A, then the probability of happening event A can be defined as-

Probability of non-happening of the event A is defined as-
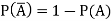
Note- Always remember that the probability of any events lies between 0 and 1.
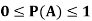
Note- Probability of an impossible event is always zero and that of certain event is 1.
The classical definition of probability fails if-
- The cases are not equally likely
- The number of exhaustive cases is indefinitely large
Q5) A bag contains 7 red and 8 black balls then find the probability of getting a red ball.
A5)
Here total cases = 7 + 8 = 15
According to the definition of probability,
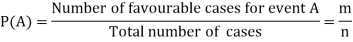
So that, here favourable cases- red balls = 7
Then,
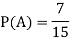
Q6) Define addition and multiplication law of probability-
A6)
Addition law-
If 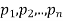 are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by
are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by 
Note-
If two events A and B are not mutually exclusive then the probability of the event that either A or B or both will happen is given by-

Multiplication law-
For two events A and B-
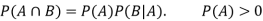
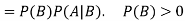
Here 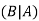 is called conditional probability of B given that A has already happened.
is called conditional probability of B given that A has already happened.
Now-
If A and B are two independent events, then-
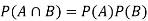
Because in the case of independent events- 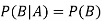
Q7) A die is rolled. If the outcome is a number greater than three. What is the probability that it is a prime number?
A7)
The sample space is- S = {1, 2, 3, 4, 5, 6}
Let A be the event that an outcome is a number that is greater than three and B be the event that it is a prime.
So that-
A = {4, 5, 6} and B = {2, 3, 5} and hence 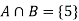
P(A) = 3/6, P(B) = 3/6 and 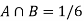
Now the required probability-
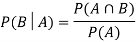
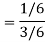

Q8) A can hit a target 3 times in 5 shots, B 2 times in 5 shots, and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.
What is the probability that:
1. Two shots hit
2. At least two shots hit
A8)
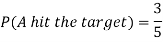
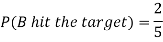
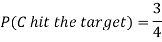
1. Now probability that 2 shots hit the target-
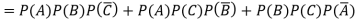
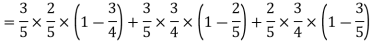
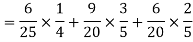

2. Probability of at least two shots hitting the target
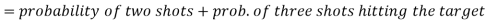
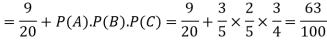
Q9) A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
A9)
We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for 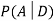 . We know:
. We know:
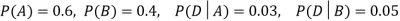
Now,
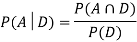
So we need
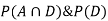
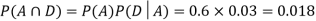
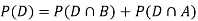
Since, D is the union of the mutually exclusive events 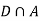 and
and 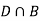 (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)

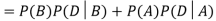
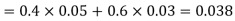
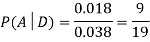
Q10) What do you understand by independent events?
A10)
Events are said to be independent if happening or non-happening of any one event is not affected by the happening or non-happening of other events. For example, if a coin is tossed certain number of times, then happening of head in any trial is not affected by any other trial i.e., all the trials are independent.
Two events A and B are independent if and only if P(B|A) = P(B) i.e., there is no relevance of giving any information. Here, if A has already happened, even then it does not alter the probability of B.
If A and B are independent events then-

(Two disjoint events are not independent.)
Independence implies that
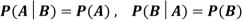
Knowing that outcome is in B does not change your perception of the outcome’s being in A.
Note-
- Mutually exclusive events can never be independent.
- If events A and B are independent then-
- A and B’ are independent
- A’ and B are independent
- A’ and B’ are independent
Q11) A class consists of 10 boys and 40 girls. 5 of the students are rich and 15 students are brilliant. Find the probability of selecting a brilliant rich boy.
A11)
Let A be the event that the selected student is brilliant, B be the event that he/she is rich and C be the event that the student is boy.
P(A) = 15/50, P(B) = 5/50 and P(C) = 10/50,
Hence the required probability- [ A, B, C are independent events]
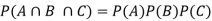
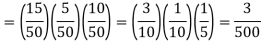
Q12) A die is rolled. If the outcome is a number greater than 3, what is the probability that it is a prime number?
A12)
The sample space of the experiment is
S = {1, 2, 3, 4, 5, 6}
Let A be event that the outcome is a number greater than 3 and B be the event that it is a prime number.
A = {4, 5, 6}, B = {2, 3, 5} and hence

P(A) = 3/6, P(B) = 3/6, 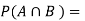 1/6.
1/6.
The required probability = P(B|A)
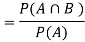
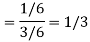
Q13) State Bayes theorem.
A13)
Let S be a sample space and 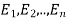 be n mutually exclusive events with P (
be n mutually exclusive events with P (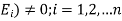 .
.
Let A be an event which is a sub-set of 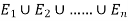 with P(A)>0, then-
with P(A)>0, then-
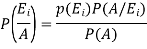
Where i = 1, 2, ……. , n
And 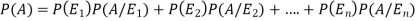 [which is the law of total probability]
[which is the law of total probability]
Q14) A person speaks the truth 3 out of 4 times. A die is thrown. She reports that there are five. What is the chance there is 5?
A14)
Let 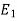 be the event that the person speaksthe truth,
be the event that the person speaksthe truth, 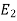 be the event that she tells lie and A be the event that she reports a five.
be the event that she tells lie and A be the event that she reports a five.
So that-
By the law of total probability-
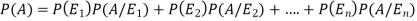
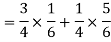
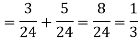
Now we have to find- 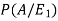
By using Bayes theorem-
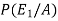 =
= 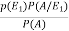
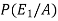 =
= 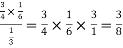
Which is the required probability.
Q15) What is discrete random variable and its distribution function?
A15)
A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.
Note- if a random variable takes a finite set of values, it is called discrete and if a random variable takes an infinite number of uncountable values, it is called continuous variable.
Discrete probability distributions-
Let X be a discrete variate which is the outcome of some experiments. If the probability that X takes the values of x is 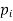 , then-
, then-

Where-
1. 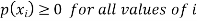
2. 
The set of values 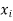 with their probabilities
with their probabilities 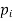 makes a discrete probability distribution of the discrete random variable X.
makes a discrete probability distribution of the discrete random variable X.
Probability distribution of a random variable X can be exhibited as follows-
X |  | 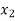 | 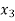 |
P(x) | 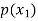 | 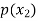 | 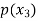 |
Q16) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
A16)
Let be the number of heads in the toss of three coins
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P [X= 0] = P[TTT] = 1/8
P[X = 1] = P [HTT, THH, TTH] = 3/8
P [X = 2] = P [HHT, HTH, THH] = 3/8
P [X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X |  | 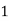 |  |  |
P(x) |  |  |  |  |
Q17) A random variate X has the following probability function
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P (x) | 0 | k | 2k | 2k | 3k | 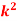 |  |  |
(i) Find the value of the k.
(ii) 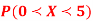
A17)
i) If X is a random variable then
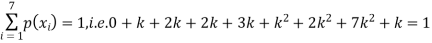
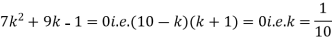
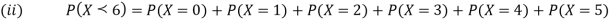
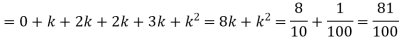
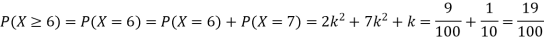
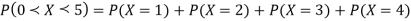

Q18) Show that the following function can be defined as a density function and then find  .
.


A18)
Here
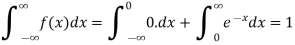
So that, the function can be defined as a density function.
Now.
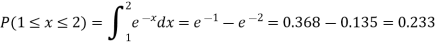
Q19) Let X be a continuous random variable with PDF given by

If 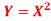 , find the CDF of Y.
, find the CDF of Y.
A19)
First, we note that 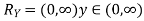 , we have
, we have
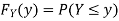
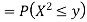
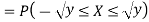
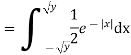

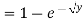
Thus, 
Q20) Find the expectations of the number of an unbiased die when thrown.
A20)
Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[ X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-

So that-

Q21) The frequency distribution of a measurable characteristic varying between 0 and 2 is as under
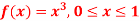
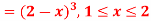
Calculate two standard deviation and also the mean deviation about the mean.
A21)
Total frequency N =
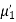 (About the origin) =
(About the origin) =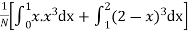
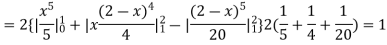
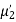 (About the origin) =
(About the origin) = 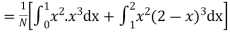
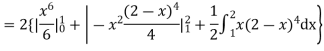
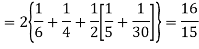
Hence, 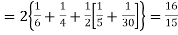
i.e., standard deviation 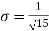
Mean derivation about the mean
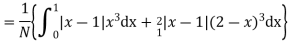
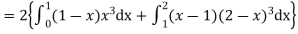
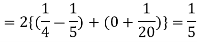
Q22) What are central moments?
A22)
Moments about mean [Central moments]
If x1, x2, ..., xn are the values of the variable under consideration, the r’th moment 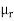 about mean is defined as
about mean is defined as
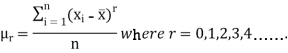
Moments about mean for a frequency distribution
If x1, x2, ..., xn are the values of a variable x with the corresponding frequencies f1, f2, ..., fn respectively then r’th moment 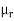 about the mean is defined as
about the mean is defined as
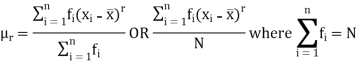
In particular
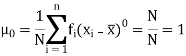
Hence for any distribution, note it here
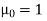
Now for r = 1
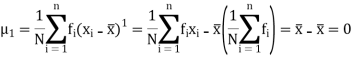
Hence for any distribution,
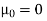
For r = 2

Similarly

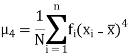
And so on.
Q23) Explain moment generating function.
A23)
The moment generating function of the variate 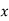 about
about 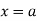 is defined as the expected value of
is defined as the expected value of 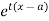 and is denoted
and is denoted 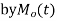 .
.
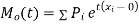
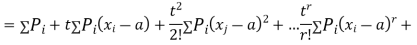
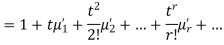
Where 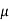 , ‘is the moment of order
, ‘is the moment of order 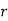 about
about 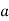
Hence 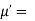 coefficient of
coefficient of  or
or 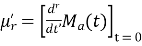
Again
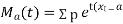 )
) 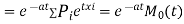
Thus, the moment generating function about the point 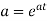 moment generating function about the origin.
moment generating function about the origin.