Unit – 4
Learning Methods
Q1) What is statistical learning?
A1) Statistical learning
● Learn probabilistic theories of the world from experience.
● We focus on the learning of Bayesian networks
● More specifically, input data (or evidence), learn probabilistic theories of the world (or hypotheses)
View learning as Bayesian updating of a probability distribution over the hypothesis space
H is the hypothesis variable, values h1, h2, . . ., prior P(H) jth observation dj gives the outcome of random variable Dj training data d = d1, . . . , dN
Given the data so far, each hypothesis has a posterior probability:
P(hi|d) = αP(d|hi) P(hi)
where P(d|hi) is called the likelihood
Predictions use a likelihood-weighted average over all hypotheses:
P(X|d) = Σi P (X|d, hi) P(hi|d) = Σi P(X|hi) P(hi|d)
Example
Suppose there are five kinds of bags of candies: 10% are h1: 100% cherry candies
20% are h2: 75% cherry candies + 25% lime candies 40% are h3: 50% cherry candies + 50% lime candies 20% are h4: 25% cherry candies + 75% lime candies 10% are h5: 100% lime candies
Then we observe candies drawn from some bag:
What kind of bag is it? What flavour will the next candy be?
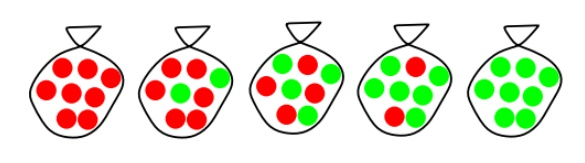
Fig 1: Example
1.The true hypothesis eventually dominates the Bayesian prediction given that the true hypothesis is in the prior
2.The Bayesian prediction is optimal, whether the data set be small or large[?] On the other hand
Q2) Explain all of them. A. Learning with Complete Data
B. Learning with Hidden Variables
C. Learning by taking advice
A2) A. Learning with complete data
The easiest task in the development of statistical learning algorithms is parameter learning using complete data. Finding the numerical parameters for a probability model with a fixed structure is a parameter learning task. For example, in a Bayesian network with a certain structure, we would be interested in learning the conditional probabilities.
When each data point has values for every variable in the probability model being trained, the data is full. The problem of learning the parameters of a complex model is substantially simplified when there is complete data. We'll also take a quick look at the issue of learning structure.
B. Learning with Hidden Variables
Many real-world situations have hidden variables (also known as latent variables) that aren't visible in the data that can be learned. Medical records, for example, frequently include the observed symptoms, the treatment used, and possibly the treatment's outcome, but they rarely include a firsthand observation of the disease itself! “Why not design a model without the sickness if it is not observed?” one could wonder. The solution can be found in Figure, which depicts a modest, fake heart disease diagnostic model. There are three predisposing factors and three symptoms that can be observed (which are too depressing to name).
Assume that each variable can take three different forms (e.g., none, moderate, and severe). The network in (a) becomes the network in (b) when the hidden variable is removed; the total number of parameters grows from 78 to 708. As a result, the number of parameters required to specify a Bayesian network can be drastically reduced using latent variables. As a result, the amount of data required to learn the parameters can be drastically reduced.
Hidden variables are important, but they do complicate the learning problem. In Figure, for example, it is not obvious how to learn the conditional distribution for Heart Disease, given its parents, because we do not know the value of Heart Disease in each case; the same problem arises in learning the distributions for the symptoms.
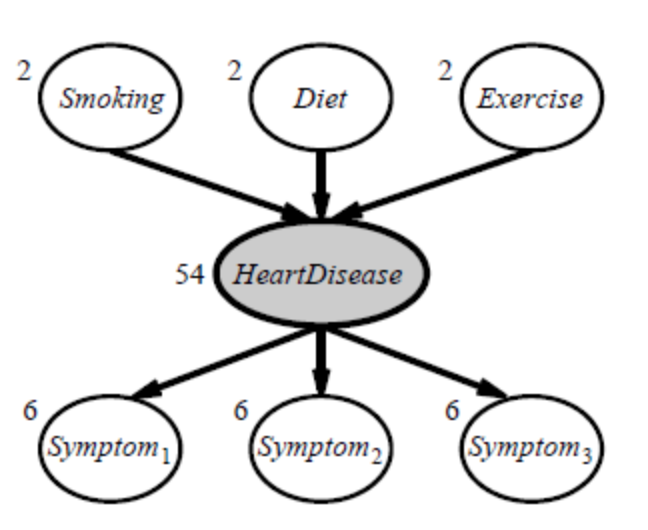
Fig 2: A simple diagnostic network for heart disease, which is assumed to be a hidden variable
C. Learning by taking advice
● This is the simplest and most straightforward method of learning.
● In this type of learning, a programmer creates a program that instructs the machine to accomplish a task. The system will be able to accomplish new things once it has been learned (i.e., programmed).
● There are also a variety of sources for getting guidance, such as humans (experts), the internet, and so on.
● This form of learning, on the other hand, necessitates more inference than rote learning.
● The dependability of the information source is always taken into account as the stored knowledge in the knowledge base is translated into an operational form.
● The programs shall operationalize the advice by turning it into a single or multiple expressions that contain concepts and actions that the program can use while under execution.
● This ability to operationalize knowledge is very critical for learning. This is also an important aspect of Explanation Based Learning (EBL).
Q3) Write short notes on rote learning?
A3) Rote learning
● The most basic learning activity is rote learning.
● It's also known as memorizing because the knowledge is simply copied into the knowledge base without any modifications. Rules and facts can be entered directly.
● The term "knowledge base" refers to knowledge that has been captured.
● Ontology development in the traditional sense.
● To boost performance, data caching is used.
● This strategy can save a lot of time because computed values are saved.
● In complicated learning systems, the rote learning technique can be used if sophisticated techniques are used to utilize the recorded values faster and there is a generalization to keep the number of stored information to a manageable level.
● Checkers-playing program, for example, uses this technique to learn the board positions it evaluates in its look-ahead search.
● Depends on two important capabilities of complex learning systems:
Q4) Describe Learning in Problem-solving?
A4) Learning in Problem-solving
When the program does not learn from advice, it can learn by generalizing from its own experiences.
● Learning by parameter adjustment
● Learning with macro-operators
● Learning by chunking
● The unity problem
Learning by parameter adjustment
● In this case, the learning system relies on an evaluation technique that aggregates data from multiple sources into a single static summary.
● Demand and production capacity, for example, might be integrated into a single score to indicate the likelihood of increased production.
● However, determining how much weight should be given to each component a priori is challenging.
● The correct weight can be discovered by estimating the correct settings and then letting the computer adjust them based on its experience.
● The weights of features that appear to be good indicators of overall performance will be increased, while the weights of features that do not will be dropped.
● When there is a lack of knowledge, this type of learning technique comes in handy.
● For example, in game programs, elements like piece advantage and mobility are merged into a single score to determine whether a specific board position is desired. This single score is nothing more than information obtained by the program through calculation.
● This is done by programs in their static evaluation functions, which integrate a number of elements into a single score. The following is the polynomial form of this function:
● 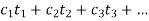
● The values of the qualities that contribute to the evaluation are represented by the t terms. The coefficients or weights that are assigned to each of these values are referred to as the c terms.
● It can be difficult to decide on the correct value to give each weight while building programs. As a result, the primary principle of parameter adjustment is to:
○ Begin with a rough estimate of the proper weight values.
○ On the basis of acquired experience, adjust the program's weight.
○ The weights of features that appear to be good forecasters will be increased, while the weights of features that appear to be bad predictors will be decreased.
● The following are important aspects that influence performance:
○ When should a coefficient's value be increased and when should it be reduced?
■ The coefficients of terms that properly predicted the end result should be increased, while the coefficients of bad predictors should be reduced.
■ Credit assignment system is the problem of properly assigning responsibility to each of the stages that led to a single outcome.
○ How much should the value be altered?
● Learning procedure is a variety of hill-climbing.
● This method is very useful in situations where very little additional knowledge is available or in programs in which it is combined with more knowledge intensive methods.
Learning with Macro-Operators
● Macro-operators are groups of actions that can be handled as a whole.
● After a problem has been solved, the learning component saves the computed plan as a macro-operator.
● The preconditions are the initial conditions of the problem that was just solved, and the postconditions are the results of the problem.
● The issue solver makes effective use of the knowledge learned from prior experiences.
● The issue solver can even tackle other problems by generalizing macro-operations. All the constants in the macro-operators are replaced with variables to achieve generalization.
● Even though the various operators that make up the macro-operator generate numerous undesired local changes, it can produce a minor global impact in the world.
● We can gain domain-specific knowledge in the form of macro-operators.
Learning by Chunking
● Learning with macro-operators is akin to chunking. It's typically employed by problem-solving systems that use production systems.
● A production system is made up of a set of rules in the form of if-then statements. That is, given a specific situation, what measures should be taken. If it's raining, for example, bring an umbrella.
● Problem solvers solve problems by applying the rules. Some of these rules may be more useful than others and the results are stored as a chunk.
● Chunking can be used to learn general search control knowledge.
● Chunks learned in the beginning of problem solving, may be used in the later stage. The system keeps the chunk to use in solving other problems.
The utility problem
● When knowledge is learnt in an attempt to improve a system's performance, it instead damages it. This is known as the utility problem in learning systems.
● The issue can be found in a variety of AI systems, although it is most commonly seen in speedup learning. Speedup learning methods are designed to help people improve their problem-solving skills by teaching them control principles. If these systems are allowed to learn unrestrictedly, they frequently exhibit the unwanted trait of actually slowing down.
● Each control rule has a positive utility (increase performance), but when combined, they have a negative utility (decrease performance) (degrade performance).
● One of the causes of the utility problem is the serial nature of current hardware. The more control rules that speedup learning systems acquire, the longer it takes for the system to test them on each cycle.
● Such utility considerations apply to a wide range of learning problems.
● The PRODIGY program maintains a utility measure for each control rule. This measure takes into account the average savings provided by the rule, the frequency of its application and the cost of matching it.
● If a proposed rule has a negative utility, it is discarded or forgotten.
Q5) Define inductive learning?
A5) Inductive learning
Inductive Learning in supervised learning we have a set of {xi, f (xi)} for 1≤i≤n, and our aim is to determine 'f' by some adaptive algorithm. It is a machine learning approach in which rules are inferred from facts or data. In logic, reasoning from the specific to the general Conditional or antecedent reasoning. Theoretical results in machine learning mainly deal with a type of inductive learning called supervised learning. In supervised learning, an algorithm is given samples that are labeled in some useful way.
In case of inductive learning algorithms, like artificial neural networks, the real robot may learn only from previously gathered data. Another option is to let the bot learn everything around him by inducing facts from the environment. This is known as inductive learning. Finally, you could get the bot to evolve, and optimize its performance over several generations.
f(x) is the target function
An example is a pair [x, f(x)]
Some practical examples of induction are:
● Credit risk assessment.
○ The x is the property of the customer.
○ The f(x) is credit approved or not.
● Disease diagnosis.
○ The x are the properties of the patient.
○ The f(x) is the disease they suffer from.
● Face recognition.
○ The x are bitmaps of people’s faces.
○ The f(x) is to assign a name to the face.
● Automatic steering.
○ The x are bitmap images from a camera in front of the car.
○ The f(x) is the degree the steering wheel should be turned.
Two perspectives on inductive learning:
● Learning is the removal of uncertainty. Having data removes some uncertainty. Selecting a class of hypotheses we are removing more uncertainty.
● Learning is guessing a good and small hypothesis class. It requires guessing. We don’t know the solution, we must use a trial-and-error process. If you know the domain with certainty, you don’t need learning. But we are not guessing in the dark.
Q6) Write about Explanation-based Learning?
A6) Explanation-based Learning
Explanation-based learning allows you to learn with just one training session. Rather than taking multiple instances, the emphasis is on explanation-based learning to memorize a single, unique example. Take, for example, the Ludo game. In a Ludo game, the buttons are usually four different colors. There are four different squares for each color.
Assume red, green, blue, and yellow are the primary colors. As a result, this game can only have a maximum of four players. Two members are considered for one side (for example, green and red), while the other two are considered for the opposing side (suppose blue and yellow). As a result, each opponent will play his own game.
The four members share a square-shaped tiny box with symbols numbered one through six. The lowest number is one, and the greatest number is six, for which all procedures are completed. Any member of the first side will always try to attack a member of the second side, and vice versa. Players on one side can attack players on the opposing side at any time during the game.
Similarly, all of the buttons can be hit and rejected one by one, with one side eventually winning the game. The players on one side can attack the players on the opposing side at any time. As a result, a single player's performance may have an impact on the entire game.
Explanation-based generalization (EBG) is an explanation-based learning method described by Mitchell and colleagues (1986). It contains two steps: the first is to explain the method, and the second is to generalize the method. The domain theory is utilized in the first stage to remove all of the unnecessary elements of training examples in relation to the goal notion. The second step is to broaden the explanation as much as feasible while keeping the goal concept in mind.
Q7) What is discovery?
A7) Discovery
Theory Driven Discovery - AM (1976)
AM is a program that teaches basic mathematics and set theory ideas.
AM has two inputs:
● a description of some set theory notions (in LISP form). Set union, intersection, and the empty set are examples.
● Instructions on how to solve math problems. Consider functions.
How does AM work?
AM employs many general-purpose AI techniques:
● A frame-based representation of mathematical concepts.
AM can create new concepts (slots) and fill in their values.
● Heuristic search employed
250 heuristics represent hints about activities that might lead to interesting discoveries.
How to employ functions, create new concepts, generalization etc.
● Hypothesis and test-based search.
● Agenda control of discovery process
AM discovered
● Integers – The elements of this set may be counted, and here is the image of this counting function — the integers — an intriguing set in and of itself.
● Addition – The counting function of the union of two disjoint sets
● Multiplication – Following the discovery of addition and multiplication as time-consuming set-theoretic operations, more effective hand-written descriptions were created.
● Prime number – Number factorization and numbers with only one factor have been identified.
● Golbach's Conjecture – The sum of two primes can be stated as an even number. For example, 28 = 17 + 11.
● Maximally Divisible Numbers – integers with as many variables as possible When a number k has more factors than any integer less than k, it is said to be maximally divisible. For example, the number 12 has six divisors: 1,2,3,4,6,12.
Data Driven Discovery -- BACON (1981)
Many discoveries are made from observing data obtained from the world and making sense of it -- E.g., Astrophysics - discovery of planets, Quantum mechanics - discovery of subatomic particles.
BACON is an attempt at providing such an AI system. BACON system outline:
● Starts with a set of variables for a problem.
○ E.g., BACON was able to derive the ideal gas law. It started with four variables p - gas pressure, V -- gas volume, n -- molar mass of gas, T -- gas temperature. Recall pV/nT = k where k is a constant.
● Values from experimental data from the problem are inputted.
● BACON holds some constant and attempts to notice trends in the data.
● Inferences made.
BACON has also been applied to Kepler's 3rd law, Ohm's law, conservation of momentum and Joule's law.
Clustering
● Clustering is the process of dividing data into numerous new categories.
● It's a popular descriptive assignment in which the goal is to find a small number of categories or clusters to characterize the data. We might want to cluster dwellings to uncover distribution patterns, for example.
● Clustering is the technique of categorizing a collection of physical or abstract things into groups of related objects.
● A cluster is a group of data objects that are similar to one another inside the cluster but different from objects in other clusters. Clustering analysis aids in the division of a large number of objects into meaningful groups.
● The task of clustering is to maximize the intra-class similarity and minimize the interclass similarity.
○ Given N k-dimensional feature vectors, find a "meaningful" partition of the N examples into c subsets or groups
○ Discover the "labels" automatically
○ c may be given, or "discovered“
○ much more difficult than classification, since in the latter the groups are given, and we seek a compact description
AutoClass
● AutoClass is a clustering algorithm for determining optimal classes in huge datasets based on the Bayesian approach.
● Given a set X= {X1, …, Xn} of data instances Xi with unknown classes, the goal of Bayesian classification is to search for the best class description that predicts the data in a model space.
● The probability of belonging to a class is expressed.
● An instance is not assigned to a single class, but it has a chance of belonging to each of the available classes (represented as weight values).
● AutoClass evaluates the probability of each instance belonging to each class C, and then assigns each instance a set of weights wij= (Ci / SjCj).
● For estimating the class model, weighted statistics relevant to each term of the class likelihood are generated.
● The classification step is the most computationally intensive. It computes the weights of every instance for each class and computes the parameters of a classification.
Q8) Write about analogy?
A8) Analogy
Learning by analogy entails gaining new knowledge about an input entity by transferring it from a similar entity that is already known.
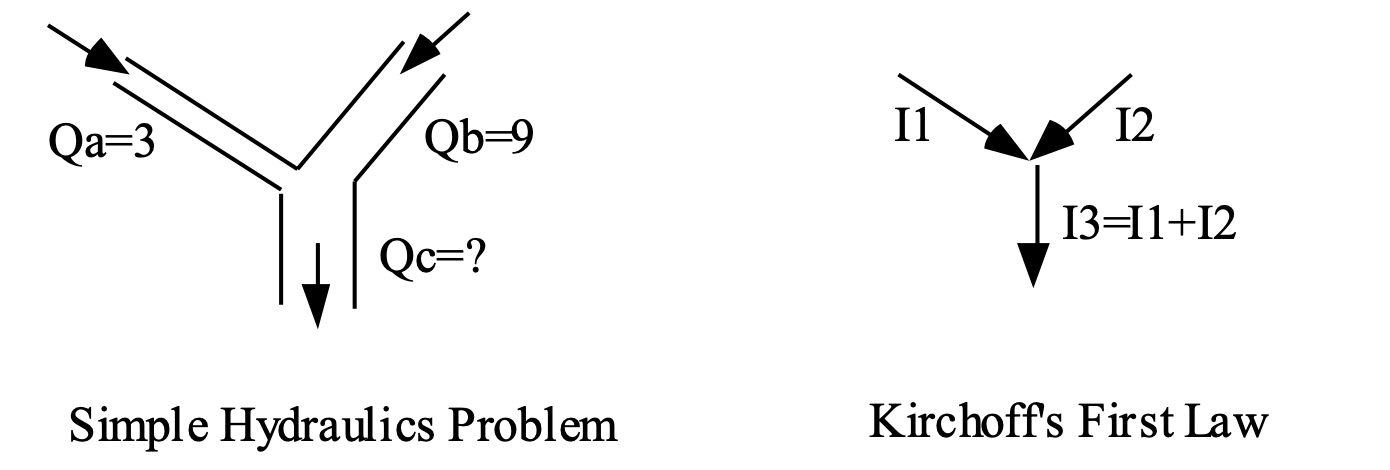
Fig 3: Analogies
Hydraulic laws, like Kirchoff's laws and Ohm's law, can be inferred from analogies.
Central intuition supporting learning by analogy:
If two entities are similar in some respects then they could be similar in other respects as well.
Examples of analogies:
Pressure Drop is like Voltage Drop
A variable in a programming language is like a box.
Transformational analogy
Find a similar solution and adapt it to the current scenario, making appropriate substitutes as needed.
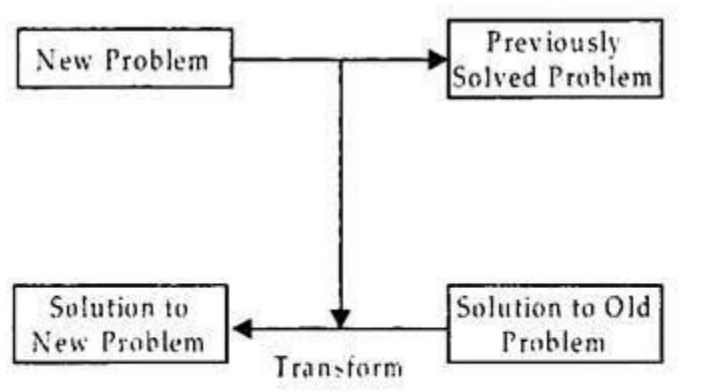
Fig 4: Transformational analogy
Example: Geometry
We can make similar assertions regarding angles if you know about line segment lengths and a proof that certain lines are equal.
We know that lines RO = NY and angles AOB = COD
We have seen that RO + ON = ON + NY - additive rule.
So we can say that angles AOB + BOC = BOC + COD
So by a transitive rule line RN = OY So similarly angle AOC = BOD
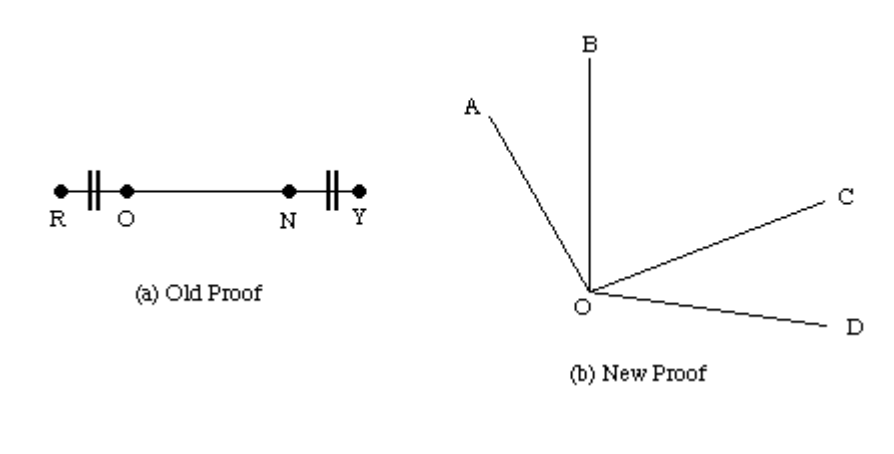
Fig 5: Example
Derivational analogy
If two problems match within a specific threshold, according to a given similarity metric, they share significant elements.
The retrieved problem's solution is tweaked incrementally until it meets the new problem's specifications.
The end answer is the only thing that matters in a transformational comparison. It doesn't matter how the problem was addressed. The steps involved in the problem solution's history are frequently relevant.
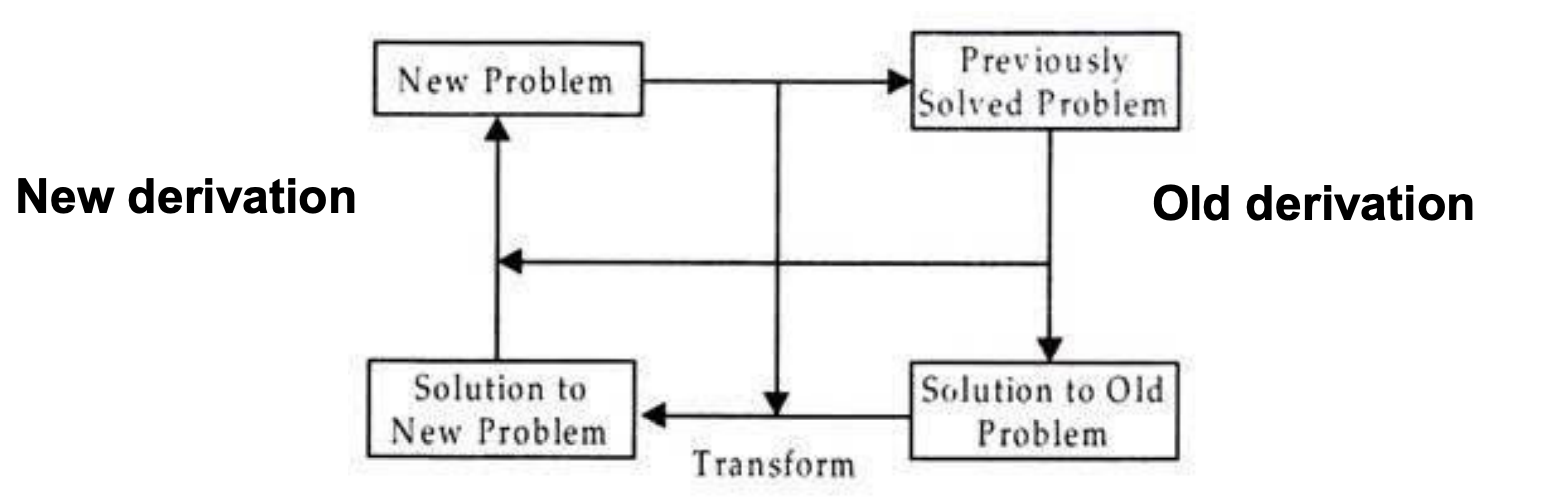
Fig 6: derivational analogy
Q9) Write short notes on formal learning theory?
A9) Formal learning theory
● Valiant's Theory of the Learnable categorizes situations according to how difficult they are to learn.
● Formally, a device can learn a concept if it can generate an algorithm that will correctly classify future cases with probability 1/h given positive and negative examples.
● Complexity of learning a function is decided by three factors:
○ The error tolerance (h)
○ The number of binary features present in the example (t)
○ Size of rules necessary to make the discrimination (f)
● The system is considered to be trainable if the number of training examples is a polynomial in h, t, and f.
● Learning feature descriptions is an example.
● The usage of knowledge will be quantified using mathematical theory.
Gray? | Mammal? | Large? | Vegetarian? | Wild? |
|
|
+ + + - + + | + + + + - + | + - + + + + | + - + + - + | + + + + + - | + + - - - + | Elephant Elephant Mouse Giraffe Dinosaur Elephant |
Q10) What do you mean by neural net learning?
A10) Neural Net
A neural network consists of interconnected processing elements called neurons that work together to produce an output function. The output of a neural network relies on the cooperation of the individual neurons within the network to operate. Well-designed neural networks are trainable systems that can often “learn” to solve complex problems from a set of examples and generalize the “acquired knowledge” to solve unforeseen problems, i.e., they are self-adaptive systems.
A neural network is used to refer to a network of biological neurons. A neural network consists of a set of highly interconnected entities called nodes or units. Each unit accepts a weighted set of inputs and responds with an output.
A neural network is first and foremost a graph, with patterns represented in terms of numerical values attached to the nodes of the graph and transformations between patterns achieved via simple message-passing algorithms. The graph contains a number of units and weighted unidirectional connections between them.
The output of one unit typically becomes an input for another. There may also be units with external inputs and outputs. The nodes in the graph are generally distinguished as being input nodes or output nodes and the graph as a whole can be viewed as a representation of a multivariate function linking inputs to outputs. Numerical values (weights) are attached to the links of the graphs, parameterizing the input/ output function and allowing it to be adjusted via a learning algorithm.
A broader view of a neural network architecture involves treating the network as a statistical processor characterized by making particular probabilistic assumptions about data. Figure illustrates one example of a possible neural network structure.
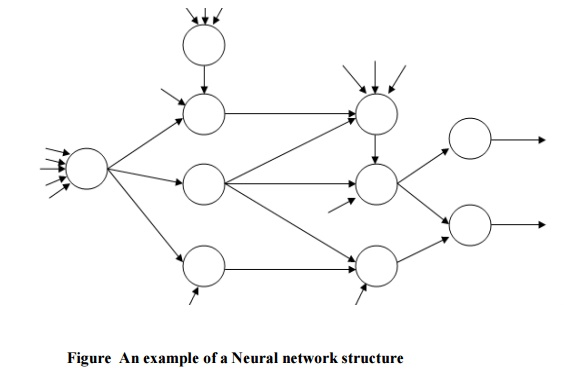
Fig 7: Example of neural net
Q11) Explain genetic algorithms?
A11) Genetic Algorithms
Genetic algorithms are based on the theory of natural selection and work on generating a set of random solutions and making them compete in an area where only the fittest survive. Each solution in the set is equivalent to a chromosome. Genetic algorithm learning methods are based on models of natural adaption and evolution. These learning methods improve their performance through processes which model population genetics and survival of the fittest.
In the field of genetics, a population is subjected to an environment which places demands on the members. The members which adapt well are selected for matting and reproduction. Generally genetic algorithms use three basic genetic operators like reproduction, crossover and mutation. These are combined together to evolve a new population. Starting from a random set of solutions the algorithm uses these operators and the fitness function to guide its search for the optimal solution.
The fitness function guesses how good the solution in question is and provides a measure to its capability. The genetic operators copy the mechanisms based on the principles of human evolution. The main advantage of the genetic algorithm formulation is that fairly accurate results may be obtained using a very simple algorithm.
The genetic algorithm is a method of finding a good answer to a problem, based on the feedback received from its repeated attempts at a solution. The fitness function is a judge of the GA’s attempts for a problem. GA is incapable to derive a problem’s solution, but they are capable to know from the fitness function.
The GA goes through the following cycle: Generate, Evaluate, Assignment of values, Mate and Mutate. One criteria is to let the GA run for a certain number of cycles. A second one is to allow the GA to run until a reasonable solution is found. Also, mutation is an operation, which is used to ensure that all locations of the rule space are reachable, that every potential rule in the rule space is available for evaluation. The mutation operator is typically used only infrequently to prevent random wandering in the search space.
Let us focus on the genetic algorithm as follows:
Step 1: Generate the initial population.
Step 2: Calculate the fitness function of each individual.
Step 3: Some sort of performance utility values or the fitness values are assigned to individuals.
Step 4: New populations are generated from the best individuals by the process of selection.
Step 5: Perform the crossover and mutation operation.
Step 6: Replace the old population with the new individuals.
Step 7: Perform step-2 until the goal is reached.
Q12) Describe an expert system?
A12) Expert Systems
The expert systems are the computer applications developed to solve complex problems in a particular domain, at the level of extra-ordinary human intelligence and expertise.
An expert system is a computer software that can handle complex issues and make decisions in the same way as a human expert can. It does so by pulling knowledge from its knowledge base based on the user's queries, employing reasoning and inference procedures.
An expert system's performance is determined on the knowledge stored in its knowledge base by the expert. The more knowledge that is stored in the KB, the better the system performs. When typing in the Google search box, one of the most common examples of an ES is a suggestion of spelling problems.
A computer simulation of a human expert is what an expert system is. It can also be defined as a computer program that mimics the judgment and behavior of a human or an organization with extensive knowledge and experience in a specific sector.
A knowledge base comprising acquired experience and a set of rules for applying the knowledge base to each specific circumstance given to the program are typically included in such a system. Human knowledge is also used by expert systems to address challenges that would ordinarily need human intelligence. Within the computer, these expert systems convey expertise knowledge as data or rules.
Knowledge Base
● It contains domain-specific and high-quality knowledge.
● Knowledge is required to exhibit intelligence. The success of any ES majorly depends upon the collection of highly accurate and precise knowledge
● The knowledgebase is a type of storage that stores knowledge acquired from the different experts of the particular domain. It is considered as big storage of knowledge. The more the knowledge base, the more precise will be the Expert System.
● It is similar to a database that contains information and rules of a particular domain or subject.
● One can also view the knowledge base as collections of objects and their attributes. Such as a Lion is an object and its attributes are it is a mammal, it is not a domestic animal, etc.
Components of Knowledge Base
● Factual Knowledge: The knowledge which is based on facts and accepted by knowledge engineers comes under factual knowledge.
● Heuristic Knowledge: This knowledge is based on practice, the ability to guess, evaluation, and experiences.
Knowledge Representation:
It is used to formalize the knowledge stored in the knowledge base using the If-else rules.
Q13) Write about an expert system shell?
A13) Expert system shell
An Expert system shell is a software development environment. It contains the basic components of expert systems. A shell is associated with a prescribed method for building applications by configuring and instantiating these components.
The generic components of a shell are shown below: information acquisition, knowledge Base, reasoning, explanation, and user interface. The key components are the knowledge base and reasoning engine.
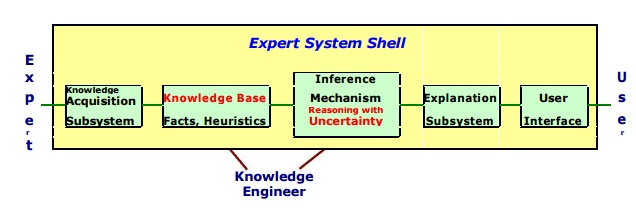
Fig 8: Expert system shell
● Knowledge Base – A database containing factual and heuristic information. One or more knowledge representation schemes are provided by the expert system tool for representing knowledge about the application domain. Frames (objects) and IF-THEN rules are both used by some tools. Knowledge is expressed in PROLOG as logical statements.
● Reasoning Engine – A path of reasoning in solving a problem is formed by inference processes for manipulating symbolic information and knowledge in the knowledge base. The inference mechanism can range from simple modus ponens backward chaining of IF-THEN rules to Case-Based reasoning.
● Knowledge Acquisition subsystem – A subsystem to help experts in build knowledge bases. However, collecting knowledge, needed to solve problems and build the knowledge base, is the biggest bottleneck in building expert systems.
● Explanation subsystem – A subsystem that explains the system's actions. The explanation can range from how the final or intermediate solutions arrived at justifying the need for additional data.
● User Interface – A means of communication with the user. The user interface is generally not a part of the expert system technology. It was not given much attention in the past. However, the user interface can make a critical difference in the user satisfaction of an Expert system.
Q14) What is knowledge Acquisition?
A14) Knowledge Acquisition
The gathering or collection of knowledge from multiple sources is known as knowledge acquisition. It is the process of adding new knowledge to a knowledge base while also refining or upgrading existing knowledge. The process of expanding a system's capabilities or improving its performance at a certain task is known as acquisition.
As a result, it is the production and refinement of knowledge with a specific objective in mind. Facts, rules, concepts, methods, heuristics, formulas, correlations, statistics, or any other relevant information can be found in acquired knowledge. Experts in the field, text books, technical papers, database reports, periodicals, and the environment are all possible sources of this knowledge.
Knowledge acquisition is an ongoing process that spans a person's entire life. Machine learning is an example of knowledge acquisition. It could be a process of self-learning or refinement with the help of computer programs. The newly learned knowledge should be meaningfully connected with existing knowledge.
The information should be accurate, non-redundant, consistent, and comprehensive. Knowledge acquisition aids activities such as knowledge entry and knowledge base maintenance. In order to refine current information, the knowledge acquisition process creates dynamic data structures.
The function of the knowledge engineer is equally critical in the development of knowledge refinements. Professionals who elicit knowledge from experts are known as knowledge engineers. They integrate knowledge from multiple sources through writing and editing code, operating numerous interactive tools, and creating a knowledge base, among other things.
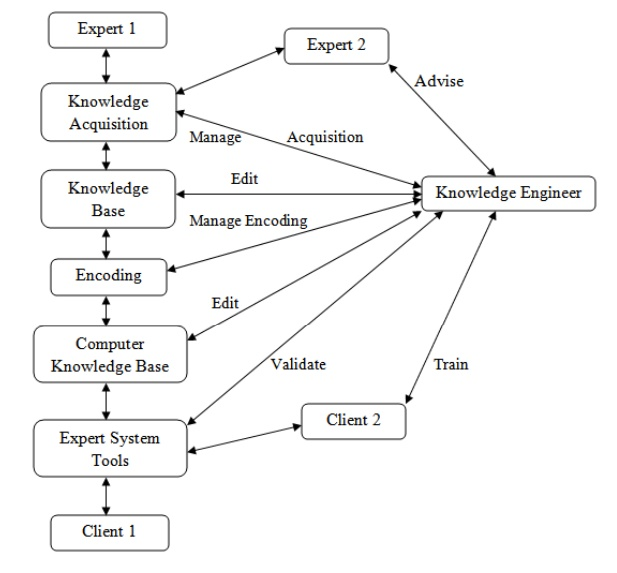
Fig 9: Knowledge Engineer’s Roles in Interactive Knowledge Acquisition