Unit – 3
Uncertainty
Q1) Explain uncertainty?
A1) Uncertainty
To act rationally in the face of uncertainty, we must be able to assess the likelihood of various events. A fact F is only useful in FOL if it is known whether it is true or untrue. However, we must be able to assess the likelihood that F is correct. We can construct methods for acting rationally under uncertainty by considering the likelihoods of events (probabilities).
Till now, we have learned knowledge representation using first-order logic and propositional logic with certainty, which means we were sure about the predicates. With this knowledge representation, we might write A→B, which means if A is true then B is true, but consider a situation where we are not sure about whether A is true or not then we cannot express this statement, this situation is called uncertainty.
To act sensibly in the face of uncertainty, we must be able to assess the likelihood of various events. A fact F is only useful in FOL if it is known whether it is true or untrue. However, we must be able to assess the likelihood that F is correct. We can construct methods for acting rationally under uncertainty by considering the likelihoods of events (probabilities).
Managing the uncertainty that is inherent in machine learning for predictive modeling can be achieved via the tools and techniques from probability, a field specifically designed to handle uncertainty.
So, to represent uncertain knowledge, where we are not sure about the predicates, we need uncertain reasoning or probabilistic reasoning.
Uncertainty is the biggest source of difficulty for beginners in machine learning, especially developers.
Noise in data, incomplete coverage of the domain, and imperfect models provide the three main sources of uncertainty in machine learning.
Probability provides the foundation and tools for quantifying, handling, and harnessing uncertainty in applied machine learning.
Q2) What is polish notations?
A2) Polish Notations
● Sample spaces S with events Ai, probabilities P(Ai); union A ∪ B and intersection AB, complement Ac.
● Axioms: P(A) ≤ 1; P(S) = 1; for exclusive Ai , P(∪iAi) = Σi P(Ai).
● Conditional probability: P(A|B) = P(AB)/P(B); P(A) = P(A|B)P(B) + P(A|Bc )P(Bc )
● Random variables (RVs) X; the cumulative distribution function (cdf) F(x) = P{X ≤ x};
for a discrete RV, probability mass function (pmf)
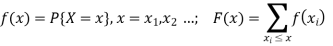
for a continuous RV, probability density function (pdf)
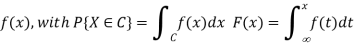
● Generalizations for more than one variable, e.g.
two RVs X and Y: joint cdf F (x, y) = P {X ≤ x, Y ≤ y};
pmf f (x, y) = P {X = x, Y = y}; or
pdf f (x, y), with
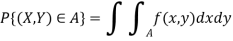
independent X and Y iff f (x, y) = fX(x) fY (y)
● Expected value or mean: for RV X, µ = E[X]; discrete RVs
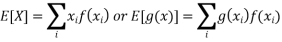
continuous RVs
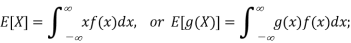
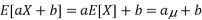
Q3) What do you mean by Axioms of Probability?
A3) Axioms of Probability
The formal procedures and rules for manipulating probabilistically expressed propositions are provided by Probability Theory. The three assumptions of probability theory are as follows:
● 0 <= P(A=a) <= 1 for all a in sample space of A
● P(True)=1, P(False)=0
● P(A v B) = P(A) + P(B) - P(A ^ B)
We can deduce the following properties from these axioms:
● P(~A) = 1 - P(A)
● P(A) = P(A ^ B) + P(A ^ ~B)
● Sum{P(A=a)} = 1, where the sum is over all possible values a in the sample space of A
Q4) Describe Full Joint Distributions Independence?
A4) Full Joint Distributions Independence
The influence of the parent on each node in the Bayesian network is determined by the condition probability distribution P(Xi |Parent(Xi)).
The Joint Probability Distribution and Conditional Probability are the foundations of the Bayesian network. So, first, let's look at the joint probability distribution:
If we have variables x1, x2, x3,....., xn, then the probabilities of a different combination of x1, x2, x3.. xn, are known as Joint probability distribution.
P[x1, x2, x3,....., xn], it can be written as the following way in terms of the joint probability distribution.
= P[x1| x2, x3,....., xn]P[x2, x3,....., xn]
= P[x1| x2, x3,....., xn]P[x2|x3,....., xn]....P[xn-1|xn]P[xn].
In general for each variable Xi, we can write the equation as:
P(Xi|Xi-1,........., X1) = P(Xi |Parents(Xi ))
We can completely specify all of the possible probabilistic information by constructing the full joint probability distribution, P(V1=v1, V2=v2,..., Vn=vn), which assigns probabilities to all possible combinations of values to all random variables, given an application domain in which we have determined a sufficient set of random variables to encode all of the relevant information about that domain.
Consider the domain Bird, Flier, and Young, which are described by three Boolean random variables. Then we may make a table with all of the possible interpretations and their probabilities:
Bird Flier Young Probability
T T T 0.0
T T F 0.2
T F T 0.04
T F F 0.01
F T T 0.01
F T F 0.01
F F T 0.23
F F F 0.5
The reason that the above table has 8 rows represents the fact that there are 23 different ways to assign values to the three Boolean variables. The table will be 2n in size if there are n Boolean variables. And if each of the n variables has k potential values, the table will be size kn.
Also, because we know the set of all possible values for each variable, the sum of the probabilities in the right column must equal 1. This indicates that the table has 2n -1 values that must be calculated for n Boolean random variables in order to entirely fill in the table.
We can compute any probabilistic statement about the domain if all of the probabilities for a full joint probability distribution table are known. We can compute, for example, using the table above.
● P(Bird=T) = P(B) = 0.0 + 0.2 + 0.04 + 0.01 = 0.25
● P(Bird=T, Flier=F) = P(B, ~F) = P(B, ~F, Y) + F(B, ~F, ~Y) = 0.04 + 0.01 = 0.05
Q5) Define Bayes’ Rule?
A5) Bayes’ Rule
Bayes' theorem, often known as Bayes' rule, Bayes' law, or Bayesian reasoning, is a mathematical formula for calculating the probability of an event based on ambiguous information.
It connects the conditional and marginal probabilities of two random events in probability theory.
Thomas Bayes, a British mathematician, provided the inspiration for Bayes' theorem. The Bayesian inference is a method of applying Bayes' theorem, which is central to Bayesian statistics.
It's a method for calculating the value of P(B|A) using P(A|B) knowledge.
By witnessing additional information from the real world, Bayes' theorem can update the probability forecast of an occurrence.
Example: If cancer is related to one's age, we can use Bayes' theorem to predict the likelihood of cancer more precisely using age.
The product rule and conditional probability of event A with known event B can be used to derive Bayes' theorem:
As a result of the product rule, we can write:
P(A ⋀ B)= P(A|B) P(B) or
In the same way, the likelihood of event B if event A is known is:
P(A ⋀ B)= P(B|A) P(A)
When we combine the right-hand sides of both equations, we get:
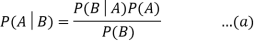
The above equation is known as Bayes' rule or Bayes' theorem (a). This equation is the starting point for most current AI systems for probabilistic inference.
It displays the simple relationship between joint and conditional probabilities. Here,
P(A|B) is the posterior, which we must compute, and it stands for Probability of hypothesis A when evidence B is present.
The likelihood is defined as P(B|A), in which the probability of evidence is computed after assuming that the hypothesis is valid.
Prior probability, or the likelihood of a hypothesis before taking into account the evidence, is denoted by P(A).
Marginal probability, or the likelihood of a single piece of evidence, is denoted by P(B).
In general, we can write P (B) = P(A)*P(B|Ai) in the equation (a), therefore the Bayes' rule can be expressed as:
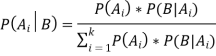
Where A1, A2, A3,..... is a set of mutually exclusive and exhaustive events, and An is a set of mutually exclusive and exha
Q6) What is Probabilistic Reasoning?
A6) Probabilistic Reasoning
Causes of uncertainty:
The following are some of the most common sources of uncertainty in the actual world.
● Information occurred from unreliable sources.
● Experimental Errors
● Equipment fault
● Temperature variation
● Climate change.
Probabilistic reasoning is a method of knowledge representation in which the concept of probability is used to convey the uncertainty in knowledge. To deal with uncertainty, we use probabilistic reasoning, which combines probability theory and logic.
Probability is used in probabilistic reasoning because it allows us to deal with the uncertainty that arises from someone's laziness or ignorance.
There are many scenarios in the actual world where something is not guaranteed, such as "it will rain today," "conduct of someone in particular settings," and "a contest between two teams or two players." These are probable sentences for which we can assume that it will happen but are not sure about it, so here we use probabilistic reasoning.
Probability: A probability that an uncertain occurrence will occur is defined as probability. It is a numerical representation of the probability of an event occurring. The probability value is always between 0 and 1, which represents perfect uncertainty.
0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.
P(A) = 0, indicates total uncertainty in an event A.
P(A) =1, indicates total certainty in an event A.
Using the formula below, we can calculate the likelihood of an uncertain event.
P(¬A) = probability of a not happening event.
P(¬A) + P(A) = 1.
Event: Each possible outcome of a variable is called an event.
Sample space: The collection of all possible events is called sample space.
Random variables: Random variables are used to represent the events and objects in the real world.
Prior probability: The prior probability of an event is probability computed before observing new information.
Posterior Probability: The probability that is calculated after all evidence or information has been taken into account. It is a combination of prior probability and new information.
Conditional probability: Conditional probability is a probability of occurring an event when another event has already happened.
Q7) What is the Semantics of Bayesian Networks?
A7) The Semantics of Bayesian Networks
● Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets, are a data structure for capturing all of the information in the whole joint probability distribution for the collection of random variables that define a domain. That is, every value in the whole joint probability distribution of the collection of random variables can be computed using the Bayesian Net.
● All direct causal links between variables are represented by this variable.
● Draw arcs from cause variables to immediate effects to build a Bayesian net for a given collection of variables.
● It saves space because it takes use of the fact that in many real-world problem domains, variable dependencies are often local, resulting in a large number of conditionally independent variables.
● The relationship between variables is captured in both qualitative and quantitative terms.
● Can be used to make a case
● Predictive reasoning (also known as causal reasoning) is a type of thinking that works from the top down (from causes to effects).
● Diagnostic reasoning works backwards (bottom-up) from effects to causes.
● A Bayesian Net is a directed, acyclic graph (DAG) in which each random variable has its own node and a directed arc from A to B whenever A has a direct causal influence on B. As a result, the nodes reflect states of affairs and the arcs represent direct causal linkages. The presence of A encourages the occurrence of B, and vice versa. Due to the existence of B, the backward influence is referred to as "diagnostic" or "evidential" support for A.
● Given the parents of A, each node A in a net is conditionally independent of any subset of nodes that are not offspring of A.
An Influence diagram is a generalized type of Bayesian network that illustrates and solves decision problems under uncertain knowledge.
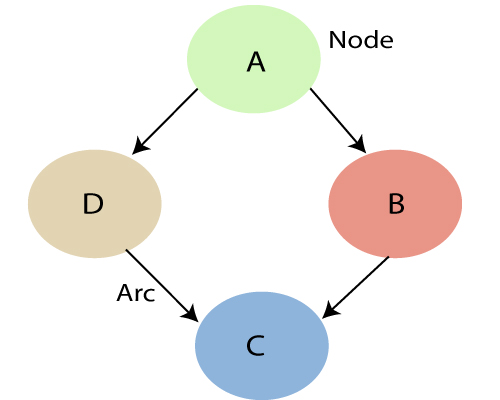
Fig 1: Bayesian network graph
● Each node represents a random variable, which can be either continuous or discontinuous.
● The causal relationship or conditional probabilities between random variables are represented by arcs or directed arrows. These directed links, also known as arrows, connect the graph's two nodes.
These ties indicate that one node has a direct influence on the other, and if there are no directed links, nodes are independent of one another.
Q8) Explain conditional probability?
A8) Conditional Probability
● Conditional probabilities are key for reasoning because they formalize the process of accumulating evidence and updating probabilities based on new evidence.
● For example, if we know there is a 4% chance of a person having a cavity, we can represent this as the prior (aka unconditional) probability P(Cavity)=0.04.
● Say that person now has a symptom of a toothache, we'd like to know what is the posterior probability of a Cavity given this new evidence. That is, compute P(Cavity | Toothache).
● If P(A|B) = 1, this is equivalent to the sentence in Propositional Logic B => A. Similarly, if P(A|B) =0.9, then this is like saying B => A with 90% certainty.
● In other words, we've made implication fuzzy because it's not absolutely certain.
● Given several measurements and other "evidence", E1, ..., Ek, we will formulate queries as P(Q | E1, E2, ..., Ek) meaning "what is the degree of belief that Q is true given that we know E1, ..., Ek and nothing else."
Conditional probability is defined as: P(A|B) = P(A ^ B)/P(B) = P(A,B)/P(B)
One way of looking at this definition is as a normalized (using P(B)) joint probability (P(A,B)).
● Example Computing Conditional Probability from the Joint Probability Distribution Say we want to compute P(~Bird | Flier) and we know the full joint probability distribution function given above.
● We can do this as follows:
● P(~B|F) = P(~B,F) / P(F)
= (P(~B,F,Y) + P(~B,F,~Y)) / P(F)
= (.01 + .01)/P(F)
Next, we could either compute the marginal probability P(F) from the full joint probability distribution, or, as is more commonly done, we could do it by using a process called normalization, which first requires computing
P(B|F) = P(B,F) / P(F)
= (P(B,F,Y) + P(B,F,~Y)) / P(F)
= (0.0 + 0.2)/P(F)
Now we also know that P(~B|F) + P(B|F) = 1, so substituting from above and solving for P(F) we get P(F) = 0.22. Hence, P(~B|F) = 0.02/0.22 = 0.091.
While this is an effective procedure for computing conditional probabilities, it is intractable in general because it means that we must compute and store the full joint probability distribution table, which is exponential in size.
Some important rules related to conditional probability are:
● Rewriting the definition of conditional probability, we get the Product Rule: P(A,B) = P(A|B)P(B)
● Chain Rule: P(A,B,C,D) = P(A|B,C,D)P(B|C,D)P(C|D)P(D), which generalizes the product rule for a joint probability of an arbitrary number of variables. Note that ordering the variables results in a different expression, but all have the same resulting value.
● Conditionalized version of the Chain Rule: P(A,B|C) = P(A|B,C)P(B|C)
● Bayes's Rule: P(A|B) = (P(A)P(B|A))/P(B), which can be written as follows to more clearly emphasize the "updating" aspect of the rule: P(A|B) = P(A) * [P(B|A)/P(B)] Note: The terms P(A) and P(B) are called the prior (or marginal) probabilities. The term P(A|B) is called the posterior probability because it is derived from or depends on the value of B.
● Conditionalized version of Bayes's Rule: P(A|B,C) = P(B|A,C)P(A|C)/P(B|C)
● Conditioning (aka Addition) Rule: P(A) = Sum{P(A|B=b)P(B=b)} where the sum is over all possible values b in the sample space of B.
● P(~B|A) = 1 - P(B|A)
● Assuming conditional independence of B and C given A, we can simplify Bayes's Rule for two pieces of evidence B and C:
P(A | B,C) = (P(A)P(B,C | A))/P(B,C)
= (P(A)P(B|A)P(C|A))/(P(B)P(C|B))
= P(A) * [P(B|A)/P(B)] * [P(C|A)/P(C|B)]
= (P(A) * P(B|A) * P(C|A))/P(B,C)
Q9) Write is Exact Inference in Bayesian Networks?
A9) Exact Inference in Bayesian Networks
● size of the graph).
● For singly-connected networks or polytrees in which there are no undirected loops, there are linear time algorithms based on belief propagation.
● Each node sends local evidence messages to their children and parents.
● Each node updates belief in each of its possible values based on incoming messages from it neighbors and propagates evidence on to its neighbors.
● There are approximations to inference for general networks based on loopy belief propagation that iteratively refines probabilities that converge to an accurate limit.
Temporal model
Q10) What is Approximate Inference in Bayesian Networks?
A10) Approximate Inference in Bayesian Networks
Direct sampling method
For Bayesian networks, the most basic type of random sampling procedure generates events from a network with no evidence connected with them. The concept is to sample each variable in topological order. The value is sampled from a probability distribution that is conditioned on the values already assigned to the variable's parents.
function PRIOR-SAMPLE(bn) returns an event sampled from the prior specified by bn
inputs: bn, a Bayesian network specifying joint distribution 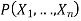
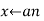 event with n elements
event with n elements
foreach variable 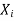 in
in 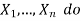
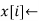 a random sample from P(
a random sample from P(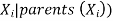
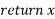
Likelihood weighting
Likelihood weighting eliminates the inefficiencies of rejection sampling by creating only events that are consistent with the evidence. It's a tailored version of the general statistical approach of importance sampling for Bayesian network inference.
Function LIKELIHOOD-WEIGHTING (X, e, bn, N) returns an estimate of 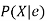
Inputs: X, the query variable
e, observed values for variables E
bn, a Bayesian network specifying joint distribution 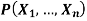
N, the total number of samples to be generated
Local variables: W, a vector of weighted counts for each value of X, initially zero
For j=1 to N do
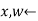 WEIGHTED-SAMPLE(bn,e)
WEIGHTED-SAMPLE(bn,e)
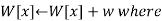 x is the value of X in x
x is the value of X in x
 NORMALIZE (W)
NORMALIZE (W)
Inference by Markov chain simulation
Markov chain (MCMC) MARKOV CHAIN methods are not the same as rejection sampling and likelihood weighting. MCMC methods produce each sample by applying a random change to the previous sample, rather than starting from scratch. It's easier to think of an MCMC algorithm as being in a current state where each variable has a value and then generating a new state by making random modifications to the existing state.