Unit – 1
Introduction
Q1) What is artificial intelligence?
A1) Artificial Intelligence
Artificial Intelligence (AI) is an area of science that focuses on assisting robots in discovering human-like answers to hard problems. This usually entails taking traits from human intelligence and converting them into computer-friendly algorithms. Depending on the requirements, a more or less flexible or efficient strategy might be used, which determines how artificial the intelligent behavior seems.
Although AI is most commonly linked with computer science, it has numerous crucial connections with other disciplines such as mathematics, psychology, cognition, biology, and philosophy, to name a few. Our ability to combine knowledge from all these fields will ultimately benefit our progress in the quest of creating an intelligent artificial being.
AI now spans a wide range of subfields, ranging from general-purpose areas like perception and logical reasoning to specific jobs like chess, mathematical theorems, poetry creation, and disease diagnosis.
Q2) what do you mean by agent and environments?
A2) Agents and Environments
An agent and its environment make up an AI system. The agents interact with their surroundings. Other agents may be present in the environment.
An agent is anything with sensors that can sense its environment and effectors that can act on that environment.
● Human agents: such as the eyes, ears, nose, tongue, and skin are parallel to the sensors, and effector organs such as the hands, legs, and mouth are parallel to the effectors.
● Robotics agents: For sensors, a robotic agent replaces cameras and infrared range finders, and for effectors, various motors and actuators.
● Software agents: The programs and activities of a software agent are encoded bit strings.
Sensor: A sensor is an electronic device that detects changes in the environment and transmits the data to other electronic devices. Sensors allow an agent to observe its surroundings.
Actuator: Actuators are machines' components that turn energy into motion. The actuators' sole function is to move and control a system. An actuator can be anything from an electric motor to gears to rails.
Effectors: Effectors are devices that have an impact on the environment. Legs, wheels, arms, fingers, wings, fins, and a display screen are examples of effectors.
An agent's environment is everything in the world that surrounds him or her, but it is not a part of him or her. A context in which an agent is present is referred to as an environment.
The agent's environment is where he or she lives, works, and has something to detect and react to. The majority of the time, an environment is described as non-feministic.
Q3) Define Rationality?
A3) Rationality
Rationality is nothing but the status of being rational, sensible, and having a good sense of judgment.
Rationality is concerned with the predicted actions and outcomes based on the agent's perceptions. An important aspect of rationality is taking activities with the goal of getting meaningful information.
The performance metric of an agent is used to determine its rationality. The following criteria can be used to assess rationality:
● The success criterion is defined by a performance metric.
● The agent has prior knowledge of its surroundings.
● The most effective activities that an agent can take.
● The order in which percepts appear.
Q4) Write about Nature of Environments?
A4) Nature of Environments
Some programs work in a completely artificial world, with just keyboard input, databases, computer file systems, and character output on a screen.
Some software agents (software robots or softbots) exist in rich, limitless softbots domains, on the other hand. The environment in the simulator is extremely detailed and complicated. In real time, the software agent must choose from a large number of options. A softbot that scans a customer's internet preferences and displays intriguing goods to them operates in both a real and an artificial environment.
The Turing Test environment is the most well-known artificial setting, in which one real and other artificial agents are tested on an equal footing. This is a difficult setting to work in because a software agent can't perform as well as a human.
Turing test
The Turing Test can be used to assess the success of a system's intelligent behavior.
The test involves two people and a machine that will be examined. One of the two people takes on the job of a tester. They are all in different rooms. The tester has no idea who is a human and who is a machine. He types the queries and sends them to both intelligences, who respond to him with typed responses.
This test aims at fooling the tester. If the tester fails to determine the machine's response from the human response, then the machine is said to be intelligent.
Q5) Explain Solving problems by search?
A5) SOLVING PROBLEMS BY SEARCH
Search techniques are universal problem-solving strategies in Artificial Intelligence. These search strategies or algorithms were generally employed by rational agents or problem-solving agents in AI to solve a given problem and deliver the best outcome. Goal-based agents that use atomic representation are problem-solving agents. We will learn a variety of problem-solving search methods in this area.
Searching Algorithms Terminologies:
● Search: Searching is a step-by-step process for resolving a search problem in a certain search space. There are three basic variables that can contribute to a search problem:
○ Search space: A search space is a collection of probable solutions that a system could have.
○ Start state: It's the starting point for the agent's quest.
○ Goal test: It's a function that looks at the current state and returns whether or not the goal state has been reached.
● Search tree: Search tree is a tree representation of a search problem. The root node, which corresponds to the initial state, is at the top of the search tree.
● Actions: It provides the agent with a list of all available actions.
● Transition model: A transition model is a description of what each action does.
● Path cost: It's a function that gives each path a numerical cost.
● Solutions: It is an action sequence that connects the start and end nodes.
● Optimal solutions: If a solution is the cheapest of all the options.
Q6) What do you mean by Formulating problems?
A6) Formulating problems
The problem of traveling to Bucharest was previously formulated in terms of the beginning state, activities, transition model, goal test, and path cost. Although this formulation appears to be fair, it is still a model—an abstract mathematical description—rather than the real thing.
Compare the simple state description we chose, In(Arad), to a cross-country trip, where the state of the world encompasses a wide range of factors, including the traveling companions, what's on the radio, the scenery out the window, whether there are any law enforcement officers nearby, how far it is to the next rest stop, the road condition, the weather, and so on.
All of these factors are absent from our state descriptions since they are unrelated to the task of locating a route to Bucharest. Abstraction is the process of removing details from a representation.
We must abstract both the state description and the actions themselves in addition to the state description. A driving action has a variety of outcomes. It takes time, uses fuel, produces pollutants, and changes the agent, in addition to changing the position of the vehicle and its occupants (as they say, travel is broadening). Only the change in location is taken into consideration in our algorithm.
Can we be more specific about what level of abstraction is appropriate? Consider the abstract states and actions we've chosen to be vast collections of detailed world states and action sequences. Consider a path from Arad to Sibiu to Rimnicu Vilcea to Pitesti to Bucharest as an example of a solution to the abstract problem. A wide number of more detailed paths correlate to this abstract solution.
Q7) Describe Searching for a solution?
A7) Searching for solution
We now need to solve the challenges we've formulated. Because a solution is a series of actions, search algorithms explore a variety of alternative action sequences. Starting with the initial state, the SEARCH TREE potential action sequences create a search tree with the initial state NODE at the root; the branches are actions, and the nodes correspond to states in the problem's state space.
The initial few steps in constructing the search tree for discovering a route from Arad to Bucharest are shown in Figure. The starting state is represented by the root node of the tree (Arad). The first step is to see if this is a goal state or not. (Obviously, it isn't, but it's worth double-checking so we can solve tricky issues like "beginning in Arad, get to Arad.") Then we must consider a variety of options. This is accomplished by extending the present state; that is, each legal action is applied to the existing state, resulting in the creation of a new set of states. In this scenario, we create three additional child nodes from the parent node In(Arad): In(Sibiu), In(Timisoara), and In(Sibiu) (Zerind).
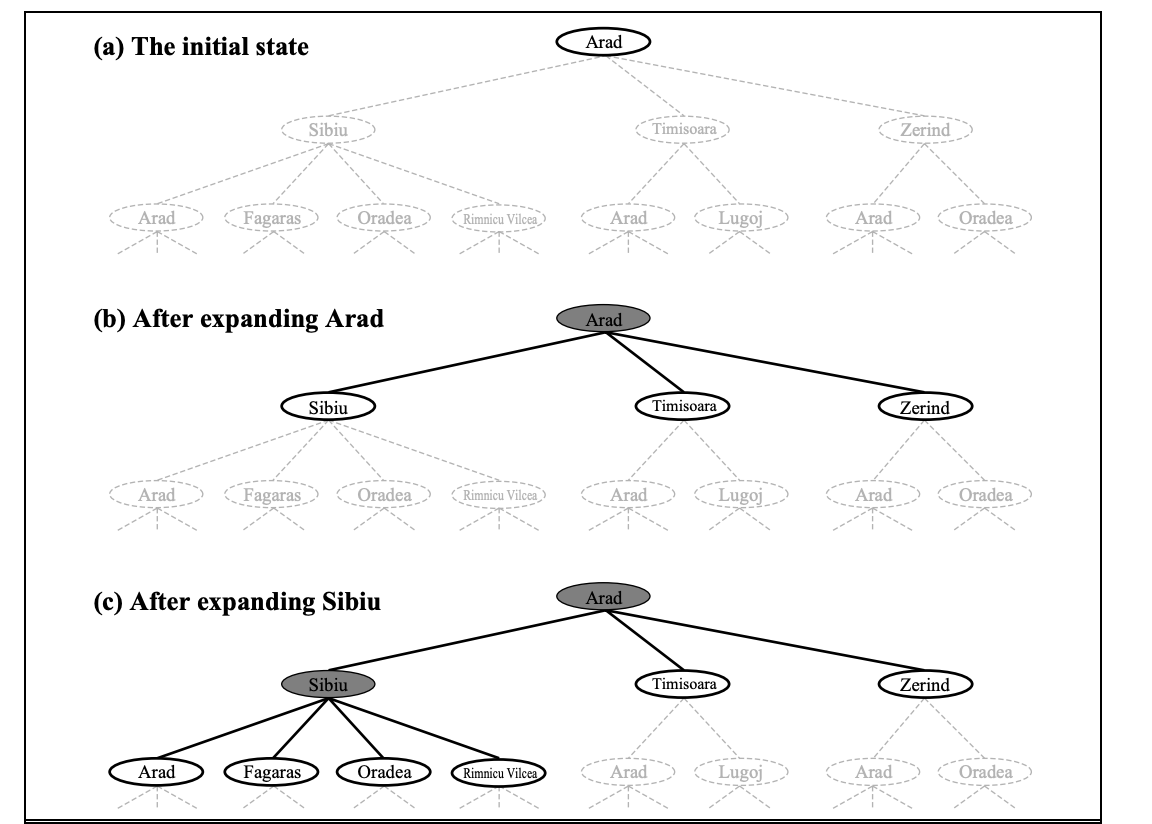
Fig 1: Partial search tree
This is the core of searching: pursuing one alternative at a time while putting the others on hold in case the first does not lead to a solution. Let's say we start with Sibiu. We check if it's a target state (it isn't), then expand it to get In(Arad), In(Fagaras), In(Oradea), and In(Oradea) (RimnicuVilcea). We may then select one of these four options, or we may return to LEAF NODE and select Timisoara or Zerind. Each of these six nodes is a leaf node in the tree, meaning it has no offspring.
The frontier is the collection of all leaf nodes that are accessible for expansion at any particular FRONTIER point. In Figure, the frontier of each tree consists of those nodes with bold outlines.
The process of selecting and expanding nodes on the frontier continues until a solution is found or no more states can be expanded. Figure depicts the overall TREE-SEARCH algorithm informally. The underlying foundation of all search algorithms is the same; the difference is in how they choose which state to expand next—the so-called search strategy.
function TREE-SEARCH (problem) returns a solution, or failure
initialize the frontier using the initial state of problem
loop do
if the frontier is empty then return failure
choose a leaf node and remove it from the frontier
if the node contains a goal state then return the corresponding solution
expand the chosen node, adding the resulting nodes to the frontier
function GRAPH-SEARCH(problem) returns a solution, or failure
initialize the explored set to be empty
loop do
if the frontier is empty then return failure
choose a leaf node and remove it from the frontier
if the node contains a goal state then return the corresponding solution
add the node to the explored set
expand the chosen node, adding the resulting nodes to frontier
only if not in the frontier or explored set
Fig 2: An informal description of the general tree-search and graph-search algorithms.
Q8) Explain Breadth-first search?
A8) Breadth-first search
A general strategy for traversing a graph is breadth first search. Although a breadth first search consumes more memory, it always finds the shortest path first. The state space is represented as a tree in this style of search. The solution can be found by traversing the tree. The start value or starting state, numerous intermediate states, and the end state are represented by the tree's nodes.
A queue data structure is employed in this search, and it is traversed level by level. Nodes are expanded in order of their distance from the root in a breadth-first search. It's a path-finding algorithm that can always discover a solution if one is available. The solution which is found is always the optional solution. This task is completed in a very memory intensive manner. Each node in the search tree is expanded breadth wise at each level.
Algorithm:
Step 1: Place the root node inside the queue.
Step 2: If the queue is empty then stops and returns failure.
Step 3: If the FRONT node of the queue is a goal node then stop and return success. Step 4: Remove the FRONT node from the queue. Process it and find all its neighbours that are in a ready state then place them inside the queue in any order.
Step 5: Go to Step 3.
Step 6: Exit.
Implementations
Let us implement the above algorithm of BFS by taking the following suitable example
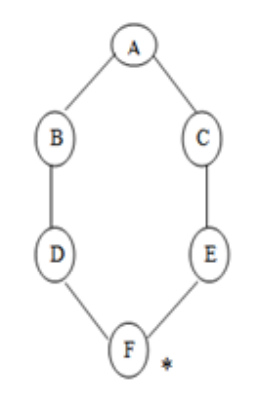
Fig 3: Example
Consider the graph below, where A is the initial node and F is the destination node (*).
Step 1: Place the root node inside the queue i.e. A
Step 2: The queue is no longer empty, and the FRONT node, i.e. A, is no longer our goal node. So, proceed to step three.
Step 3: Remove the FRONT node, A, from the queue and look for A's neighbors, B and C.
Step 4: Now, b is the queue's FRONT node. As a result, process B and look for B's neighbors, i.e., D.
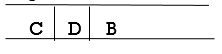
Step 5: Find out who C's neighbors are, which is E.

Ste 6: As D is the queue's FRONT node, find out who D's neighbors are.
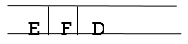
Step 7: E is now the queue's first node. As a result, E's neighbor is F, which is our objective node.
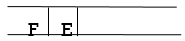
Step 8: Finally, F is the FRONT of the queue, which is our goal node. As a result, leave.
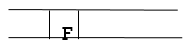
Q9) Write advantages and disadvantages of BFS?
A9) Advantages
● In this technique, the aim will be reached in whatever way.
● For a long period, it does not choose any unproductive paths.
● In the case of many paths, it finds the simplest solution.
Disadvantages
● BFS takes up a lot of memory.
● It has a higher time complexity.
● When all paths to a destination have almost the same search depth, it has long pathways.
Q10) Describe Depth-first search?
A10) Depth-first search
DFS is a type of uniform search that is also very essential. DFS traverses the graph's vertices. This type of algorithm will always select to explore the graph further. DFS selects one of the remaining undiscovered vertices and continues the search after visiting all the reachable vertices from a particular source.
DFS always generates a child of the deepest unexpanded nodded, which serves as a reminder of the space constraint of breath first search. DFS employs the data structure stack, often known as last in first out (LIFO). The discover and finish time of each vertex from a parenthesis structure is a noteworthy property of DFS.
Algorithm:
Step 1: PUSH the starting node into the stack.
Step 2: If the stack is empty then stop and return failure.
Step 3: If the top node of the stack is the goal node, then stop and return success. Step 4: Else POP the top node from the stack and process it. Find all its neighbours that are in ready state and PUSH them into the stack in any order.
Step 5: Go to step 3.
Step 6: Exit.
Implementation:
Let us take an example for implementing the above DFS algorithm.
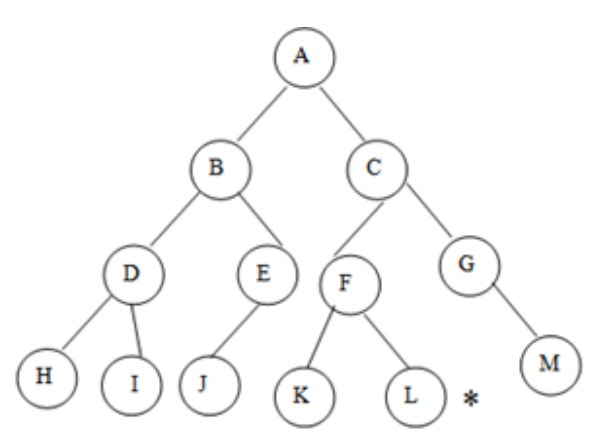
Fig 4: Example
In the graph, A represents the root node and L represents the goal node.
Step 1: PUSH the stack's initial node, i.e.

Step 2: The stack is no longer empty, and A is no longer our objective node. As a result, go to the next step.
Step 3: POP the top node from the stack, A, and look for A's neighbors, B and C.

Step 4: C is now the stack's top node. Look for its neighbors, F and G.
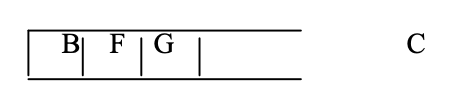
Step 5: G is now the stack's top node. Find its next-door neighbor, M.
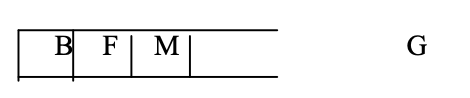
Step 6: Now that M is the top node, identify its neighbor. However, since M has no neighbors in the graph, POP it from the stack.

Step 7: Now that F is the top node, and K and L are its neighbors, PUSH them onto the stack.
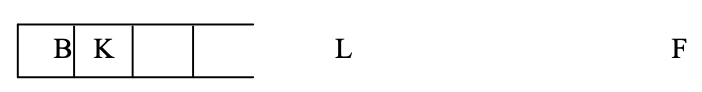
Step 8: L is now the stack's top node, which is also our goal node.

You can also traverse the graph starting at the root A and inserting C and B onto the stack in that order.
Q11) Write pros and cons of DFS?
A11) Pros
● DFS uses a small amount of memory.
● If it follows the correct path, it will arrive at the goal node in less time than BFS.
● It may locate a solution without having to look through a lot of results because we may receive the desired result right away.
Cons
● It's possible that some states will recur.
● There is no certainty that the goal node will be found.
● In some cases, the states may become stuck in an unending loop.
Q12) Describe Informed (Heuristic) Search Strategies?
A12) Informed (Heuristic) Search Strategies
A heuristic is a technique that improves the efficiency of our search method. Some heuristics aid in the direction of a search process without abandoning any claim to completeness, whereas others do so. A heuristic is a piece of problem-specific knowledge that reduces the amount of time spent searching. It's an approach that works occasionally but not always.
The knowledge about the problem is used by the heuristic search algorithm to assist lead the path across the search space. These searches make use of several functions that estimate the cost of getting from where you are now to where you want to go, assuming that the function is efficient.
A heuristic function is a function that maps from problem state descriptions to measure of desirability usually represented as numbers. The purpose of heuristic function is to guide the search process in the most profitable directions by suggesting which path to follow first when more than is available.
For finding a solution, by using the heuristic technique, one should carry out the following steps:
1. Add domain—specific information to select what is the best path to continue searching along.
2. Define a heuristic function h(n) that estimates the ‘goodness’ of a node n. Specifically, h(n) = estimated cost(or distance) of minimal cost path from n to a goal state.
3. The term heuristic means ‘serving to aid discovery’ and is an estimate, based on domain specific information that is computable from the current state description of how close we are to a goal.
Finding a route from one city to another city is an example of a search problem in which different search orders and the use of heuristic knowledge are easily understood.
1. State: The current city in which the traveller is located.
2. Operators: Roads linking the current city to other cities.
3. Cost Metric: The cost of taking a given road between cities.
4. Heuristic information: The search could be guided by the direction of the goal city from the current city, or we could use airline distance as an estimate of the distance to the goal.
Q13) Explain Greedy best-first search?
A13) Greedy best-first search
This method has a strategy that is quite similar to that of the best first search algorithm. It's a straightforward best-first search that lowers the anticipated cost of achieving the goal. Essentially, it selects the node that looks to be closest to the target. This search begins with the initial matrix and makes all conceivable adjustments before examining the change in the score. The tweak is then applied until the maximum improvement is found. The search will continue until there are no more improvements to be made. A lateral move is never made by the greedy search.
It uses minimal estimated cost h (n) to the goal state as a measure which decreases the search time but the algorithm is neither complete nor optimal. The main advantage of this search is that it is simple and finds solutions quickly. The disadvantages are that it is not optimal, susceptible to false start.
Fig 5: Greedy search
A graph search algorithm in which a node is chosen for expansion based on an evaluation function f is known as the best first search (n). Because the assessment gauges distance to the goal, the node with the lowest assessment is traditionally chosen for the explanation. A priority queue, a data structure that keeps the fringe in ascending order of f values, can be used to achieve best first search within a general search framework. The depth first and breadth first search algorithms are combined in this search algorithm.
Algorithm:
Step 1: Place the starting node or root node into the queue.
Step 2: If the queue is empty, then stop and return failure.
Step 3: If the first element of the queue is our goal node, then stop and return success.
Step 4: Else, remove the first element from the queue. Expand it and compute the estimated goal distance for each child. Place the children in the queue in ascending order to the goal distance.
Step 5: Go to step-3.
Step 6: Exit
Q14) What is A* Search?
A14) A* Search
Since its creation in 1968 by Peter Hart, Nils Nilsson, and Bertram Raphael, A* has been a common term for several AI systems. It's a hybrid of Dijkstra's algorithm with the Best First Search method. It may be used to solve a wide range of issues. Using a heuristic function, A* search seeks the shortest path through a search space to the objective state.
This method seeks out low-cost solutions and leads to a goal state known as A* search. The * in A* is written for the sake of optimality. The A* the algorithm also determines the least expensive path between the start and target states, when switching from one state to another incurs a cost.
A* requires heuristic function to evaluate the cost of path that passes through the particular state. This algorithm is complete if the branching factor is finite and every action has a fixed cost. A* requires heuristic function to evaluate the cost of path that passes through the particular state. It can be defined by the following formula.
F (n) = g (n) + h (n)
Where
g (n): The actual cost path from the start state to the current state.
h (n): The actual cost path from the current state to the goal state.
f (n): The actual cost path from the start state to the goal state. For the implementation of A* algorithm we will use two arrays namely OPEN and CLOSE.
OPEN: An array which contains the nodes that has been generated but has not been yet examined.
CLOSE: An array which contains the nodes that have been examined.
Algorithm:
Step 1: Place the starting node into OPEN and find its f (n) value.
Step 2: Remove the node from OPEN, having the smallest f (n) value. If it is a goal node then stop and return success.
Step 3: Else remove the node from OPEN, find all its successors.
Step 4: Find the f (n) value of all successors; place them into OPEN and place the removed node into CLOSE.
Step 5: Go to Step-2.
Step 6: Exit.
Q15) Write advantages and disadvantages of A* search?
A15) Advantages
● It is complete and optimal.
● It is the best one from other ways.
● It's utilized to solve really difficult tasks.
● It is the most efficient method, in the sense that no other method is guaranteed to expand fewer nodes than A*.
Disadvantages
● If the branching factor is finite and every action has a fixed cost, this method is complete.
● The accuracy of the heuristic approach used to compute h determines how quickly A* search may be completed (n).
● It has issues with complexity.
Q16) Write short notes on CSP?
A16) CSP
A constraint satisfaction problem (CSP) consists of
The aim is to choose a value for each variable so that the resulting possible world satisfies the constraints; we want a model of the constraints.
CSPs are mathematical puzzles in which the state of a group of objects must meet a set of constraints.
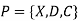
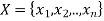
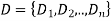
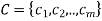
A CSP over finite domains is depicted in the diagram. We have a collection of variables (X), a set of domains (D), and a set of constraints (C) to work with.
The values assigned to variables in X must fall into one of D's domains.
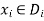
A constraint restricts the possible values of a subset of variables from X.
A finite CSP has a finite number of variables and each variable has a finite domain. Although several of the approaches discussed in this chapter are designed for infinite, even continuous domains, many of them only operate for finite CSPs.
Given a CSP, there are a number of tasks that can be performed:
Q17) What do you mean by means-end analysis?
A17) Mean - End - Analysis
Most search strategies work in one of two directions: forward or backward. However, a combination of the two is frequently necessary. Solving the big portions of the problem first and then solving the lesser problems that arise when mixing them together would be doable with such a hybrid strategy. "Means - Ends Analysis" is one such methodology.
The purpose of the means-ends analysis is to determine the difference between the existing condition and the desired state. The means-ends analysis problem space has an initial state and one or more goal states, a set of operations with a set of preconditions for their application, and different functions that compute the difference between two states a(i) and s. (j). A problem is solved using means - ends analysis by
(the first AI program to use means - ends analysis was the GPS General problem solver)
means- ends analysis is useful for many human planning activities. Consider the example of planning for an office worker. Suppose we have a different table of three rules: