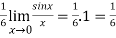Question Bank
Unit–4
Differential Calculus
Question-1: Verify Rolle’s theorem for the function f(x) = x(x+3)  in interval [-3 , 0].
in interval [-3 , 0].
Sol. First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x) 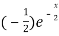 + (2x + 3)
+ (2x + 3)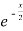
= 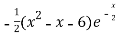
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
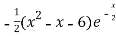 = 0
= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Question-2: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol. (1)
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+  and 2 -
and 2 - 
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Question-3: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) =  =
= 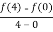 =
= 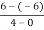 = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 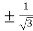
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Question-4: Expand the function 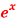 in ascending powers of (x – 1) by using Taylor’s theorem.
in ascending powers of (x – 1) by using Taylor’s theorem.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 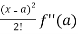 + ………
+ ……… . ………….(1)
. ………….(1)
Here f(x) =  and a = 1
and a = 1
Now,
f’(x) = 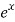 and f’(a) = e
and f’(a) = e
f’’(x) = 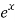 and f’’(a) = e
and f’’(a) = e
Put these values in equation (1),
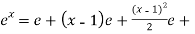 …………….
…………….
Take ‘e’ as common,
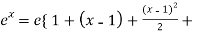 …………….}
…………….}
Which is the required expansion.
Question-5: Find the Taylor’s series for the function f(x) = 3x² - 6x + 5 in ascending powers of x-3.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 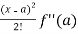 + ………
+ ……… . ………….(1)
. ………….(1)
Here ,
f(x) = 3x² - 6x + 5 and a = 3. So that f(a) = 14
Now , we will find out the derivatives ,
f’(x) = 6x – 6 and f’(3) = 12
f’’(x) = 6 and f’’(3) = 6
f’’’(x) = 0 and f’’’(x) = 14
Put these values in Taylor’s theorem, we get
3x² - 6x + 5 = 14 + 12(x-3) + 6 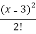 +…………. Ans.
+…………. Ans.
Question-6: Evaluate 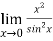 .
.
Sol. Let f(x) = 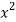 and g(x) =
and g(x) = 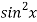 .
.
Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-
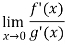
= 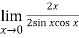
= 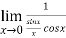
= 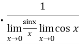 = 1
= 1
Question-7: Evaluate 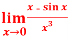
Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’Hospital’s rule, we get
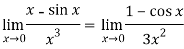
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-
We get
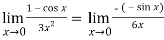 =
= 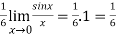
Question-8: Find 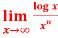 , n>0.
, n>0.
Sol. Let f(x) = log x and g(x) = 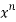
These two functions satisfied the theorem that we have discussed above-
So that,
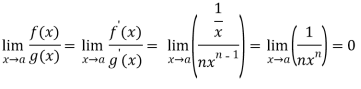
Question-9: Find out the maxima and minima of the function

Given 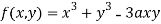 …(i)
…(i)
Partially differentiating (i) with respect to x we get
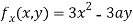 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
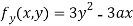 ….(iii)
….(iii)
Now, form the equations 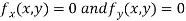
Using (ii) and (iii) we get
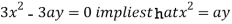
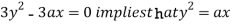
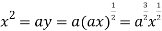 using above two equations
using above two equations
Squaring both side we get
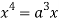
Or 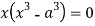
This show that 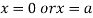
Also we get 
Thus we get the pair of value as 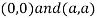
Now, we calculate
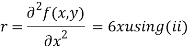
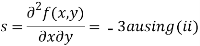
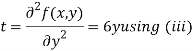
Putting above values in

At point (0,0) we get

So, the point (0,0) is a saddle point.
At point 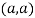 we get
we get
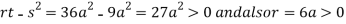
So the point 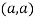 is the minimum point where
is the minimum point where 
In case 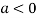
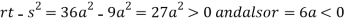
So the point 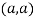 is the maximum point where
is the maximum point where 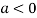
Question-10: Evaluate

Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’Hospital’s rule, we get

But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-
We get
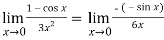 =
=