UNIT-7
Stability in the frequency domain
It gives the frequency response of the system. If the transfer function is given, then from the plot number of poles and zeros can be calculated.
Polar plot of some standard functions: -
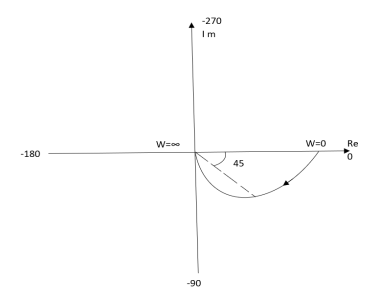
# TYPE ‘O’ Ex: 1T(S) = 1/S + 1 (1). For polar plot substitute S=jw. TF = 1/1 + jw (2). Magnitude M = 1 + 0j / 1 + jw = 1/√1 + w2 (3). Phase φ = tan-1(0)/ tan-1w = - tan-1w W M φ 0 1 00 1 0.707 -450 ∞ 0 -900 |
The plot is shown in fig. 1(a) |
|
Fig 1(a) Polar Plot T(S) = 1/S + 1
Ex.2>. T(S) = 1/(S+1) (S+2)
(1). S = jw
TF = 1/(1+jw) (2+jw)
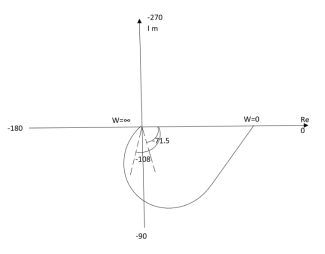
(2). M = 1/(1+jw) (2+jw) = 1/-w2 + 3jw + 2 M = 1/√1 + w2√4 + w2 (3). Φ = - tan-1 w - tan-1(w/2) W M Φ 0 0.5 00 1 0.316 -71.560 2 0.158 -108.430 ∞ 0 -1800
|
The plot is shown in fig2(b)
|
Fig 2(b) Polar Plot T(S) = 1/(S+1) (S+2)
Intersection of polar plot with imaginary axis will be when real part of Transfer function = 0
M = 1/ (jw + 1) (jw + 2)
= 1/-w2 + j3w + 2
TYPE ‘1’
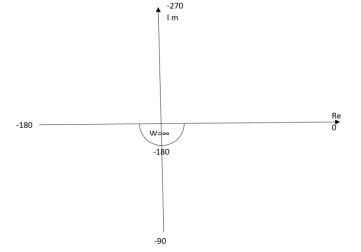
Ex.1 T(S) = 1/S
(1). S = jw
(2). M = 1/W
(3). Φ = -tan-1(W/O) = -900
W M φ
0 ∞ -900
1 1 -900
2 0.5 -900
∞ 0 -900
The plot is shown in fig.4(a)
|
Fig 4(a) Polar Plot T(S) = 1/S
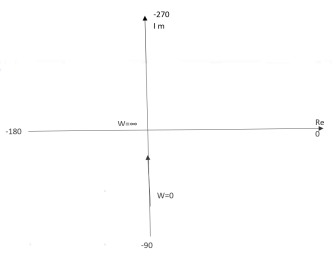
Ex.2 T(S) = 1/S2 (1). S = jw (2). M = 1/w2 (3). Φ = -tan-1(W/O)-tan-1(W/O) = -1800 W M Φ 0 ∞ -1800 1 1 -1800 2 0.25 -1800 ∞ 0 -1800
|
The plot is shown in fig.4(b)
|
Fig 4(b) Polar Plot T(S) = 1/S2
Key takeaways
- For Polar Plot starting point depends upon type of system
- The terminating phase depends on order of the system.
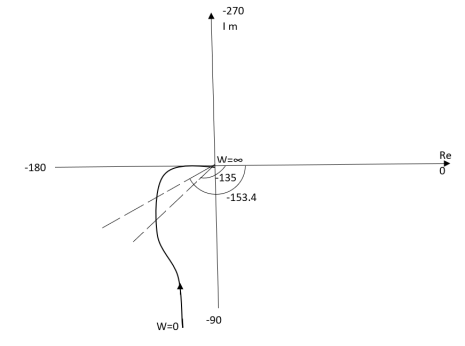
TYPE 1 ORDER 2
Ex.1 T(S) = 1/S(S+1)
(1). M = 1/W√1+w2
(2). Φ = -900 - tan -1(W/T)
W M φ
0 ∞ -900
1 0.707 -1350
2 0.45 -153.40
∞ 0 -1800
The plot is shown in fig.5(a)
|
Fig 5(a) Polar Plot T(S) = 1/S(S+1)
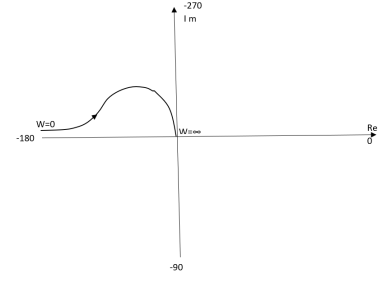
Ex.2TYPE 2 ORDER 3
T(s) = 1/S2(S+1)
(1). M = 1/w2√1+jw
(2). Φ = -1800 – tan-1W/T
The plot is shown in fig.5(b)
|
Fig 5(b) Polar Plot T(s) = 1/S2(S+1)
It gives the frequency response as well as comments on the stability and the relative stability of the system.
Nyquist Stability Criteria:
The Nyquist criteria is a semi graphical method that determines stability of CL system investigating the properties of the frequency domain plot (Polar plot), the Nyquist plot of the OLTF G(S) H(S) is represented as L(S)
L(S) = G(S)H(S)
Specially the Nyquist plot of L(S) is a plot drawn by substituting S=jw and varying the value of w as per in polar plot. In polar plot we take one sided frequency response (0 - ∞) in Nyquist plot we will vary the frequency in entire range possible from (-∞ to 0) and (0 to ∞)
Nyquist Criteria also gives: -
(1). In addition to providing the absolute stability like other plots, the Nyquist criteria also gives information on the relative stability of a stable system and the degree of instability of an unstable system.
(2). It also gives indications on how the system stability can be improved.
(3). The Nyquist plot of G(S) H(S) is the polar plot of G(S) H(S) drawn with wider range of frequency (-∞ to ∞) and along the Nyquist path.
(4). The Nyquist plot of G(S) H(S) gives information on frequency domain characteristics such as B.W, gain margin and phase margin.
Construction of Nyquist Plot
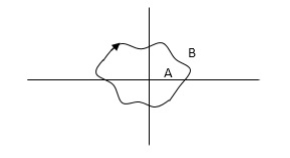
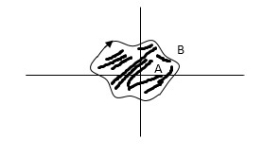
Encircled: A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption: -
|
|
Fig 6 Encirclement
In this example point A is encircled by the closed path Y. Since, a is inside the closed path point B is not encircled by y. it is outside the path. Furthermore, when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
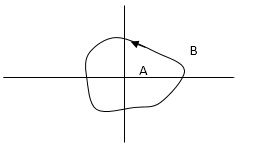
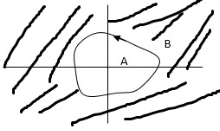
Enclosed: -
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region is
|
|
Fig 7 Enclosure
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. but is not enclosed by Y in fig b. and for point B it is vice versa.
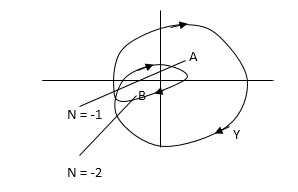
No of encirclements and enclosures:
For A line is cut once. For B line is cut twice
|
|
Fig 8 Encirclement and Enclosure with example
As it’s overlapping but 2 times in Same direction
When a point is encircled by a closed path Y, a no. N can be assigned to the no. of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘2 π N’.
For B = 2 = N for A = 1 = N
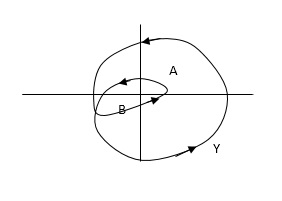
In this egg. point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians) all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1) |
|
Fig 9 Unity feedback control system
CLTF G(S)/1 + G(S) CE = 1 + G(S) = 1 + (S + Z1) (S + Z2)/ (S + P1) (S + P2) CE = (S + P1) (S + P2) + (S + Z1) (S + Z2)/ (S + P1) (S + P2) - - (2)
|
Key takeaways
- # OLTF poles is equal to CE poles.
- CE = (S + Z’1) (S + Z’2)/ (S + P1) (S + P2) - - (3)
- CLTF = G(S) – (1) / 1 + G(S) – (3)
= (S + Z1) (S + Z2) / (S + Z’1) (S + Z’2) - - (4)
4. # Zeros of characteristic equation is poles of CLTF (3 and 4).
5. For the closed loop system to be stable zeros of CE (i.e., poles of CLTF) should not be located at right half of the S-plane.
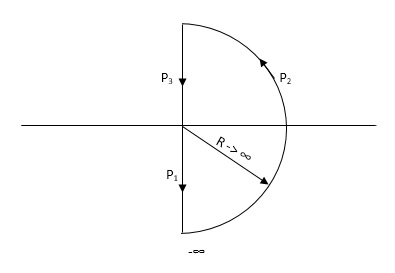
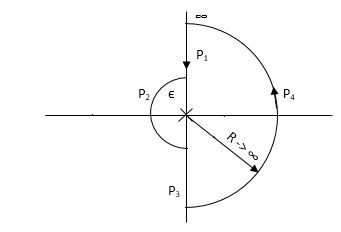
Consider a contour, which covers the entire right half of S-plane.
|
Fig 10 Contour for Right half of S-plane
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE: q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
- Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important: -
# Open loop System(stable): - When OL system is stable P=0 i.e. no of poles on right half N = Z – P If P = 0 N = Z
# Open loop system(unstable): -Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable. As N = Z – P N = Z – 1 For CL system to be stable the only criteria is (Z=0) i.e. N = -1 which means q(S) contour should encircle the origin one’s in CW direction.
|
Key takeaways
- When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
- The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
- The no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
|
Fig 11 Mapping
G(S) given then q(S) shift to right side.
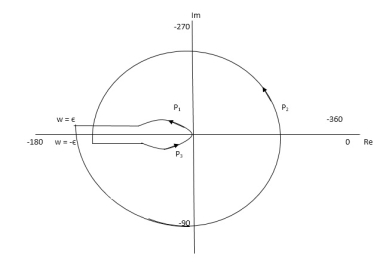
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1 Sol: - N = Z – P (No pole of right half of S Plane P = 0) P = 0, N = Z |
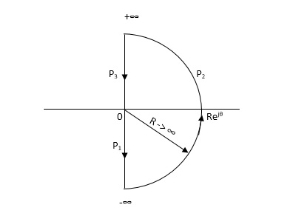
NYQUIST PATH: -
P1 = W – (0 to - ∞)
P2 = ϴ (- π/2 to 0 to π/2)
P3 = W (+∞ to 0)
|
Fig 12 Nyquist path
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
for P1: - W (0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2: -
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3: -
W = -∞ to 0
M = 1/√1+W2, φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 13
|
Fig 13 Nyquist Plot G(S) = 1/S+1
From plot we can see that -1 is not encircled so,
N = 0
But N = Z, Z = 0
So, system is stable.
Q.2. for the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/ (S + 4) (S + 5)
Soln: - N = Z – P, P = 0,
No pole on right half of S-plane
N = Z
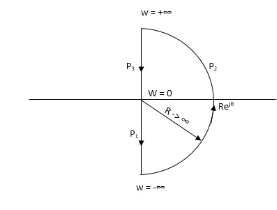
NYQUIST PATH
P1 = W (0 to -∞)
P2 = ϴ (-π/2 to 0 to +π/2)
P3 = W (∞ to 0)
|
Fig 14 Nyquist Path
Path P1 W (0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2: ϴ (-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/ (Rejϴ + 4) (Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 15. From plot N=0, Z=0, system stable.
|
Fig 15 Nyquist Plot G(S) = 1/ (S + 4) (S + 5)
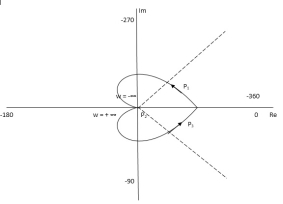
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1: Not including poles at origin in the Nyquist Path.
|
Fig 16 Nyquist Path
P1 W(∞ Ɛ) where Ɛ 0 P2 S = Ɛejϴ ϴ (+π/2 to 0 to -π/2) P3 W = -Ɛ to -∞ P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2 For P1 M = 1/w. w√102 + w2 = 1/w2√102 + w2 Φ = -1800 – tan-1(w/10) W M Φ ∞ 0 -3 π/2 Ɛ ∞ -1800 Path P3 will be mirror image of P1 about Real axis. G (Ɛ ejϴ) = 1/ (Ɛ ejϴ)2(Ɛ ejϴ + 10) Ɛ 0, ϴ = π/2 to 0 to -π/2 = 1/ Ɛ2 e2jϴ (Ɛ ejϴ + 10) = ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π] Path P2 will be formed by rotating through -π to 0 to +π Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2 G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ) = 0 N = Z – P No poles on right half of S plane so, P = 0 N = Z – 0 |
|
Fig 17 Nyquist Plot for G(S) = k/S2(S + 10)
But from plot shown in fig 16. it is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
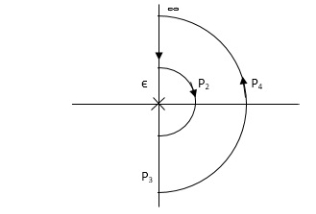
PART 2 Including poles at origin in the Nyquist Path.
|
Fig 18 Nyquist Path
P1 W(∞ to Ɛ) Ɛ 0 P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2) P3 W(-Ɛ to -∞) Ɛ 0 P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2) M = 1/W2√102 + W2, φ = - π – tan-1(W/10) P1 W (∞ to Ɛ) W M φ ∞ 0 -3 π/2 Ɛ ∞ -1800 P3(mirror image of P1) P2 S = Ɛejϴ G(Ɛejϴ) = 1/ Ɛ2e2jϴ (10 + Ɛejϴ) Ɛ 0 G(Ɛejϴ) = 1/ Ɛ2e2jϴ (10) = ∞. e-j2ϴϴ (π/2 to π to 3π/2) -2ϴ = (-π to -2π to -3π) P4 = 0 |
|
Fig 19 Nyquist Plot G(S) = k/S2(S + 10)
The plot is shown in fig 19. from the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path. (P = 2) [see path P2]
N = Z – P 0 = Z – 2 Z = 2 Hence, system is unstable. Path P2 will be formed by rotating through -π to -2π to -3π |
Key takeaways
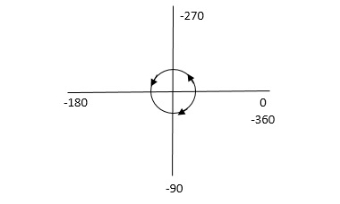
- The sign convention for angles is shown
|
Fig 20 Sign for Angle Directions
2. Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
References:
1. “Modern Control Engineering “, K. Ogata, Pearson Education Asia/
PHI, 4th Edition, 2002.
2. “Automatic Control Systems”, Benjamin C. Kuo, John Wiley India
Pvt. Ltd., 8th Edition, 2008.
3. “Feedback and Control System”, Joseph J Distefano III et al.,
Schaum’s Outlines, TMH, 2nd Edition 2007.
4. J. Nagarath and M. Gopal, “Control Systems Engineering”, New Age
International (P) Limited, Publishers, Fourth edition – 2005