UNIT 3
Projection of Solids
A solid has three dimensions, viz. Length, breadth and thickness. To represent a solid on a flat surface having only length and breadth, at least two orthographic views are necessary. Sometimes, additional views projected on auxiliary planes become necessary to make the description of a solid complete.
This chapter deals with the following topics:
1. Types of solids.
2. Projections of solids in simple positions.
(a) Axis perpendicular to the H.P.
(b) Axis perpendicular to the V.P.
(c) Axis parallel to both the H.P. And the V.P.
3. Projections of solids with axes inclined to one of the reference planes and
Parallel to the other.
(a) Axis inclined to the V.P. And parallel to the H.P.
(b) Axis inclined to the H.P. And parallel to the V.P.
4. Projections of solids with axes inclined to both the H.P. And the V.P.
5. Projections of spheres.
Solids may be divided into two main groups:
(1) Polyhedra
(2) Solids of revolution.
Polyhedra: A polyhedron is defined as a solid bounded by planes called faces. When all faces are equal and regular, the polyhedron is said to be regular. There are seven regular polyhedra which may be defined as stated below:
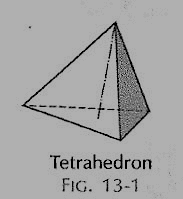
(i) Tetrahedron (fig. 1): It has four equal faces, each an equilateral triangle.
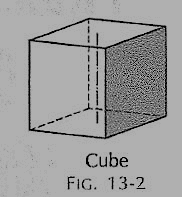
(ii) Cube or hexahedron (fig. 2): It has six faces, all equal squares.
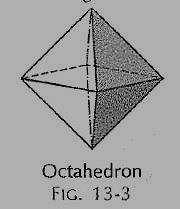
(iii) Octahedron (fig. 3): It has eight equal equilateral triangles as faces.
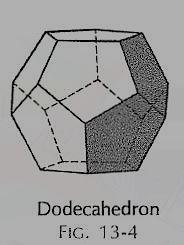
(iv) Dodecahedron (fig. 4): It has twelve equal and regular pentagons as faces.
(v) Icosahedron (fig. 5): It has twenty faces, all equal equilateral triangles.
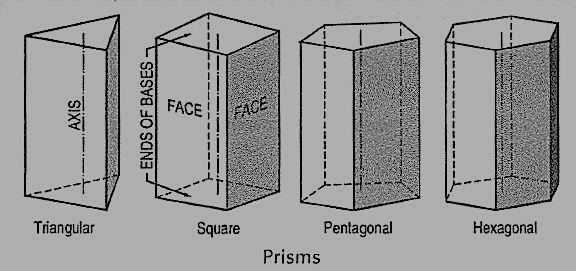
(vi) Prism: This is a polyhedron having two equal and similar faces called its ends or bases, parallel to each other and joined by other faces which are parallelograms. The imaginary line joining the centres of the bases is called the axis. A right and regular prism (fig. 6) has its axis perpendicular to the bases. All its faces are equal rectangles.
(vii) Pyramid: This is a polyhedron having a plane figure as a base and many triangular faces meeting at a point called the vertex or apex. The imaginary line joining the apex with the centre of the base is its axis.
A right and regular pyramid (fig. 7) has its axis perpendicular to the base which is a regular plane figure. Its faces are all equal isosceles triangles.
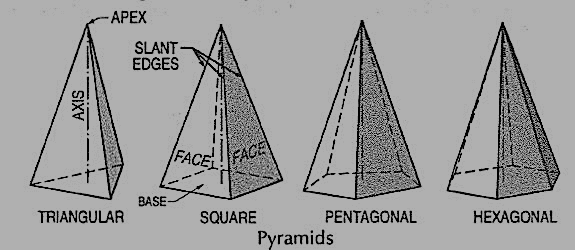
Oblique prisms and pyramids have their axes inclined to their bases. Prisms and pyramids are named according to the shape of their bases, as triangular, square, pentagonal, hexagonal etc.
4.1 Solids of revolution
(i) Cylinder (fig. 8): A right circular cylinder is a solid generated by the revolution of a rectangle about one of its sides which remains fixed. It has two equal circular bases. The line joining the centres of the bases is the axis. It is perpendicular to the bases.
(ii) Cone (fig. 9): A right circular cone is a solid generated by the revolution of a right-angled triangle about one of its perpendicular sides which is fixed.
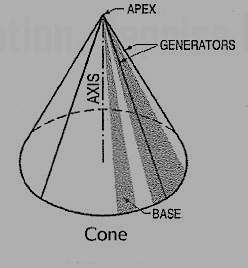
It has one circular base. Its axis joins the apex with the centre of the base to which it is perpendicular. Straight lines drawn from the apex to the circumference of the base-circle are all equal and are called generators of the cone. The length of the generator is the slant height of the cone.
(iii) Sphere (fig. 10): A sphere is a solid generated by the revolution of a semi-circle about its diameter as the axis. The mid-point of the diameter is the centre of the sphere. All points on the surface of the sphere are equidistant from its centre.

(iv) Frustum: When a pyramid or a cone is cut by a plane parallel to its base, thus removing the top portion, the remaining portion is called its frustum (fig. 11).
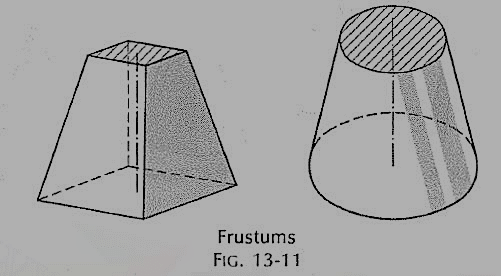
(v) Truncated: When a solid is cut by a plane inclined to the base it is said to be truncated.
Projections of solids in simple positions
A solid in simple position may have its axis perpendicular to one reference plane or parallel to both. When the axis is perpendicular to one reference plane, it is parallel to the other. Also, when the axis of a solid is perpendicular to a plane, its base will be parallel to that plane. When a plane is parallel to a reference plane, its projection on that plane shows its true shape and size.
Therefore, the projection of a solid on the plane to which its axis is perpendicular, will show the true shape and size of its base.
Hence, when the axis is perpendicular to the ground, i.e. to the H.P., the top view should be drawn first, and the front view projected from it.
When the axis is perpendicular to the V.P., beginning should be made with the front view. The top view should then be projected from it.
When the axis is parallel to both the H.P. And the V.P., neither the top view nor the front view will show the actual shape of the base. In this case, the projection of the solid on an auxiliary plane perpendicular to both the planes, viz. The side view must be drawn first. The front view and the top view are then projected from the side view. The projections in such cases may also be drawn in two stages.
Problems:
Axis perpendicular to the H.P.:
Problems:
1. Draw the projections of a triangular prism, base 40 mm side and axis 50 mm long, resting on one of its bases on the H.P. With a vertical face perpendicular to the V.P.
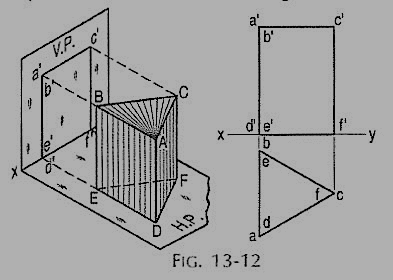
(i) As the axis is perpendicular to the ground i.e. the H.P. Begin with the top view. It will be an equilateral triangle of sides 40 mm long, with one of its sides perpendicular to xy. Name the corners as shown, thus completing the top view. The corners d, e and fare hidden and coincide with the top corners a, b and c respectively
(ii) Project the front view, which will be a rectangle. Name the corners. The line b'e' coincides with a'd'.
2. Draw the projections of a pentagonal pyramid, base 30 mm edge and axis 50 mm long, having its base on the H.P. And an edge of the base parallel to the V.P. Also draw its side view.
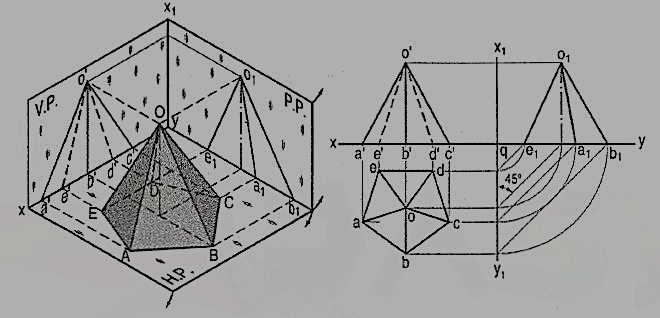
(i) Assume the side DE which is nearer the V.P., to be parallel to the V.P. As shown in the pictorial view.
(ii) In the top view, draw a regular pentagon abcde with ed parallel to and nearer xy. Locate its centre o and join it with the corners to indicate the slant edges.
(iii) Through o, project the axis in the front view and mark the apex o', 50 mm above xy. Project all the corners of the base on xy. Draw lines o'a', o'b' and o'c' to show the visible edges. Show o'd' and o'e' for the hidden edges as dashed lines.
(iv) For the side view looking from the left, draw a new reference line x1y1 perpendicular to xy and to the right of the front view. Project the side view on it, horizontally from the front view as shown. The respective distances of all the points in the side view from x1y1, should be equal to their distances in the top view from xy. This is done systematically as explained below:
(v) From each point in the top view, draw horizontal lines up to x1y1. Then draw lines inclined at 45° to x1y1 (or xy) as shown. Or, with q, the point of intersection between xy and x1y1 as centre, draw quarter circles. Project up all the points to intersect the corresponding horizontal lines from the front view and complete the side view as shown in the figure. Lines o1d1 and o1c1 coincide with o1e1 and o1a1 respectively.
Axis perpendicular to the V.P.:
A hexagonal prism (fig. 14) has one of its rectangular faces parallel to the H.P. Its axis is perpendicular to the V.P. And 3.5 cm above the ground. Draw its projections when the nearer end is 2 cm in front of the V.P. Side of base 2.5 cm long; axis 5 cm long.

(i) Begin with the front view. Construct a regular hexagon of 2.5 cm long sides with its centre 3.5 cm above xy and one side parallel to it.
(ii) Project down the top view, keeping the line for nearer end, viz. 1-4, 2 cm below xy.
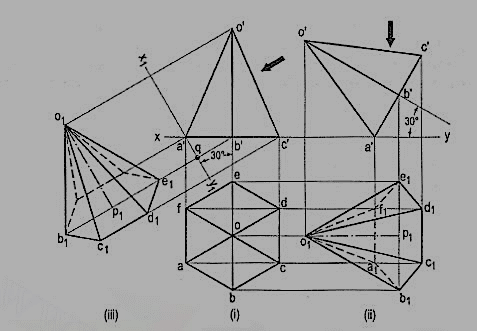
2. A square pyramid fig. 15, base 40 mm side and axis 65 mm long, has its base in the V.P. One edge of the base is inclined at 30° to the H.P. And a corner contained by that edge is on the H.P. Draw its projections.
(i) Draw a square in the front view with the corner d' in xy and the side d'c' inclined at 30° to it. Locate the centre o' and join it with the corners of the square.
(ii) Project down all the corners in xy (because the base is in the V.P.). Mark the apex o on a projector through o'. Draw lines for the slant edges and complete the top view.
Axis parallel to both H.P. And the V.P.
A triangular prism1 base 40 mm side and height 65 mm is resting on the H.P. On one of its rectangular faces with the axis parallel to the V.P. Draw its projections.
As the axis is parallel to both the planes, begin with the side view.
(i) Draw an equilateral triangle representing the side view, with one side in xy.
(ii) Project the front view horizontally from this triangle.
(iii) Project down the top view from the front view and the side view, as shown.

Problems:
Draw the projections of the following solids, situated in their respective positions, taking a side of the base 40 mm long or the diameter of the base 50 mm long and the axis 65 mm long.
1. A hexagonal pyramid, base on the H.P. And a side of the base parallel to and 25 mm in front of the V.P.
2. A square prism, base on the H.P., a side of the base inclined at 30° to the V.P. And the axis 50 mm in front of the V.P.
3. A triangular pyramid, base on the H.P. And an edge of the base inclined at 45° to the V.P.; the apex 40 mm in front of the V.P.
Projections of solids with axis inclined to one of the reference planes and parallel to the other:
When a solid has its axis inclined to one plane and parallel to the other, its projections are drawn in two stages.
(1) In the initial stage, the solid is assumed to be in simple position, i.e. its axis perpendicular to one of the planes.
If the axis is to be inclined to the ground, i.e. the H.P., it is assumed to be perpendicular to the H.P. In the initial stage. Similarly, if the axis is to be inclined to the V.P., it is kept perpendicular to the V.P. In the initial stage.
Moreover
(i) if the solid has an edge of its base parallel to the H.P. Or in the H.P. Or on the ground, that edge should be kept perpendicular to the V.P.; if the edge of the base is parallel to the V.P. Or in the V.P., it should be kept perpendicular to the H.P.
(ii) If the solid has a corner of its base in the H.P. Or on the ground, the sides of the base containing that corner should be kept equally inclined to the V.P.; if the corner is in the V.P., they should be kept equally inclined to the H.P.
Axis inclined to the VP and parallel to the HP:
1. Draw the projections of a pentagonal prism, base 25 mm side and axis 50 mm long, resting on one of its faces on the H.P., with the axis inclined at 45° to the V.P.
In the simple position, assume the prism to be on one of its faces on the ground with the axis perpendicular to the V.P.
Draw the pentagon in the front view with one side in xy and project the top view [fig. 17].
The shape and size of the figure in the top view will not change, so long as the prism has its face on the H.P. The respective distances of all the corners in the front view from xy will also remain constant.

Method I: [fig. 17 (i)]:
(i) Alter the position of the top view, i.e. reproduce it so that the axis is inclined at 45° to xy. Project all the points upwards from this top view and horizontally from the first front view, e.g. a vertical from a intersecting a horizontal from a' at a point a'1.
(ii) Complete the pentagon a'1b'1c'1d'1e'1 for the fully visible end of the prism. Next, draw the lines for the longer edges and finally, draw the lines for the edges of the other end. Note carefully that the lines a'1 1'1, 1'12'1 and 1'15'1 are dashed lines. e'1 5'1 is also hidden but it coincides with other visible lines.
Method II: [fig. 17(ii)]:
(i) Draw a new reference line x1y1, making 45° angle with the top view of the axis, to represent an auxiliary vertical plane.
(ii) Draw projectors from all the points in the top view perpendicular to x1y1 and on them, mark points keeping the distance of each point from x1y1 equal to its distance from xy in the front view. Join the points as already explained. The auxiliary front view and the top view are the required projections.
Axis inclined to the H.P. And parallel to the V.P.
Problems:
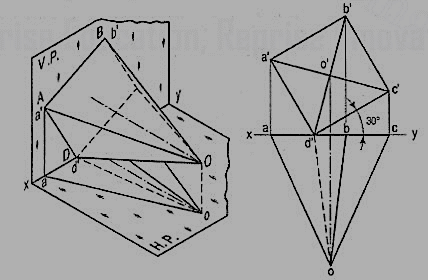
1. A hexagonal pyramid, base 25 mm side and axis 50 mm long, has an edge of its base on the ground. Its axis is inclined at 30° to the ground and parallel to the V.P. Draw its projections. In the initial position assume the axis to be perpendicular to the H.P.
Draw the projections with the base in xy and its one edge perpendicular to the V.P. Fig. 18 (i)
If the pyramid is now tilted about the edge AF (or CD) the axis will become inclined to the H.P. But will remain parallel to the V.P. The distances of all the corners from the V.P. Will remain constant.
The front view will not be affected except in its position in relation to xy. The new top view will have its corners at same distances from xy, as before.
Method I: [fig. 18 (ii)]:
(i) Reproduce the front view so that the axis makes 30° angle with xy and the point a' remains in xy.
(ii) Project all the points vertically from this front view and horizontally from the first top view. Complete the new top view by drawing (a) lines joining the apex o'1 with the corners of the base and (b) lines for the edges of the base.
The base will be partly hidden as shown by dashed line a1b1, e1f1 and f1a1. Similarly, o1f1 and o1a1 are also dashed lines.
Method II: [fig. 18(iii)]:
(i) Through a' draw a new reference line x1y1 inclined at 30° to the axis, to represent an auxiliary inclined plane.
(ii) From the front view project, the required top view on x1y1, keeping the distance of each point from x1y1 equal to the distance of its first top view from xy, viz. e1q = eb' etc.
2. Draw the projections of a cone, base 75 mm diameter and axis 100 mm long, lying on the H.P. On one of its generators with the axis parallel to the V.P.
(i) Assuming the cone to be resting on its base on the ground, draw its projections.
(ii) Re-draw the front view so that the line o'7' (or o'1 ') is in xy. Project the required top view as shown. The lines from o1 should be tangents to the ellipse.
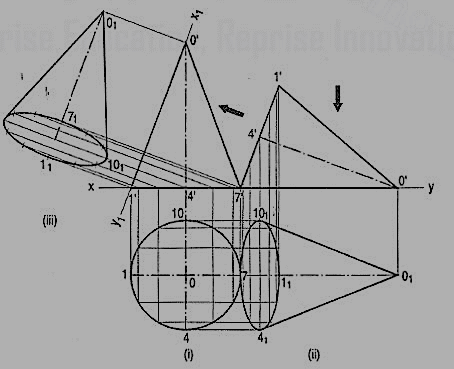
The top view obtained by auxiliary-plane method is shown in fig. 13-24(ii). The new reference line x1y1 is so drawn as to contain the generator o'1' instead of o'7' (for sake of convenience). The cone is thus lying on the generator o'1 '. Note that 1 '1 1 = 1 '1, o'o1 = 4'o etc. Also note that the base is fully visible in both the methods.
Projections of the solids with axis inclined to both the H.P. And the V.P.
The projections of a solid with its axis inclined to both the planes are drawn in three stages:
(i) Simple position
(ii) Axis inclined to one plane and parallel to the other
(iii) Final position.
The second and final positions may be obtained either by the alteration of the positions of the solid, i.e. the views, or by the alteration of reference lines.
Problem:
1. A square prism, base 40 mm side and height 65 mm, has its axis inclined at 45° to the H.P. And has an edge of its base, on the H.P and inclined at 30° to the V.P. Draw its projections.
Method I: Fig. 20
i) Assuming the prism to be resting on its base on the ground with an edge of the base perpendicular to the V.P., draw its projections. Assume the prism to be tilted about the edge which is perpendicular to the V.P., so that the axis makes 45° angle with the H.P.
(ii) Hence, change the position of the front view so that the axis is inclined at 45° to xy and f' (or e') is in xy. Project the second top view. Again, assume the prism to be turned so that the edge on which it rests, makes an angle of 30° with the V.P., keeping the inclination of the axis with the ground constant. The shape and size of the second top view will remain the same; only its position will change. In the front view, the distances of all the corners from xy will remain the same as in the second front view.
(iii) Therefore, reproduce the second top view making f1g1 inclined at 30° to xy. Project the final front view upwards from this top view and horizontally from the second front view, e.g. a vertical from a1 and a horizontal from a' intersecting at a'1. As the top end is further away from xy in the top view it will be fully visible in the front view. Complete the front view showing the hidden edges by dashed lines.
(iv) The second top view may be turned in the opposite direction as shown. In this position, the lower end of the prism, viz. e'lf'1g'1h'1 will be fully visible in the front view.

Method II: Fig. 21
(i) Draw the top view and front view in simple position.
(ii) Through f', draw a new reference line x1y1 making 45° angle with the axis. On it, project the auxiliary top view.
(iii) Draw another reference line x2y2 inclined at 30° to the line fig 1. From the auxiliary top view, project the required front view, keeping the distance of each point from x2y2, equal to its distance (in the first front view) from x1y1 i.e. a'1q1 = a'q etc