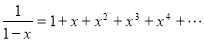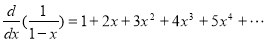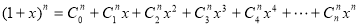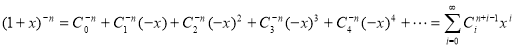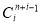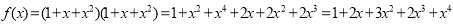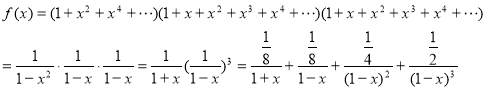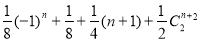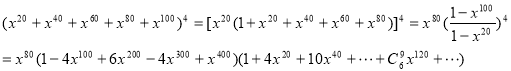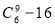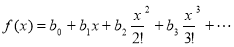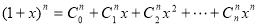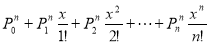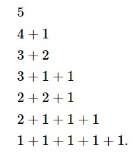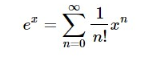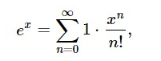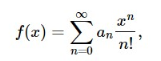UNIT – 7
Generating Functions
f(x)=a0+a1x+a2x2+a3x3+…. is the general generating function of a series: a0, a1, a2, a3, …. Example 1.
Example 2.
Example 3.
Example 4.
|
Example 1. There are 2 A’s and 2 B’s. (a) In how many ways of combinations can we select 2 letters from A’s, and B’s? (b)In how many ways can we select 3 letters from A’s, and B’s? (a) AA, AB or BA, BB: 3 ways. (b) AAB or BAA or ABA, BBA or BAB or ABB: 2 ways Utilizing the general generating function:
Example 2. There are infinite A’s, B’s, and C’s. In how many ways can we select n letters from A’s, B’s, and C’s, with even numbers of A’s?
an= Example. There are 200 identical chairs. In how many ways can we place 4 rooms to have 20, or 40, or 60, or 80, or 100 chairs in each room? a200= |
Example. |
A partition of a positive integer n, also called an integer partition, is a method of writing n as a sum of positive integers in number theory and combinatorics. The same partition is known to be two sums, which differ only in the order of their sums. (The sum becomes a composition, if order matters.)
The partitions of 5 are
|
Thus p5=7.
There are other ways that a function might be said to generate a sequence, other than as what we have called a generating function. For example,
is the generating function for the sequence 1,1,12,13!,…1,1,12,13!,…. But if we write the sum as
considering the n!n! to be part of the expression xn/n!xn/n!, we might think of this same function as generating the sequence 1,1,1,…1,1,1,…, interpreting 1 as the coefficient of xn/n!xn/n!. This is not a very interesting sequence, of course, but this idea can often prove fruitful. If
we say that f(x)f(x) is the exponential generating function for a0, a1, a2, … |
|
7.6.1 Operands
v is a vector.
i is the name of range variable.
j is the name of a local range variable.
X is an expression that typically contains i or j and that evaluates to a real number.
m, n are real numbers. n > m.
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.