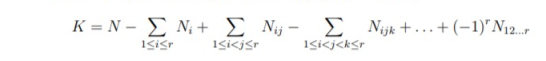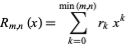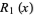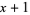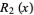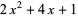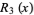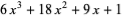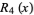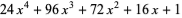UNIT – 6
The Principle of Inclusion and Exclusion
The Principal of Inclusion and Exclusion (PIE) theory is a counting technique which calculates the number of elements fulfilling at least one of several properties, while ensuring that elements satisfying more than one property are not counted twice.
6.1.1 Generalised PIE
Often the following theorem is called either the cross-classification theory, or
or the principle of inclusion-exclusion. We are enunciating the principle now.
Let S be a set of N distinct elements, and let S1, . . . , Sr be arbitrary subsets of S containing N1, . . . , Nr elements, respectively. For 1 ≤ i < j < . . . < l ≤ r, let Sij...l be the intersection of Si , Sj , . . . , Sl and let Nij...l be the number of elements of Sij...l. Then the number K of elements of S not in any of S1, . . . , Sr is
|
A Derangement is a permutation of n elements, so that in its original position, no element exists. For example, {0, 1, 2, 3} is a {2, 3, 1, 0} derangement. Find the total number of derangements of a group of n elements, given the number n. Example 1 Input: n = 2 Output: 1 For two elements say {0, 1}, there is only one possible derangement {1, 0}
Example 2 Input: n = 3 Output: 2 For three elements say {0, 1, 2}, there are two possible derangements {2, 0, 1} and {1, 2, 0}
Example 3 Input: n = 4 Output: 9 For four elements say {0, 1, 2, 3}, there are 9 possible derangements {1, 0, 3, 2} {1, 2, 3, 0} {1, 3, 0, 2}, {2, 3, 0, 1}, {2, 0, 3, 1}, {2, 3, 1, 0}, {3, 0, 1, 2}, {3, 2, 0, 1} and {3, 2, 1, 0} |
A rook polynomial is a generating polynomial in combinatorial mathematics for the number of ways to place non-attacking rooks on a board that looks like a checkerboard; that is, there may be no two rooks in the same row or column.
A rook polynomial is a polynomial
whose number of ways
where The first few rook polynomials
|
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.