Unit-3
Trees
In diagram hypothesis, a tree is an undirected, associated, and non-cyclic chart. As such, an associated chart that doesn't contain even a solitary cycle is known as a tree.
A tree addresses the various levelled structure in a graphical structure.
The components of trees are called their hubs and the edges of the tree are called branches.
A tree with n vertices has (n-1) edges.
Trees give numerous helpful applications as straightforward as a genealogical record to as perplexing as trees in information constructions of software engineering.
A leaf in a tree is a vertex of degree 1 or any vertex having no kids is known as a leaf.
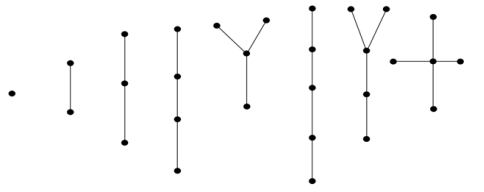
Example 1:
|
Figure 1
In the above example, all are trees with fewer than 6 vertices.
In diagram hypothesis, a wood is an undirected, disengaged, non-cyclic chart. All in all, a disjoint assortment of trees is known as timberland. Every segment of a woodland is tree.
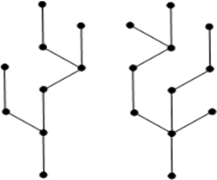
Example:
|
Figure 2
The above diagram seems as though two sub-graphs yet it is a solitary disengaged diagram. There are no cycles in the above chart. Hence it is a forest.
Each tree which has in any event two vertices ought to have at any rate two leaves.
Trees have numerous portrayals:
Let T alone a diagram with n vertices, at that point the accompanying assertions are same:
- T is a tree.
- T contains no cycles and has n-1 edges.
- T is associated and has (n - 1) edge.
- T is associated diagram, and each edge is a cut-edge.
- Any two vertices of diagram T are associated by precisely one way.
- T contains no cycles, and for any new edge e, the diagram T+ e has precisely one cycle.
Each edge of a tree is cut - edge.
Adding one edge to a tree characterizes precisely one cycle.
Each associated diagram contains a spreading over tree.
Each tree has at any rate two vertices of degree two.
An established tree is a tree with an extraordinary vertex marked as the "root" the of the tree.
The root fills in as a perspective for other vertices in the tree. In charts, we normally keep the root at the top and rundown other vertices beneath it.
This idea is especially helpful in software engineering for working with tree-based information structures.
In the figure, the root vertex is appeared with a dark boundary.
The following are some helpful terms related with established trees.
The branch is simply one more name given to the edges of the tree.
The Depth or profundity of a vertex is the quantity of branches in the way from the root to the vertex. So the profundity of the actual root is zero.
The level of a vertex is some of a vertex in the way from the root to the vertex. This is only one more than the profundity of the vertex. The level of the root is 1.
A leaf is a vertex with no youngster.
Height of tree is the most extreme estimation of depth or profundity for any vertex in the tree.
|
Figure 3
3.6.1 Binary Tree
A binary tree is a tree information structure in which every hub has all things considered two kid hubs. The kid hubs are known as the left kid and right kid.
A paired tree might have various sorts: established, full, total, awesome, adjusted, or degenerate.
The delineation shows a total parallel tree, which has each level totally filled, however with a potential exemption for the last level:
|
Figure 4
Parallel trees have two regular portrayals:
- Array: fills the exhibit in a top-down methodology, from left to directly in each level, and an unfilled space for any missing youngster
- Linked list: addresses hub object by hub information, left pointer, and right pointer
3.6.2 Binary Search Tree (BST)
Binary Search Tree, Binary Sorted Tree or BST, may be a binary tree satisfies the subsequent condition:
- For each node, the left sub-tree contains only nodes with values but that node’s value
- For each node, the proper sub-tree contains only nodes with values greater than that node’s value
- Left and right sub-trees are also BSTs
The illustration shows a binary search tree of size 9 and depth 3:
|
Figure 5
BST keeps the keys in sorted order so that searching for a key or finding a place to insert a key is done in O(n) in the worst case, and O(log n) in the average case, where n is a tree size.
3.6.3 Tree Sort
Tree sorting is an online sorting algorithm that generates a binary search tree from the input elements to be sorted and then moves through the tree in sequence, so that the elements are sorted out in order.
Let's look at what the measures are:
- Gets the feedback of elements in an array
- Build a binary search tree by adding the array's data items into the tree.
- Performs in-order crossing on the tree in order to get the components in sorted order
So, we'll use the binary tree's array representation as an input to work it out.
3.6.4 Pseudocode
Since the first step is very simple, we present step two and step three pseudocodes.
The function continues recursively searching for the correct location for the input variable for the second step of the algorithm by comparing it to the root of each subtree. The following pseudocode shows the specifics of that function, Insert(Node node, Key value):
|
For the third step, the function goes through all the tree recursively to get the left side of each subtree printed before the right side. This guarantees to print the tree in order. The following pseudocode, traverseInOrder(Node node) shows the details of that function:
|
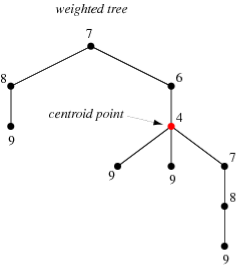
A tree to whose hubs or potentially edges marks (generally number) are appointed.
|
Figure 6
"Weight" likewise has a more explicit significance when applied to trees, to be specific the heaviness of a tree at a point u is the greatest number of edges in any branch at u, as delineated previously. A point having negligible load for the tree is known as a centroid point, and the tree centroid is the arrangement of all centroid focuses.
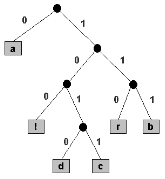
Most easily, a prefix code is represented by a binary tree where external nodes are marked with single characters that are combined to form a message. The character encoding is defined by following the direction down from the tree root to the external node carrying the character: a 0 bit identifies the path to the left branch and a 1 bit identifies the path to the right branch. The black circles in the above tree are internal nodes, and the gray squares are external nodes. The code for b is 111, since, by taking 3 consecutive right branches, the external node carrying b is reached from the root. In the table below, the other codes are given.
|
Figure 7
Note that each character has a (potentially) separate number of bits encoded on it. The character 'a' is encoded with a single bit in the case above, while the character 'd' is encoded with 4 bits. This is a basic property of codes for prefixes. We use short encodings for commonly used characters, and long encodings for uncommon ones, in order for this encoding scheme to decrease the number of bits in a letter.
A second fundamental property of prefix codes is that by merely stringing together the code bits from left to right, messages can be generated. For instance, the bit string
0111110010110101001111100100 encodes the message "abracadabra!". The first 0 must encode 'a', then the next three 1's must encode 'b', then 110 must encode r, and so on as follows: |0|111|110|0|1011|0|1010|0|111|110|0|100 a b r a c a d a b r a ! |
The codes can be run together because no encoding is a prefix of another one. This property defines a prefix code, and it allows us to represent the character encodings with a binary tree, as shown above. To decode a given bit string:
- Start at the root of the tree.
- Repeat until you reach an external leaf node.
- Read one message bit.
- Take the left branch in the tree if the bit is 0; take the right branch if it is 1.
- Print the character in that external node.
This whole process is repeated, starting over at the root, until all of the bits in the compressed message are exhausted. Your main task is to read in the binary tree and implement this procedure.
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.