Unit-2

Introduction to Graph Theory contd

2.1 Planar Graph

"A diagram is supposed to be planar if it very well may be drawn on a plane with no edges crossing. Such a drawing is known as a planar portrayal of the graph."

A chart might be planar regardless of whether it is drawn with intersections, since it very well might be conceivable to attract it an alternate route without intersections.

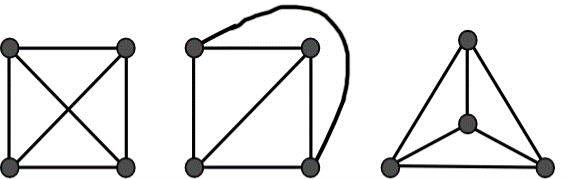
For instance, consider the total chart K_{4} and its two potential planar portrayals –

Figure 1

2.1.1 Regions in Planar Graphs –

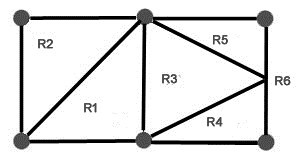
The planar portrayal of a diagram parts the plane into areas. These locales are limited by the edges with the exception of one district that is unbounded. For instance, think about the accompanying chart "

Figure 2

There are a sum of 6 regions with 5 limited regions and 1 unbounded area R{6}.

2.2 Hamiltonian Path and Cycle

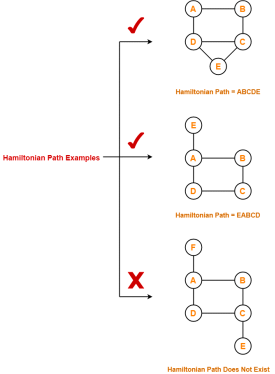
A cycle that utilizes each vertex in a graph precisely whenever is known as a Hamilton cycle, and a way that utilizes each vertex in a diagram precisely whenever is known as a Hamilton path.

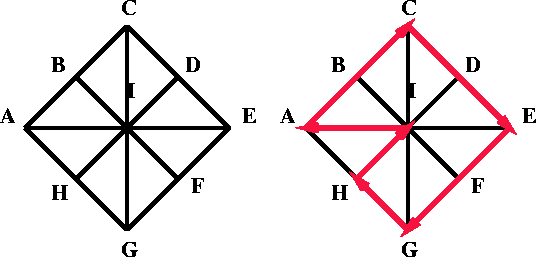
Figure 3

(1)                                                                                    (2)

Hamiltonian cycle shown in graph (2) with Red marking

2.3 Graph Colouring

Diagram shading is the methodology of task of tones to every vertex of a chart G with the end goal that no adjoining vertices get same tone. The goal is to limit the quantity of shadings while shading a chart. The most modest number of tones needed to shading a diagram G is called its chromatic number of that chart. Diagram shading issue is a NP Complete issue.

2.3.1 Technique to Colour a Graph

The means needed to shading a diagram G with n number of vertices are as per the following −

Stage 1 − Arrange the vertices of the chart in some request.

Stage 2 − Choose the main vertex and shading it with the principal tone.

Stage 3 − Choose the following vertex and shading it with the most reduced numbered shading that has not been hued on any vertices neighboring it. In the event that all the contiguous vertices are hued with this tone, dole out another tone to it. Rehash this progression until all the vertices are shaded.

Figure 4

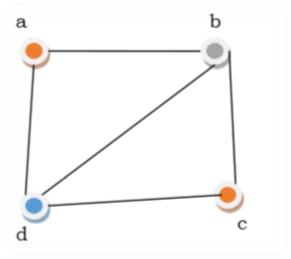
In the above figure, from the start vertex an is shaded red. As the contiguous vertices of vertex an are again neighbouring, vertex b and vertex d are shaded with various tone, green and blue individually. At that point vertex c is hued however red as no adjoining vertex of c may be hued red. Consequently, we could colouring the chart by 3 tones. Consequently, the chromatic number of the chart is 3.

2.4 Chromatic Polynomial

For a given diagram G, the quantity of methods of shading the vertices with x or less tones is signified by P(G, x) and is known as the chromatic polynomial of G (regarding x).

Example 1:

References

1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.

2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.

3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.

4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.